Na počátku tisíciletí vybral americký Clay Institute sedm důležitých matematických problémů a na vyřešení každého z nich vypsal odměnu ve výši milion dolarů. Jeden z nich se zabývá komplexními kořeny Riemannovy funkce zeta.

Riemannova hypotéza patří k nejdůležitějším nevyřešeným problémům současné matematiky a plným právem jí náleží čestné místo mezi zmíněnou sedmičkou tisíciletí. Jak už název napovídá, domněnku poprvé vyslovil německý matematik Bernhard Riemann ve svém článku „O počtu prvočísel menších než daná hodnota“ (Über die Anzahl der Primzahlen unter einer gegebenen Größe), který publikoval v roce 1859. V něm uvedl do praxe jeden z nejmocnějších nástrojů analytické teorie čísel - rozšíření zeta funkce do komplexního oboru.

A právě rozložení kořenů této funkce v komplexní rovině se dotýká hypotéza, na jejíž hlavu je vypsána ona milionová odměna. Můžete si ji tedy představit jako pokus vyřešit kvadratickou rovnici s komplexními kořeny, řekněme,

z^2 - 3z + 7 = 0

pouze s tím „drobným“ rozdílem, že na levé straně nebudete mít kvadratickou funkci, ale zeta funkci. Budete tedy analyzovat všechna řešení rovnice Zeta(z) = 0 v komplexní rovině. A dokonce je ani nebudete muset všechny najít (ono je jich taky nekonečně mnoho). Stačí, když ukážete, že všechny netriviální kořeny leží v komplexní rovině na vertikální přímce x = 1/2.

A protože je mi jasný, že se na ty prachy přímo třesete, nebudeme dělat žádné skopičiny a jdeme rovnou na věc.

Komplexní funkce zeta

(jako obvykle: 2*3 bude „dva krát tři“ a 2^3 bude „dvě na třetí“)

Funkci zeta - zatím jen s reálnou proměnnou s - navrhnul v první polovině 18. století Leonard Euler jako pomůcku pro studium vlastností celých čísel, zejména prvočísel. Zeta funkce se totiž dá rozepsat jako tzv. Eulerův součin), do kterého každé prvočíslo přispívá jedním faktorem. Nekonečný součin je ale konceptuálně komplikovanější než součet, a proto se hodnota funkce zeta(s) pro dané reálné číslo s obvykle definuje pomocí nekonečné řady zadané formulkou (1).

(ostatní formulky zatím ignorujte - k nim se dostanu v průběhu článku)

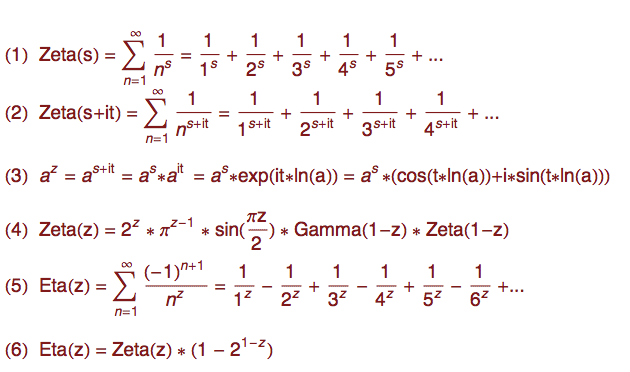
Nekonečná řada čísel nemusí mít nutně konečný součet. Standardní analýzou konvergence - přesně tou, se kterou se dnes potýkají studenti technických oborů v prváku - se ukázalo, že důležitou hranicí pro konečnost naznačeného součtu je hodnota s=1, která vede k tzv. harmonické řadě):

1 + 1/2 + 1/3 + 1/4 + 1/5 + ...

Když si členy začnete zkusmo sčítat, zjistíte, že průběžný součet roste sice velmi pomalu, ale nakonec se do nekonečna přece jen doplazí, takže hodnota zeta(1) bude nekonečno (říkáme, že zeta funkce má pól v bodě s=1).

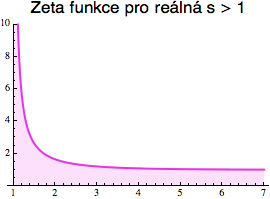
Pro všechna s>1 se členy napravo již zmenšují dostatečně rychle, takže řada konverguje a její konečný součet pak definuje hodnotu zeta(s). Pro s<1 řada diverguje (součet je nekonečný) a pro tato s není reálná zeta funkce definována. Její chování na definičním intervalu je zobrazeno na obrázku vpravo (můžete si sami zkusit, že pro velké hodnoty s se členy ve formulce (1) vpravo zmenšují tak rychle, že celá suma je pak jen těsně nad jedničkou).

Z pohledu reálné analýzy by se s trochou nadsázky dalo říci, že zeta patří k nejnudnějším funkcím celé matematiky. Žádné extrémy, žádný přechod z konvexního režimu do konkávního, žádné kořeny.

Tento pohled se však zásadně změnil v okamžiku, kdy Riemanna napadlo tuto funkci rozšířit do komplexní roviny. V ní se z ošklivého káčátka vyklubala elegantní (byť trochu mystická) labuť.

Definice komplexní zeta funkce (2) je prakticky stejná jako v reálném případě, jen si za exponenty příslušné řady volíme komplexní čísla (v případě zeta funkce se pro komplexní proměnnou zpravidla používá notace z = s+it namísto klasického z=x+iy).

+++++++++

Nejprve si musíme říci, jak umocnit reálné číslo na komplexní exponent.

Není to žádná velká věda - v podstatě se odvoláme na středoškolskou definici obecné mocniny pomocí exponenciely a logaritmu:

a^z = exp(z*ln(a))

Díky tomu, že všechny základy ve formulce (2) jsou reálná čísla, logaritmus na pravé straně je reálný (přirozený) a nemusíme si lámat hlavu se záludnostmi komplexního logaritmu. Budeme však potřebovat komplexní exponenciálu (viz starší Matykání), která nám umožní definovat žádanou komplexní mocninu pomocí formulky (3). První část výsledné hodnoty vpravo ukazuje absolutní hodnotu mocniny, zatímco ta druhá udává „směr“ komplexního čísla (celá ta věc v závorce napravo je vlastně bod na jednotkové kružnici a tedy jakýsi směrový vektor). Použití této formulky si můžete sami procvičit:

(1/2)^(2+3i) = (0.5)^(2+3i) = -0.1217 - 0.2184 i

(1/4)^(2.3-3.7i) = (0.25)^(2.3-3.7i) = 0.0167 - 0.0377 i

Jak nekonečná suma funguje (v reálném i komplexním případě), si můžeme znázornit geometricky. Každý člen řady v definiční formulce si představíme jako malou úsečku (či vektor), liché členy modře, sudé žlutě, a výsledný součet dostaneme tak, že úsečky zřetězíme - tedy postavíme jednu za druhou (nezapomeňte, že komplexní čísla sčítáme jako vektory)- a podíváme se, kam se takto vzniklý dvoubarevný had po nekonečně mnoha krocích doplazí.

Pro reálnou funkci zeta je to ukázáno na následujícím obrázku vlevo (s=1.75), pro komplexní pak vpravo (z = 1.75-2i). Například druhý sčítanec komplexního součtu (2) pak odpovídá výrazu (1/2)^(1.75-2i), což se po vyčíslení rovná 0.0545+0.292i, a proto druhá (žlutá) úsečka vpravo trčí ve směru severo-severo-východním.

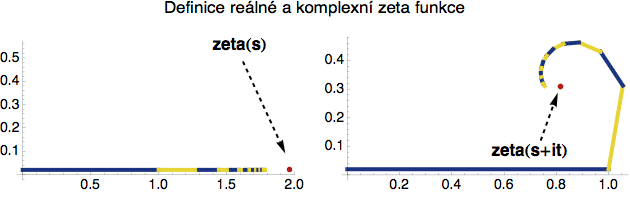
Na obrázku jsem vám samozřejmě ukázal jen prvních pár členů (tedy konečný počet). Abyste dostali hodnotu funkce zeta, musíte si je v tom nekonečném součtu představit všechny. Proto je výsledná hodnota zeta funkce, označená červeným bodem, z pohledu těch barevných „hadů“ trochu „vepředu“. Pro vyšší hodnoty s se úsečky ale zmenšují poměrně rychle, takže pro solidní aproximaci funkce zeta vám obvykle stačí sečíst doslova jen prvních pár členů, což si můžete ověřit pomocí online zeta kalkulačky) (v závorce změňte nastavené hodnoty na své vlastní a stiskněte Enter/Return).

+++++++++

Celá tahle umocňovací piškuntálie ale funguje pouze pro komplexní čísla z, pro která je reálná část s>1 (opět z důvodu konvergence - tedy konečnosti součtu té definiční řady). A to znamená, že zatím jsme si funkci zeta definovali jen v poměrně malé části komplexní roviny - viz zelená oblast v následující orientační mapce (na ní je reálný definiční obor, původně uvažovaný Eulerem, vyznačen fialově).

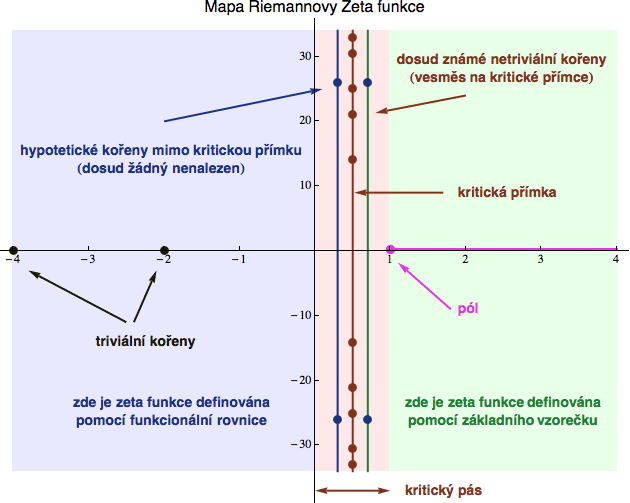(zatím se soustřeďte jen na barvu pozadí)

Minule jsme si řekli, že komplexní funkce mají tu magickou vlastnost, že se dají jednoznačně rozšířit i z poměrně malé definiční oblasti. Ony v jistém smyslu vědí, „kam chtějí jít“. Ta podmínka, aby měly komplexní derivaci, je natolik silná a svazující, že existuje pouze jeden (!) způsob jak danou funkci rozšířit, aniž by se komplexní derivace porušila. Takže z pohledu matematika je rozšíření funkce zeta do zbytku komplexní roviny garantováno komplexní analýzou. Funkci je úplně jedno, že její definiční formulka pro s<1 nefunguje. Ona se v té zelené oblasti toho o sobě dozví dostatek na to, aby své rozšíření zvládla sama (pomocí mocninných řad). Na YouTube najdete velmi hezké video, které analytické rozšíření zeta funkce popisuje bez zbytečných technických detailů (kruciální je pasáž kolem 12. minuty, kde vidíte, že pokud byste rozšíření zdeformovali, tak ztratíte hladkost komplexní funkce - místo komplexní derivace zde autor používá názornější funkční „siločáry" - ne nepodobné těm z předminulého Matykání).

+++++++++

Z pohledu normálního smrtelníka je ale myšlenka analytického „samorozšíření“ trochu divoká a abstraktní. Proto vám ukážu dvě vychytávky, které vám umožní představit si, co funkce zeta dělá ve zbytku komplexní roviny.

V první řadě se ukázalo, že zeta funkce splňuje tzv. funkcionální rovnici (4), která svazuje její hodnotu v bodě z s hodnotou v bodě 1-z. Pokud s hodnotou z projíždíte záporná reálná čísla od nuly směrem doleva, výraz 1-z projede přesně podél Eulerova původního definičního oboru (na mapce fialově). A v něm už funkci zeta známe, takže tento trik nám umožní spočítat hodnotu ve všech záporných číslech (všechno ostatní napravo v rovnici jsou pak známá čísla nebo funkce - gama funkce je rozšíření faktoriálu a definoval jsem ji v tomto Matykání). Pro zbytek modré oblasti vlevo se to udělá podobně - stačí si uvědomit, že komplexní čísla z a 1-z jsou symetrická podle bodu z=1/2 (spočítejte si jejich aritmetický průměr!), takže kdykoliv číslo z leží v modré části, číslo 1-z bude ležet v části zelené a tam už máme funkci zeta spočítanou. Pronásobením všech členů napravo ve formulce (4) pak dostaneme hodnoty funkce zeta v modré části komplexní roviny: Re(z)<0.

Jediný kousek komplexní roviny, kde nám tento fígl neprojde, je červená oblast (kde je reálná část komplexního čísla mezi 0 a 1). Tato oblast totiž leží ve „srážkovém stínu“ funkcionální rovnice (4). Komplexní čísla z v její levé polovině (0<s<1/2) se odkazují na čísla 1-z, která budou ležet v polovině pravé (1/2<s<1). A ani pro jedny zatím neumíme zeta funkci popsat.

A jak už to tak bývá, to nejzajímavější na funkci zeta se odehrává právě v této části komplexní roviny, které se proto říká „kritický pás“ (angl. critical strip). Naštěstí není všechno ztraceno, i v této „zemi nikoho“ se dá to tajemné „analytické samorozšíření“ popsat poměrně explicitně pomocí Dirichletovy eta funkce - viz vzoreček (5).

Ta je definována prakticky stejnou řadou jako funkce zeta, jen se v ní pravidelně střídají znaménka. To má za následek, že se dá explicitně spočítat i pro hodnoty z, jejichž reálná část je menší než jedna (ale větší než nula). Intuitivně to není nic překvapivého. Pokud v té řadě tu něco přičteme, tu zase odečteme, můžeme si dovolit podstatně nižší rychlost zmenšování jejích členů, než když stále jen přičítáme.

Nejlépe je to vidět na harmonické řadě se střídavými znaménky:

1 - 1/2 + 1/3 - 1/4 + 1/5 - 1/6 + ...

Tato řada definuje funkci eta v bodě 1 a na rozdíl od standardní harmonické řady konverguje k hodnotě ln(2), což se dá ukázat pomocí mocninných řad logaritmu.

Eta funkce se tedy dá definovat přímo ze vzorečku pro Re(z)>0, což je sjednocení zelené a červené oblasti. Navíc mezi eta funkcí a funkcí zeta existuje poměrně jednoduchý vztah (6), který můžete použít pro definici zeta funkce v kritickém pásu a pro analýzu jejího chování v něm.

Není to ani nijak zvlášť těžké. Když si dvě definiční řady pro eta i zeta funkci odečtete (rovnice (2) - rovnice(5)), liché členy vpravo se vymlátí a z těch sudých si vytknete dvojku (na příslušnou mocninu), čímž dostanete další kopii zeta funkce (jako když ze sudých čísel vytknete dvojku a dostanete kopii celých čísel). No a pak už to za pomoci středoškolské lopaty lehce domlátíte do tvaru (6). Oproti tomu, odvození funkcionální rovnice (4) je poměrně obtížné a rozhodně nedoporučuji se do toho pouštět holýma rukama.

Tímto je zeta funkce definována v celé komplexní rovině jakž takž konstruktivně.

Aleluja!

+++++++++

Pokud vám takový přístup připadá jako magie, zkuste se na to podívat přes částečné součty S(N). Zafixujeme si pevně komplexní číslo z=s+it a definujeme:

S(N) = součet prvních N členů v definiční formulce (2)

Pak v té zelené oblasti částečné součty (modré body) konvergují k červeně vyznačené hodnotě zeta funkce. Přitom konvergence, jak vidíte, probíhá po dostředivé spirále (vlevo máte průběh reálné části, vpravo si body představte, jak se oscilačně blíží hodnotě zeta).

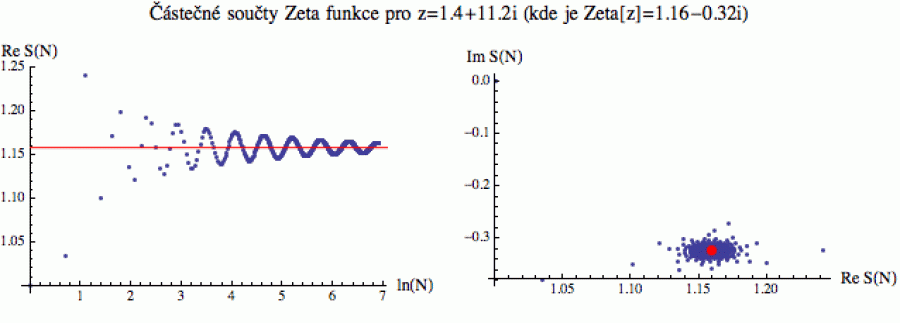
Mimo zelenou oblast řada diverguje (to znamená, že částečné součty se k ničemu neblíží), ale když se na ně podíváte podrobněji, vidíte, že se při divergenci pohybují po odstředivé spirále, která je také „ukotvena“ v hodnotě zeta funkce (spirála je zhruba exponenciála tvaru z0+exp(wt), kde z0 je hodnota zeta funkce a w vhodně zvolené komplexní číslo).

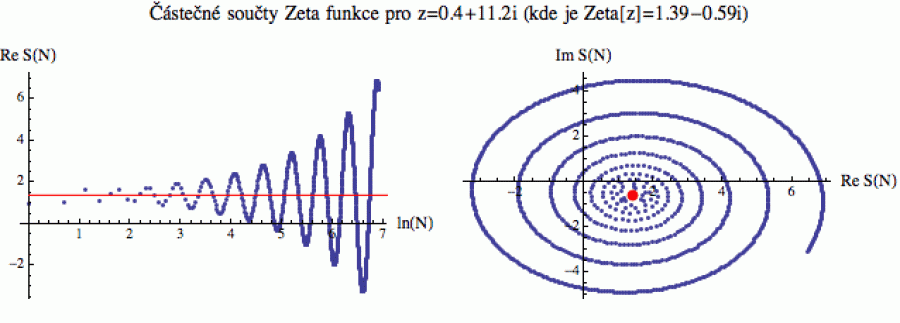
V obou případech si tedy zeta funkci můžeme v první aproximaci představit jako „osu“ spirály. Konstruktivně (součtem) se ale dá spočítat pouze tam, kde je spirála dostředivá.

Ve skutečnosti jsou částečné součty pochopitelně o něco složitější.

+++++++++

Kořeny funkce zeta

Riemannova hypotéza se týká kořenů komplexní funkce zeta, tedy komplexních čísel splňujících rovnici Zeta(z) = 0 (když je do této funkce na vstupu dosadíte, tak vám na výstupu vypadne 0).

Nejdříve si uvědomíme, že v zelené pravé části žádné kořeny nejsou, protože zeta funkce se tam dá vyjádřit pomocí výše zmíněných Eulerových součinů. A protože každý ze součinitelů je nenulový, bude nenulový i jejich součin.

Ve zbytku komplexní roviny ovšem zeta funkce nějaké ty kořeny má. A hned dvojího druhu: triviální v modré části a netriviální v červené.

Nejprve ty triviální.

Podívejte se dobře na funkcionální rovnici (4) a vyčíslete si ji v libovolném záporném sudém čísle, tj. dosaďte si do ní z=-2n, kde n je přirozené číslo. Na pravé straně se uvnitř sinu dvojky vykrátí a dostanete tam sinus v celočíselném násobku π (3.14). Každý, kdo si ze střední školy pamatuje goniometrické funkce v radiánech, ví, že sin(nπ)=0. A jakmile máte v součinu na pravé straně rovnice (4) jednu nulu, je vymalováno. Celá pravá strana je pak nula a zeta v tomto bodě (z=-2n) bude také nula. A rázem máme nekonečně mnoho kořenů - jeden pro každé záporné sudé číslo (z = -2, -4, -6, -8, -10, -12...).

Za tyhle kořeny (na mapě zeta funkce jsou vyznačeny černě) vám ovšem nikdo nedá ani cent, protože středoškolskou matematiku umí každý středoškolák (nebo skoro každý). Proto se jim také říká triviální.

Možná vám teď vrtá hlavou, proč nejsou kořeny i v kladných sudých číslech z=2, 4, 6, ..., tam bude přece sinus celočíselného násobku pí také nula. To je sice pravda, ale pro tyto hodnoty ve vzorečku zaúřaduje funkce gama. Výraz Gama(1-z) má v těchto bodech póly, které ty „další“ sinusové kořeny pěkně sežerou. „Sežrání“ funguje zhruba takto: Představte si, že studujeme kořeny součinu dvou funkcí (x)*(1/x). První funkce f(x)=x má samozřejmě kořen v nule, takže už se vám chce zvolat, že i ten součin bude mít v nule kořen. Ale ouha. Ten náš vyhlídnutý kořen v nule „sežere“ druhá funkce g(x) = 1/x, která má v nule pól. Součin obou funkcí je totiž jednička (f(x)*g(x)=1) a ta žádný kořen nemá.

Takže sečteno a podtrženo: v modré části má zeta funkce nekonečně mnoho (triviálních) kořenů v záporných sudých číslech. Žádné další kořeny už v modré části (Re(z)<0) nejsou.

+++++++++

A tím se dostáváme k vyvrcholení celého dramatu.

Všechny ostatní (netriviální) kořeny zeta funkce se musí nalézat v kritickém pásu a již více než 100 let je známo, že i těch musí být nekonečně mnoho. Kde ovšem všechny přesně leží, se zatím neví.

Riemann se ve svém článku pustil do jejich studia a všiml si, že prvních pár netriviálních kořenů se nalézá na přímce x=1/2, která ten kritický pás půlí (tato tzv. „kritická přímka“ je na mapě zeta funkce vyznačena červeně). Vyslovil proto domněnku, že všechny ostatní (netriviální) kořeny zeta funkce leží na kritické přímce, ale přiznal, že to neumí dokázat.

A ani po 150 letech se to nikomu nepodařilo, přestože se toto tvrzení, známé jako Riemannova hypotéza, stalo jedním z nejslavnějších matematických problémů a zeta funkce je pod neustálou palbou argumentů ze všech možných odvětví matematiky i fyziky.

Úplně bezvýsledná ale tato ofenziva nebyla. Dnes například víme, že prvních cca 10 bilionů netriviálních kořenů, které se zatím podařilo spočítat, na přímce skutečně leží (kdo chce pár stovek vidět na vlastní oči, mrkněte sem). Také už víme, že více než 40 % kořenů v kritickém pásu musí ležet na kritické přímce (to je ovšem podstatně slabší tvrzení než Riemannova hypotéza, která tvrdí, že na kritické přímce musí ležet všechny - tedy 100 %) a dále víme, že existují určité oblasti kritického pásu (tzv. zero-free regions), kde žádné kořeny jistojistě neleží. Zhruba řečeno jsou to oblasti, které leží u hranic kritického pásu. Pokud tedy existují nějaké kořeny mimo kritickou přímku (ty modré), neměly by ležet příliš daleko od ní.

Na mapce zeta funkce výše jsem ty již objevené netriviální kořeny vyznačil červeně a jsou přesně tam, kde mají být. Případné hypotetické kořeny mimo kritickou přímku (které by vyvrátily Riemannovu hypotézu) jsem pro ilustraci přidal k obrázku také a vyznačil je modře. Vzhledem k tomu, že žádné zatím neznáme, posadil jsem je do náhodně zvolené pozice a jejich přítomností chci hlavně říci to, že takové „bludné“ kořeny by se musely vyskytovat v pravidelných čtveřicích, jak je patrné z obrázku. Musely by být umístěny zrcadlově podle osy x a podle kritické přímky, protože zeta funkce v sobě nese určité symetrie - jedna z nich vyplývá z funkcionální rovnice a druhá ze vztahu pro komplexně sdružený argument:

Zeta(z*) = Zeta(z)*

Z laického pohledu by se mohlo zdát, že nejsnadnější cesta k milionu dolarů je prostě navštívit babku kořenářku a nějaký ten netriviální (modrý) kořen mimo kritickou přímku najít. Tím by byla Riemannova hypotéza spolehlivě vyvrácena. Ale dřív než začnete do výše zmíněné zeta kalkulačky bušit náhodná komplexní čísla z kritického pásu v naději, že objevíte zlato, vězte, že většina matematiků se shoduje, že Riemannova hypotéza pravděpodobně platí, takže lepší strategie asi bude pokusit se ji dokázat než vyvrátit.

Abychom si mohli vizuálně představit, co se v tom kritickém pásu vlastně děje, vzal jsem si tři přímky naznačené na výše uvedené mapě a všechny je pomocí zeta funkce zobrazil do výstupní komplexní roviny (tak jako jsem to pro jinou funkci udělal v první sekci tohoto Matykání - poslední dva grafíky). Tím pádem se můžete podívat, co funkce zeta provádí nejen s kritickou přímkou (červeně), ale i s přímkami těsně před ní a těsně za ní. Kořen zeta funkce bude ležet v takové hodnotě s+ti, kde ten obraz přímky projede počátkem.

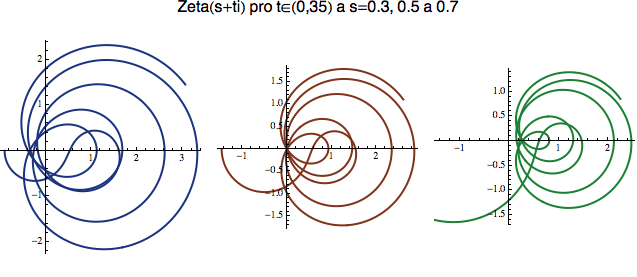
Všimněte si, že obrazy těchto tří vertikálních přímek se skládají z jakýchsi nepravidelných kudrlinek. Představte si, že jsme do počátku 0+0i zatloukli hřebík. Pro s=0.3 se všechny kudrlinky otáčí až za hřebíkem, pro s=0.7 už před hřebíkem a pro s=0.5 (kritická přímka) tím hřebíkem - jako na potvoru - projedou všechny. Jako by se rozhodly spáchat masovou sebevraždu. Pokud při jízdě podél červené křivky sledujete na tachometru hodnotu t, tak kdykoliv projedete počátkem, máte jeden kořen.

Aby bylo dynamicky vidět, jak křivky vznikají, rozvinul jsem je do tří videí.

To, co vám ukazuju, je samozřejmě jen kousek obrazu každé přímky (pro t od 0 do 90). Stále je teoreticky možné, že pro nějakou opravdu velkou hodnotu t se jedna z nečervených kudrlinek neudrží a narazí do hřebíku dříve (s<0.5) a nebo později (s>0.5), než by bylo záhodno, a to by Riemannovu hypotézu vyvrátilo. Pravděpodobnější však je, že nějaký zatím neznámý zákon umožnuje průchod počátkem pouze kudrlinkám z kritické přímky. A aby to synchronizované harakiri bylo lépe vidět, podíváme se ještě na jednu animaci, která nám ukáže, jak se modrý obrázek změní v červený a nakonec v zelený, když spojitě měníme hodnotu s. Jinými slovy, já budu tu modrou přímku v komplexní rovině pomalu posunovat doprava a animace vám ukáže, jak se postupně mění její zobrazení Riemannovou zeta funkcí.

+++++++++

Další pomůckou pro pochopení zeta funkce na kritické přímce (kde leží všechny zatím objevené kořeny) je graf absolutní hodnoty. S téčkem pojedu po kritické přímce nahoru (a jeho hodnotu vynáším níže na horizontální ose) a na vertikální ose vyznačím hodnotu zeta funkce v odpovídajícím bodě. A protože nás zajímají jen kořeny (které jsou charakterizované tím, že absolutní hodnota funkce je v nich nula), nemusíme se starat o celé komplexní číslo z na výstupu, ale jen o jeho absolutní hodnotu |z|. To je reálné číslo a bude se nám na ose y lépe vykreslovat.

A protože kudrlinky výše jsem sledoval jen do hodnoty t=35, tady se trochu rozšoupneme a v sérii pěti obrázků uvidíme chování zeta funkce na kritické přímce až do hodnoty t=500. Kdekoliv se červená křivka „dotkne“ horizontální osy, tam leží jeden z těch již objevených zeta kořenů (tady nejlépe vidíte, jak jsou netriviální kořeny chaotické - skoro jako sama prvočísla). Vyšší bochánky pochopitelně odpovídají větším kudrlinkám z předchozího obrázku, ty nižší těm menším.

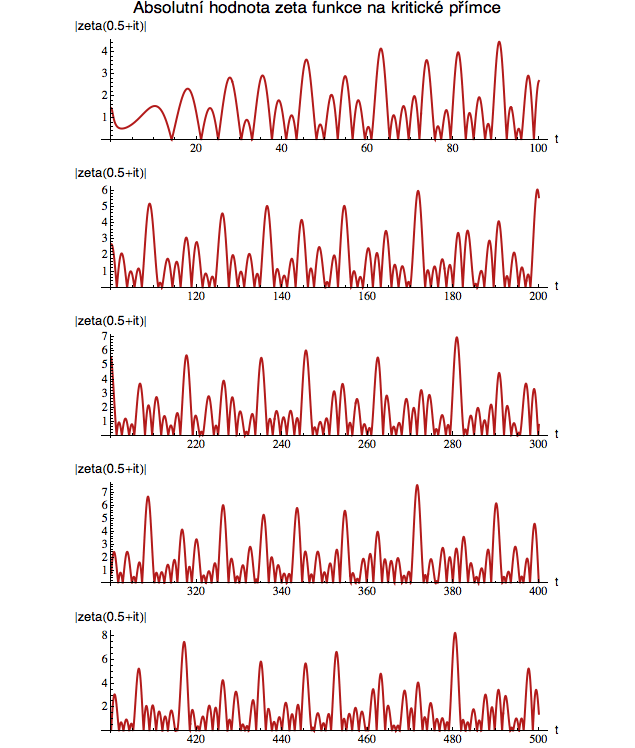
Já vím, křivka spíš vypadá jako byste pozorovali opilce vracejícího se ve dvě v noci z hospody domů a měřili odchylku jeho dráhy od středu silnice, ale je to opravdu zeta funkce. Žádná náhodně vybraná čísla jsem z její definice nevyhodil (přestože to tak vypadá).

Pokud ještě někdo pochybuje o smysluplnosti rozšíření reálných funkcí do komplexní roviny, výše uvedený obrázek by měl být dostatečným argumentem pro takovou operaci. Když si vzpomenete na fialový graf ze začátku, musíte uznat, že v reálném oboru je zeta funkce jen šedá nezáživná myška. Zato v komplexní rovině - a speciálně v kritickém pásu - rozkvete do krásy a poodhalí závoj skrývající v imaginárním oparu obrysy zrádného pohoří prvočísel. A na to konto se chová trochu jako vrtošivá operní diva. Hopsá si podél kritické přímky bez jakéhokoliv rozpoznatelného předpisu či zákonitosti a láká do svých tenat stovky nadšenců po celém světě. A nejen pro tu finanční odměnu. Ona má určité nedefinovatelné kouzlo sama o sobě. Možná i proto se každý rok objeví hned několik pokusů o důkaz Riemannovy hypotézy, zatím ale žádný z nich nebyl akceptován matematickou obcí.

Poznámka po uzávěrce: V září 2018 přednesl známý matematik a nositel Fieldsovy medaile, Michael Atiyah, svůj důkaz Riemannovy hypotézy vycházející z prací Johna von Neumanna a Friedricha Hirzebrucha - tento přístup momentálně zkoumají odborníci.

Pokud nejste zrovna příznivci teorie komplexních funkcí, můžete se pokusit shrábnout ten miliinek tím, že dokážete některou z ekvivalentních formulací, tedy tvrzení, z jejichž důkazu už by Riemannova hypotéza vyplynula (a naopak).

Tak hodně zdaru!

+++++++++

A proč je zeta funkce vlastně tak důležitá? Především, jak už jsem naznačil na začátku, prostřednictvím Eulerových součinů má v sobě zakódovány různé vlastnosti prvočísel (v jistém smyslu je dokonce klíčem pro jejich pochopení). Mnohé problémy týkající se prvočísel se dají z jejích vlastností přímo odvodit. Pomocí kořenů zeta funkce se snažíme pochopit chování tzv. prvočíselné funkce π(x) (angl. prime counting function), která počítá, kolik prvočísel se nalézá pod danou hodnotou x. Pro tuto funkci známe několik velmi dobrých aproximací (například x/ln(x)) a kořeny zeta funkce k nim v podstatě přidávají korekce, aby tyto přibližné funkce vyjadřovaly skutečné chování prvočísel (viz tato popularizační přednáška v angličtině). Pokud by se podařilo dokázat Riemannovu hypotézu, tak bychom získali daleko přesnější odhad pro chybu takových aproximací. Z pohledu laické veřejnosti je odhad takové chyby poměrně esoterickou záležitostí. Dá se ale ukázat, že Riemannova hypotéza je schopna nám o prvočíslech říci i věci, které lze pochopit bez znalosti vyšší matematiky. Například tohle: vyberte si náhodně nějaké přirozené číslo (jak chcete vysoké, klidně nějaký ten trilionek plus drobné). Toto číslo se dá samozřejmě rozložit na prvočíselné faktory a jejich počet je buď sudý, a nebo lichý (třeba pro 6=2*3 je počet faktorů sudý, pro 30=2*3*5 je lichý). Riemannova hypotéza je ekvivalentní tvrzení, že lichý i sudý počet faktorů tohoto náhodně zvoleného čísla jsou stejně pravděpodobné (bez platnosti Riemannovy hypotézy se to kupodivu dokázat nedá).

Další důvod zájmu o Riemannovu hypotézu je propojení světa diskrétních objektů (prvočísel) se zdánlivě nesouvisejícím světem spojitých funkcí (zeta funkce v komplexní rovině). Tato pozoruhodná vlastnost neunikla fyzikům, kteří se snaží pochopit přechod z mikrosvěta částic a balíčků energie do zdánlivě spojitého makrosvěta. I proto najdete Zeta znalce také v kvantové mechanice a nebo v teorii strun. A jako historickou perličku ještě dodám, že velkým příznivcem zeta funkce byl také jeden ze zakladatelů moderní informatiky, Alan Turing.

Sekce Jauvajs: 1+2+3+4+5+6+7+... = -1/12

(jen pro mimořádně otrlé povahy)

V posledních letech se na několika serverech diskutujících populární fyziku objevila pozoruhodná rovnice uvedená v titulku této sekce (viz například zde), která nám víceméně říká, že pokud sečteme všechna přirozená čísla, dostaneme -1/12.

Nesmíme to ale samozřejmě brát doslova. Ta -1/12 je s řadou sice nějakým způsobem svázaná, ale ne v tom smyslu, že by to byl přímo její zákonným součtem.

Otázka přiřazení nějakého smysluplného čísla řadám, které nekonvergují (tedy nemají konečný součet v klasickém smyslu), je poměrně důležitá, protože takové řady se občas vyskytnou při řešení různých fyzikálních úloh. A fyzikové se z pochopitelných důvodů nekonečnu vyhýbají jako čert kříži.

Takové úsilí má ale význam i z vnitřního pohledu matematiky. Podívejme se třeba na následující dvě řady:

1 + 2 + 3 + 4 + 5 + 6 + ...

1 + 4 + 9 + 16 + 25 + 36 + ...

Obě mají nekonečný součet, takže bychom je mohli charakterizovat symbolem pro nekonečno, ale přesto asi cítíte, že úplně stejné ty řady nejsou - druhá se k tomu nekonečnu prokousává podstatně rychleji.

Jak řadám s nekonečným součtem přiřadit nějaké konečné číslo, je poměrně komplikovaná otázka. Můžete zkusit jednotlivými členy této řady proložit nějaký polynom a pak zkoumat jeho vlastnosti (třeba kořeny nebo průsečík s osou y). A nebo se můžete pokusit zobecnit vlastní pojem součtu - na to je celá řada metodologií, většinou používajících různé triky na zprůměrování částečných součtů (např. abelovská či cesarovská sumace - podrobnosti zde).

My se ale na ten „divný výsledek“ z titulku podíváme pouze intuitivně - abychom nezabředli do bažiny nerovností a sumačních symbolů.

Označme si hledaný součet písmenkem S:

S = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + ...

Nejprve z něho uděláme součet řady se střídajícími se znaménky (ty se lépe manipulují) a to tak, že součet vynásobíme 4 a pak jeho členy postupně odečteme od sudých členů původní řady (liché necháme beze změny):

4S = 4 + 8 + 12 + 16 + 20 + ...

tak a teď odečteme 4 od 2, 8 od 4, 12 od 6 a tak dále až dostaneme:

S-4S = -3S = 1 - 2 + 3 - 4 + 5 - 6 + ...

Z gymnázia si vzpomeneme na vzoreček pro součet geometrické řady s koeficientem x:

1 + x + x^2 + x^3 + x^4 + x^5 + ... = 1/(1-x)

a teď celou tu rovnici, pěkně člen po členu zderivujeme:

0 + 1 + 2x + 3x^2 + 4x^3 + 5x^4 + ... = 1/(1-x)^2

takto vzniklý výraz vyčíslíme v bodě x = -1, čímž dostaneme:

1 - 2 + 3 - 4 + 5 - ... = 1/4

Jenže celá ta sranda na levé straně je náš „střídavý“ součet, který - jak jsme výše odvodili - se rovná -3S. Takže můžeme napsat:

-3S = 1/4

no a odtud vyplývá, že S = -1/12 (a je hotovo).

Úplně košer to samozřejmě nebylo. Jednak cílené odečítání (kdy jsem odečítal pouze od sudých členů) je u nekonečných řad diskutabilní a jednak formulka pro geometrickou řadu platí pouze pro -1 < x < 1, takže pro -1 už přímo použít nelze. Nicméně vidíte, že se k tomu „divnému“ výsledku lze propracovat poměrně rychle středoškolskými metodami (tedy pokud vás ve čtvrťáku naučili derivovat).

Celá tahle habaďura se dá udělat o něco přesněji a rigorózněji, v takovém případě se jí říká regularizace divergentních řad. Součet řady bude samozřejmě stále nekonečno, ale alespoň se k té jedné dvanáctině dojde legálnějšími prostředky.

Vychytralý čtenář se ale na původní řadu

S = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + ...

může podívat optikou Riemannovy zeta funkce a zauvažovat takto: pokud do definiční rovnice (1) formálně dosadíme s=-1, dostaneme přesně naši řadu S. Tu samozřejmě sečíst neumíme, ale když jsou komplexní funkce tak chytré, že se dokáží samy analyticky rozšířit i mimo rámec definiční formulky, podívejme se, jak se „přirozené rozšíření“ zeta funkce vyvrbí v bodě -1.

Takže do online Zeta kalkulačky naťukáme -1 a simsala bim:

Zeta(-1) = -1/12

To jsou věci, co?

Článek je redakčně upravenou verzí blogového příspěvku na serveru iDNES.cz. Publikováno s laskavým svolením autora.

Další díly a původní texty jsou dostupné na blogu Jana Řeháčka.

Autor: Jan Řeháček