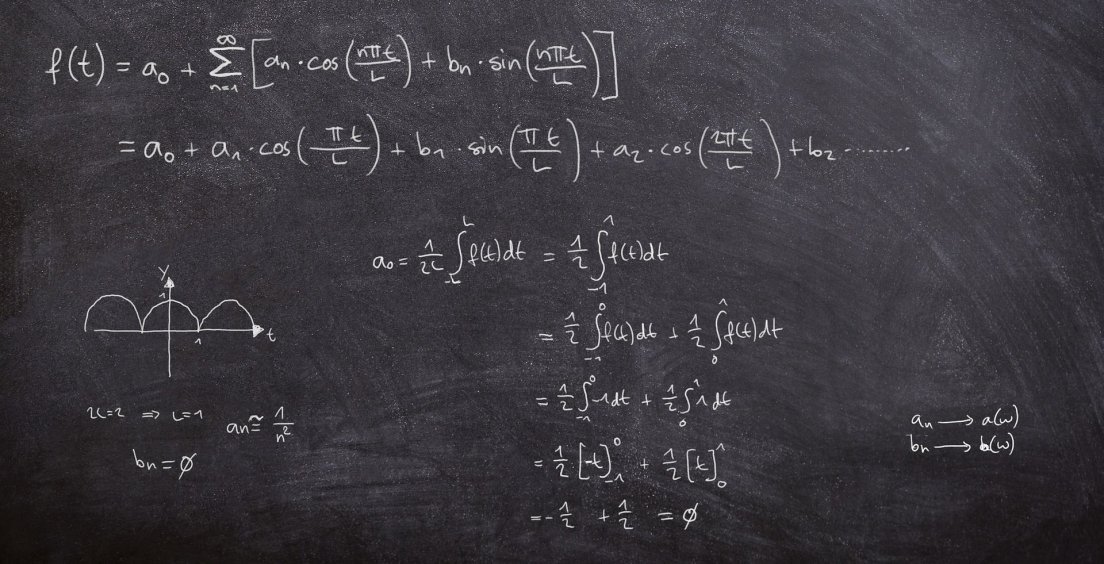Při derivování vícerozměrných funkcí musíme dávat pozor zejména na to, kolik mají vstupů a výstupů, a podle toho pak nasadit vhodnou diferenciální frézu. Dnes se v té houštině více proměnných pokusíme najít náznak nějakého řádu.
Literární předkrm: Mouchy nesnesitelně bzučely. Jako by neměly nic jiného na práci než čeřit nehybný vzduch svým vysokofrekvenčním vlněním. Bič dopoledního slunce jim ochotně sekundoval a vpaloval do kamenných zad skalní mesy krvavé podlitiny. Ochmýřené stíny nadýchaných obláčků se bojácně proplétaly arizonskou polopouští. Ve stínu skalního převisu seděla skupinka neoholených mužů. Krvavý Džejk se nuceně opíral o pichlavý kaktus saguaro a zkoumavým pohledem pozoroval výdejní otvor nabité winčestrovky, kterou mu jeden z mužů přidržoval pod nosem.
Starší kovboj v odřené vestě z jelení kůže se pomalu zvedl a přistoupil k Džejkovi: „Potřebovali bychom od vás určitou službičku.“ Džejk přičetl mdlé použití přítomného kondicionálu dotírajícímu slunci, a přestože byl všeobecně považován za největšího fajnšmekra české gramatiky na západ od Ohře, nehnul ani brvou svého větry osmahlého obličeje. „Vo co gou?“ procedil protáhle skrz zuby v rytmu dokonale sladěném se žvýkáním hrudky tabáku značky Henry Clay.
„Náš dobytek se nedostane k napajedlu, protože jediná přístupová cesta skrz Supí soutěsku vede přes vládní pozemky,“ začal opatrně starší kovboj. „A jistý James ve státním úřadu nám dělá byrokratické naschvály.“
„Jakou má funkci?“ pokračoval Džejk v akustickém přežvykování.
„Je to zástupce guvernéra pro pozemkové výměry,“ vysvětloval kovboj. „A od vás bychom potřebovali, abyste tuhle funkci nahradil nějakou jednodušší – alespoň lokálně –, řekněme, zástupce guvernéra pro přátelské vycházení s místními rančery. Nebo tak něco.“
„Kolik má ta funkce proměnných?“ vtěsnal do žvýkací periody Džejk.
„Asi tak tři, možná čtyři,“ uvažoval nahlas kovboj.
Džejk semknul rty k jedné straně, lehce zkrabatil čelo a obočí stáhl do polohy „usilovné koumání“. Jeho strážce instinktivně sklopil namířenou hlaveň, aby nenarušil neslyšné otáčení ozubených koleček v Džejkově hlavě. Starý kovboj se posadil na vyschlý kmen vyvráceného jasanu a k polozarostlé ústní dutině přiložil lesknoucí se placatici podomácku vypálené whiskey. Kdesi nad jejich improvizovaným táborem se ve skalní průrvě mihl kojot.
Po chvíli, která musela přítomným připomínat alespoň čtvrtinu věčnosti, se Džejk prohrábl svým dvoutýdenním strništěm a hrudku tabáku vyplivl do rozpáleného písku. „Dobře, já vám tu funkci lokálně nahradím,“ pokýval hlavou a na jednoho z mladších pohůnků štěkl: „Hej, kámo, dojedeš do Samuelova železářství na západním okraji města a přivezeš mi skládací gradient s ocelovým pažením a půl pinty jemného oleje na diferencování.“
Lokální lineární aproximace
Tak jako je škola základ života, je funkce základ matematiky. V průběhu Matykání už jsme jich viděli celou řadu, takže jen zopakuji, že si je můžeme představit jako černou skříňku s trpaslíkem, do jejíhož vstupního otvoru vhodíme nezávisle proměnnou x a z otvoru výstupního nám po chvíli vypadne závisle proměnná y.

Do toho otvoru samozřejmě obvykle vhazujeme čísla (pro klasické středoškolské funkce), ale v principu do něj můžeme vhodit cokoliv: vektory, matice, jiné funkce. Jednou jsem dokonce přistihl studentku Vopičkovou, jak se do vstupního otvoru snaží vhodit živou užovku.
Dnes se zaměříme na případ, kdy máme na vstupu či výstupu (nebo obou) více zdířek (jak je naznačeno na obrázku špičičkami). Vstupní či výstupní proměnnou (nebo obě) si tedy můžeme představovat jako vektor.
Jedna z prvních věcí, která nás u funkcí zajímá je spojitost. Tedy když do otvoru místo x° vhodíme malinko pozměněnou hodnotu x, do jaké míry se změní výstupní hodnota y?
Přesněji: zajímá nás, jaký je vztah mezi změnou nezávisle proměnné Δx = x-x° a změnou závisle proměnné Δy = y-y°. Tato změna se dá pro konkrétní hodnoty pochopitelně vyčíslit z definičího vztahu y = f(x), takže pro každý přírůstek Δx si lehce spočítáme příslušný přírůstek Δy.
Zobrazení Δx --> Δy převádí 0 --> 0 (což je jedna z vlastností lineárních zobrazení), takže matematiky napadlo, zda by se lokálně (v okolí bodu x) nedalo to přírůstkové zobrazení aproximovat lineární funkcí, která by Δy spočítala z přírůstku Δx přímo bez nutnosti konzultovat původní funkci f. Lineární funkce patří k těm nejjednodušším (dobře se analyzují), takže taková aproximace by nám o lokálním chování funkce f v okolí bodu x° poskytla cenné informace.
Schematicky je to na dalším obrázku zobrazeno pro funkci f: R2 --> R2 a pro pevně zvolený bod x°. To lineární zobrazení zprostředkující převod mezi přírůstky označím L (a musíme mít na paměti, že toto zobrazení závisí na x° – občas ho tam do argumentu vlípnu). A protože lineární zobrazení jsou často realizována pomocí součinu (ať obyčejného či skalárního), budu výstupní hodnotu označovat pravou stranou následující rovnice.
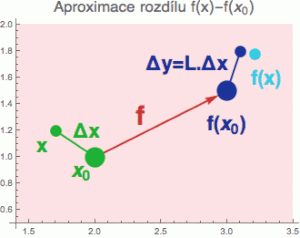
(+) Δy ~ L(Δx) = L(x°).Δx
(kde znak ~ znamená přibližnou rovnost)
Důležité je uvědomit si, že lineární zobrazení L funguje na „přírůstcích“ příslušných proměnných, nikoliv přímo na jejich hodnotách. Tohle si dobře rozmyslete.
A za zopakování stojí tohle: to Δy zde není technicky vzato přímo ten přírůstek – ten bychom získali odečtením tmavomodrého bodu f(x°) od bleděmodrého f(x). Je to pouze jeho lineární aproximace.
Význam formulky (+) spočívá v tom, že nám umožňuje obejít funkci f a provést rychlý výpočet Δy (byť jen přibližný) pro všechny lokální hodnoty Δx najednou. Tím pádem nám dává i rychlé lokální aproximace funkce f:
f(x) ~ f(x°) + L(x°)Δx
(pravá strana je ta malá tmavomodrá kulička na obrázku)
Zobrazení definované rovnicí (+) reprezentuje derivaci funkce v bodě x° (pro celkem zábavnou diskusi standardní terminologie mrkněte sem). V případě klasické středoškolské funkce jedné proměnné se pochopitelně místo L(x°) používá značení f'(x°), protože v jednorozměrném případě je lineární funkce v podstatě reálné číslo č. Derivace funkce f je pak prostě funkce f': x° --> č, kde pravou stranou rozumíme lineární funkci y = čx, která převádí Δx na Δy.
Pokud je ve hře více proměnných, musíme být s derivacemi opatrnější. Abstraktní pohled, kdy se na derivaci díváme jako na lineární převodovou funkci, se nám bude hodit.
Abychom diskusi moc nekomplikovali, dohodneme se na určitém rámci. Pokud má funkce na vstupu nebo výstupu více proměnných, budeme je považovat za vektor (tj. těch n hodnot prostě sbalíme do jednoho vektorového rance) a při zavádění derivace pak budeme rozlišovat následující 4 případy (z typografických důvodů budu n-rozměrný prostor značit R3 – jen si místo té 3 představte n – ono se s trojicemi pracuje zhruba stejně jako s n-ticemi):
1. Funkce jedné proměnné
f: R --> R
(skalár na skalár)
2. Křivky
f: R --> R3
(skalár na vektor)
3. Funkce více proměnných
f: R3 --> R
(vektor na skalár)
4. Vektorová pole
f: R3 --> R3
(vektor na vektor)
V každém z těchto případů se podíváme, jak lineární zobrazení L, které převádí x-přírůstky na y-přírůstky, funguje. A jak tedy vlastně funguje i derivace.
Případ 1 už jsme viděli několikrát (viz zde a zde, nebo komplexně zde). Přesto bych vám doporučil nakreslit si tečnu k nějaké funkci f v bodě A = (x°,f(x°)) a rozmyslet si, jak ta tečna (coby lineární funkce s počátkem v bodě A) převádí přírůstky (vztažené k bodu A) na sebe.
A teď už se podívejme na případ 2 – křivky. Křivka v n-dimenzionálním prostoru je popsána n funkcemi jedné proměnné (označené t, neboť má obvykle význam času). Rovinná kružnice je např. popsána dvojicí funkcí:
x(t) = cos(t)
y(t) = sin(t)
Prostorová spirála trojicí:
x(t) = cos(t)
y(t) = sin(t)
z(t) = t
(jak bod cestuje po kružnici, tak rovnoměrně s časem stoupá ve směru osy
z)
Někdy se tyto funkce pro jednoduchost zabalí do polohového vektoru křivky:
r(t) = (x(t), y(t), z(t))
Každý bod P této křivky pak odpovídá určité konkrétní hodnotě parametru t.
Definiční funkce obsahují pouze jednu proměnnou, takže s derivováním nejsou žádné potíže:
x'(t) = -sin(t)
y'(t) = cos(t)
z'(t) = 1
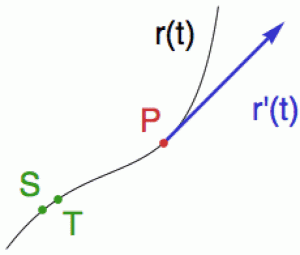
a derivace jednotlivých složek můžeme opět pro pohodlí zabalit do vektoru
r'(t) = (-sin(t), cos(t),1)
Protože derivace složek ukazují, jak rychle se každá z nich mění s parametrem t (s časem), derivace polohového vektoru je tečný vektor ke křivce v bodě odpovídající parametru t (viz obrázek vpravo).
To vyplývá z toho, že na tečný vektor můžeme z pohledu definice pohlížet jako na rozdíl infinitesimálně vzdálených bodů na křivce (příslušně přeškálovaný) a jako takový bude mířit ve směru křivky. Označíme-li si S = r(t°) a T = r(t), můžeme limitu v definici derivace zapsat přibližně takto:
r'(t) ~ (r(t) - r(t°)) / (t-t°) =
(T-S)/Δt
(a z obrázku je patrné, že pro malá Δt běží vektor T-S
podél křivky)
Z pohledu rovnice (+) je tedy derivace rovinné křivky v bodě odpovídajícímu parametru t° její tečný vektor r'(t) vyčíslený pro tuto hodnotu parametru. Tento vektor převádí přírůstky nezávisle proměnné (t) na přírůstky závisle proměnné (r):
(+) Δr ~ r'(t°) Δt
To, že zobrazení L (definované pravou stranou), které skaláru Δt přiřadí vektorový přírůstek r'(t°)Δt, je lineární v proměnné Δt, si můžete lehce ověřit sami.
Je-li tedy tečný vektor k nějaké křivce v bodě t° = 1 roven r'(1) = (1, 2, 3), pak při změně parametru na t = 1.1 (tj Δt = 0.1) by se poloha bodu běžícího po této křivce měla změnit zhruba o (1, 2, 3) * 0.1 = (0.1, 0.2, 0.3).
Můžete si to zkusit pro výše uvedenou spirálu sami. Nejprve si spočítejte, kde jsou polohové vektory pro t° = 1 a t = 1.1 a odečtením získáte přesný nárůst Δr. Pak si spočítejte tečný vektor r'(t°) a z formulky (+) získáte přibližnou hodnotu Δr.
Funkce více proměnných
V životě se lehce přihodí, že nějaká funkce závisí na dvou či více neznámých, tedy do trpaslíkovy skříňky musíme vhodit dvě či více vstupních čísel, abychom z ní vyždímali výstupní hodnotu.
Tady už klasické derivování použít nemůžeme a nadto je těžko říci, co by taková derivace měla vlastně znamenat.
U funkcí jedné proměnné je to jednoduché. Její nezávisle proměnná žije na ose x, která je uspořádaná, takže lze mluvit o tom, zda na ní funkce roste či klesá (tedy zda se zvětšujícím se x bude y růst či klesat a jak rychle).
Funkce více proměnných jsou definované na vícerozměrném eukleidovském prostoru (rovina xy, prostor xyz atd.) a zde už přirozené uspořádání neexistuje, a lze tudíž těžko říci, kdy funkce roste či klesá.
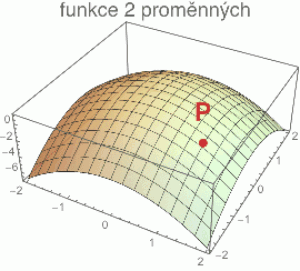
Podívejme se na příklad jednoduché funkce dvou proměnných
z = f(x, y) = 1 - x2 - y2
Do skříňky tedy vhodíme dvě čísla (x, y) a na výstupu dostaneme hodnotu z spočítanou dle funkční formulky. Graf takové funkce (na obrázku vpravo) si nejlépe představíme jako plastickou 3d mapu, kde x a y vybíráme z roviny a z pak vynášíme na svislou osu.
Pokud se postavím do bodu P, tak vůbec není jasné, zda funkce v daném bodě roste anebo klesá. Stojíme v podstatě na úbočí Řípu a o tom, zda budeme stoupat nebo klesat rozhoduje to, jakým směrem se vydáme.
Jakmile si směr zafixujeme, tak už se můžeme začít bavit o tom, zda v něm funkce roste nebo klesá a jak rychle. Podobně jako když si v horách turistickou holí vytyčíte určitý směr, tak hned vidíte, zda podél něho půjdete nahoru nebo dolů.
Pokud si pro bod P = (x°, y°, f(x°, y°)) označíme dvojici proměnných
p = (x°, y°) a směr vektorem u, tak pro
směrovou derivaci Df v bodě p se dá sestavit podobná
limita jako pro klasickou jednorozměrnou derivaci – koneckonců jakmile si
zafixujeme směr (třeba jednu z těch tečkovaných linií), tak na něm už
funkce vypadá jako obyčejná funkce jedné proměnné (linie promítnutá do
roviny supluje osu x). Směrová derivace se pak definuje takto:
Df(p) = lim ( f(p +
tu) - f(p) ) / t
(v limitě se t blíží jako obvykle k nule)
Protože funkce f má na výstupu skalár z, je výše uvedená hodnota také skalárem.
Význam směrové derivace je podobný jako význam derivace pro funkce jedné proměnné. Je-li hodnota směrové derivace, řekněme, 3, pak to znamená, že posuneme-li se ve směru u o nějakou malou vzdálenost h (a tu vzdálenost měříme průmětem do roviny xy), pak funkční hodnota vzroste zhruba o hodnotu 3h.
Počítat ale rychlost růstu vícerozměrné funkce v každém směru u je těžkopádné. Naštěstí se směrové derivace v bodě p chovají jako vektory, tj. všechny je můžeme vyčíslit ze znalosti derivací v určitých bázových směrech. Vděčíme za to linearitě, tedy tomu, že při zkoumání růstu de facto nahrazujeme křivočarou plochu funkce v okolí bodu P tečnou rovinou.
Za bázové směry si zvolíme směry souřadných os (zde x a y), aby byly obdržené formulky co nejjednodušší. Pro obě „bázové“ derivace používáme speciální symbol ∂ (namísto d) a říkáme jim parciální (speciální symbol nás varuje, že funkce kromě proměnné, podle které derivujeme, ještě závisí na dalších).
Df[(1,0)](p) = ∂f/∂x(p)
Df[(0,1)](p) = ∂f/∂y(p)
Tyto derivace si můžete spočítat buď limitou, anebo ze standardních jednorozměrných vzorečků tak, že druhou proměnnou (podle které momentálně nederivujete) budete považovat za konstantu (to není nic překvapivého – pokud pochodujeme ve směru osy x, pak se y skutečně nemění).
Podívejme se na příklad:
f(x, y) = 1 - x2 + 2xy
Pro vyčíslení derivace podle x se na písmenko y budeme dívat jako na konstantu (představujte si, že symbol „y“ je prostě jen zápis konkrétního čísla – podobně jako 2 nebo 3)
∂f/∂x = -2x + 2y
(pokud to není jasné, představte si tam na chvilku místo y číslo 3)
Pro derivaci podle y první dva členy vypadnou, protože i na výraz x2 se díváme jako na čtverec nějakého konkretního čísla, třeba 32. Druhý člen je pevné číslo (2x) krát y, takže derivací dostaneme jen pevné číslo (2x), podobně jako derivací výrazu 17y (podle y) bychom získali 17. Takže:
∂f/∂y = 2x
Budeme-li chtít tyto derivace vyčíslit v nějakém konkrétním bodě P, dosadíme do těchto výrazů obvyklým způsobem. Pro p = (2, 1) dostaneme
∂f/∂x(p) = -2
∂f/∂y(p) = 4
Vyrazíme-li tedy z bodu P ve směru osy x, budeme pomalu klesat, ve směru y budeme naopak poměrně rychle stoupat.
Podobně jako pro křivky se vyplatí tyto dílčí „bázové“ derivace zabalit do vektoru, kterému říkáme gradient funkce f
grad(f) = (∂f/∂x, ∂f/∂y)
s tím, že pro konkrétní bod p dostaneme konkrétní číselný vektor grad(f)(p).
Tohle zabalování je ale trochu jiné než pro křivky. Tam jsme balili derivaci různých souřadných funkcí podle stejné proměnné t. Tady balíme derivaci stejné funkce f podle různých proměnných x, y, ...
A jak si gradient představovat? V každém konkrétním bodě p nám ukazuje směr (gradient je vektor stejné dimenze jako prostor nezávisle proměnných), ve kterém funkce nejrychleji roste.
To je vidět z toho, že derivace v jednotkovém směru u (a každý nenulový směr se dá normalizovat) se dá spočítat z gradientu skalárním součinem
Df[u] = grad(f) . u
(tato formulka je v podstatě vyjádřením toho, že směrová derivace je
lineární kombinací „bázových“ derivací, kde složky vektoru
u hrají roli koeficientů)
a budete-li u opatrně otáčet, tak tento výraz bude maximální právě v případě, kdy směr u bude odpovídat směru vektoru grad(f), což je obvyklá úvaha o průmětu jednoho vektoru do druhého (průmět je maximální pro kolineární vektory).
Pro funkci z předchozího příkladu je tedy gradient v bodě p = (2, 1) roven
grad(f) = (-2, 4)
a to je směr, ve kterém funkce f v bodě p roste nejrychleji (všimněte si, že komponenta x je záporná: podél x budeme muset „couvat“, neb směrem dopředu funkce v tomto směru klesá).
Pokud si rádi hrajete, můžete si nabrnkat spoustu jednotkových směrů (pro různé úhly α)
u = r (cos(α),sin(α))
(kde r je nějaké malé číslo, třeba 0.1)
a spočítat si hodnotu funkce v bodech f(p + u) a uvidíte, že nejvíce funkční hodnota vzroste (oproti bodu p), když bude u skalárním násobkem gradientu.
Takže formulka (+) z úvodu, podle které můžeme převést přírůstky nezávisle proměnných na přírůstek závisle proměnné, bude
Δz ~ ((∂f/∂x,∂f/∂y).(Δx,Δy)
Lineární zobrazení (které převádí jedny přírůstky na druhé) zde tedy funguje v podstatě jako směrová derivace, kde přírůstek nezávisle proměnných de facto určuje směr Δu = (Δx,Δy).
L: Δu --> grad(f).Δu = Df[Δu]
Jak pro případ 2, tak pro případ 3 jsme tedy získali derivaci ve formě vektoru. Rozdíl je v tom, že pro křivky jsme tečný vektor vynásobili přírůstkovým skalárem (a dostali tak vektor polohového přírůstku), zatímco zde jsme vektor gradientu grad(f) vynásobili skalárně přírůstkovým vektorem (a dostali tak skalár funkčního přírůstku).
Vektorová pole
Závěrem se podíváme na případ 4, kdy budeme pracovat se skříňkami, které mají na vstupu i výstupu několik zdířek. Jako příklad si vezmu pole třírozměrné, tedy zobrazení z R3 do R3, ale obecně můžete mít na vstupu i výstupu libovolný počet proměnných (ne nutně stejný).
Vektorová pole slouží primárně k popisu silových polí v 3D prostoru. Na vstupu musíme v takovém případě zadat vektor polohy (x, y, z) a na výstupu nám vypadne nikoliv skalár, ale vektor F = (f, g, h), ukazující velikost a směr síly působící v bodě (x, y, z). Na dalším obrázku je pro ilustraci několik 2D vektorových polí: každá šipčička odpovídá vektoru (f, g), zatímco poloha její paty odpovídá vstupní dvojici (x, y).
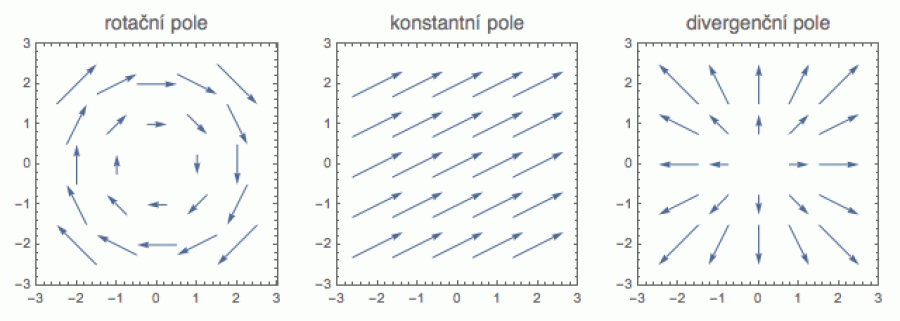
Tak jak měníme polohu, mění se i vektor síly, a všechny jeho složky jsou tudíž funkcemi souřadnic.
Ve 3D budeme tedy zkoumat lokální aproximace funkce
F: (x, y, z) --> (f, g, h)
či přesněji
F(x, y, z) = (f(x, y, z), g(x, y, z), h(x, y, z))
v nějakém konkrétním bodě a = (x°, y°, z°).
Použijeme podobný trik jako u křivek. Tři složkové funkce f, g a h jsou každá funkcí tří proměnných (viz předešlá sekce) a jejich derivace jsou tedy tři gradienty. Gradienty (což jsou vektory) úhledně poskládáme do tabulky a dostaneme tzv. Jacobiho matici, která bude hrát roli derivace (a převodového zobrazení L) pro vektorová pole.
To, že je zde derivace maticí, nás nepřekvapí, protože přírůstek jak nezávislé, tak závislé proměnné je vektor a lineární zobrazení (+), které převádí vektory na vektory, je v podstatě matice. Ta Jacobiho má v i-tém řádku gradient i-té složky (tj. derivace podle všech proměnných). Ve 3D vypadá takto:
∂f/∂x,∂f/∂y,∂f/∂z
∂g/∂x,∂g/∂y,∂g/∂z
∂h/∂x,∂h/∂y,∂h/∂z
kde všech 9 prvků této matice je vyčísleno v bodě a° = (x°, y°, z°), ve kterém derivaci (tj. Jacobiho matici) hledáme, respektive ve kterém hledáme lokální lineární aproximaci. Pochopitelně, pokud se přesuneme do jiného bodu a, tak tam nám to vyčíslení dá úplně jinou matici, což očekáváme. Lineární zobrazení, které převádí nezávislé přírůstky na závislé, se mění bod od bodu (to je koneckonců pravda i pro funkce jedné proměnné, kde se tečna při pochodu podél funkce taktéž mění).
Podívejme se na příklad. Vezmeme si nějaké konkrétní vektorové pole v R3:
F(x, y, z) = (x2 + y2 - z2,
2 * x * y + z2, 3 * x * y - z2)
(zde už jsou složky f, g, h nahrazeny konkrétními funkcemi)
Prvky Jacobiho matice J(x, y, z) budou následující:
2 x, 2 y, -2 z
2 y, 2 x, 2 z
3 y, 3 x, -2 z
Teď si vybereme nějaký bod, v jehož okolí budeme funkci F studovat, řekněme a° = (1, 1, 1). Lehce si spočítáme, že F(a°) = (1, 3, 2). Abychom pro tu funkci získali nějaký intuitivní cit, potřebujeme vědět, jak se budou chovat přírůstky, když do bodu a° trochu „drkneme“.
Nuže, vyčísleme si Jacobiho matici v bodě a°, tedy J(1, 1, 1)
2, 2, -2
2, 2, 2
3, 3, -2
Teď do toho bodu a° trochu „drkneme“ a budeme uvažovat bod
a = (1.1, 1, 1.1), což znamená, že nárůst nezávisle proměnné odpovídá vektoru
Δa = (0.1, 0, 0.1)
Závisle proměnná, funkční hodnota F, se tedy zvětší přibližně o hodnotu
ΔF ~ J(a).Δa
(toto je vektorový ekvivalent rovnice (+), kde Jacobiho matice hraje roli
lineárního zobrazení L)
A nyní tu číselnou matici J(1, 1, 1) pronásobíme skalárně přírůstkovým vektorem:
ΔF ~ J(1, 1,1 ).(0.1, 0, 0.1) = (0, 0.4, 0.1)
Nezapomeňte, že tohle není hodnota funkce v „drknutém“ bodě a. Tohle je pouze aproximace přírůstku. Z něho však můžeme hodnotu v drknutém bodě lehce odhadnout
F(a) ~ F(a°) + ΔF = (1, 3, 2) + (0, 0.4, 0.1) = (1.0, 3.4, 2.1)
Tu drknutou funkční hodnotu si pro kontrolu můžeme spočítat přesně z definice
F(a) = (1.00, 3.41, 2.09)
Vidíte, že Jacobiho matice aproximuje lokálně tu funkci docela dobře. A kdybychom to drknutí zvolili ještě menší, aproximace by byla ještě přesnější.
Jacobiho matice, zprostředkující převod mezi přírůstky, obsahuje 3x3 parciálních derivací (obecně MxN, kde M je dimenze nezávislé proměnné a N dimenze proměnné závislé).
Z takového množství informací se pochopitelně dají vykouzlit další užitečné veličiny (zde kombinace různých parciálních derivací), lokálně charakterizující vektorová pole.
Ve fyzice se často setkáte s těmito dvěma:
divergence pole F
div(F) = ∂f/∂x + ∂g/∂y + ∂h/∂z
a rotace pole F (v angličtině značená curl(F)))
rot(F) = (∂h/∂y - ∂g/∂z, ∂f/∂z - ∂h/∂x, ∂g/∂x - ∂f/∂y)
Divergence je skalár, který ukazuje jak moc z daného bodu (ve kterém jsme provedli vyčíslení derivací) vektorové pole „vytéká“ – a to ve smyslu pravé části 2D ilustrace v úvodu sekce. Rotace je vektor, jehož velikost a směr ukazuje osu maximální circulace vektorového pole, zhruba ve smyslu levé části zmíněné ilustrace.
Můžete si sami ověřit, že 3D verze pravé části ilustrace (z úvodu sekce)
F(x, y, z) = (x, y, z)
má nulovou rotaci a nenulovou divergenci, zatímco 3D verze levé části
F(x, y, z) = (y, -x, 0)
má nenulovou rotaci a nulovou divergenci.
Vzoreček pro rotaci se poměrně špatně pamatuje, takže si matematici vypomohli tzv. abstraktním operátorem nabla, což je v podstatě jenom taková notační pomůcka (košíček s abstraktními symboly derivací, chcete-li). Sám o sobě tento operátor žádný význam nemá, ba nemá ani směr (i když je to nominálně vektor), ale s jeho pomocí můžeme výše uvedené vzorečky přepsat do velmi kompaktního tvaru. Jeho definice je jednoduchá – jsou to formální parciální derivace podle všech proměnných. Ve 3D případě:
∇ = (∂/∂x, ∂/∂y, ∂/∂z)
s tím že kdykoliv danou derivaci „pronásobíme“ nějakou funkcí, tak místo součinu prostě aplikujeme naznačenou derivaci na tu funkci. S tímto formalismem se pak dají fyzikální diferenciální operátory přepsat takto:
div(F) = ∇.F = (∂/∂x, ∂/∂y, ∂/∂z) . (f, g, h) = ∂f/∂x +
∂g/∂y + ∂h/∂z
rot(F) = ∇xF = ... (to si roznásobte sami :-)
(divergence obsahuje skalární, rotace vektorový součin)
Oba tyto operátory se podstatným způsobem využívají v Maxwellově formulaci rovnic elektromagnetického pole.
Zatímco divergenci lze definovat pro libovolný počet proměnných, rotace má smysl pouze ve 3D případě, protože využívá vektorový součin a ten se do vyšších dimenzí zobecňuje obtížně.
Dokonce i gradient skalární funkce f lze zapsat pomocí nabla operátoru:
grad(f) = ∇f
kde na pravé straně stojí násobek skaláru f a vektoru ∇.
Výsledkem je pak vektor: grad(F).
Článek je redakčně upravenou verzí blogového příspěvku na serveru iDNES.cz. Publikováno s laskavým svolením autora. Další díly a původní texty jsou dostupné na blogu Jana Řeháčka.