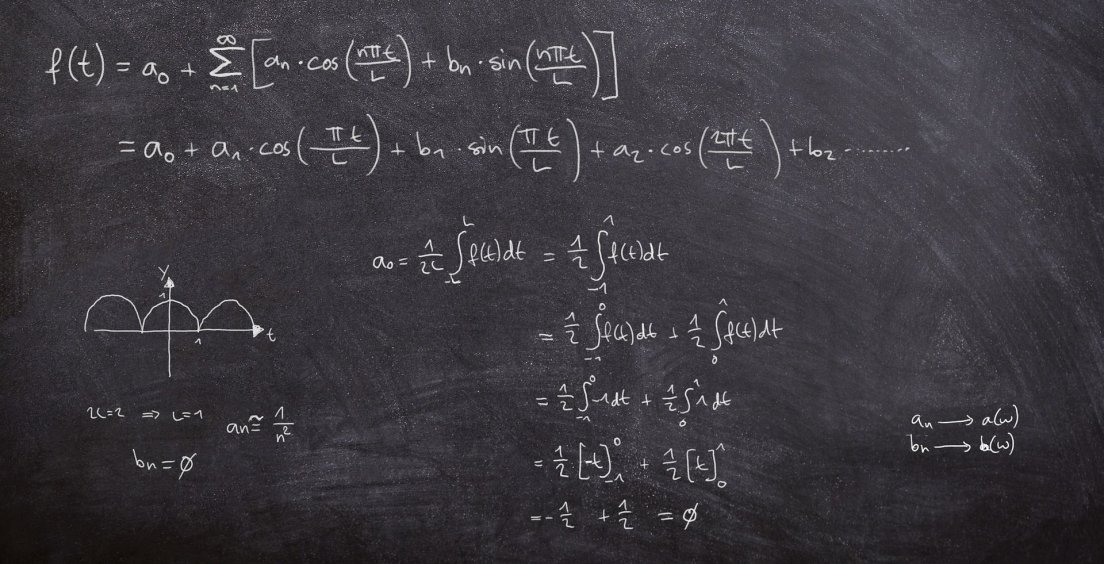Hudbou jsme začali a hudbou se také rozloučíme. Všechno, co jsem vám chtěl o matematice sdělit, už jsem vyslepičil, takže je čas nalít si skleničku, natáhnout si nohy a uvolnit se. Poslední Matykání už neobsahuje žádné integrály.
Hudba je pozoruhodná směs řádu a chaosu. Má svou strukturální kostru, jak rytmickou, tak harmonickou, ale nad ní se obvykle vznáší neklidné plaménky improvizace. Hudba v sobě musí obsahovat elementy předvídané, aby nás lapila do svého objetí, i nepředvídané, aby nás z toho objetí nepustila.
Hudební struktury, které by byly zcela pravidelné – jako když přes hudební osnovu namalujete sinusoidu – by asi moc zábavné nebyly. Mohli bychom sinusoidy sice trochu nakombinovat (ukázka je níže), ale pořád by to bylo příliš pravidelné. Ideální strukturou pro hudební matematické hrátky jsou prvočísla (respektive faktorizace celých čísel), protože ta jsou lokálně na číselné ose rozložena poměrně náhodně, ale globálně mají velmi přesné asymptotické vlastnosti (tj. stoupnete-li si do nějakého čísla Č, dá se velmi dobře předpovědět, kolik prvočísel bude pod vámi, tj. menších než Č).
Z prvočísel se dá našlehat hudba mnoha způsoby. Například můžete postupovat podél číselné osy a v každém prvočísle p rozeznít činel. Kromě polohy je dalším náhodným faktorem v charakteristice prvočísla p rozklad předchozího čísla na prvočinitele. Která čísla se v té faktorizaci p-1 vyskytují, se dá také předvídat jen velmi obtížně – takže to trochu podpoří jazzový charakter kompozice. Proto jsem přidal basu tam, kde je p-1 dělitelné 3, a klavír tam, kde je p-1 dělitelné 7. Akord klavíru je pak určen rozdílem poloh prvočísel následujících. Např. je-li prvočíslem 37 (takže následující jsou 41 a 43), pak číslu 37 bude přiřazen první tón (C), 41 čtvrtý tón (F) a 43 tón šestý (A). Ukázka tohoto postupu:
Prakticky vše, co nějak souvisí s faktorizací, v sobě obsahuje semínka náhodnosti. V tomto Matykání si budu hrát se speciálními objekty – s celočíselnými body na rotačním hyperboloidu, které v jistém smyslu kódují faktorizací komplexních čísel tvaru z + i, ale s tím vás už moc unavovat nebudu (souvisí to s jedním slavným prvočíselným problémem – č. 4 v tomto Matykání).
Nejprve ale malou technickou poznámku: rotační hyperboloid není úplně to samé co pseudosféra (která vznikne rotací speciální křivky zvané „tractrix“), takže název dnešního Matykání je trochu zavádějící. Obě plochy však mají zápornou křivost (a vládne v nich tudíž hyperbolická geometrie), takže mi tuhle nepřesnost můžete odpustit. Ono „Hudba rotačních hyperboloidů“ nemá tak hezký zvuk. A hudba je přece o zvuku, ne?
Hudba na rotačním hyperboloidu
Rotační hyperboloid není nic jiného než plocha v třírozměrném prostoru, popsaná rovnicí: x2 + y2 - z2 = 1. Je to tedy množina bodů, jejichž souřadnice (x, y, z) tuto rovnici splňují. Získáme ji tak, že běžnou hyperbolu x2 - y2 = 1 roztočíme kolem osy y.
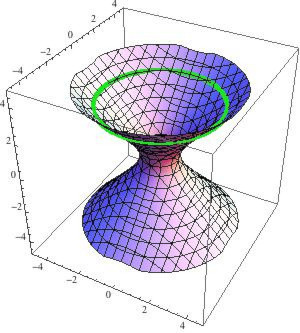
Když budeme chvíli pátrat, zjistíme, že na této ploše existuje spousta bodů s celočíselnými souřadnicemi – namátkou (8, 9, 12), (26, 15, 30) nebo (34, 47, 58). Jen si je zkuste dosadit a uvidíte. Abychom se v nich ale nějak vyznali, rozdělíme si celý hyperboloid na určité „letové hladiny“, tedy množiny bodů, které mají stejnou souřadnici z. Nalézají se tedy ve stejné výšce – jako nějaké letadlo (na obrázku vlevo je jedna konkrétní letová hladina vyznačena zeleně).
Protože třírozměrné kreslení se těžko realizuje, promítneme si pro jednoduchost všechny letové hladiny do „podlahy“ – tedy do souřadné roviny x-y. To uděláme prostě tak, že zapomeneme třetí souřadnici, takže z bodu (8, 9, 12) nám vznikne bod (8, 9) a všechny letové hladiny se změní na soustředné kružnice (viz další obrázek vpravo). Každá letová hladina je určena svou souřadnicí z – technicky je to tedy kružnice se středem v počátku a poloměrem sqrt(1 + z2).
V tomto Matykání budu uvažovat pouze letové hladiny odpovídající sudým číslům. Díky tomu budou mít všechny body (x, y) jednu souřadnici sudou a jednu lichou. Pokud ta sudá bude x, obarvím bod modře, pokud bude sudé y, vybarvím ho červeně. Z dalšího obrázku je patrné, že modré a červené body jsou symetrické – například modrému bodu (8, 9, 12) v letové hladině 12 odpovídá červený bod (9, 8, 12). Na tomto obrázku vidíme všechny celočíselné body v prvním kvadrantu (v těch dalších je to symetrické) pro letové hladiny od 2 do 60 (pouze sudé).
V první řadě si všimněte, že na tom hyperboloidu existují triviální celočíselné body, které mají buď formu (z, 1, z) pro sudé z, anebo formu (1, z, z) – to je ta modrá horizontála na obrázku (začíná bodem (2, 1, 2) a dál pokračuje jen sudými hodnotami z), resp. červená vertikála. Tyto body z našeho hudebního snažení vyhodíme a soustředíme se pouze na netriviální body se sudou hodnotou x. To jsou ty zbylé modré body (vypadají trochu jako vnitřek flašinetu a na tom bude celá akce založena).
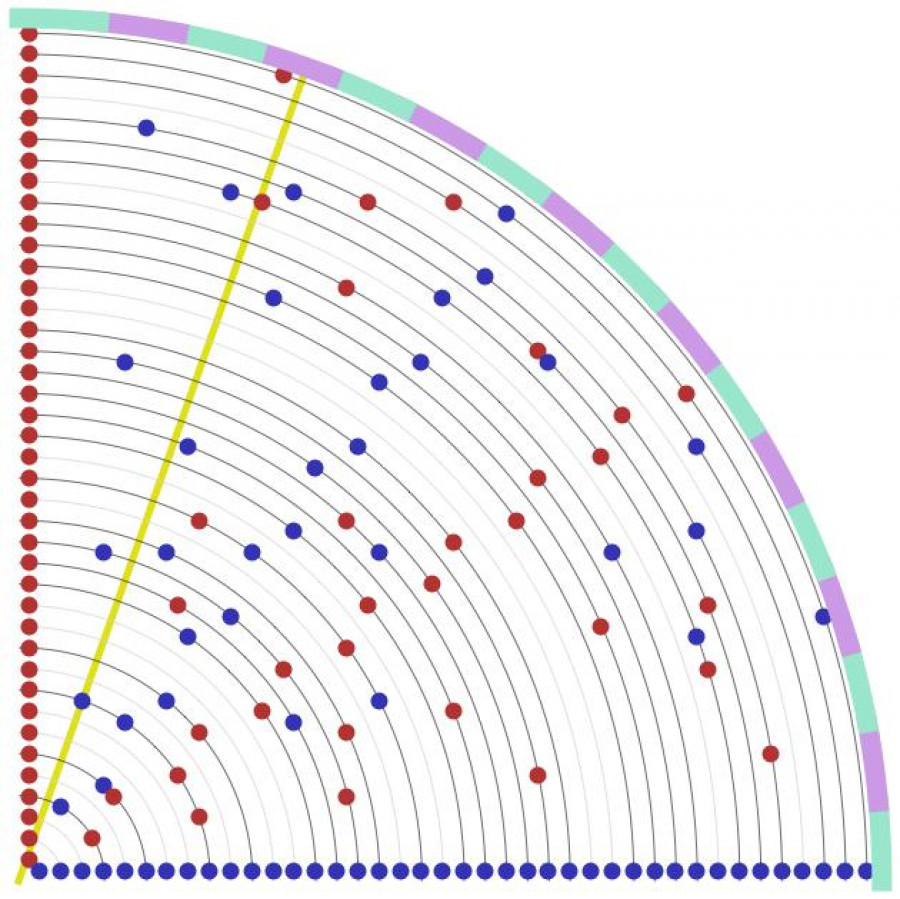
Abychom z toho hyperboloidu vytřískali nějaké zvuky, musíme každému takovému netriviálnímu modrému bodu přiřadit tón o určité výšce a délce. To uděláme takto:
Nejprve si na okraji našeho obrázku vytvoříme stínítko, rozdělíme ho na malé chlívky (obarvené světle zeleně a fialově) a každému chlívku přiřadíme určitý tón. No a pak každý modrý bod prostě promítneme z počátku na stínítko (to je ta žlutá čára) a z tabulky tónů, kterou si držíme někde v počítači, vyčteme výšku. Pokud se v nějaké letové hladině setkají dva či více modrých bodů, tak z nich prostě sestavíme akord.
Co se délky tónu (nebo akordu) týče, tu odvodíme takto. Z obrázku je vidět, že ne každá letová hladina obsahuje netriviální modrý bod. Některé letové hladiny jsou prázdné a obsahují pouze triviální body (odpovídající kružnice jsem udělal hodně světle šedé). Délka tónu bude určena vzdáleností od předchozí „netriviální hladiny“. Tedy čím větší „díra“ před danou letovou hladinou, tím delší tón. Na obrázku např. uvažuji bod (6, 17, 18), který leží v letové hladině 18. Před ním jsou ale dvě prázdné letové hladiny (14 a 16), takže délka tónu bude trojnásobkem základní délky (kterou si zvolíte libovolně, podle toho, zda chcete získat cajdák anebo kvapík). Ta základní délka samozřejmě odpovídá rozdílu 2. Bereme pouze sudé letové hladiny, takže menší rozdíl nepořídíme.
Protože z obrázku nejsou letové hladiny moc dobře vidět, tady je výčet prvních netriviálních modrých bodů našeho hyperboloidu (levý sloupec). V pravém najdete obdobné body pro jiný hyperboloid, pokud chcete experimentovat (body zde pro jednoduchost značím x.y a rovnítko znamená stejnou letovou hladinu).
Z levého sloupce vidíte, že existují tři letové hladiny (18, 32 a 38), které nám vygenerují dvojtón. Ve vyšších letových hladinách ale lehce najdeme kombinaci tří a více tónů.
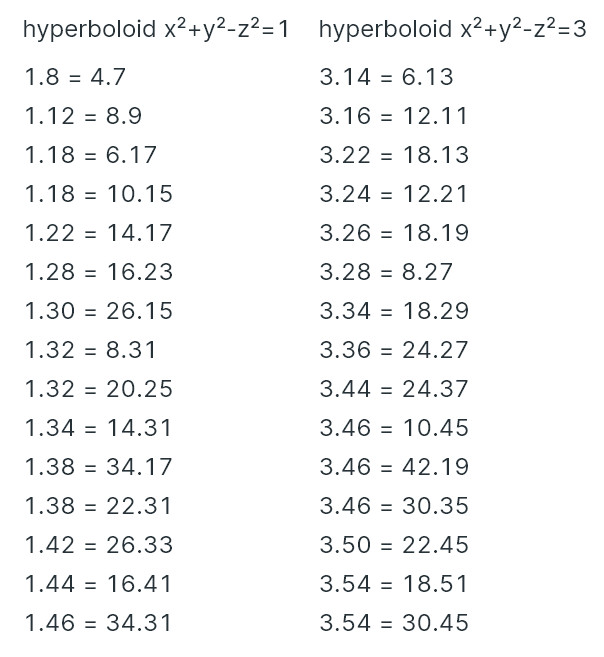
Pokud vás zajímají krvavé detaily, pak vězte, že počet netriviálních řešení v dané letové hladině souvisí s rozkladem komplexního čísla z + i na prvočinitele. Například v 8. hladině rozložíme číslo 8 + i na (1 + 2i) * (2 - 3i). Teď jeden z těch faktorů přehodíme na komplexně sdružený a celé to roznásobíme: (1 + 2i) * (2 + 3i) = -4 + 7i. Rozmyslete si, že obě komplexní čísla musí ležet na stejné kružnici (se středem v počátku). A vzhledem k tomu, že se zajímáme pouze o 1. kvadrant, vezmeme výsledek v absolutní hodnotě a dostaneme kýžený bod (4,7) – tedy v tabulce označený 4.7. Samozřejmě čím vyšší letová hladina, tím vyšší pravděpodobnost, že naše komplexní číslo bude mít hodně prvočinitelů a vzniklá hudba bude tudíž mít dostatek akordů). Ty prázdné letové hladiny (šedé) odpovídají komplexním prvočíslům, např. 2 + i, 4 + i, 6 + i, 10 + i, 14 + i, 16 + i, 20 + i atd. Tato čísla se rozložit nedají.
V praxi ale není nutno si s komplexní analýzou lámat hlavu. Z tabulky je vidět, že součet čtverců u každé rovnosti je stejný, takže třeba na prvním řádku stačí najít celočíselné řešení úlohy 12 + 82 = x2 +y2 a to počítač zvládne metodou pokusů a omylů za zlomek vteřiny (platí totiž že x a y musí být obě menší než z, takže si uděláte dvě smyčky od 1 do z a projedete v x a y všechny možnosti).
V první ukázce níže jsem to zeleno-fialové stínítko osídlil chromatickou stupnicí (c-cis-d-dis-e-f-fis atd) zhruba přes tři oktávy, takže to, co dostaneme, bude harmonicky poněkud neukotvené. Bude to znít tak trochu jako Béla Bartók po osmém pivu. Ale jako nástroj jsem vybral xylofon, který je v MIDI provedení (to je formát na záznam hudby) celkem snesitelný. Začneme v letové hladině 1100 a odtud pojedeme nahoru.
Ve druhé ukázce víceméně zopakuji tu první s tím rozdílem, že chromatickou stupnici vyměním za E dur a malinko zpomalím tempo. A začneme podstatně níž – na letové hladině 300.
A to je z muzikomatiky všechno. Vlastně ne. Na jeden zvuk jsem úplně zapomněl.
Zazvonil zvonec a Matykání byl konec.
Cink.
Pokud vás ještě nebolí hlava, tak tady jsou toho randálu čtyři minuty...
Článek je redakčně upravenou verzí blogového příspěvku na serveru iDNES.cz. Publikováno s laskavým svolením autora. Další díly a původní texty jsou dostupné na blogu Jana Řeháčka.