Zajímá vás, jaké barvy se letos budou nosit v komplexní rovině? Přemýšlíte, jaký střih zvolit pro kacabajku z hyperbolických kosinů? Nevíte, jaký je ten správný doplněk k množině všech kořenů? Nuže vstupte, jste na správné adrese.

První imaginární módní přehlídku popsal Hans Christian Andersen ve známé pohádce Císařovy nové šaty. Jak dopadla, všichni dobře víme: kde nic není, ani čert (natož matematik) nebere. Zlé jazyky dokonce tvrdí, že v závěru musela zasahovat dánská mravnostní policie. Abych se tedy nedostal do křížku se zákonem, podíváme se dnes na jiný typ imaginární garderoby - na grafy komplexních funkcí.

O tom, že komplexní funkce dokáží být zdrojem nevšedního estetického zážitku, svědčí například fraktály, jejichž nejznámější ukázky se dají vytvořit jejich iterací. V tomto článku se vás pokusím přesvědčit, že i prostý graf komplexní funkce dokáže pošimrat vaše umělecké alter ego, pokud se správně zobrazí.

Já vím, jen stěží si lze představit, že by na střední škole nějaká frekventantka vzdychla: „Jé, holky, koukněte se na tu sinusoidu, tu bych chtěla mít na šatech!“ Ale to je proto, že funkce probírané na gymnáziu jsou v podstatě jednorozměrné a na reálné ose se z jejich chování moc zázraků vykouzlit nedá. V komplexní rovině má matička Estetika podstatně víc příležitostí k elegantním kreacím.

V první části tohoto příspěvku vám ukážu několik způsobů, jak si můžete komplexní funkce vizuálně představit, a potom se podíváme na pár ukázek techniky zvané „barvení definičního oboru“ (domain coloring) v těch nejživějších odstínech.

Znázornění komplexních funkcí

Zobrazení reálných funkcí nepředstavuje žádný problém. Nezávisle proměnná (vstup) na jednu osu, závisle proměnná (výstup) na druhou a než bys řekl švec, máme tradiční graf v rovině x-y. Komplexní čísla jsou ovšem sama o sobě body v rovině, takže na analogický „obrázek“ bychom potřebovali čtyři souřadné osy - dvě na vstupní rovinu a dvě na výstupní. S trochou nadsázky by se dalo říci, že pokud si dokážete představit komplexní funkci, jste na nejlepší cestě k pochopení čtyřrozměrného prostoru.

To je pro běžného smrtelníka žijícího ve třech dimenzích vážný problém, a tak si matematici postupem času vyvinuli několik metod, jak čtyřrozměrné zobrazení obejít - tak aby jim oči nešly šejdrem, ale mozek získal jakous takous představu, jak ty komplexní funkce vlastně fungují.

Začneme nejjednodušší variantou. Čtyřrozměrný obrázek rozdělíme na dva trojrozměrné (3D).

Komplexní funkce w = f(z) je de facto formulka, která vstupnímu komplexnímu číslu z přiřadí výstupní číslo w. Vstupní komplexní proměnnou z zobrazíme v tradiční rovině x-y a na svislou osu obou 3D obrázků pak pro každé z vykreslíme dvě souřadnice, které určují výstupní hodnotu w. V prvním komplexním Matykání jsme viděli, že souřadnice se dají zavést dvěma způsoby. Buď použijeme kartézský systém (tedy tradiční x a y), anebo polární (úhel a poloměr) - viz první obrázek.

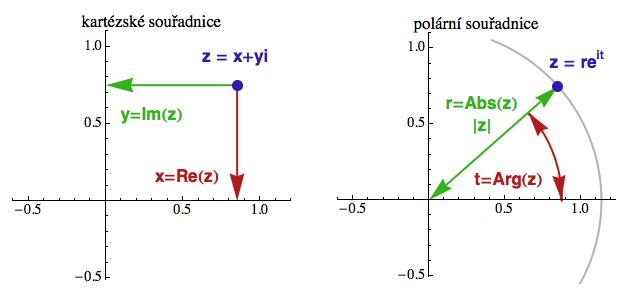
Jako první si na trojrozměrný paškál vezmeme souřadnice kartézské. Těm se v komplexní hantýrce místo x a y říká reálná a imaginární část (komplexního čísla).

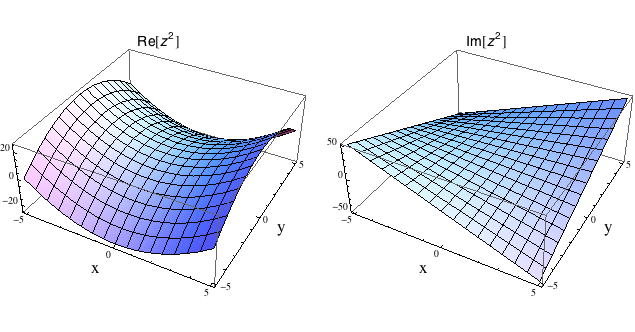
Na dalším obrázku je graf komplexní funkce w = z² s tím, že nalevo vidíme na svislé ose reálnou složku výstupní hodnoty Re[w] a napravo složku imaginární Im[w]. U takto jednoduché funkce můžeme komponenty přímo spočítat a dostaneme w = z² = (x+iy)² = x² - y² + 2xyi. Pokud dobře ovládáte funkce dvou (reálných) proměnných, můžete si tedy reálnou složku představit jako f(x,y) = x² - y² a imaginární jako g(x,y) = 2xy. Výsledný 4D obraz komplexní funkce si samozřejmě musíte složit sami ve své vlastní představivosti.

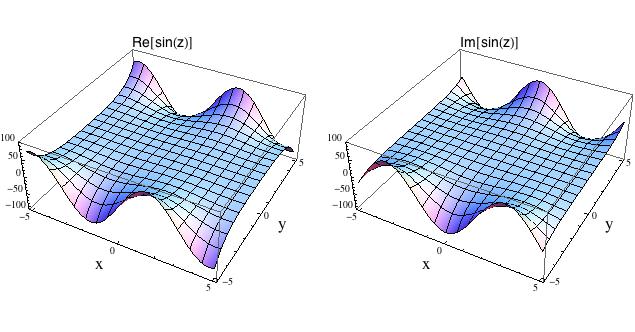
Na dalším obrázku je totéž pro funkci w = sin(z). Její graf je sice charakteristicky zvlněný, ale když budete na reálné ose (y = 0) hledat tradiční sinusoidu, neuvidíte ji, protože její kmitání mezi -1 a 1 je v měřítku svislé osy takřka nepostřehnutelné. V komplexních číslech se sinusoida dokáže vybudit k podstatně větším hodnotám, takže její tradiční vlnky v reálných číslech působí jako taková tintítka.

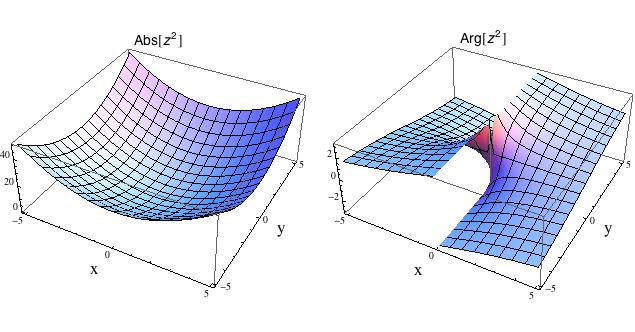
A teď zkusíme rozdvojení pohledu s polárními souřadnicemi. V rovině x-y si opět vybereme nějaký vstup z = x + iy a na svislou osu obou obrázků tentokrát vyneseme polární souřadnice výstupní proměnné w. Nalevo vykreslíme polární poloměr Abs[w] a napravo polární úhel Arg[z] pro funkci w = z².

Vidíte, že úhel je jakoby „přetržený“. To není proto, že by funkce byla nespojitá, ale proto, že nespojitý je sám úhel. Pokud si představíte, že pochodujete podél jednotkové kružnice a zaznamenáváte si svou polohu pomocí úhlu sevřeného v počátku, tak v jistém okamžiku budete muset „skočit“ z 360 zpátky do 0 (měřeno ve stupních). Taková je bohužel povaha úhlové míry.

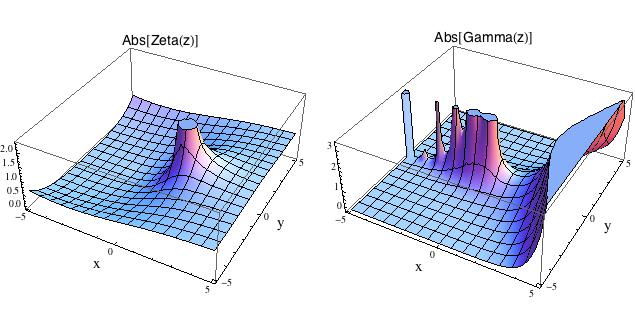
V mnoha případech nám ale stačí, když pochopíme alespoň absolutní hodnotu na výstupu z naší funkce. Na další dvojici obrázků je tato znázorněna (již bez úhlu) pro dvě vyšší funkce: zeta a gama (viz Matykání o kořenech). U funkce zeta je patrný pól v bodě z = 1. U funkce gama si všimněte, jak rychle pro x > 0 roste. Je to koneckonců spojitá verze faktoriálu (komínky vlevo odpovídají pólům v záporných číslech).

Nespojitost ve znázornění úhlu se ale matematikům moc nelíbila, a tak si na to konto koncem 90. let vymysleli báječnou vychytávku. Někdo si povšiml, že v grafických programech se často používá tzv. barevné kolo (color wheel), které má tu skvělou vlastnost, že zobrazuje úhly na barvy spojitě. Jinými slovy, když si projdete těch 360 stupňů, tak jste zcela bezbolestně zpátky ve stejné barvě a nemusíte skákat z hodnoty 360° do 0°.

Takže my si ten polární úhel Arg[z] můžeme znázornit tak, že příslušný pixel sedící v bodě z = x + iy obarvíme barvou, která odpovídá úhlu výstupní proměnné w. A žádnou svislou osu, na kterou bychom museli tlačit stupně nebo radiány nebudeme vůbec potřebovat.

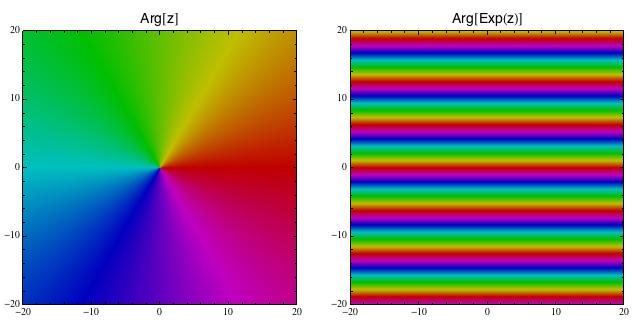
Na dalším obrázku vlevo je to znázorněno pro nejjednodušší funkci a to je w = z. Výstupní w je tedy to samé, co vstupní z, a to znamená, že všechny polopřímky vycházející z počátku budou mít stejnou barvu (protože body na těch polopřímkách sedící mají stejný polární úhel).

Na obrázku vpravo je totéž pro funkci w = exp(z). Z minulého Matykání vyplynulo, že komplexní exponenciála má tvar exp(x + iy) = exp(x).exp(iy), což naznačuje, že všechny vstupní body ležící na jakékoliv horizontální přímce (s konstantním y) se zobrazí na komplexní číslo se stejným úhlem. Proto je na obrázku každá horizontální přímka obarvená jen jednou barvou.

Většina grafů níže bude založena na tomto principu. Pokud je chcete opravdu pochopit, dobře si předchozí pasáž rozmyslete.

Polární úhel je ale pouze polovina informace o výstupní proměnné. Samozřejmě že bychom barevné obrázky obsahující informaci o chování Arg[f(z)] mohli doplnit o grafíky absolutní hodnoty Abs[f(z)] (a dostat tak dvojobrázek - obdobně jako pro kartézské souřadnice). Matematici se však neradi dívají na dva obrázky současně, a tak se rozhodli informaci o chování absolutní hodnoty vpašovat do barevných schémat pomocí šrafování, které bude indikovat (obvykle na logaritmické škále), jak absolutní hodnota stoupá.

Ovšem pozor, šrafování budeme muset periodicky vynulovat, jinak by nám obrázek velmi rychle „zčernal“. Nejlépe si ho můžete představit jako vrstevnice. Když je protínáte, absolutní hodnota stoupá (či klesá), pokud se pohybujete „podél“ nich, absolutní hodnota na výstupu bude zhruba stejná.

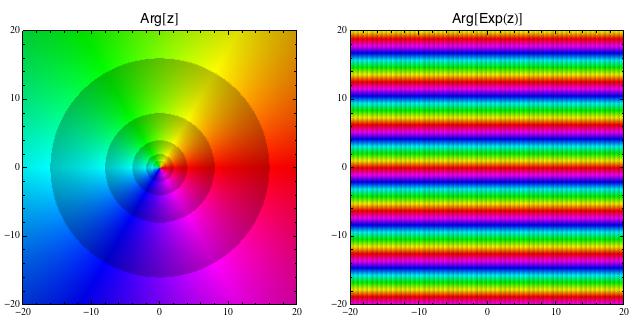
Na obrázku vlevo vidíte šrafování opět pro funkci w = z, kde absolutní hodnota stoupá podél paprsků z počátku (na každé kružnici se středem v počátku je absolutní hodnota konstantní). Vpravo je totéž pro funkci w = exp(z) a tady je absolutní hodnota konstantní pro každé pevné x (člen obsahující y totiž leží na jednotkové kružnici, takže jeho absolutní hodnota je 1). Také si všimněte, že šrafování je v podstatě vertikální (Abs(w) tedy stoupá, pohybujeme-li se podél osy x).

Než se podíváme na vlastní módní přehlídku, chci vám ukázat ještě jeden způsob zobrazování komplexních funkcí. Místo, abychom výstupní hodnoty w roztrhli na dvě souřadnice a vykreslili každou odděleně, pokusíme se pochopit způsob, jakým naše komplexní funkce zobrazuje vstupy na výstupy.

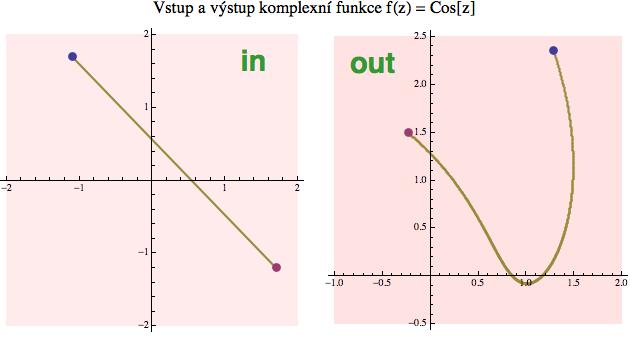
Za tím účelem si vytvoříme dvě kopie komplexní roviny - jednu pro vstupy (in) a jednu pro výstupy (out). A teď si v té vstupní vybereme nějaké body z (třeba ten modrý a červený), hodíme je do funkce a to, co nám z ní vyleze - tedy výstupní hodnoty w - zobrazíme ve výstupní rovině.

Ale protože dělat to jen pro individuální body nám toho moc nepoví, můžeme si vzít nějaký geometrický útvar - např. úsečku mezi těmito body - a také jej hezky bod po bodu pomocí naší funkce zobrazit.

Tento trik nám sice dává celkem zajímavou informaci o tom, jak naše funkce páruje vstupy a výstupy, ale je potřeba do toho vnést trochu pořádek. Tedy nebrat si jen tak nějakou úsečku mezi dvěma náhodně zvolenými body, ale postupovat systematicky.

Vybereme si několik úseček podél souřadnicových os (a můžeme je klidně barevně odlišit) a ty pak opět bodu po bodu zobrazíme do výstupní roviny pomocí naší komplexní funkce. Na obrázku níže je to provedeno pro náhodně vybranou kubickou funkci.

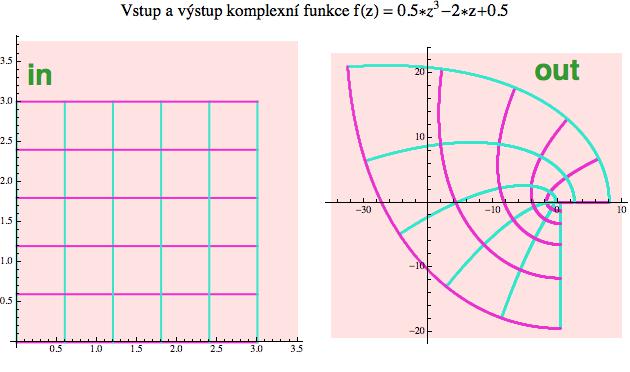
Takový diagram nám ukáže, jak funkce f(z) v komplexní rovině operuje.

V obrázcích níže budu používat převážně šrafované polární „barvičky“, ale pro lepší orientaci do toho občas přimíchám pár zobrazení souřadnicových úseček (nechám je ovšem tenoulinké, aby se moc netloukly s tím šrafováním).

Imaginární módní přehlídka

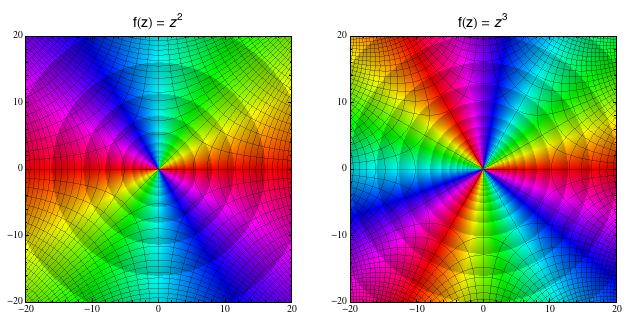
Prohlídku podzimní kolekce začneme jednoduchými mocninami. Na rozdíl od funkce f(z) = z se tady ty barvy prostřídají dvakrát, resp. třikrát. To je proto, že funkce f(z) = z² zdvojnásobuje úhly: napište si polární formu z = r.exp(it), umocněte ji na druhou a podívejte se, co to udělalo s téčkem (zdvojilo ho to). Tím pádem tam, kde vstupní proměnná z proběhne úhel od 0° do 360°, výstupní w se protočí od 0° do 720°. No a v té kubické funkci se barvy ze stejného důvodu protočí třikrát.

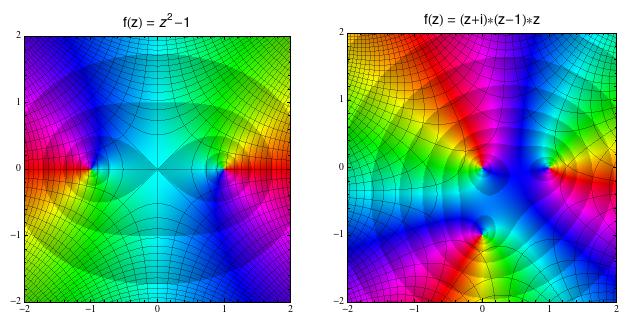
Předchozí dvojice obrázků je trochu nudná, protože obě mocniny mají kořeny v nule (a nikde jinde). Na dalším dvojobrázku uvidíte polynomy, které mají kořeny různě rozseté po komplexní rovině. Ten vlevo je má v bodě 1 a -1, ten vpravo v bodech 1, -i a 0 (když se pozorně podíváte, tak je naleznete).

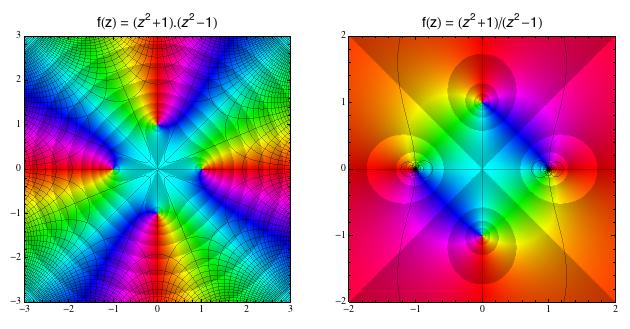
Na dalším obrázku se podíváme na rozdíl mezi kořeny (kde je f(z) rovna nule) a póly (kde je f(z) rovno nekonečnu). Vzal jsem si dva kvadratické polynomy a vlevo vykreslil jejich součin, vpravo jejich podíl. Součin má 4 kořeny (1, -1 , i, -i), zatímco podíl má dva kořeny (i, -i) a dva póly (1, -1).

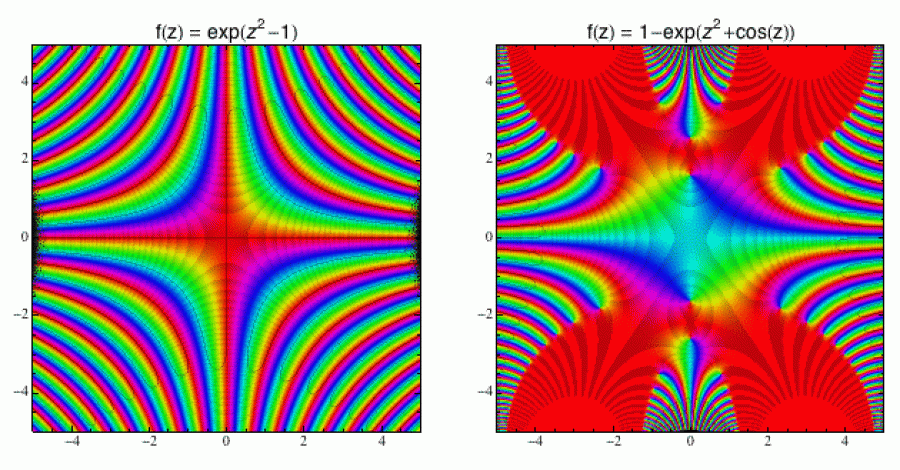
Exponenciálu jsme viděli nahoře - ta sama o sobě moc zajímavá není - ale pokud do ní ještě nacpete nějaký kvadratický člen (nebo dokonce kosinus), tak se i ona v komplexní rovině ráda rozdovádí.

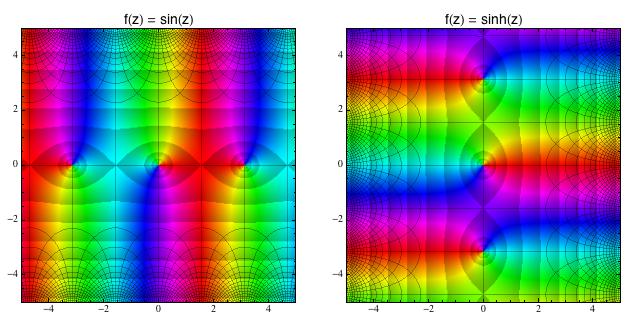
Další pán na holení bude sinus a jeho hyperbolický bratr sinh(z). V minulém Matykání jsem vám ukázal, že v komplexní rovině je sinus a hyperbolický sinus prakticky ta samá funkce (akorát překlopená o 90°) a z obrázku dole to celkem lehce vidíte. Klasickou periodicitu sinu vidíte vlevo podél osy x („oční“ vzorek se tam opakuje s periodou 2π).

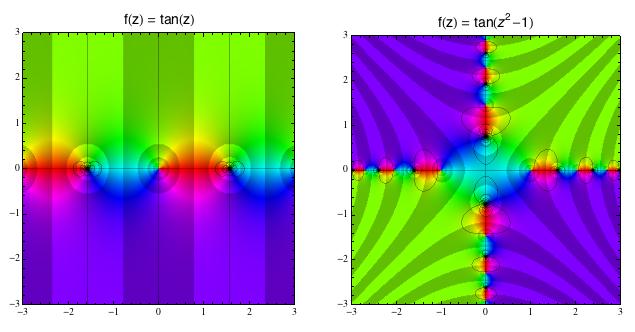
Dále vám nabídnu tangens, který je podílem sinu a kosinu. A pokud je vám to málo, vyšperkoval jsem ho v pravé části opět malým kvadratickým členem.

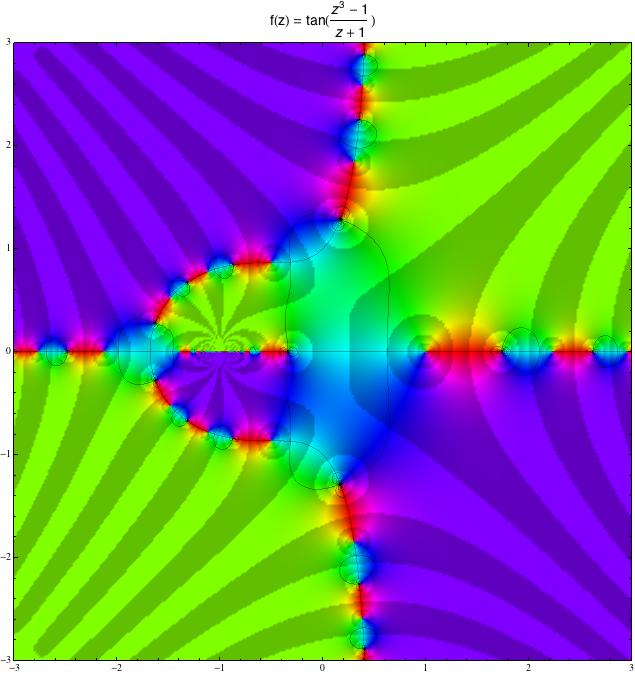
Pokud do tangensu narvete racionální funkci (tj. podíl polynomů), podaří se vám vykouzlit už celkem zajímavé umělecké dílko.

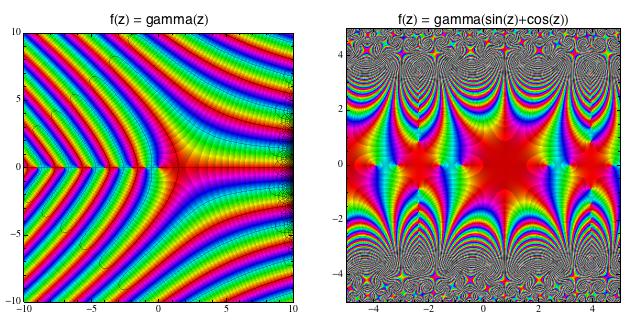
Tak a teď vzhůru na vyšší funkce. Gama je sice celkem fádní, ale když do ní „přisypete“ sinus a kosinus, tak umělecky trochu „prokoukne“.

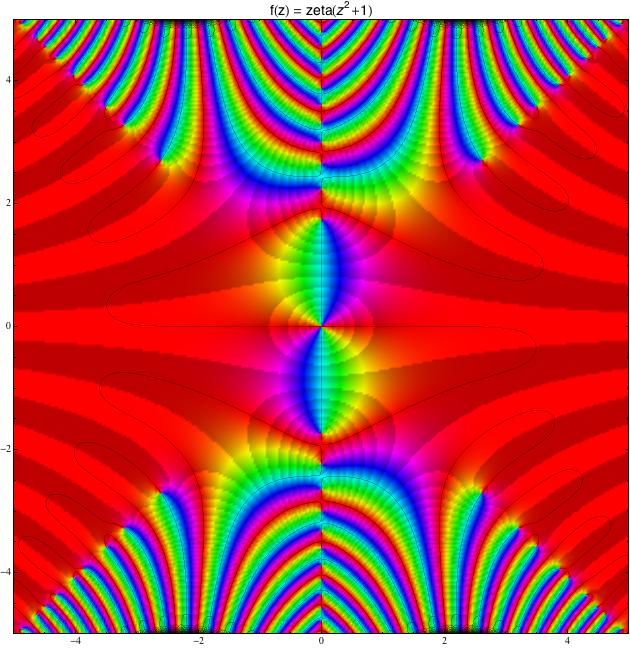
To funkce zeta je zajímavá sama o sobě (pro ni vám ukážu trochu větší kus komplexní roviny). Ten čudlík uprostřed odpovídá jejímu pólu v bodě z = 1 a konce barevných jazyků odpovídají tzv. netriviálním kořenům (o nich bude přespříští Matykání).

I tetička Zeta však vypadá pohledněji, když do ní strčíme nějaký ten polynom.

Asi jste už zjistili, že obecně platí, že čím složitější funkce, tím zajímavější a členitější její „polární graf“ je. Proto jsem pro vás na závěr vybral exponenciálu, do které jsem narval součet kosinu a kvadrátu, a ještě jsem to celé vydělil zetkem - ať nežeru.

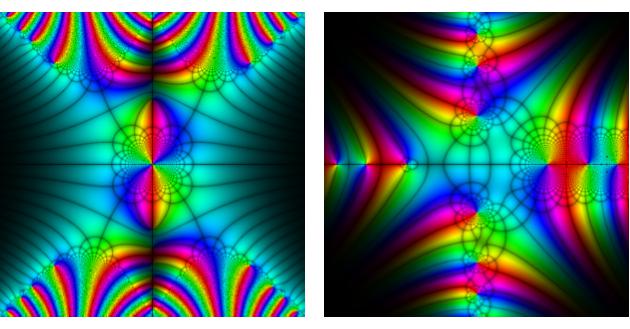
Pokud vás takovýto způsob zobrazení komplexních funkcí zaujal (nebo se ho dokonce chystáte využít v oboru módního návrhářství), doporučuji juknout na Wikipedii a zejména si pročíst externí linky uvedené v závěru (já jsem použil software Mathematica - podrobnosti zde nebo zde nebo zde). Ty algoritmy na barevné provedení polárního úhlu i znázornění absolutní hodnoty se trochu mění. Pokud použijete první „zde“, dostanete zhruba tento typ obrázků: