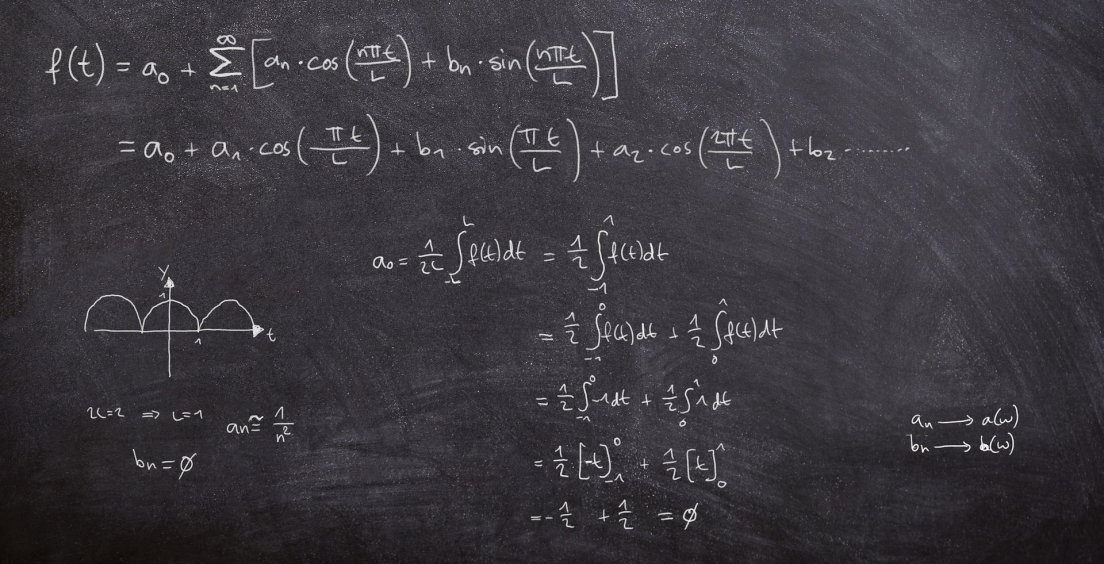Diferenciální rovnice. Co o nich v perexu říci? Dvakrát měř, jednou řeš. Kdo chce čtverec odmocnit, kalkulačku si vždy najde. Kam čert nemůže, nastrčí integrál. Důkaz má krátké nohy. Lepší skalár v hrsti, nežli vektor na střeše.
Již od dob, kdy první pračlověk promokl v nečekaném pralijáku a z jeho mamutí prapaštiky se stal nepoživatelný rosol, bylo našim předkům jasné, že je nutno naučit se předvídat dění na obloze. Tím spíš, když se z rozkládajícího se rosolu stal zapáchající aerosol.
Zpočátku rozpracoval první prameteorolog pouze vizuální metodiku: mrak = zůstat v jeskyni, sluníčko = vyrazit na lov či sběr, popřípadě na zkvašené přesličky se sousedem Kopčemem. Protože se ale validita takové předpovědi pohybovala v řádu hodin, postupně se člověk naučil odpozorovávat sekundární indikátory od živočichů, kterým matička příroda nadělila do vínku o něco více meteorologického talentu. Nenápadně sledoval chování rosniček, rozlezlost mravenců či výšku letu vlaštovek a trpělivě skládal mozaiku poznání. Člověk je tvor zvídavý a má poměrně dobrého pamatováka, takže nebyl problém korelovat tyto poznatky s dalšími indikátory počasí jako formace oblaků, mizení rosy či dokonce bolesti v kloubech. Protože ale v této době (mluvíme o době předinternetové) žádný prafejsbuk neexistoval, naučil se přenášet pracně nasbírané zkušenosti z jedné generace na druhou prostřednictvím lidových pranostik:
Na Hromnice musí skřivan vrznout, i kdyby měl zmrznout.
Některé poskytovaly až udivující numerickou přesnost.
Medardova kápě čtyřicet dní kape.
Jiné zase přesahovaly do oboru ekonomických prognostik.
Studený máj v stodole ráj.
Kvalitativní zkušenosti nás ve vnímání atmosférických procesů sice o kousek posunuly, ale na úsvitu moderní doby bylo jasné, že se neobejdeme bez kvantitativního přeměřování. A nastala doba přístrojová. Barometry, tlakometry, teploměry, anemoskopy, vlhkoměry, a později i radary a družice postavily meteorologii a modelování počasí na solidní experimentální základ. A jak jsme se naučili přesněji měřit i čas, v lidových pranostikách se objevily první známky chronologických modelů:
Na Nový rok o slepičí krok, na Tři krále o krok dále, na rovnice o hodinu více.
Jen chudáci naši předkové netušili, že se bude jednat o hodinu matematiky. Tak se do ní rovnou vrhneme. Inu, kdo rychle derivuje, dvakrát derivuje.
Prebambule přeskočitelná
Rovnice je taková... jak bych to řekl... zlý nehezký ošklivá věc. Ale plave v ní naše oblíbené písmenko x, a tak ho volky nevolky zachráníme.
Typů rovnic je mnoho a abychom si to moc nekomplikovali, předpokládejme, že na pravé straně máme číslo č a na levé nějaký algebraický chuchvalec obsahující x. Budeme ho reprezentovat funkcí f.
f(x) = č
Ve škole se naučíme to x z chuchvalce různými speciálními postupy vysekat, ale z abstraktního pohledu se na (skoro) všechny dílčí metody můžeme dívat tak, že na obě strany rovnice provedeme inverzní funkci (budu ji značit f ̄)
x = f ̄(f(x)) = f ̄(č)
Tím je x vysvobozeno a jeho hodnota se skví přímo před našima očima.
Podívejme se na konkrétní příklad:
3 = x2 - 1
Naše funkce f(x) = x2 - 1 je složením dvou funkcí f(x) = h(g(x)), kde
g(x) = x2 a h(x) = x-1
Rovnici vyřešíme tak, že k oběma stranám přičteme 1 (což je de facto inverzní funkce k h) a pak odmocníme (což je více méně inverzní funkce ke g). Takže:
4 = x2
2 = x
Já vím, s těmi odmocninami je to trochu komplikovanější, ale s nějakým plus – minus si teď nelámejme hlavu.
Inverzní funkce jsou tedy jakási kladívka, pomocí kterých rozbíjíme ten algebraický chuchvalec, ve kterém zoufale trčí naše milované x. Inu, inverzní funkce melou pomalu, ale jistě.
Jak asi tušíte, věc uvězněná v algebraickém chuchvalci může být i něco komplikovanějšího než jen pouhá skalární veličina. Například celá funkce. Budeme-li třeba hledat neznámou funkci f(x), splňující rovnici
3-exp(f(x)) = 2 - 5x
budeme prostě do té rovnice klepat různými kladívky, až z ní vyklepáme
exp(f(x)) = 1 + 5x
a protože inverzí exponenciály je logaritmus, máme:
f(x) = ln(1 + 5x)
Tohle byla zatím jen variace na předchozí téma s tím, že se z chuchvalce snažíme vysvobodit celou funkci f(x) a na x se díváme jen jako na kompars, tedy na něco, s čím nakládáme jako s ostatními konstantami.
Funkce jsou ale komplikovanější objekty a mohou do rovnice vstupovat pro různé hodnoty své proměnné (k takové politováníhodné události u čísel pochopitelně nedochází). Například známá Cauchyova funkční rovnice se ptá na funkce splňující vztah
f(x + y) = f(x) + f(y)
Pro racionální čísla se dá ukázat, že řešením – jak očekáváme – jsou lineární funkce f(x) = cx, kde c je racionální konstanta. Pro reálná čísla x je ale situace podstatně komplikovanější a vede k zajímavému pojmu Hamelových bází (které se snaží reálná čísla rozložit na racionální kombinace určitých bázových čísel).
Tento typ rovnic představuje poměrně esoterickou a málo známou podoblast matematiky: funkční rovnice. V nich se kromě nezávislé proměnné vyskytují pouze známé a neznámé funkce (v příkladu nahoře byla neznámá funkce f(x) a známá funkce exponenciála). Asi nejproslulejší takovou rovnicí je Riemannova funkční rovnice, která umožňuje výpočet hodnot funkce zeta.
Ještě zajímavější je situace, kdy se v rovnicích kromě neznámých funkcí motají také jejich derivace. Těm říkáme diferenciální a o nich bude zbytek tohoto Matykání.
V úvodu jsme si řekli, že algebraické rovnice se většinou řeší aplikací inverzních funkcí (což je pouze trochu abstraktnější pohled na běžné středoškolské postupy). A protože inverzní operací k derivování je integrování, nemělo by nás překvapit, že diferenciální rovnice se řeší integrací (byť občas dovedně zamaskovanou). Inu, co se v algebře naučíš, v kalkulu jako když najdeš.
Diferenciální rovnice
Aby nám v rovnicích nevrávoralo moc písmenek, budeme funkci značit stejným písmenkem jako závisle proměnnou, tedy y (z kontextu bude jasné, zda myslíme funkční hodnotu nebo přímo funkci jako takovou).
Místo y = f(x) budeme tedy hledat funkci y = y(x).
A jak taková diferenciální rovnice vypadá? Třeba takhle:
y' + 2xy = 0 neboli y' = -2xy
což v nezkráceném zápisu znamená, že hledáme neznámou funkci y(x), která splňuje rovnici
y'(x) = -2x * y(x)
(její derivace v každém bodě se rovná minus dvojnásobku součinu argumentu a funkční hodnoty)
Abychom nezačali zhurta, podívejme se na jednodušší typ, který se dá vyřešit prostou integrací.
y' = -2x
Tady je funkce na pravé straně zadaná explicitně, takže prostě hledáme funkci, jejíž derivace je 2x. To je dle definice přesně primitivní funkce (neboli antiderivace neboli integrál neurčitý). A ta se buď vyhledá v tabulkách anebo spočítá z integračních vzorečků (které jsou v jistém smyslu obrácením derivačních vzorečků). Zde dostaneme
y(x) = -x2 + C
(kde C je integrační konstanta, kterou přidáváme ke každé antiderivaci,
protože všechny konstanty se zderivují na nulu a my chceme mít co
nejobecnější zápis, aby nám žádná funkce řešící naši rovnici
neunikla).
A ještě bych poznamenal, že my zde de facto integrujeme obě strany s tím, že nalevo dostaneme triviálně y(x). Abychom mechaniku tohoto procesu dostali do ruky, podívejme se na to podrobněji. Derivaci vyjádříme jako formální podíl diferenciálů (nebojte, diferenciály nekoušou, zde jsou to v podstatě jen mnemotechnické pomůcky pro zápis integrálů) a dostaneme
dy / dx = -2x
Teď pronásobíme obě strany diferenciálem dx
dy = -2x dx
a obě strany zintegrujeme:
∫ 1 dy = ∫ -2x dx
Vyjdou nám primitivní funkce: primitivní funkce -2x je -x2 a primitivní funkce k 1 je y (protože dy nám říká, že pracujeme s proměnnou y).
y + C = -x2 + D
a abychom se nemuseli tahat se dvěma libovolnými konstantami, sloučíme je v jednu
y = -x2 + C
Vidíte tedy, že diferenciály žádnou velkou roli nehrály, pouze nám registrují, podle jaké proměnné zrovna provádíme integraci.
A teď k původní rovnici y' = -2xy.
Tady už pravou stranu přímo integrovat nemůžeme, protože v ní stále překáží hledaná (a neznámá) funkce y(x). Za jistých okolností (a tady zrovna nastanou), ale můžeme závisle a nezávisle proměnnou algebraicky odseparovat – tedy naházet x na jednu stranu rovnice a y na druhou – a integrovat pak opět obě strany podle jejich proměnných (jako nahoře). Jen musíme dávat pozor, abychom si při manipulaci nestrčili diferenciály omylem do jmenovatele, protože pak by neurčitý integrál nedával smysl.
Takže začneme opět tak, že derivaci přepíšeme jako podíl diferenciálů.
dy/dx = -2xy
a separujeme (držíce diferenciály „nahoře“)
dy / y = -2x dx
Kdybychom diferenciály šoupli dolů, vypadalo by to takto
- 1 / 2xdx = y / dy
a takový výraz se integrovat nedá. Ten předchozí ano:
ln(y) = -x2 + C
y = exp(-x2) * K
(kde K je exp(C))
a řešením jsou kladné násobky funkce exp(-x2).
Diferenciální rovnice tedy mají nekonečně mnoho řešení. Abychom z nich dostali pouze jedno, musíme ještě na hledanou funkci y(x) uvalit dodatečnou podmínku, která většinou (ale ne vždy) specifikuje hodnotu funkce v nule (proto se jí říká počáteční podmínka): tedy např. y(0) = 2 (na obrázku vpravo vyznačena zeleně).
Pojďme ho najít. Když si do předchozího obecného řešení dosadíme x = 0, dostaneme
y(0) = exp(0) * K
a tedy
2 = 1 * K
a funkce splňující naši diferenciální rovnici se zelenou počáteční podmínkou bude odpovídat hodnotě K=2. y(x) = 2 * exp(-x2)
Pochopitelně ne každá diferenciální rovnice se dá separovat, proto se občas musí nasadit přibližné numerické metody – ale o tom až za chvíli. Inu, čiň čertu dobře, numerickými metodami se ti odmění.
Před časem jsme viděli, že existují i derivace vyšších řádů a i ty se mohou v diferenciálních rovnicích vyskytovat. Např. Newtonův zákon obsahuje zrychlení, což je druhá derivace polohy podle času (první derivace je rychlost), takže velmi často najdeme rovnice obsahující druhé derivace v klasické mechanice.
Jako příklad se podívejme na tzv. lineární rovnici druhého řádu (nalevo je lineární kombinace funkce a jejích derivací).
y'' - 4y = 0 neboli y'' = 4y
(hledáme zde funkci, jejíž druhá derivace je čtyřnásobek funkční
hodnoty)
Tento typ rovnic se opírá o známou skutečnost, že exponenciála je vůči derivaci imunní, a pokud do ní ještě vložíme konstantu, je skoro imunní:
(exp(kx))' = k exp(kx)
což z pohledu integrování znamená
∫ exp(kx) dx = exp(kx) / k
A tato vlastnost exponenciály nám umožní převést integraci na algebraický problém.
Zkusme tedy hledat řešení rovnice y'' - 4y = 0 ve tvaru
y(x) = exp(kx)
s tím, že zatím neznámou konstantu k zvolíme tak, aby rovnice „vyšla“ (což je pro tento typ rovnic možné díky zmíněné „imunitě“).
Když si spočítáme druhou derivaci takto zvolené funkce, obdržíme:
y'' = k2 exp(kx)
a dosazením funkce i druhé derivace (v tomto tvaru) do rovnice nám dá:
k2 exp(kx) - 4 exp(kx) = 0
Exponenciála je vždy kladná, takže ji můžeme zkrátit, aniž by nám hrozilo dělení nulou.
k2 - 4 = 0
a to je snadná kvadratická rovnice s řešením k = 2 a k = -2
Dvě konkrétní řešení naší rovnice jsou tedy exp(2x) a exp(-2x) a obecné řešení pak dostaneme jejich lineární kombinací.
y(x) = A exp(2x) + B exp(-2x)
Takových funkcí je mnoho a abychom z nich dostali jednoznačné řešení, potřebovali bychom dvě počáteční podmínky, protože máme v obecném řešení dvě neznámé konstanty. Například bychom mohli zadat funkci ve dvou různých bodech:
y(0) = 1 a y(1) = 2
anebo zadat funkci PLUS derivaci v jednom bodě
y(0) = 1 a y'(0) = 2.
S druhou možností se opět velmi často setkáváme ve fyzice, protože abychom mohli studovat pohyb bodu v nějakém silovém poli, musíme znát nejen počáteční polohu, ale také počáteční rychlost. Inu, tak rychle se chodí s džbánem pro vodu, až se ucho utrhne.
Závěrem ještě poznámku o soustavách rovnic. Uvažujme opět:
y'' - 4y = 0
Tuto rovnici druhého řádu bychom mohli převést na dvě rovnice prvního řádu takto:
Zavedeme si novou neznámou funkci z, která bude derivací té původní:
z(x) = y'(x)
Když obě strany zderivujeme, dostaneme vyjádření pro y'' pomocí z'
z'(x) = y''(x)
a tu druhou derivaci nahradíme z naší rovnice (y'' = 4y):
z'(x) = 4y
Takže suma sumárum dostaneme místo jedné rovnice druhého řádu dvě rovnice prvního řádu (substituční formulku a původní rovnici, kde jsme druhou derivaci nahradili první derivací nové funkce):
y'(x) = z(x)
z'(x) = 4y(x)
I jejich řešení se dá provést pomocí exponenciál, ale už je komplikovanější, protože abychom pravou stranu nějak ukočírovali, musíme nasadit do hry matice a jejich vlastní čísla, a to přenecháme koňovi. Inu, darovanému koni na vlastní čísla nekoukej.
Nelineární systémy
(v této sekci budu používat některé pojmy z
minula)
Jak už to tak v životě bývá, diferenciální rovnice, které se dají vyřešit, nejsou moc praktické, zatímco rovnice, které praktické jsou, se zhusta vyřešit nedají. Podívejme se tedy okrajově na alternativní způsob jejich řešení pomocí přibližných numerických metod.
Vezmeme si trochu zjednodušený fyzikální problém hmotného bodu pohybujícího se v silovém poli. Pro jednoduchost budeme předpokládat, že sílu F v bodě r reprezentuje 2D vektorové pole F(r) znázorněné na obrázku vlevo (většinu problémů je ovšem nutno popsat ve vícerozměrném konfiguračním) či fázovém prostoru).
tím je dointegrováno a teď už je z toho jen funkční rovnice ne nepodobná té z úvodu, kterou prostě algebraicky dotvarujeme kladívky, tj. aplikujeme exponenciálu na obě strany
y = exp(-x2) * K
(kde K je exp(C))
a řešením jsou kladné násobky funkce exp(-x2).
Diferenciální rovnice tedy mají nekonečně mnoho řešení. Abychom z nich dostali pouze jedno, musíme ještě na hledanou funkci y(x) uvalit dodatečnou podmínku, která většinou (ale ne vždy) specifikuje hodnotu funkce v nule (proto se jí říká počáteční podmínka): tedy např. y(0) = 2 (na obrázku vpravo vyznačena zeleně).
Pojďme ho najít. Když si do předchozího obecného řešení dosadíme x = 0, dostaneme
y(0) = exp(0) * K
a tedy
2 = 1 * K
a funkce splňující naši diferenciální rovnici se zelenou počáteční podmínkou bude odpovídat hodnotě K = 2.
y(x) = 2 * exp(-x2)
Pochopitelně ne každá diferenciální rovnice se dá separovat, proto se občas musí nasadit přibližné numerické metody – ale o tom až za chvíli. Inu, čiň čertu dobře, numerickými metodami se ti odmění.
Před časem jsme viděli, že existují i derivace vyšších řádů a i ty se mohou v diferenciálních rovnicích vyskytovat. Např. Newtonův zákon obsahuje zrychlení, což je druhá derivace polohy podle času (první derivace je rychlost), takže velmi často najdeme rovnice obsahující druhé derivace v klasické mechanice.
Jako příklad se podívejme na tzv. lineární rovnici druhého řádu (nalevo je lineární kombinace funkce a jejích derivací).
y'' - 4y = 0 neboli y'' = 4y
(hledáme zde funkci, jejíž druhá derivace je čtyřnásobek funkční
hodnoty)
Tento typ rovnic se opírá o známou skutečnost, že exponenciála je vůči derivaci imunní, a pokud do ní ještě vložíme konstantu, je skoro imunní:
(exp(kx))' = k exp(kx)
což z pohledu integrování znamená
∫ exp(kx) dx = exp(kx) / k
A tato vlastnost exponenciály nám umožní převést integraci na algebraický problém.
Zkusme tedy hledat řešení rovnice y'' - 4y = 0 ve tvaru
y(x) = exp(kx)
s tím, že zatím neznámou konstantu k zvolíme tak, aby rovnice „vyšla“ (což je pro tento typ rovnic možné díky zmíněné „imunitě“).
Když si spočítáme druhou derivaci takto zvolené funkce, obdržíme:
y'' = k2 exp(kx)
a dosazením funkce i druhé derivace (v tomto tvaru) do rovnice nám dá:
k2 exp(kx) - 4 exp(kx) = 0
Exponenciála je vždy kladná, takže ji můžeme zkrátit, aniž by nám hrozilo dělení nulou.
k2 - 4 = 0
a to je snadná kvadratická rovnice s řešením k = 2 a k = -2
Dvě konkrétní řešení naší rovnice jsou tedy exp(2x) a exp(-2x) a obecné řešení pak dostaneme jejich lineární kombinací.
y(x) = A exp(2x) + B exp(-2x)
Takových funkcí je mnoho a abychom z nich dostali jednoznačné řešení, potřebovali bychom dvě počáteční podmínky, protože máme v obecném řešení dvě neznámé konstanty. Například bychom mohli zadat funkci ve dvou různých bodech:
y(0) = 1 a y(1) = 2
anebo zadat funkci PLUS derivaci v jednom bodě
y(0) = 1 a y'(0) = 2.
S druhou možností se opět velmi často setkáváme ve fyzice, protože abychom mohli studovat pohyb bodu v nějakém silovém poli, musíme znát nejen počáteční polohu, ale také počáteční rychlost. Inu, tak rychle se chodí s džbánem pro vodu, až se ucho utrhne.
Závěrem ještě poznámku o soustavách rovnic. Uvažujme opět:
y'' - 4y = 0
Tuto rovnici druhého řádu bychom mohli převést na dvě rovnice prvního řádu takto:
Zavedeme si novou neznámou funkci z, která bude derivací té původní:
z(x) = y'(x)
Když obě strany zderivujeme, dostaneme vyjádření pro y'' pomocí z'
z'(x) = y''(x)
a tu druhou derivaci nahradíme z naší rovnice (y'' = 4y):
z'(x) = 4y
Takže suma sumárum dostaneme místo jedné rovnice druhého řádu dvě rovnice prvního řádu (substituční formulku a původní rovnici, kde jsme druhou derivaci nahradili první derivací nové funkce):
y'(x) = z(x)
z'(x) = 4y(x)
I jejich řešení se dá provést pomocí exponenciál, ale už je komplikovanější, protože abychom pravou stranu nějak ukočírovali, musíme nasadit do hry matice a jejich vlastní čísla, a to přenecháme koňovi. Inu, darovanému koni na vlastní čísla nekoukej.
Nelineární systémy
(v této sekci budu používat některé pojmy z
minula)
Jak už to tak v životě bývá, diferenciální rovnice, které se dají vyřešit, nejsou moc praktické, zatímco rovnice, které praktické jsou, se zhusta vyřešit nedají. Podívejme se tedy okrajově na alternativní způsob jejich řešení pomocí přibližných numerických metod.
Vezmeme si trochu zjednodušený fyzikální problém hmotného bodu pohybujícího se v silovém poli. Pro jednoduchost budeme předpokládat, že sílu F v bodě r reprezentuje 2D vektorové pole F(r) znázorněné na obrázku vlevo (většinu problémů je ovšem nutno popsat ve vícerozměrném konfiguračním) či fázovém prostoru).
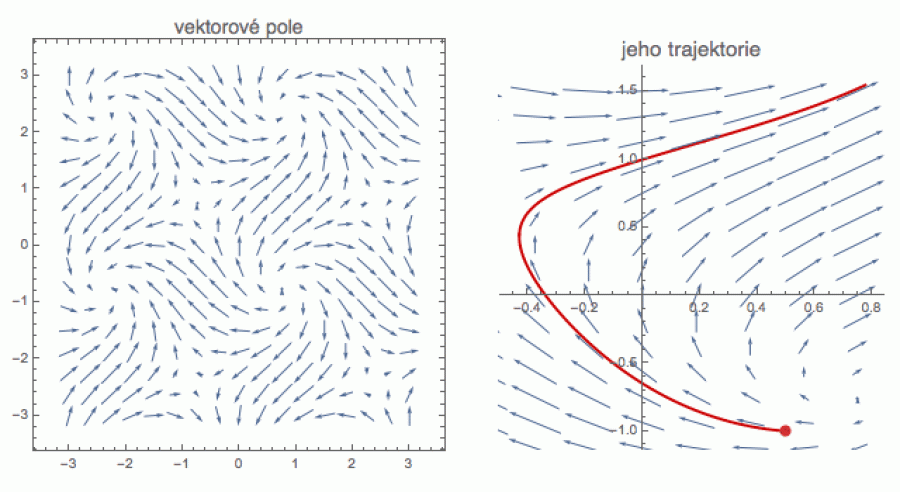
Mechanika problému je vcelku jednoduchá. Každý bod vložený do tohoto pole se pohybuje ve směru síly, tedy podél naznačených šipek. Viz červený bod v pravé části obrázku, který ukazuje detail předchozího pole. Pokud bychom si červený bod vybrali jinde, jeho trajektorie by byla trochu jiná (zobrazení, které každou počáteční podmínku posune podél příslušné trajektorie o nějaký pevný čas T, se říká tok vektorového pole – ale to jen tak pro zasmání).
A teď přesněji: když si označíme červenou křivku pohybujícího se bodu r(t) = (x(t),y(t)), kde t je čas a r je 2D polohový vektor, pak požadujeme, aby tečný vektor k této křivce splýval s vektorem působící síly v tom bodě. Minule jsme si řekli, že tečný vektor ke křivce je derivací její parametrizace, takže pro pohybové rovnice dostaneme:
(+) r'(t) = F(r(t)) nebo zjednodušeně r' = F(r)
To je v našem případě systém dvou diferenciálních rovnic.
x'(t) = f(x(t),y(t))
y'(t) = g(x(t),y(t))
(kde f, g jsou známé složky vektoru F a x,y neznámé
složky vektoru r)
Hledáme tedy dvě funkce x, y proměnné t, splňující tyto dvě rovnice. Protože f a g jsou obecně nelineární funkce, nemůžeme použít metody lineární algebry (jak jsem je naznačil v předchozí sekci), ale musíme na problém nasadit numerické algoritmy. To znamená nasekat čas na diskrétní kousíčky a pokusit se polohový vektor r(t) vyčíslit numericky (pro každý diskrétní čas t) z předchozího vektoru.
Zkusme se nejprve zamyslet, jak bychom to sami udělali: někdo na nás namíří bambitku a řekne nám, že v čase t je systém v bodě r, a naším úkolem je zjistit, kde bude systém v čase t + Δt (Δt je malý časový nárůst, jehož velikost odpovídá tomu, jak nadrobno jsme si nasekali čas).
Selským rozumem bychom řekli, že bod se kousek posune ve směru síly F(r). Takže pokud na nás pořád míří ta bambitka, tak bychom k bodu r přičetli malý násobek F(r). Jen musíme použít definici derivace, abychom ho dokázali správně odhadnout.
Derivace je limita následujícího výrazu (pro Δt --> 0)
r'(t) = lim (r(t+Δt) - r(t)) / Δt
(je to tedy rozdíl poloh vydělený časovým přírůstkem)
A protože limita je více méně vyčíslením daného výrazu pro zmenšující se hodnoty Δt, využijeme toho, že naše Δt je dostatečně malé, a limitu ve formulce (+) drze nahradíme podílem pro tuto malou hodnotu.
r'(t) ~ (r(t + Δt) - r(t)) / Δt = F(r(t))
a protože pole F je zadané, můžeme po úpravě odhadnout novou polohu:
r(t + Δt) = r(t)) + Δt * F(r(t))
Nová poloha je tedy stará poloha plus malý násobek vektoru síly, což je prakticky naše selskorozumové řešení. Technicky se mu říká Eulerova metoda.
Ta ale sama o sobě moc přesná není, protože tiše předpokládáme, že síla se během pohybu v časovém intervalu (t, t + Δt) nemění, což pochopitelně není pravda: jakmile vyrazíme z bodu r podél vektoru F, směr síly se začne okamžitě měnit. V praxi se proto používají přesnější metody (např. Runge-Kutta, Adams-Moulton atd.), které se pokoušejí do výsledné nové polohy tuto změnu zahrnout.
Kdyby vědci na mysu Canaveral používali pro výpočet trajektorií Eulerovu metodu, tak by raketa po šesti hodinách letu na Měsíc přistála pravděpodobně v Horních Počernicích. Inu, i mistr analytik se někdy utne.
Zkoumání trajektorií různých systémů (většinou pomocí diferenciálních rovnic) spadá do oblasti matematiky, které se říká dynamické systémy (viz též toto a toto Matykání).
Jednou z nejdůležitějších vlastností dynamických systémů je poloha pevných bodů (ekvilibrií), což jsou body, kde je vektorové pole nulové: F(r) = 0 (toto obvykle vede na nelineární soustavu algebraických rovnic, které se řeší Newtonovou metodou). Tyto body mají tu speciální vlastnost, že pokud do nich vložíme ten hmotný bod, tak bude sedět na fleku, protože na něj nebude působit žádná síla.
Nejdůležitějším aspektem pevných bodů je jejich stabilita. Tedy co se s nimi stane, pokud do bodu maličko šťouchneme. Pro stabilní ekvilibria se bod po šťouchnutí vrátí do původní polohy. Pro nestabilní se odkutálí pryč.
Klasická představa kuličky v údolí, respektive na kopci je sice velmi vizuální, ale o chování pevného bodu, který jsme právě v potu tváře vyždímali z vektorového pole, nám toho mnoho neřekne.
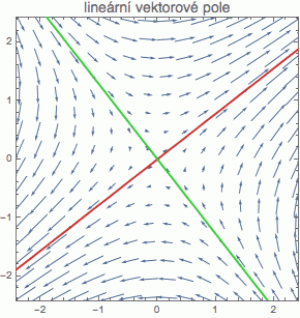
Pro lineární systémy, kdy se chování pole dá popsat maticí A (pole pak má formu skalárního součinu F(r) = A.r) existuje jediné ekvilibrium r = 0 a jeho chování je plně popsáno chováním vlastních čísel matice A. Pokud jsou kladná, tak kulička podél příslušných vlastních vektorů odběhne, pokud jsou záporná, tak se vrátí.
To je vidět z toho, že pro vlastní vektor r s číslem λ je působící síla rovna
F(r) = A.r = λr
To znamená, že pro λ > 0 působí síla ve směru vychýlení r (odvane kuličku pryč), zatímco pro λ < 0 působí proti němu (když kuličku vychýlíme, síla ji bude vracet zpět). Na obrázku vpravo je vektorové pole určené maticí A = ((1,2), (2,0)) s tím, že zelený směr odpovídá zápornému λ (pole nám bude vracet bod nazpátek), zatímco červený směr odpovídá kladnému λ (pole nám bod odkutálí pryč).
Většina realistických polí samozřejmě lineární není, ale nabízí se možnost najít lokální lineární aproximaci pole F v okolí ekvilibria r a tu pak zkoumat pomocí vlastních čísel.
Minule jsme viděli, že lineární aproximace je definovaná derivací, která má v případě vektorových polí formu Jacobiho matice vyčíslené v bodě r. Vlastní čísla a vlastní vektory této matice pak ukazují – stejně jako v lineárním případě – směry, ve kterých má diferenciální rovnice snadno uchopitelné chování (lokální). Samozřejmě, jakmile z ekvilibria poodběhneme, Jacobiho matice své aproximační kouzlo ztratí. Inu, kdo nic neaproximuje, nic nezkazí.
Lorentzův systém
V roce 1963 se americký meteorolog Edward Lorenz snažil pochopit zákonitosti proudění v atmosféře. A protože se v té době začaly rozmáhat numerické simulace dynamických systémů pomocí počítačů, sestrojil si poměrně jednoduchý model, který sice nereprezentuje žádný konkrétní meteorologický jev (na to je příliš zjednodušený), ale sám o sobě vykazuje zajímavé chaotické chování, které posílilo názor, že počasí je v zásadě nelineární obtížně předvídatelný systém.
Za základ své práce si vzal tzv. Boussinesqovu aproximaci) rovnic pro proudění kapalin v tenké vrstvě. To je sice parciální diferenciální rovnice (tj. kromě časových derivací obsahuje také prostorové derivace, které naznačují, jak se fyzikální veličiny – teplota, tlak, hustota atd. – mění s polohou), ale díky rozvinutí členů do určitého ekvivalentu Fourierovy řady se mu podařilo prostorové derivace nahradit algebraickými vztahy a po restrikci na pouhé tři členy zmíněné řady obdržel tři obyčejné diferenciální rovnice v poměrně jednoduchém tvaru (zde je odvození).
x' = s(y-x)
y' = x(r-z) - y
z' = x y – bz
kde b, r, s jsou fyzikální parametry a x, y, z jsou hledané funkce času (jejich časové derivace jsou na levé straně). Všimněte, že je to stejný typ rovnic jako v předchozí sekci, jen máme o jednu dimenzi navíc.
Tyto rovnice (říká se jim Lorenzův systém) jsou nelineární – na pravé straně nejsou jen lineární kombinace hledaných funkcí, ale i násobky funkcí mezi sebou – a to komplikuje jejich řešení natolik, že je nutno je simulovat (řešit) numericky, metodami naznačenými v předchozí sekci.
Stejně jako předešlé diferenciální rovnice i Lorenzův systém potřebuje počáteční podmínky, tedy hodnoty x(0), y(0), z(0) - a z nich pak pomocí numerických řešení odvodí konkrétní trajektorie systému. Pravá strana zde definuje 3D vektorové pole F(x, y, z) a počáteční bod do tohoto pole vložený se pak pohybuje ve směru šipek.
Zabalme si pro pohodlí tři proměnné do polohového vektoru
r = (x, y, z)
Na dalším obrázku je naznačena jedna trajektorie systému pro určitou konkrétní podmínku r(0), která odpovídá začátku tmavší části trajektorie (v levé části je zčásti překryta). Ta „niť“ jedné konkrétní trajektorie tedy „sleduje“ směr vektorového pole stejně jako ta červená trajektorie z předchozí sekce. Protože je systém 3D, promítneme si ji do tří souřadných rovin.
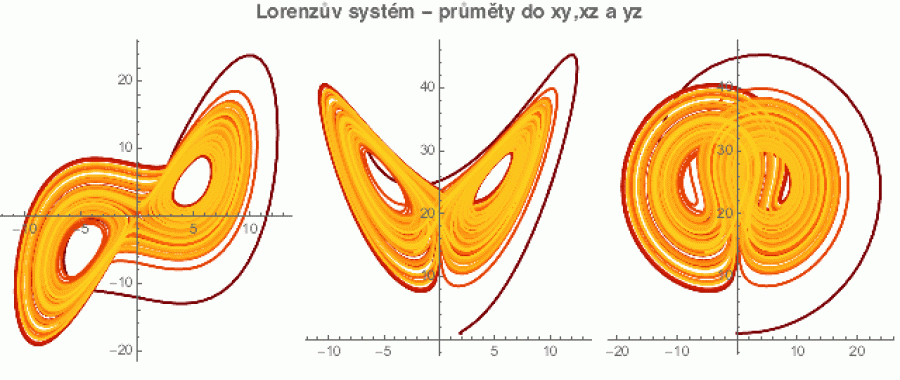
Obecné chování tohoto systému je takové, že trajektorie po startu z r(0) chvíli bloudí po prostoru (to je ta tmavší část), ale pak se začne poměrně stabilně „namotávat“ na dvojici „vírů“, které se říká Lorenzův atraktor. A v tomto dvojvíru pak zůstane „uzamčena“.
(zde je hezká simulace a tady si s tím můžete hrát sami)
Simulace řešení ukázala, že získané trajektorie vykazují citlivou závislost na počáteční podmínce (což je jeden z charakteristických znaků chaotických systémů).
Abychom si o ní udělali představu, následující dvojobrázek ukazuje vždy pár trajektorií odvozených z páru počátečních podmínek r(0) a R(0). Trajektorie odpovídající r je vyznačena modře, trajektorie odpovídající R červeně. V levé části obrázku jsou obě počáteční podmínky poměrně vzdáleny, a obě trajektorie se proto výrazně liší.
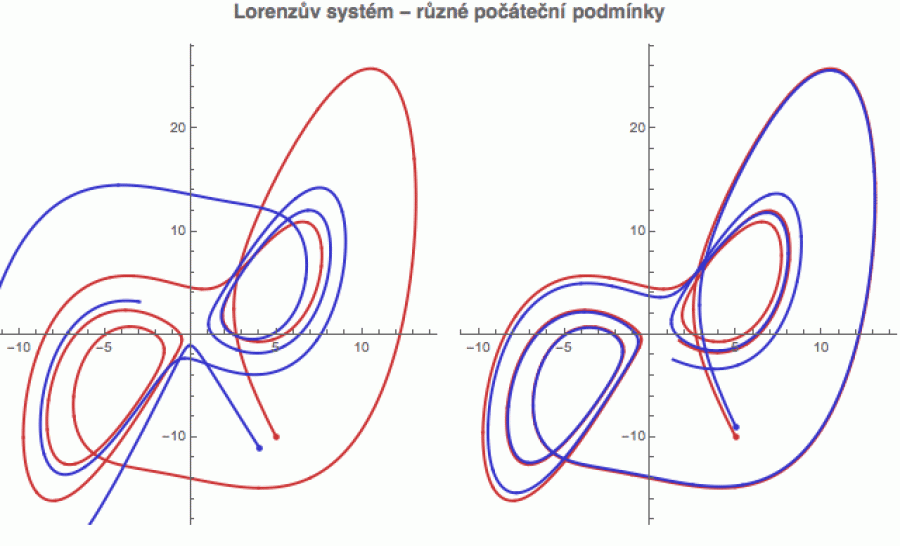
Napravo jsou si obě počáteční podmínky blízko, takže zpočátku se trajektorie prakticky neliší, ale přesto se nakonec od sebe odchýlí (pokud rovnice simulujeme pro dostatečně dlouhý čas). A to je obsahem citlivé závislosti na počáteční podmínce: když do té první počáteční podmínky R trochu „drkneme“ (a dostaneme z ní r), tak se výsledná trajektorie od té původní nakonec zcela odchýlí. To „drknutí“ má tedy za následek kvalitativní změnu chování systému. Systém na něj reaguje „citlivě“.
Čím blíž jsou si r a R, tím delší čas na ten rozchod budeme potřebovat. To má z pohledu meteorologie (a dynamických systémů obecně) následující interpretaci:
U realistických fyzikálních systémů neznáme nikdy přesně všechny proměnné a parametry, protože jejich měření jsou zatížena chybami. Předpokládejme, že skutečná (červená) hodnota počáteční podmínky bude R. Tu pochopitelně neznáme. My známe jen naměřenou (modrou) hodnotu r. Červená trajektorie odpovídající R by odpovídala skutečnému chování fyzikálního systému (řekněme počasí), zatímco hodnota r vygeneruje trajektorii, která bude odpovídat chování našeho modelu.
Pokud se trajektorie „po dobu simulace“ od sebe příliš neliší, nic se neděje. Skutečné i modelem předpovězené chování jdou ruku v ruce. Pokud ale systém vykazuje citlivou závislost, pak se skutečná trajektorie odvozená z R bude dříve či později zásadně odlišovat od modelové trajektorie odvozené z naměřené podmínky r.
Básnicky se tomuto fenoménu říká motýlí efekt, protože přechozí diskuze se dá interpretovat takto: Představme si, že někde v Uruguayi zatřepetá motýlek křídly. To trochu změní počáteční podmínku atmosférického systému, takže po určité době se nový systém (odpovídající počáteční podmínce po „zatřepetání“) začne chovat úplně jinak. A po dostatečně dlouhé době si systém může projít úplně jinými stavy. Náš nevinný motýlek tím pádem může způsobit např. tornádo v Kansasu.
Proto je krátkodobá předpověď relativně spolehlivá, protože počáteční podmínky jsou si při dnešní citlivosti přístrojů poměrně blízko, takže k rozchodu potřebují delší čas. Pro malé časy se obě trajektorie (skutečná i naměřená) chovají zhruba podobně – jak je naznačeno v pravé části předchozího obrázku. Pro delší časy už se ale i velmi podobné počáteční podmínky rozejdou. Proto je prakticky nemožné říci, jaké bude počasí za měsíc. Ono i za týden je to tak tak.
Samozřejmě moderní meteorologické modely už ty parciální diferenciální rovnice neaproximují nějakými třemi členy (jako to udělal Lorenz), ale přímo je simulují pomocí speciálních numerických metod – ne nepodobných té Eulerově, ale s více derivacemi. Ale to už by byla jiná pohádka. A abych jednu pohádku závěrem parafrázoval: K parciálkám se nečuchá!
Článek je redakčně upravenou verzí blogového příspěvku na serveru iDNES.cz. Publikováno s laskavým svolením autora. Další díly a původní texty jsou dostupné na blogu Jana Řeháčka.