Jednoho rána přistoupila kvadratická rovnice k nablýskanému zrcadlu: „Zrcadlo, zrcadlo, ptám se tě, která rovnice je nejkrásnější na světě?“ A byla překvapena, že v chaloupce u sedmi komplexních trpaslíků jí roste kalá konkurence.

V roce 1988 uspořádal popularizační časopis Mathematical Intelligencer mezi svými čtenáři anketu o nejkrásnější rovnici světa. 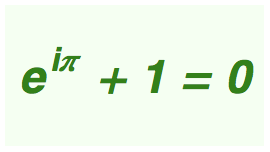Přesvědčivě v ní zvítězila tzv. Eulerova identita, úhledná rovnice svazující pět základních matematických konstant (0, 1, i, e, π) prostřednictvím překvapivě jednoduchého vztahu (viz obrázek vpravo). Její pozici světové jedničky mezi rovnicemi, tedy jakési pomyslné Miss Equation, před pár lety potvrdili i redaktoři BBC, kterým se na Eulerově mistrovském kousku líbilo hlavně sloučení zdánlivě nesouvisejících čísel v jeden hutný a koncizní celek.

Leonardo da Vinci kdysi řekl, že „jednoduchost je nejvyšší formou sofistikovanosti“. Elegance, s kterou tato rovnice spojuje obě mystické konstanty e a π, jí přisuzuje kultovní status mezi příznivci královny věd (postavení Eulerovy identity není zcela nepodobné roli, kterou hraje Einsteinova rovnice E = mc² ve fyzice, i když její popularity zdaleka nedosahuje).

V dnešním Matykání se podíváme, odkud se tato rovnice vzala a jaké jsou její důsledky.

(z typografických důvodů ji budu zapisovat jako: exp(iπ)+1=0)

+++++++++

Komplexní funkce

Komplexní funkci si - stejně jako její reálný protějšek - můžeme představovat jako skříňku s trpaslíkem. Vhodíte do ní komplexní číslo, trpaslík s ním podle přesně definovaného algoritmu provede určitou operaci - aritmetickou, geometrickou nebo jakoukoliv jinou - a nakonec vám na výstupu vyhodí další komplexní číslo. Ve volné přírodě poznáte komplexního trpaslíka snadno - na rozdíl od svého reálného kolegy má na hrudi vytetované kapitánské céčko (C = complex).

Vstupní proměnná se obvykle značí z a výstupní w. Komplexní funkce tedy nemají obecný tvar y = f(x), ale w = f(z).

Většina užitečných pojmů (definiční obor, obor hodnot, spojitost, linearita, inverzní funkce, derivace) se dá převzít přímo z reálné analýzy a s jejich definicí nejsou těžkosti.

Úplně všechno se ale do komplexního jazyka přeložit nedá. Třeba monotonie by se definovala jen ztěžka, protože na komplexních číslech - na rozdíl od těch reálných - neexistuje přirozené uspořádání, které by nám vždy umožnilo rozhodnout, které ze dvou čísel je větší (je např. íčko větší než jednička?). Proto pojmy jako funkce rostoucí nebo klesající v komplexním oboru moc smyslu nedávají.

Další velký problém nastane v okamžiku, kdy se danou komplexní funkci budeme snažit nakreslit.

V reálné analýze je to jednoduché. Vstup i výstup jsou jednorozměrná „čísla“, takže znázornění funkce se provede v dvourozměrné rovině x-y. Z obrázku pak lehce odečteme, jak jsou jednotlivé vstupy (x) přeměňovány na výstupy (y).

U komplexních funkcí je vstup i výstup de facto dvourozměrný (komplexní číslo je bod v rovině), a tak bychom na ekvivalentní „obrázek“ potřebovali čtyřrozměrný graf (dvě dimenze na osu w a další dvě na osu z). Něco tak divokého by však naše oči nezvládly.

Prozatím si je tedy budeme představovat tak, že si vytvoříme dvě kopie komplexní roviny - jednu pro vstup (in) a druhou pro výstup (out). Ve vstupní rovině si vybereme nějaký bod (komplexní číslo), hodíme ho trpaslíkovi do krabičky a vypadne nám výstupní komplexní hodnota (také bod), kterou vyneseme ve výstupní rovině.

Na dalším obrázku je to schematicky vyznačeno pro funkci f(z) = z² + 1. Bod z = i (modrý míček) se zobrazí na výstupní hodnotu w = 0. Sami si můžete ověřit, co se stane s míčkem v bodě z = 1 (červený). Další dva míčky sedící v obecných desetinných číslech jsem zobrazil počítačem. Toto je velmi hrubý nástin chování funkce f, ale prozatím nám to bude stačit.

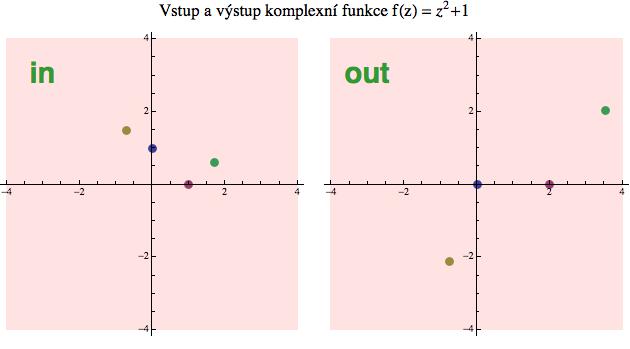
Tento obrázek nám také umožní pochopit princip inverzní funkce. Stejně jako v reálném případě, inverzní funkce převádí výstupy zpět na vstupy. Pokud daná funkce zobrazuje z na w, tak funkce inverzní musí zobrazit w zpátky na z. Původní funkce tedy bere vstupní „míčky“ a přiřazuje jim „míčky“ výstupní, zatímco funkce inverzní dělá pravý opak - z míčků výstupních dělá míčky vstupní. Naše funkce z² + 1 přiřadila bodu z = i (modrý míček) výstupní hodnotu w = 0. To znamená, že inverzní funkce, což je v podstatě sqrt(w-1), musí zobrazit 0 na i.

Spojitost funkce - stejně jako v reálném případě - znamená, že malá změna vstupní proměnné zaručuje malou změnu proměnné výstupní. A tu velikost, respektive malost změny dokážeme celkem lehce kvantifikovat pomocí absolutní hodnoty rozdílu. Žádný velký problém nepředstavuje ani derivace a s ní spojený pojem „hladkosti“. Hladké komplexní funkce - zvané holomorfní nebo též analytické - patří k nejužitečnějším objektům komplexní analýzy (ty si ale vyžádají zvláštní Matykání).

Dalším důležitým, a z reálné analýzy lehce přenositelným pojmem je kořen funkce - tedy taková vstupní hodnota z, která nám na výstupu dá nulu. Snaha o jeho nalezení vede k řešení rovnice: f(z) = 0 (tady mám samozřejmě na mysli komplexní nulu: 0 + 0i). V jednoduchých případech se kořeny dají najít algebraicky, tak jako to dělávaly naše babičky, v obtížnějších se hledají pomocí numerických metod.

+++++++++

Nejznámějšími funkcemi jsou polynomy. Tedy funkce odvozené z aritmetických operací, kde se dá výstupní hodnota spočítat přímo z vlastností komplexních čísel. Například funkce w = z² funguje přesně tak, jak si asi představujete. Hodíte do ní i, vypadne vám f(i) = -1. Hodíte do ní 5, vypadne vám f(5) = 25. Vhodíte 2 + i, vypadne vám f(2 + i) = 3 + 4i. Pro každé číslo z vám trpaslík na výstupu podá jeho čtverec z² - nic víc v tom není.

Pro polynomy vyšších stupňů se vyplatí znát mocniny i. Není to nic těžkého, prostě každou předchozí vynásobíme dalším íčkem a zjednodušíme. Takže například i³ = i² * i = (-1)*i = -i. A obdobně pro ty další. Nakonec dostaneme tuto posloupnost (a začnu nultou mocninou):

1, i, -1, -i, 1, i, -1, -i, 1, i, -1, -i, 1, i,...

(čtyři první mocniny se vlastně stále točí dokola)

Můžete si to procvičit na funkci w = g(z) = z³ - 2z + 1.

Její hodnota v bodě i je snadná: g(i) = i³ - 2i + 1 = -i - 2i + 1 = 1 - 3i

A kdo si chce započítat, může si zkusit ukázat, že g(2 - 3i) = -49 - 3i.

Experti si mohou troufnout i na desetinná čísla: g(1.2 + 0.7i) = -1.436 + 1.281i

Ovšem nejen polynomy živ je matematik. Nejdůležitější funkcí - a v komplexním případě to platí dvojnásob - je stále exponenciála. Ta všudypřítomná tetička známá v reálném případě jako „é na x“ alias exp(x).

+++++++++

Komplexní exponenciála

Důležitou vlastností reálné exponenciály je, že převádí součet na součin, tedy že pro každou dvojici reálných čísel a,b platí exp(a + b) = exp(a) * exp(b). Tento vztah nám umožní nahlédnout i do struktury komplexní exponenciály (která se nedá přímo dovodit z algebraických vlastností komplexních čísel, protože jsme si zatím neřekli, jak umocnit reálné číslo - zde e - na komplexní exponent).

Nuže vezměme si nějaké komplexní číslo z = x + iy a šup s ním do trpaslíkovy krabičky:

exp(x + iy) = exp(x) * exp(iy)

První část výrazu napravo je jasná - to je obyčejná reálná exponenciála. Stačí tedy, když pochopíme, co exponenciála dělá s čísly imaginárními (násobky íčka) a máme vystaráno.

To ale není nikterak jednoduchý problém a budeme se muset odkázat na vyjádření transcendentních funkcí pomocí nekonečných polynomů. Tyto polynomy (přesněji řady) nám vlastně ukazují, jak se dá daná funkce přeformulovat pomocí (nekonečně mnoha) algebraických operací (a ty už s íčkem umíme docela dobře).

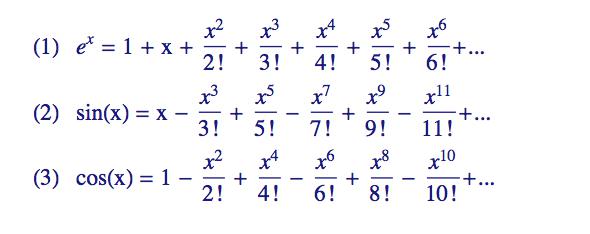
(Stále jsem vám ještě neprozradil, jak si ty nekonečné polynomy spočítat - k tomu se dostaneme, až se vrátíme k diferenciálnímu počtu. Zatím si je představujte jako aproximace s tím, že čím více členů na pravé straně si vezmete, tím lepší aproximaci získáte. A pokud si je vezmete všechny, podaří se vám tu funkci zrekonstruovat přesně.)

A teď s těmi nekonečnými polynomy začneme čarovat.

Nejprve si do (1) dosadíme ix, abychom viděli, co to mysteriózní íčko s naší exponenciálou udělá. Pak si v (5) všechny mocniny íčka zjednodušíme (viz závěr předchozí sekce) a v (6) následně odseparujeme výrazy, které íčko obsahují, od těch, které ho neobsahují. V (7) íčko vytkneme, zbylé členy zjednodušíme a pak si uvědomíme, že v závorkách máme de facto nekonečné polynomy pro sin a cos - viz (2) a (3) - a tím dostaneme závěrečný vztah, slavnou Eulerovu formulku (8). Rovnice (9) už pak jen všechno smontuje dohromady v komplexní exponenciálu (a tam už imaginární část značím y).

Teď už tu nejkrásnější rovnici světa máme takřka na dosah. Stačí si do (8) dosadit x = π (což je úhel v radiánech odpovídající 180°). Pravou stranu si buď vyčíslíme pomocí sinu a kosinu, anebo si uvědomíme, že na jednotkové kružnici odpovídá 180° (měřeno od kladné osy x) právě bodu -1. Takže dostaneme exp(iπ)= -1 a jsme doma.

Mimochodem, i známá Moivreova věta je důsledkem rovnice (8):

(cos(x) + i sin(x))^n = (exp(ix))^n = exp(inx) = cos(nx) + i sin(nx)

(zde je záhodno učinit přestávku na svačinu)

+++++++++

Dalším důsledkem této malé odysey do světa řad je pozoruhodný fakt, že exp(ia) je komplexní číslo na jednotkové kružnici odpovídající úhlu a (v radiánech!). Jak se reálné číslo a zvětšuje, bod exp(ia) obíhá po kružnici proti směru hodinových ručiček pořád dokola. Z rovnice (9) dále vyplývá, že komplexní exponenciála je periodická funkce s periodou 2πi, tj. kdykoliv si vezmeme dva body lišící se o tuto hodnotu, exponenciála je zobrazí na stejný bod ve výstupní rovině.

Komplexní exponenciála nám také umožňuje vyjádřit polární souřadnice komplexního čísla ve velmi kompaktní formě (viz níže bleděmodrý bod s poloměrem r a úhlem b - měřeným od kladné osy x).

z = r*exp(ib)

Samozřejmě bychom ty souřadnice mohli vyjádřit klasicky:

x = r cos(b)
y = r sin(b)

ale při algebraické manipulaci bychom pak museli ty siny a kosiny neustále přehazovat vidlemi a taková věc se brzy omrzí.

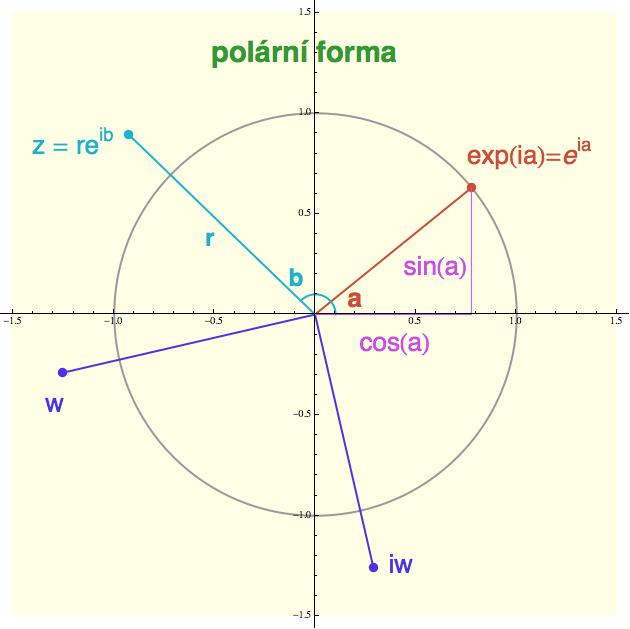
Polární forma komplexního čísla nám poskytuje nový pohled na mechaniku komplexního násobení. Zatímco v kartézských souřadnicích vypadá celkem neprůstřelně, v polárních má velmi jednoduchou formu:

r*exp(ia) * s*exp(ib) = rs * exp(i(a+b))

Při součinu dvou komplexních čísel zapsaných v polárních souřadnicích prostě vynásobíte poloměry a sečtete úhly.

Jako jednoduchý příklad si ukážeme, co se stane, když dané komplexní číslo w = r*exp(ic) vynásobíme íčkem (viz modrá část obrázku nahoře). Íčko se polárně vyjádří jako exp(iπ/2), kde π/2 je pravý úhel vyjádřený v radiánech (poloměr tady nepotřebujeme, protože absolutní velikost íčka je 1). Vynásobení čísla w íčkem tedy v polárních souřadnicích vypadá takto:

r*exp(ic) * exp(iπ/2) = r * exp(i(c+π/2))

a to znamená, že po vynásobení se číslo w prostě pootočí o pravý úhel (jeho polární úhel c se zvětší o π/2). Kdo ovládá vektory, může si tu kolmost odvodit i z kartézského vyjádření. Pokud je w = x + iy, bude iw = -y + ix a vektor {-y,x} je samozřejmě kolmý na ten původní {x,y} (jejich skalární součin je nula).

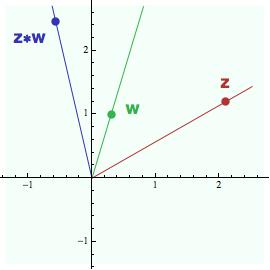
Ten součin v polárních souřadnicích také znamená, že si jeho fungování můžete představit pomocí následující vizuální hračky (viz obrázek vpravo).

Vezmeme si dvě komplexní čísla z a w, a zakreslíme si jejich součin z * w (modrý míček). Když teď budeme s těmi čísly z a w pohybovat po naznačených polopřímkách, tedy tak aby jejich polární úhel byl stále stejný, pak jejich komplexní součin (modrý míček) bude také muset zůstat na modré polopřímce (nezměnili jsme polární úhel z ani w, takže se nesmí změnit ani polární úhel z*w - který je jejich součtem). A můžete si rozmyslet, jaký vliv má na pohyb modrého míčku současné posunování tím zeleným a červeným.

Z tohoto pohledu vyplývá, že komplexní násobení není zase tak úplně neintuitivní, jak by se mohlo zdát z jeho kartézského vyjádření, a určité přirozené zákonitosti splňuje.

+++++++++

Podívejme se teď na rovnici komplexní exponenciály w = exp(z) ještě jednou:

w = exp(x+iy) = exp(x) * exp(iy) = r * exp(iy)

Výraz exp(x) je vždy kladné číslo a můžeme si ho tedy představit jako polární poloměr r. Exponenciála tedy v jistém smyslu převádí kartézské souřadnice na polární.

A tady si dovolím malou filosofickou odbočku.

Komplexní číslo - jakožto bod v rovině - má v podstatě dvě formy vyjádření. Algebraická z = x + iy odpovídá kartézským souřadnicím, zatímco exponenciální z = r*exp(ia) odpovídá souřadnicím polárním (poloměr r a úhel a). Tyto formy mají velmi rozdílné vlastnosti, co se týče základních aritmetických operací - sčítání a odčítání.

Kartézské souřadnice jsou velmi snadné - a přímo bych řekl intuitivní - pokud se jedná o součet. Prostě sečtete příslušné souřadnice - reálné a imaginární části - separátně.

(a + ib) + (c + id) = (a + c) + i (b + d)

Násobení - jak jsem poznamenal výše - už je trochu neintuitivní:

(a + ib) * (c + id) = (ac - bd) + i (ad + bc)

U polárních souřadnic je tomu naopak. Násobit v nich je přímo pohoda:

r*exp(ia) * s*exp(ib) = rs * exp(i(a+b))

Se součtem je to horší. Možná si říkáte, že součet dvou čísel vyjádřených v polárních souřadnicích by se také měl dát zmáknout (tedy vyjádřit nějakou změtí daných polárních poloměrů r, s a úhlů a, b). No tak si to schválně zkuste:

r*exp(ia) + s*exp(ib) = grrrrrrr... vrrrrrrr... arrrrgh...

Ne, není to žádná legrace. Samozřejmě spočítat se to dá - a nebudete na to potřebovat víc než středoškolskou matematiku - ale není to podívaná pro slabé žaludky (kdo si na to troufá, může se mrknout sem).

A co tím chtěl básník říci?

Básník tím chtěl říci, že v matematice - zejména v teorii čísel - je spousta problémů, které souvisí s tím, že sčítání a násobení jsou v jistém smyslu nekompatibilní operace. Například spočítat faktorizaci součtu dvou čísel, jejichž rozklad na prvočinitele známe, je zatraceně těžký úkol. A podle mého soudu jde část této obtížnosti na vrub skutečnosti, že komplexní sčítání „žije“ v kartézských souřadnicích, zatímco komplexní násobení „žije“ v souřadnicích polárních (jak jsme právě viděli). A tyto dvě souřadnicové soustavy jako by byly z jiného světa. Jedna z Marsu a druhá z Venuše.

A pokud mi dovolíte domlátit tuhle lacinou analogii až na samou dřeň její existence - jak by řekl jiný básník - uzavřu tuto podsekci nekorektní genderovou hypotézou, že muži přemýšlejí v soustavě kartézské, zatímco ženy v soustavě polární. Haha, zasmáli se zbrojnoši...

+++++++++

(a ještě něco pro příznivce sinu a kosinu)

Z Eulerovy rovnice (8) se dá odvodit i zajímavý vztah mezi exponenciálou a goniometrickými funkcemi (který v reálné analýze vůbec není vidět). Napíšeme si ji jak pro kladný, tak záporný úhel x:

exp(ix) = cos(x) + i sin(x)
exp(-ix) = cos(-x) + i sin(-x) = cos(x) - i sin(x)

sečtením a odečtením těchto rovnic dostaneme tyto vztahy:

cos(x) = (exp(ix) + exp(-ix)) / 2
sin(x) = (exp(ix) - exp(-ix)) / (2i)

Ty můžeme považovat za definici komplexních goniometrických funkcí (protože žádné trojúhelníky s komplexními úhly v praktickém životě stejně nenajdeme). Pokud si ze školy pamatujete definici funkcí sinh (hyperbolický sinus) a cosh (hyperbolický kosinus), najdete v jejich vzorečcích jistou podobnost:

cosh(x) = (exp(x) + exp(-x)) / 2
sinh(x) = (exp(x) - exp(-x)) / 2

To vlastně znamená, že z pohledu komplexních čísel jsou goniometrické a hyperbolické funkce prakticky jedno a to samé. Stačí vyměnit x za ix.

cosh(x) = cos(ix)
sinh(x) = i sin(ix)

Pokud si vzpomenete, že násobení íčkem odpovídá pootočení o 90 stupňů, můžeme se na hyperbolický kosinus z pohledu komplexní analýzy dívat jako na „běžný“ kosinus pootočený o 90 stupňů. Hodnota hyperbolického kosinu, řekněme, v bodě z = 2 + i je tedy to samé, co hodnota kosinu v bodě pootočeném o 90 stupňů, což je iz = i(2 + i) = -1 + 2i. Takže suma sumárum:

cosh(2 + i) = cos(-1 + 2i).

Jak jsem poznamenal výše, grafy komplexních funkcí jsou trochu komplikované, ale kdybyste někdy potkali čtyřrozměrného mimozemšťana, který by měl k dispozici graf komplexního kosinu vymodelovaný třeba na dřevěné desce, tak graf hyperbolického (komplexního) kosinu byste si mohli prohlédnout tak, že byste jeho dřevěnou desku prostě pootočili o 90°.

Tohle ukazuje na velkou sjednotitelskou roli komplexní analýzy. Goniometrické i hyperbolické funkce jsou si zde navzájem sourozenci (obě skupiny jsou jen kombinacemi komplexních exponenciál). Z pohledu reálné analýzy taková souvislost obou kosinů (a sinů) není vidět.

Možná si ze střední školy vzpomenete, že funkce sin a cos popisují pohyb bodu po kružnici, zatímco jejich hyperboličtí bratři, sinh a cosh, popisují pohyb bodu po hyperbole (na obrázku níže vidíte příslušné kartézské souřadnice těch bodů). Pokud si ty funkce vykreslíte na grafické kalkulačce, budou se vám reálně jevit jako dvě dvojice zcela nesouvisejících funkcí, přestože jedny jsou jen pootočením těch druhých v komplexní rovině (jak jsme právě viděli).

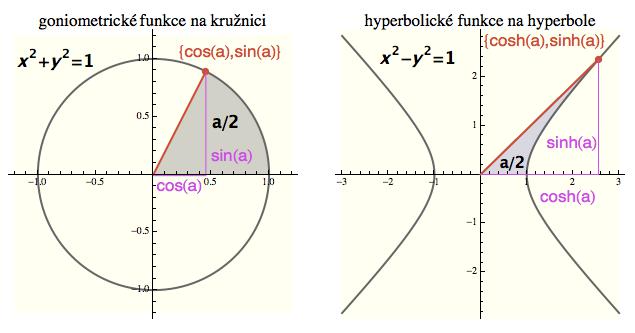
Ten parametr a má v obou případech stejný význam - je to dvojnásobek vystínované plochy. To v případě kružnice (vzpomenete-li si na vzoreček pro obsah kruhové výseče) přesně odpovídá úhlu v počátku - jak jsme viděli výše. U hyperboly by vám to s tím úhlem ale neprošlo (více podrobností najdete zde).

Mimochodem to, že ryze imaginární exponenciála popisuje pohyb po kružnici, se dá vysvětlit i jinak - trochu fyzikálněji. Představte si, že t je čas a my sledujeme pohyb bodu, jehož poloha v rovině je dána výrazem exp(it). To znamená, že v čase nula má náš bod polohu {1,0}, což je souřadnicové vyjádření pro exp(0)=1+0i. Pro derivaci reálné exponenciály platí, že (exp(at))' = a exp(at), takže pokud ta komplexní exponenciála má být co k čemu, měla by splňovat totéž: (exp(it))' = i exp(it). To ale znamená, že náš bod se pohybuje tak, že vektor jeho rychlosti (levá strana) je vždy kolmý na vektor polohy (pravá strana), protože - jak jsme viděli výše - násobení íčkem vytváří kolmý vektor. Takže hledáme křivku, jejíž tečný vektor (rychlost) je kolmý na vektor polohy. A to se dá udělat dvěma způsoby - buď si sestavíme diferenciální rovnici, ze které skutečně dostaneme, že hledanou křivkou je jednotková kružnice, a nebo si vzpomeneme ze střední školy na poučku, že právě kružnice má tu vlastnost, že její tečný vektor je kolmý na vektor polohy (což je zde radius-vektor).

+++++++++

Sekce Jauvajs: Komplexní logaritmus

jen pro mimořádně otrlé povahy

Logaritmus je inverzní funkcí k exponenciále. Jeho reálná verze je celkem jednoduchá - je to funkce všude rostoucí, všude konkávní, žádné lokální extrémy nemá, zkrátka studenta u zkoušky s ní moc nepotrápíte. Komplexní logaritmus je naproti tomu pěkně protřelý prevít. Abychom jeho vrtochy pochopili, musíme si nejprve na komplexní exponenciálu pořádně posvítit.

Následující dvojobrázek ukazuje, jak exponenciála zobrazuje vstupní hodnoty (in) na výstupní (out). Připomeňme si její formulku:

exp(x + iy) = exp(x) * exp(iy)

Jak jsme zjistili v předešlé sekci, výraz napravo je de facto polární formou komplexního čísla. Výraz exp(x) nám udává poloměr (pro každé x je to kladné číslo) a exp(iy) je bod na kružnici, odpovídající polárnímu úhlu y.

Nejprve se podívejme na ten uzoučký růžový proužek kolem osy x (jeho šířka odpovídá rozmezí od -π do π na ose y). Každá z naznačených vstupních úseček (které mají konstantní x) se na výstupu exponenciály zobrazuje na kružnici o poloměru exp(x). Pro záporná x bude hodnota exp(x)<1, takže kružnice je stěží vidět, ale jak se x zvětšuje, poloměr příslušných kružnic roste také. Když v duchu pro každou úsečku projedete s hodnotou y od -π do π (tedy od spodního okraje proužku k tomu vrchnímu), na kružnici tomu bude odpovídat úhlový pohyb od -π do π (tedy od -180° do 180°).

Odvážnější jedinci si mohou představit, jak by exponenciála zobrazovala přímky horizontální (tedy kolmé na ty vyznačené úsečky). Pro ně bude y konstantní, takže ten druhý člen v definiční rovnici nahoře bude odpovídat konstantnímu úhlu, a když v duchu projedete s x od minus nekonečna do plus nekonečna, tak ten první člen proběhne od 0 do nekonečna. To znamená, že obrazem takové přímky bude v rovině výstupní (out) paprsek směřující z počátku pod úhlem y (kde y je dané vstupní přímkou).

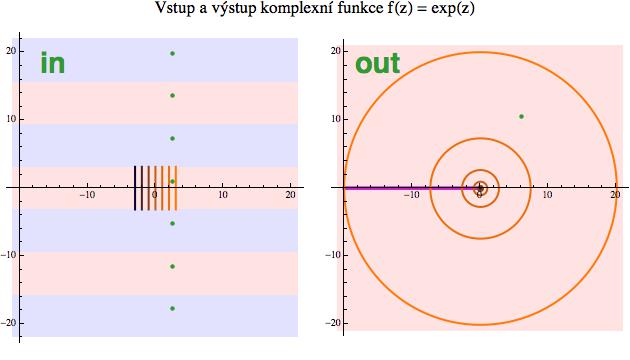
(na tomto obrázku vidíte, jak exponenciála převádí kartézské souřadnice na polární)

Důležité je uvědomit si, že zatím mluvíme pouze o tom prostředním růžovém proužku. Z diskuse výše vyplývá, že exponenciála zobrazuje tento proužek (vlevo) na celou komplexní rovinu (vpravo) s výjimkou bodu 0 (!). Komplexní exponenciála - stejně jako ta reálná - nemá žádný kořen, to znamená, že žádné číslo (ani reálné, ani komplexní) nedokáže zobrazit do nuly.

Ostatní proužky vlevo už tedy nic nového nepřinášejí, pouze opakují hodnoty, které už jsme jednou viděli. To si můžete ověřit tak, že podél jedné úsečky nalevo budete v duchu pokračovat dál do vyšších a vyšších proužků. Odpovídající obraz (napravo) takového pohybu bude bod neustále obíhající podél příslušné kružnice (jejíž poloměr je určen hodnotou x dané úsečky). To je opět důsledkem toho, že exponenciála má periodu 2πi (2π je šířka každého proužku).

Opakování hodnot je na obrázku ilustrováno zelenými body (vlevo), které se všechny - bez rozdílu - zobrazují do jediného zeleného bodu vlevo. To samozřejmě při definici inverzní funkce způsobuje velký problém, protože není jasné, který z těch bodů vlevo bychom měli inverzní funkci (a to je komplexní logaritmus) vlastně přiřadit.

Tato nejednoznačnost se ošetří úplně stejně jako při konstrukci inverzní funkce k sinu (a to je arcsin). Tam jsme prostě definiční obor zúžili tak, aby se nestalo, že by dvěma různým hodnotám x odpovídalo stejné y. Tady uděláme to samé. Prostě si ze všech těch proužků vybereme jen jeden a na ten naši exponenciálu omezíme. V každém takovém proužku je zelený bodík pouze jeden, takže inverzní trpaslík nebude mít s přiřazením potíže.

V praxi si samozřejmě vybereme skoro vždycky ten prostřední růžový proužek, ale ve speciálních případech si můžeme vybrat i jiný, exponenciálu omezit na něj a dostaneme pak trochu jiný logaritmus - technicky říkáme, že dostaneme jinou „větev logaritmu“.

Pokud se tedy omezíme jen na prostřední růžový proužek, dostaneme tzv. hlavní větev logaritmu a pro ni si odvodíme celkem jednoduchou rovnici. Vyjádříme si číslo w (v pravé části obrázku) v polárních souřadnicích w = r*exp(ia) a budeme hledat, jaké číslo z = x+ iy (vlevo) se nám do tohoto bodu zobrazí. To bude logaritmus čísla w. Podle diskuse na začátku sekce, je exp(x) = r, takže dostaneme x = ln(r). Polární úhel a bude přímo odpovídat hledanému y (viz definiční rovnice exponenciály). Pro komplexní logaritmus tak dostaneme poměrně snesitelný vzoreček:

log(w) = ln(r) + ia = ln(Abs(w)) + i Arg(w)

kde jsem použil značení pomocí absolutní hodnoty (což je de facto polární poloměr) a argumentu (polární úhel) čísla w. A protože je jedno, jaká písmenka pro značení používáme, přejdeme v definici inverzní funkce k běžnějšímu z:

log(z) = ln(Abs(z)) + i Arg(z)

(ln zde značí obvyklý přirozený logaritmus reálných čísel)

+++++++++

Na problém s jednoznačností se teď můžeme podívat i z druhé strany - tedy ze strany logaritmu. Představte si, že v pravé části obrázku pochodujete podél jedné z polárních kružnic a průběžně počítáte logaritmus čísla, ve kterém se nalézáte. Reálná část logaritmu nepředstavuje problém, protože na kružnici je absolutní hodnota konstantní, takže si v té formulce výše moc nezapočítáte. Musíte ale dávat pozor na polární úhel, který určuje imaginární složku (a počítejme to pro jednoduchost ve stupních, i když v tom logaritmu to samozřejmě musíte udat v radiánech). Takže vystartujeme ze záporné osy x (na obrázku fialově) s úhlem -180°. Jak postupujeme proti směru hodinových ručiček, úhel nejprve utěšeně klesá -170°, -160°, -150°..., ale pak přelezeme kladnou osu x a za ní nám opět začne narůstat 0°, 10°, 20°...

Jenže až celou kružnici obejdeme (a začneme se opět blížit k záporné ose x), úhel začne nabývat hodnot 160°, 170°, 180° - a tady stop! Dál nemůžeme. Kdybychom postupovali dál podél kružnice, dostali bychom se tam, kde už jsme jednou byli, a úhel by nám najednou začal nesouhlasit s tím předchozím nálezem - my ten úhel v komplexním logaritmu nemůžeme jednou definovat jako -170° a podruhé jako 190°. Funkce musí jednomu vstupu - jednomu bodu na kružnici - přiřadit pouze jeden výstup. A tady bychom pro jedno komplexní číslo z (na kružnici kousek pod fialovou polopřímkou) dostali dva různé úhly - a tedy dvě různé hodnoty logaritmu. V reálném případě je tato funkce definována prostě jen na jedné polopřímce z nuly (kladná osa x), takže tam žádné problémy s polárním úhlem nevznikají.

Tato patálie se dá vyřešit dvojím způsobem.

První možnost je, že do komplexní roviny postavíme pevnou zarážku, která nám znemožní polární kružnice procházet vícekrát. To se udělá tak, že se z počátku vyšle nějaká polopřímka (na obrázku výše vpravo je znázorněna fialově podél záporné osy x) a na této polopřímce prohlásíme komplexní logaritmus za nedefinovaný. Polopřímku z počátku si můžeme vybrat celkem libovolně, ale záporná osa x je nejčastější volbou (polární úhel pak probíhá od -180° do 180° a díky té vyhozené polopřímce se vyhneme výše popsané nespojitosti). Samozřejmě bychom také mohli vyhodit kladnou osu x, ale to bychom si zbytečně znemožnili výpočet komplexního logaritmu pro kladná reálná čísla.

Druhá, a poměrně exotická možnost spočívá v tom, že si komplexní rovinu představíme jako koberec, který rozstřihneme podél fialové polopřímky. V okamžiku, kdy se při našem pohybu podél kružnice dostaneme zpět ke 180° (a chtěli bychom pokračovat do zakázaných 190°), tak na komplexní rovinu hodíme další rozstřihnutý koberec a oba sešijeme podél fialových rozparků takto: vrchní okraj (tedy ten, který odpovídá kladným hodnotám y) rozparku na spodním koberci sešijeme se spodním okrajem (který odpovídá záporným hodnotám y) rozparku horního koberce a pak vesele pokračujeme dále, protože na koberci „nahoře“ jsme ještě logaritmus nedefinovali, takže si tam těch 190° můžeme klidně lajsnout, aniž bychom se dostali do sporu s předchozí definicí. Až se otočíme o dalších 360°, hodíme na komplexní rovinu třetí koberec, který opět sešijeme stejným způsobem, a takhle pokračujeme pořád dál, močálem temným kolem bílých skal.

Touto bizarní konstrukcí dostaneme funkci logaritmus, která bude jednoznačně definovaná ne v komplexní rovině, ale na podivné nestvůře sešité z nekonečně mnoha koberců (její struktura trochu připomíná spirálovité schodiště). Této nestvůře se říká Riemannova plocha komplexní funkce logaritmus.

Z praktického pohledu je lepší se spokojit s nespojitostí a definovat logaritmus jen mimo fialovou úsečku. Pro většinu aplikací to stačí. Mimochodem, ten (úhlový) skok, který bychom přechodem úsečky prodělali, se přenáší i na funkce z logaritmu odvozené, jako je např. druhá odmocnina, kterou můžeme vyjádřit takto:

sqrt(z) = exp(log(z)/2)

I v její definici si musíme vybrat, zda se spokojíme s nespojitostí podél nějaké vyhozené polopřímky, a nebo se pokusíme sestrojit její Riemannovu plochu. To už jsou ale poměrně náročné úlohy i pro experty, takže si s tím nebudeme lámat hlavu.

Článek je redakčně upravenou verzí blogového příspěvku na serveru iDNES.cz. Publikováno s laskavým svolením autora.

Další díly a původní texty jsou dostupné na blogu Jana Řeháčka.

Autor: Jan Řeháček