Když se matematici začali zabývat problémem, jak správně změřit délku mořského pobřeží, zjistili, že odpověď závisí na tom, jak podrobné detaily jste ochotni zkoumat. Jejich analýza vedla k zajímavému zobecnění pojmu dimenze.
Dimenze patří k těm veličinám, o kterých automaticky předpokládáme, že jsou vyjádřeny celými čísly (stejně jako třeba tvrdost tužek či počet neutronů v atomovém jádru). Pokud si dimenzi představíme jako minimální počet souřadnic, které musíme zadat k určení své polohy, jen těžko bychom hledali příklad prostředí, ve kterém musíme poskytnout 2.537 souřadnic, aby nás policejní vrtulník rychle dohledal.
Přesto se ukázalo, že existují objekty, jejichž dimenze se dá celkem přirozeně vyjádřit číslem desetinným. Na počátku úsilí o vysvobození dimenze z celočíselného krunýře ale nestála nějaká hlubokomyslná úvaha o povaze vektorového prostoru, ale zdánlivá nemožnost precizně změřit délku mořského pobřeží. Inu, cesty matematiky jsou nevyzpytatelné.
V roce 1950 se anglický matematik, meteorolog, pacifista a psycholog, Lewis Fry Richardson, zabýval korelací mezi pravděpodobností válečného konfliktu dvou sousedních zemí a délkou jejich společné hranice. Když začal zkoumat data, zjistil fascinující věc. Údaje o délce společné hranice se často rozcházely až o několik stovek kilometrů. A není těžké zjistit proč. Mapy mají různé měřítko a na jeho základě pak věnují či nevěnují pozornost drobným odchylkám v oscilacích klikaté hraniční čáry. A podle toho, kterou mapu použijete, pak dostanete různé výsledky.
Na Richardsonův téměř zapomenutý výzkum navázal v 70. letech francouzský polyhistor Benoit Mandelbrot, který ukázal, že ještě naléhavěji tento problém vystupuje při měření přirozených hranic, které nejsou svázané lidskou tendencí k jednoduchosti a přímočarosti. Paradox délky pobřeží se stal předmětem zájmu matematiků na celém světě a brzy se ukázalo, že jedním ze způsobů, jak tento problém uchopit, je rozšířit pojem dimenze mimo celá čísla. Objektům, které se pro svou vnitřní komplexitu nedají sešněrovat do lineární kazajky tradiční dimenze, říkáme od těch dob fraktály (tedy něco jako „zlomkáče“).
A kupodivu se ukázalo, že se nemusí nutně jednat o abstraktní matematické chiméry (jako je třeba neměřitelná množina či křivka vyplňující prostor). Fraktální povahu mají i běžné objekty, které se dají (pokud trochu slevíme z preciznosti definic) najít v přírodě.
Fraktální dimenze
Fraktální dimenze nevyplývá z jemnější analýzy vektorových prostorů, ale duchovně navazuje na Lebesgueovu dimenzi, založenou na pokrývání zkoumaného objektu otevřenými množinami.
Nepotřebuje tedy lineární strukturu a bohatě si vystačí s topologickými vlastnostmi (proto se jí také někdy říká topologická dimenze). I tato dimenze je celočíselná a není bez zajímavosti, že o její rozvoj se zasloužil významný český matematik a topolog Eduard Čech.
Abychom mohli dimenzi vystavit propustku do světa reálných čísel, budeme muset její definici trochu přeformulovat (jako když jsme se kdysi pokoušeli vymyslet desetinnou verzi faktoriálu). Podívejme se nejprve na ústřední myšlenku bez nároku na preciznost.
Základem naší úvahy bude fakt, že v různých dimenzích se míry objektů se změnou měřítka mění různým způsobem. Představme si, že máme měřicí tyčinku délky r = 1, 1/2 a 1/3. Na dalším obrázku vidíme jednotkovou úsečku, čtverec a krychli poměřované těmito tyčinkami.
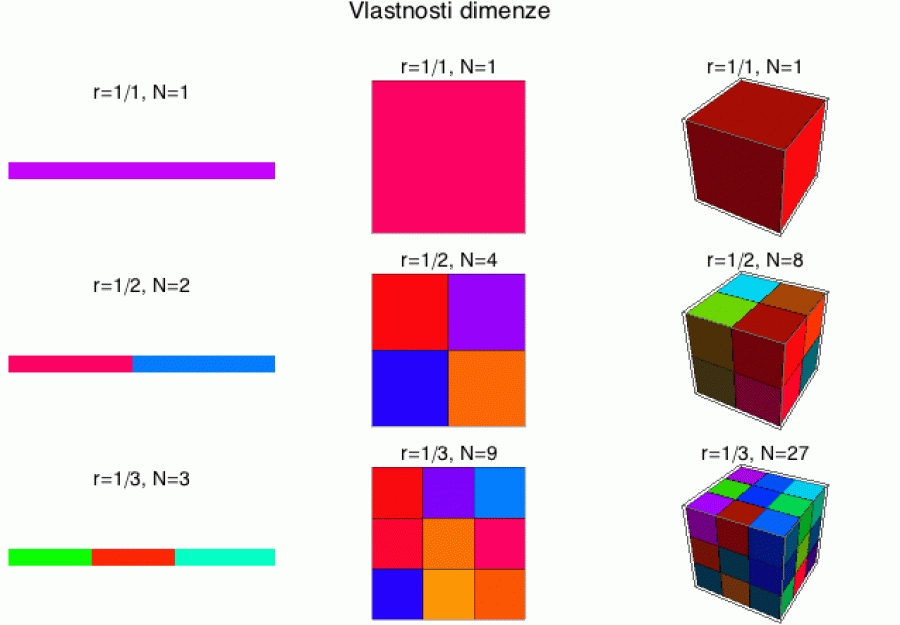
Pokud v 1D změníme měřítko na polovinu (tj. použijeme tyčinku poloviční délky), původní úsečku pokryjeme dvěma zmenšenými kopiemi. Pokud použijeme tyčinku s třetinovou délkou, vejdou se do ní tři (viz první sloupec).
Ve 2D to funguje o něco razantněji (druhý sloupec). Objekty odpovídající poloviční délce tyčinky už do původního čtverce nasázíme 4 (a v případě třetinové tyčinky 9). Ve 3D už bychom na pokrytí krychle potřebovali 8 krychliček odpovídajících polovičnímu měřítku a 27 odpovídajících třetinovému. A ve vyšších dimenzích ty mocniny dál utěšeně rostou.
Dá se tedy říci, že v d dimenzích se při změně měřítka r dá původní objekt pokrýt N zmenšenými kopiemi, kde N závisí na dimenzi takto:
1D: N = 1/r
2D: N = 1/r2
2D: N = 1/r3
Obecně v dimenzi D dostaneme:
(*) N = (1/r)^D
Na dimenzi se tedy můžeme dívat jako na exponent, který nám ukazuje, jak dostat počet pokrývajících objektů z použitého měřítka. Ve 2D budou tyto počty růst kvadraticky, ve 3D kubicky atd.
Mimochodem, měřítko r ve jmenovateli vypadá trochu neohrabaně, proto se v některých zdrojích místo něho používá škálovací koeficient k = 1/r, takže vzoreček (*) pak vypadá stravitelněji: N = k^D.
Ještě lepší je na obě strany (*) aplikovat logaritmus
log(N) = D*log(1/r) = -D*log(r)
a pak vidíme, že dimenze je vlastně konstantou úměrnosti mezi logaritmem měřítka a logaritmem počtu kopií.
Tento jednoduchý mechanismus nám umožní posoudit dimenzi množin, jejichž komplikovaná struktura nám brání nahlížet na ně jako na ohnutý kus eukleidovského prostoru (tj. varietu), ze kterého by se ta dimenze dala lehce odečíst.
Nejlépe je to vidět na množinách, které při přeškálování na jiné měřítko vykazují určitou samopodobnost. Asi nejjednodušší je tzv. Cantorova množina (už jsme se s ní jednou setkali), kterou dostaneme tak, že z jednotkové úsečky (0,1) neustále vyhazujeme prostřední třetiny. To, co nám na nejspodnější řádce zůstane po nekonečně mnoha vyhazovacích raziích, je Cantorova množina (na obrázku je zobrazeno pouze prvních 6 iterací její konstrukce).
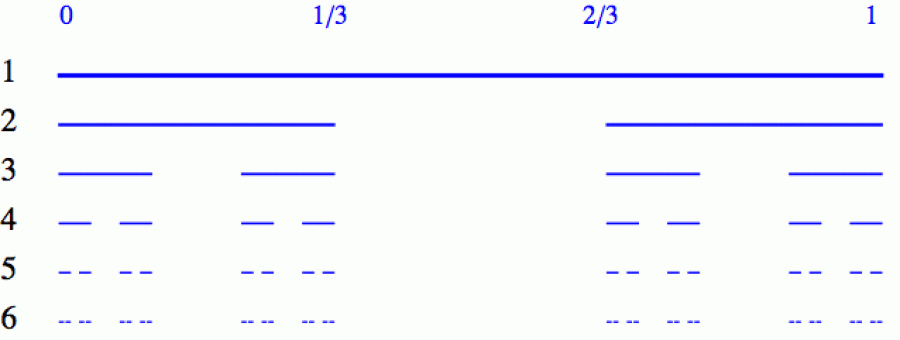
A tady vidíme jádro pudla. Zatímco u plné úsečky jsme při změně měřítka (r = 1/3) potřebovali tři menší kopie na pokrytí množiny, tady nám stačí pouze dvě (tu prostřední kopii vždy vyhodíme). Pokud tedy zmenšíme měřicí tyčinku v každém kroku na třetinu (r = 1/3), dostaneme pouze N = 2 nové kopie, ze kterých se naše množina na dané úrovni skládá. Budeme-li se na dimenzi dívat jako na poměr mezi logaritmem měřítka a logaritmem počtu kopií, kterými lze množinu pokrýt, pak nám vyjde
log(2) = D log(3)
a dimenze Cantorovy množiny bude rovna
D = log(2) / log(3) = 0.63
To celkem odpovídá naší intuici, že výsledná Kantorova množina (to jemné smetí, které bychom dostali, pokud bychom za 6. řádkou pokračovali dál do nekonečna) je o něco méně než plný 1D interval, ale zase podstatně více než jen pár osamělých 0D (nulodimenzionálních) bodíků – koneckonců Cantorova množina i přes všechny ty razie obsahuje nespočetně mnoho bodů a dá se vzájemně jednoznačně zobrazit na kompletní interval (0,1).

Dalším klasickým příkladem tohoto způsobu počítání dimenze je tzv. Kochova vločka (obr. vpravo).
I zde začneme poměrně jednoduchým útvarem – rovnostranným trojúhelníkem – na který budeme aplikovat nekonečnou sekvenci určitých transformací. Podobně jako u Cantorovy množiny vyhodíme z každé strany prostřední třetinu, ale tentokrát ji nahradíme dvěma stranami příslušného rovnostranného trojúhelníku (proto obvod naší množiny nebude ubývat, ale bude naopak pomalu růst).
Na horním obrázku si zvolíme měřicí tyčku odpovídající celé straně a nastartujeme přeměřovací proces. V první etapě nám vyjde 3 a všechny ostatní detaily na této úrovni zanedbáme. A teď budeme zkoumat, co se bude dít, když začneme tyčinku zkracovat. Kdykoliv ji ořízneme na třetinu a přeměříme obvod, jeho délka se pronásobí faktorem 4/3. V každém kroku jsme totiž ze tří třetin našlehali čtyři (tu prostřední jsme nahradili dvěma úsečkami stejné délky, takže na rozdíl od předchozího případu nedostaneme třetiny 2 ale hned 4).
Při změně měřítka na r = 1/3 se tedy do objektu vejdou N = 4 kopie měřicí tyčinky a fraktální dimenze Kochovy vločky bude D = log(4)/log(3) = 1,26. Ta vločka se prostě neustále vrtí a na všech škálách vybíhá kolmo na svůj 1D směr, takže její fraktální dimenze je o něco větší než 1.
Dalším efektem této konstrukce je skutečnost, že výsledná Kochova vločka – přestože se jedná o množinu s konečným obsahem – má nekonečnou délku (přesněji obvod). V každé iteraci se její délka násobí konstantním faktorem 4/3.
Z těch obrázků vpravo krásně vidíte, proč je takovým problémem stanovit délku pobřeží (či obecněji hranice). Na každé úrovni měření se díváme na různé rozlišení detailů (viz obrázek na wiki) a to nás může dovést k různým hodnotám (ba v limitě dokonce až k nekonečnu).
Naštěstí ne všechny objekty vykazují takové patologické chování. Pro většinu slušně vychovaných útvarů tento proces přeměřování na zmenšujících se škálách konverguje k hodnotám obvodu, které známe ze školy.
Kantorova množina i Kochova vločka patří k nejznámějším příkladům fraktálů. Protože jsou vytvořené pomocí poměrně jednoduchých pravidel, jejich dimenze se dá určit přesně – vyplývá z jejich samopodobnosti: tedy z toho, že jednotlivé součásti opakují určité vzorce chování, jen na jiné měřicí škále.
Fraktály najdeme velmi často mezi atraktory diskrétních dynamických systémů (viz toto Matykání). Speciálním případem jsou pak Mandelbrotova a Juliova množina, jejichž tvar je odvozen z chování atraktorů v komplexní rovině. U nich už se dimenze stanovuje hůře.
Proces popsaný v této sekci je obecná myšlenková kostra, na jejímž půdorysu je postaveno hned několik definic fraktální dimenze. Podívejme se na dvě konkrétní varianty.
Minkowského dimenze
Když to shrnu, tak v minulé sekci jsme viděli, že pojem dimenze se dá rozšířit pečlivým sledováním procesu pokrývání dané množiny stavebními bloky různých rozměrů. Pokud se zdá, že logaritmus počtu takových bloků je přímo úměrný logaritmu „velikosti“ těchto bloků, pak se na konstantu úměrnosti (opatřenou minusem) můžeme dívat jako na zobecnění tradičního pojmu dimenze.
V uvedených příkladech jsme pokrývací výpočet mohli pro speciální hodnoty měřítka (r = 1/3) provést zcela přesně díky samopodobnosti dané množiny. Pakliže se nemůžeme opřít o nějaké geometrické vztahy, provedeme (v rámci možností) co nejvíce měření a výslednou dimenzi D z nich pak vydyndáme pomocí limitního procesu anebo nějakého regresního mechanismu („proložením přímky“). Asi nejjednodušší implementací tohoto procesu je Minkowského dimenze, které se pro její jednoduše představitelný princip říká „dimenze počítání krabic“ (box counting dimension).
Vezměme si nějakou množinu M v n-rozměrném eukleidovském prostoru R^n (prostor, ve kterém množina M „sedí“, je v průběhu celé operace zafixován). Pomocí pravidelné mřížky ho rozřežeme na n-rozměrné „krychličky“ o rozměru r (ve 2D to tedy budou čtverečky o straně r) a spočítáme ty, které naše množina M protíná.
Označíme-li si jejich počet N(r), pak pro Minkowského dimenzi množiny M platí
dim(M) = lim log(N(r)) / log(1/r) = - lim log(N(r)) / log(r) (kde limita naznačuje chování podílu pro hodnoty r zmenšující se k 0)
Samozřejmě, ne vždy máme k dispozici bohatá data (nebo jednoduchý model), abychom si mohli nabrnkat dostatečně hodnot r, ze kterých by se limita (a tedy dimenze) dala spočítat nebo alespoň odhadnout.
Při odhadu fraktální dimenze pobřeží z nějakého obrázku pracujeme pochopitelně s konečným rozlišením, takže se dříve či později dostaneme na úroveň pixelu a ten už rozřezat na menší krychličky nemůžeme. Navíc je pobřeží (na rozdíl od Kochovy vločky) většinou nepravidelné a nemůžeme spoléhat na to, že přesně „uhodneme“ mechaniku skládání detailů při zmenšování měřítka. Pokud je ale obrázek dostatečně podrobný, můžeme těch měřicích škál r prubnout několik a z takto obdržených hodnot spočítat regresní přímku.
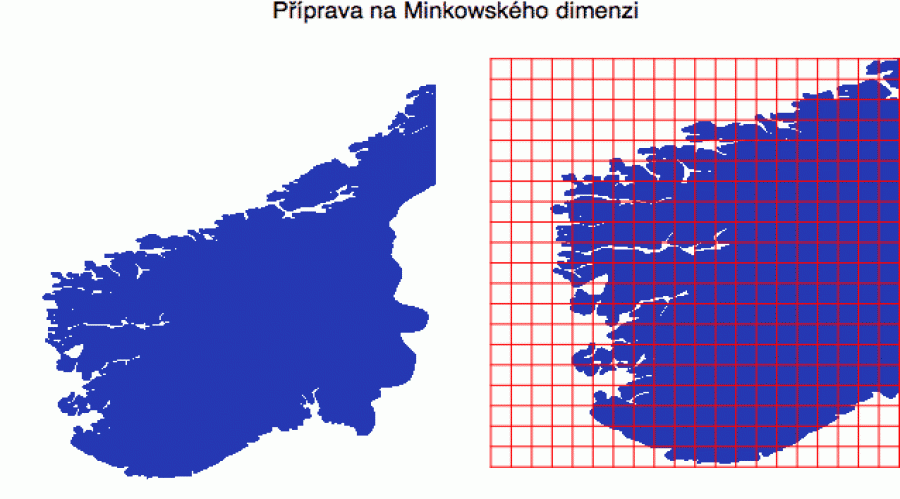
Tady máme kus norského pobřeží, které už od pohledu vypadá jako fraktál (odborně říkáme, že mu to „kouká z očí“). Zkusme si odhadnout jeho fraktální dimenzi pomocí Minkowského formulky (zde budeme pracovat v R2). Za tím účelem obrázek rozřežeme na malé čtverečky o rozměru r a budeme sledovat, kolik z nich obsahuje naše pobřeží.
Obrázek převedeme na matici pixelů a díky tomu, že pracujeme v modrobílé verzi, každý pixel je buď 1 (modrá), nebo 0 (bílá). Rozbít takovou matici na malé minimatice (reprezentující jednotlivé čtverečky) není pro počítač žádný problém a nám už pak zbývá jen spočítat ty, které obsahují jak jedničky, tak nuly – ty odpovídají hranici naší množiny (tedy danému pobřeží). Čtverečky, které jsou úplně bílé či úplně modré, nás nezajímají (tam pobřeží není – tam je buď jen voda, nebo jen pevnina).
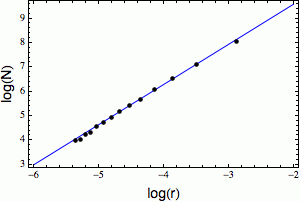
Nakonec si pro každý rozměr mřížky r ty mixované čtverečky spočítáme a číslo N(r) vyneseme do grafu (viz obrázek vpravo).
Vidíte, že úplně přesně v lajně body neleží (to se u nematematických fraktálů ani nedá očekávat), ale také se od té (modré) regresní přímky moc neodchylují. Její rovnice (spočítaná metodou nejmenších čtverců) je log(N) = 12 + 1.5*log(r).
Konstanta úměrnosti mezi oběma logaritmy je tedy cca 1.5 a to je fraktální dimenze norského pobřeží (konstanta 12 zde nehraje žádnou roli – v rovnici (*) nás zajímá exponent, ne případný multiplikátor).
Pokud máte software, který dokáže s obrázkem manipulovat na úrovni pixelů, můžete si odhadnout fraktální dimenzi rozvětvených stromů, mořských pobřeží, rozčepýřených vlasů a čehokoliv jiného (zajímavou ukázku fraktálovitých útvarů v geomorfologii naší planety naleznete zde).
Z pohledu matematiky má však Minkowského dimenze několik much. Například racionální čísla na intervalu (0,1) mají dimenzi 1 (tedy stejnou jako celý interval), protože ten interval hustě pokrývají (v racionálních číslech nejsou žádné „mezery“). Těch pokrývacích čtverečků (zde vlastně interválků) o rozměru r budeme potřebovat úplně stejně mnoho jako na pokrytí celého intervalu.
To se matematikům moc nelíbilo, protože racionální čísla jsou de facto spočetnou kolekcí 0-dimenzionálních bodíků a měly by mít tedy menší dimenzi než 1. Nabízí se analogie s celými čísly: to je také kolekce spočetně mnoha 0-dimenzionálních bodíků a těm bychom intuitivně přiřadili spíš dimenzi 0 než 1.
Proto si matematici sestrojili další verzi fraktální dimenze, kde už mají racionální čísla pouze dimenzi 0. Tu máš čerte kropáč!
Hausdorffova dimenze
(připomeňme si ze staršího
Matykání, že v matematice je slovo „míra“
zastřešujícím výrazem pro délky, obsahy a objemy – podle toho v jaké se
nalézáme dimenzi)
Hausdorff implementuje myšlenku fraktální dimenze trochu jiným způsobem – dívá se na ni prizmatem míry. Objekty mají smysluplně definovanou míru pouze, když ji aplikujeme ve správné dimenzi. Podívejme se na funkci, která umí spočítat 3D míru (můžete si ji nahrubo představit jako skříňku s trpaslíkem: na vstupu do ní vložíte nějaký objekt X, trpaslík ho ponoří do kýblu s vodou, podívá se, kolik vody to vytlačilo, a na výstupu vám vyhodí nezáporné reálné číslo, vyjadřující objem objektu X).
Vhodíme do ní bod, vypadne nám nula (bod nemá žádný objem). Vhodíme do ní kus přímky nebo roviny, vypadne nám zase nula (ani 1D nebo 2D objekty nemají žádný objem). Teprve když do ní vhodíme něco opravdu 3D, třeba bramboru, vypadne nám kladné číslo (objem brambory).
Funkce počítající 2D míru (obsah) by reagovala podobně: vhodíme do ní bod nebo kus přímky, vypadne nám nula (bod i přímka má nulový obsah). Hodíme do ní bramboru, vypadne nám nekonečno (bramboru můžeme rozřezat na nekonečně tenké plátky, jejichž celková 2D plocha bude nekonečno). Teprve kdybychom do ní hodili nějaký veskrze 2D objekt, řekněme trojúhelník nebo kruhovou výseč, vypadl by nám rozumný obsah.
Všimněte si, že pojmy dimenze a míry jsou určitým způsobem sladěny. Každá míra jakoby rezonovala pouze s objekty určité dimenze D a pouze pro tuto hodnotu dávala smysluplná čísla (pro všechny ostatní objekty bude vyhazovat buď nulu, nebo nekonečno).
Hausdorffova dimenze je postavena přesně na této rezonanci, jen se na ni dívá jaksi z druhé strany. Zatím jsme měli jednu míru (funkci), do které jsme vhazovali různé objekty. Hausdorff si sestrojil různé míry (funkce) – jednu pro každé nezáporné reálné číslo d (což nemusí být celé číslo!) – a do těch funkcí bude vhazovat jeden jediný objekt: množinu, jejíž dimenzi se pokouší změřit. Pak si vytáhne rezonující skříňku, podívá se vzadu na její etiketu, kde je vyražena hodnota d, a Hausdorffova dimenze je na světě.
(subscript budu značit podtrhovátkem: H_d je tedy H s indexem d)
To, co každá funkce pro danou množinu M vyprodukuje, tedy Hausdorffovu míru dimenze d, si označíme symbolem H_d(M). Než se ale zamotáme do detailů všech těch pozoruhodných měr H_d, podívejme se podrobněji, jak z těch etiket vykouzlíme dimenzi.
Vezmeme si množinu M, která má (zatím neznámou) dimenzi D. Výše jsme si řekli, že pokud danou množinu M poměřujeme mírou H_d, jejíž definiční dimenze d je o něco vyšší, tj. D<d, pak její míra bude H_d(M) = 0. Zrovna tak jako když hodíte 1D úsečku do funkce H_2, měřící 2D obsahy. Naopak kdybychom množinu M hodili do funkce H_d, kde d<D, pak by její míra byla H_d(M) = ∞, zrovna tak, jako když jsme 3D bramboru hodili do funkce H_2.
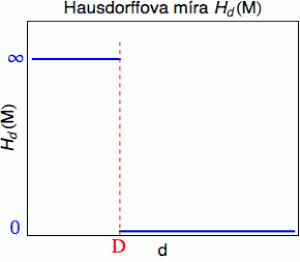
Ta Hausdorffova míra H_d tedy funguje tak, že je nejprve chvíli nekonečná (pro malé hodnoty d), pak v jistém okamžiku skočí střemhlav do nuly a v ní pak setrvá až do skonání věků (viz ilustrační obrázek vpravo – pro jednu zafixovanou množinu M). Ten skok bude náš indikátor „rezonance“. Hodnota H_D(M) sama o sobě může být buď nula, nebo nekonečno, anebo cokoliv mezi tím.
Tu Hausdorffovu dimenzi D teď můžeme definovat buď jako maximum hodnot d, pro které je míra H_d(M) nekonečná, anebo jako minimum hodnot d, pro které je H_d(M) rovna nule.
Hausdorff si vybral tu druhou možnost. Jeho dimenze dimH je tedy nejmenší číslo d≥0 takové, že H_d(M) = 0:
D = dimH(M) = inf {d≥0, H_d(M) = 0}
(zde inf značí infimum, což je sofistikovanější verze minima s tím, že ho daná množina nemusí nutně nabývat – např. otevřený interval (0,1) má infimum 0, přestože žádný jeho prvek se nule nerovná a nedá se tedy označit jako nejmenší – pokud vás to otravuje, klidně si v té definici představte min místo inf)
K úplné spokojenosti už nám zbývá jen vypátrat, jak se ty kouzelné d-dimenzionální míry H_d vlastně definují.
Jelikož je to poměrně zapařená záležitost, trochu to ošulím a podám vám pouze hrubou zkratku. Zájemci o krvavé detaily se mohou podívat na Wikipedii anebo si přečíst výborný technický článek, jehož autorem je jeden z nejlepších současných matematiků, Terence Tao.
Protože k tomu paření nebudeme potřebovat lineární strukturu, ale pouze pojem vzdálenosti, zapomeneme na vektorové prostory a celou operaci provedeme v nějakém abstraktním metrickém prostoru X (klidně si ho představujte jako běžný R2).
Pokud řeknu koule se středem x∈X a poloměrem r>0, mám na mysli množinu
B(x,r) = {y ∈ X , dist(x,y) < r} (kde dist je vzdálenost bodů)

V naší zjednodušené verzi začneme tím, že množinu M, jejíž dimenzi hledáme, řekněme jižní pobřeží Norska (viz obrázek vpravo), pokryjeme soustavou malých koulí s poloměry r_i < r (podobně jako jsme to udělali u Minkowského dimenze s malými krychličkami). Zde připouštíme možnost, že koule mají různé poloměry, ale všechny r_i musí být menší než nějaké pevné r (tady je podrobnější obrázek pro pobřeží Británie).
Výpočet provedeme ve dvou krocích. Nejprve si (pro to pevné r) spočítáme nejmenší hodnotu (infimum) součtu d-tých mocnin všech poloměrů r_i pro všechna možná pokrytí množiny M koulemi B(x_i,r_i). To bude taková hausdorffovská „předmíra“ S_d.
S_d(M,r) = inf {(r_i)^d, kde r_i<r jsou poloměry koulí B pokrývajících M}
Tohle je mimochodem ten okamžik, kdy jsme schopni opustit celá čísla a definovat míru pro libovolné d>0 (poloměr lze totiž umocnit na libovolné kladné číslo – r^d má smysl i pro neceločíselné exponenty).
Když si odmyslíme různé technické finesy, zjistíme, že v zákulisí se definice „předmíry“ opět odkazuje na známý fakt, že pro 1D kouli je míra úměrná r, pro 2D je úměrná r2, pro 3D r3 a tak dále. A tím, že jsme tu dimenzionalitu přesunuli do exponentu, tak jsme ji zbavili okovů celých čísel (!).
A teď druhý krok. D-dimenzionální „předmíra“ S_d(M,r) ještě stále závisí na r (což je horní tolerance pro poloměry našich kuliček), a proto ho z ní vyždímáme limitním procesem. Pro danou množinu M si spočítáme S_d(M,r) pro několik stále se zmenšujících hodnot r a podíváme se, k čemu se to blíží. Hausdorffova míra M bude potom příslušnou limitou tohoto „blížení“:
H_d (M) = lim S_d (M,r) (pro r → 0)
Sečteno a podtrženo: pokryjeme množinu M kuličkami s poloměrem menším než r, tak aby součet d-tých mocnin těchto poloměrů měl nejmenší možnou hodnotu a pak se podíváme, co se s těmi součty děje, když r zmenšujeme k nule. A to je celá Hausdorffova míra H_d(M).
Hausdorffova dimenze množiny M je pak ta hodnota d = D, pro kterou její Hausdorffova míra H_d(M) přeskočí z nekonečna do nuly.
Ten mírový proces ale moc míru do našich myslí nevnese. Celočíselná dimenze sice dostala zaslouženě po čuni a skončila zdrátovaná na chirurgii, ale pro praktické počítání je ta Hausdorffova konstrukce velmi těžkopádná (a to jsem ji ještě dost zjednodušil). Naštěstí Minkowského definice vede v mnoha případech ke stejnému výsledku, takže se dá použít v praxi jako hrubý odhad fraktální dimenze. V teoretických úvahách ale převládá definice Hausdorffova.
Seznam nejznámějších fraktálů (podle Hausdorffovy dimenze)
Článek je redakčně upravenou verzí blogového příspěvku na serveru iDNES.cz. Publikováno s laskavým svolením autora. Další díly a původní texty jsou dostupné na blogu Jana Řeháčka.