Bez kořenů se neobejde nejen rozložitý dub či národní kultura, ale ani slečna Matematika. Při cestě za kořeny se dnes seznámíme se dvěma vyššími funkcemi, které hrají v matematickém skleníku roli vzácných orchidejí.

Často se setkávám s lidmi, kteří žasnou, jak může vlastně někoho bavit tak suchopárná činnost, jako je matematika. Cožpak není psaní filmových scénářů, slepování nanorobotů anebo navrhování operních budov na mořském pobřeží daleko zábavnější než počítání nějakých zapařených integrálů, determinantů či směrodatných odchylek?

A mají pravdu v tom, že počítání samo o sobě opravdu žádná velká legrace není. To, co dělá matematiku zajímavou, je že při jejím studiu objevujete konstrukční schéma kvantitativního světa a přitom tu a tam zakopnete o zcela nečekané souvislosti. Jako by před vámi pánbůh otevřel kapotu té naší vesmírné káry a vy najednou vidíte, že tahle rozvodná skříňka je propojená kablíkem s tamtím alternátorem a že tenhle klínový řemen pohání tamto soukolí. To jsou věci, které si běžný smrtelník při řízení často ani neuvědomí, protože musí sledovat provoz a blikající kontrolky na palubní desce, a na to, co se děje v podkapotí, nemá čas.

Dneska se na jednu takovou zajímavou souvislost podíváme. Ukážu vám klikovou hřídel, která spojuje zdánlivě nesouvisející svět trojúhelníků se světem faktoriálů. Ale zadarmo to nebude. Nejprve se budeme muset prokousat několika nezbytnými technikalitami.

Tak rychle do toho a sqrt(1/4) je hotovo.

(první tři sekce můžete přeskočit - to je jen opáčko)

Pleteme si funkce hladce i obrace

Protože většina procesů v přírodě probíhá v režimu postupné změny, přirozeným nástrojem pro jejich popis jsou spojité funkce (viz 15. díl Matykání). Spojité funkce ale nejsou dostatečně jemným mechanismem, protože nedokáží odhalit „drcnutí“, a tak tento pojem nejprve trochu zpřesníme. „Drcnutí“ je proces, při kterém nedojde ke skokové změně stavu, ale ke skokové změně ve směřování procesu. Vlastnost, která takový typ změny popisuje, se jmenuje „hladkost“.

Podívejme se na následující trojici obrázků. Ten modrý ukazuje funkci, která se mění hezky postupně a předvídatelně (jak to v přírodě většinou chodí). Takovým funkcím říkáme hladké. Červená funkce je sice také spojitá (její graf lze stále nakreslit jedním tahem), ale uprostřed vidíte, že do kreslicího zařízení někdo „drcnul“. Pokud si představíte, že podél grafu této funkce pluje loďka, tak uprostřed plavby došlo ke skokové změně směru. Jako by vám nějaký zlomyslný Poseidon „kopnul do přídě“. A poslední zelená funkce je přímo nespojitá. Tady už vám Poseidon nejen kopnul do přídě, ale ještě vaši loďku popadl za ráhno a mrsknul vás na druhou stranu zátoky.

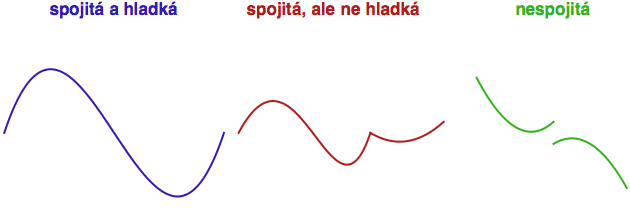
Z pohledu fyzika sledujícího naši loďku jsou důležité dvě věci: poloha (funkční hodnota) a směr pohybu (derivace). U funkcí hladkých se jak poloha, tak směr mění postupně (to znamená, že funkce i její derivace jsou obě spojité). Ztráta hladkosti pak vypovídá o skokové změně ve směřování, zatímco ztráta spojitosti indikuje skokovou změnu polohy.

Funkce, které nejsou hladké, se v přírodě tu a tam vyskytují. Představte si například výšku kamene padajícího k zemi (jako funkci času). V okamžiku dopadu ztratí funkce svoji hladkost (z paraboly se stane přímka), přestože bude stále spojitá. Funkce nespojité se v praxi vyskytují zřídka a většinou v umělých situacích (např. v ekonomice, když chcete popsat, že pro určitou hodnotu parametru najednou začnou platit nějaká nová pravidla - např. dojde ke skokovému navýšení nějakého poplatku).

Protože funkce mají také derivace vyšších řádů, dá se i hladkost ještě dále zjemnit, ale s tím si pro potřeby Matykání nebudeme lámat hlavu. Koho to zajímá, nechť si skočí sem.

Kořeny a póly

Dalším důležitým indikátorem při studiu funkcí jsou jejich kořeny (neboli nulové body). Pokud si danou funkci opět představíme jako trpaslíka v krabičce, pak kořen není nic jiného než vstupní hodnota x, pro kterou vám trpaslík na výstupu vyhodí nulu.

Pro jednoduché funkce se kořen dá celkem snadno vypočítat (v podstatě řešíte rovnici f(x)=0), ale existují i poměrně důležité funkce, pro které všechny kořeny stále ještě spočítat neumíme (viz funkce zeta na konci článku).

Jako příklad si najdeme kořeny kvadratické funkce

f(x) = 2 x² + 4 x - 6 = 2 * (x - 1) * (x + 3)

Rovnice f(x) = 0 má dvě řešení: x=1 a x=-3, které reprezentují průsečíky s osou x. Z prvního tvaru se dají spočítat kvadratickou rovnicí, z toho druhého (rozloženého na kořenové činitele) jsou vidět prostým okem.

Pól funkce je v jistém smyslu opakem kořene: je to x-ová hodnota, pro kterou je funkční hodnota rovna nekonečnu, přesněji, v jejímž nejbližším okolí se funkční hodnoty blíží nekonečnu (ať už kladnému nebo zápornému). Protože nejsnadnější způsob, jak si podomácku vyrobit nekonečno, je vydělit jedničku nulou, dohodněme se, že funkce f(x) bude mít pól tam, kde má funkce 1/f(x) kořen (tedy kde je rovna 0). A samozřejmě naopak. Tam, kde má funkce f(x) kořen, bude mít funkce 1/f(x) pól. Není to úplně nejpřesnější, ale pro potřeby Matykání nám to bude stačit.

Z grafu poznáte pól tak, že když se k němu pomalu přibližujete, tak absolutní hodnota funkce roste nade všechny meze. Na obrázku níže je pól funkce v bodě x=0. Když se k němu přibližujeme zprava, funkční hodnota roste do nekonečna, zatímco zleva klesá do minus nekonečna. Na obrázku je také zaznamenán kořen v bodě x=-1.

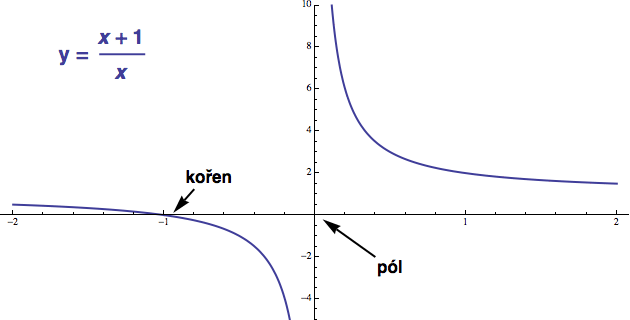
Kořen snadno spočítáme tak, že položíme f(x)=0 a dostaneme x+1=0 (zlomek je roven nule tehdy a jen tehdy, pokud je čitatel roven nule). Pól spočítáme tak, že se podíváme, kde má 1/f(x) kořen, tj. položíme 1/f(x) = x/(x+1) = 0 a máme ho: x=0 (samozřejmě ne vždy je to takto jednoduché).

Kořeny a póly se používají např. při zpracování signálu.

Interpolace

Často se stane, že daná funkce není definovaná formulkou, ale že ji dostaneme jako výsledek měření, takže máme k dispozici jen několik bodů.

Bohužel i v matematice platí zákon schválnosti a občas potřebujete znát funkční hodnotu i tam, kde jste neměřili. Například na obrázku vpravo máte změřenou hodnotu ve dvou bodech: f(3)=7 a f(4)=11. Vtom ale vrazí do vaší kanceláře šéf a dožaduje se hodnoty v bodě 3.6. Co teď?

Buďto můžete měření zopakovat a modlit se, že provozní náklady vaší aparatury nejsou moc vysoké, anebo zkusíte hodnotu v bodě 3.6 nějak odhadnout. Takovému procesu říkáme interpolace.

Její nejjednodušší varianta spočívá v tom, že naměřené hodnoty proložíme přímkou (viz obrázek vpravo) a z její rovnice pak spočítáme kterýkoliv mezilehlý bod (lineární interpolace).

Přímka má obecnou rovnici y = kx + q, a protože známe dva její body (3,7) a (4,12), lehce si sestavíme dvě rovnice pro dvě neznámé k a q (x-ové souřadnice bodů dosadíme za x a to samé pro y). Takto dostaneme:

7 = 3k + q
12 = 4k + q

Tyto rovnice vyřešíme a dostaneme rovnici interpolační přímky. V našem případě získáme odečtením k=5 a zpětným dosazením do první (nebo druhé) rovnice q = -8. Takže hledaná přímka (ta, co spojuje modré body na obrázku) má rovnici y = 5x - 8. Nás zajímá její hodnota v bodě x=3.6, takže ho dosadíme a získáme kýžený výsledek y = 10. Tuto hodnotu předhodíme šéfovi a máme od dalšího měření pokoj.

Kdo nemá soustavy rovnic rád, může si vypomoci selským rozumem (trojčlenkou). Mezi bodem 3 a 4 funkce vystoupá o 5 dílků (ze 7 na 12). My ale neprojedeme celou vzdálenost od 3 až do 4. Pojedeme jen do bodu 3.6, což je 60 % cesty. Pak je rozumné, aby funkce za tu dobu nastoupala jen o 60 % z těch 5 dílků. V bodě 3.6 tedy bude mít hodnotu 7 (to, s čím jsme začali) plus 60 % z 5 (to, co jsme cestou z bodu 3 nastoupali). A protože 60 % z 5 jsou 3, dostaneme stejný výsledek 7+3 = 10.

I v matematice samotné se někdy musí interpolovat. Klasickým příkladem je funkce faktoriál, známá například z kombinatoriky (značí se vykřičníkem, takže její hodnota v bodě x nebude fakt(x), ale x!). V originále je definovaná pouze pro přirozená čísla, a to tak že spočítáme součin všech čísel menších než x (až do jedničky, kde se zastavíme, protože další číslo je nula a ta by nám výsledky naší práce zhatila). Pár příkladů:

1! = 1
2! = 2 * 1 = 2
3! = 3 * 2 * 1 = 6
4! = 4 * 3 * 2 * 1 = 24
5! = 5 * 4 * 3 * 2 * 1 = 120 atd.

Nula faktoriál se definuje konvencí jako 0! = 1 (zde se dočtete proč).

Co se stane, pokud bude někdo chtít spočítat faktoriál, řekněme, v bodě 3.6? Původní definice tady evidentně nefunguje, protože se do té závěrečné jedničky „netrefíme“. Můžeme si ale vypomoci lineární interpolací. Jako základ si vezmeme výše spočítané hodnoty v přirozených číslech (to jsou ty zelené body, které jsem pro potřebu pozdějšího srovnání s gama funkcí posunul o jedničku). Graf takto vzniklé funkce (viz obrázek vlevo) má ovšem jednu vadu. Výsledná křivka není hladká, protože jak jsme přímky narychlo pospojovali, tak se v zelených bodech objevilo „drcnutí“ (tedy nespojitá změna směru).

To se dá ošetřit tak, že místo přímek proložíme zelené bodíky nějakým polynomem vyššího řádu (v praxi se často používají kubické polynomy). Ty mají volitelných koeficientů víc (přímka měla jen dva: k a q), takže je můžeme seštelovat tak, aby se směr (derivace) v těch zelených bodech vyrovnal. Tím dostaneme funkci (viz obrázek vpravo), která je hladká a pro přirozená čísla přesně souhlasí s faktoriálem (křivka opět prochází zelenými bodíky).

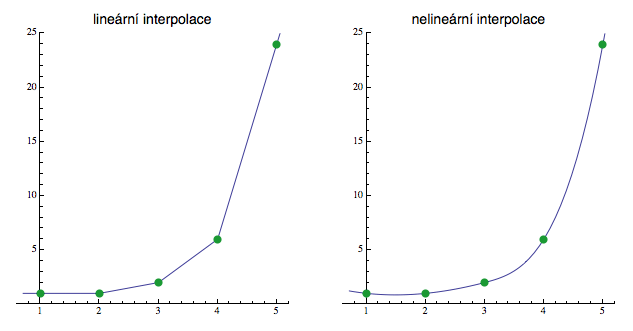
Když se na nelineární interpolaci dobře podíváte (např. mezi 3 a 4), uvidíte, že je tam trochu nepřirozeně vypouklá. To je proto, že faktoriál neroste polynomiálně (on roste daleko rychleji), takže snaha nahradit ho (byť jen lokálně) polynomem nedokáže přesně zachytit jeho skutečné vlastnosti.

Když si to rozmyslíte, tak křivka i při nelineární interpolaci využívá jen hodnot v několika sousedních bodech (ta lineární dokonce používala jen dva body). Jak se faktoriál chová o kus dál, je interpolační křivce úplně šuma fuk. A to je v podstatě nelogické. Křivka by měla reflektovat chování funkce faktoriál pro všechna čísla, ne jen ta sousední (je to jako byste při výpočtu průměrného platu v ČR spočítali jen průměr v Kotěhůlkách a na zbytek republiky se vykašlali).

A tak začali matematici koumat, jak definovat „interpolaci“ faktoriálu jinak.

Gama funkce - Γ(s)

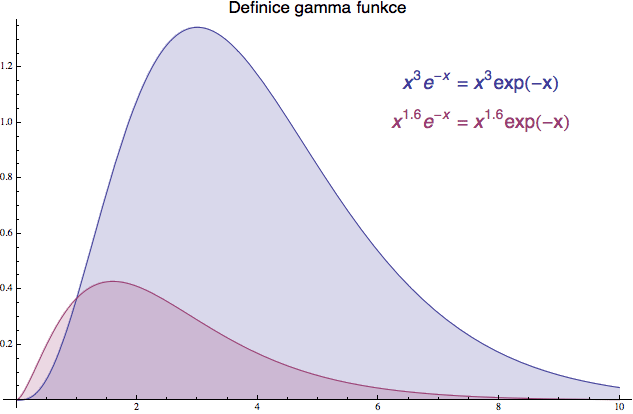
Představme si skupinu funkcí (dvě máte na obrázku níže), kterou dostanete tak, že nějakou mocninu x vynásobíte „obrácenou“ exponencielou - tedy exp(-x).

Obecně platí, že graf funkce f(-x) je oproti tomu původnímu „obrácený“ ve směru pravolevém (jako byste ho otočili kolem osy y). Tedy „pravá“ část funkce se ocitne vlevo a naopak.

Už v dávných dobách si mistři matematického řemesla povšimli, že když spočítáte plochu pod takovou funkcí odvozenou z n-té mocniny (a to od nuly poctivě až do nekonečna), tak dostanete přesně n!. To je ale náhodička, co?

Například na obrázku uvedená modrá funkce x³ exp(-x) má pod grafem plochu 6, což je 3! Pokud umíte integrovat, můžete si to sami spočítat metodou per partes. Funguje to pro všechna přirozená čísla. To, že je plocha konečná, přestože ji poctivě počítáte od nuly až do nekonečna, je způsobeno tím, že „obrácená“ exponenciela je pro velké hodnoty x tak blízko nule, že přírůstek plochy je pro ni prakticky zanedbatelný.

Někde v tomto místě zablikala v hlavě starých mistrů žárovka. Pokud můžeme spočítat faktoriál nějakého celého čísla tak, že příslušnou (celočíselnou) mocninu vynásobíme exponencielou a spočítáme plochu pod grafem, proč bychom ten samý postup nemohli použít pro jakoukoliv obecnou mocninu? Třeba pro exponent s=1.6: spočítáme plochu pod červenou funkcí dole a to, co nám vyjde, drze prohlásíme za 1.6!. A je to. Chcete spočítat a! pro nějaké desetinné číslo? Tak si prostě narýsujete funkci x^a*exp(-x) a pusťte se do integrování.

Tohle je mimochodem v matematice celkem běžný trik. Pokud chcete rozšířit nějaký pojem, vymyslíte definici, která je sice složitější, ale dá se aplikovat na více objektů. Ta definice faktoriálu pomocí plochy je opravdu drsná, ale umožňuje rozšíření na všechna desetinná čísla. Výsledkem je tzv. gama funkce.

gama(s) = plocha pod grafem funkce x^(s-1)*exp(-x) od nuly do nekonečna

(chcete-li vidět tu samou definici ve formě integrálu, mrkněte sem)

Takto definovaná funkce navíc splňuje (a to se musí samozřejmě spočítat) i známou faktoriálovou rekurzívní formulku: gama(s+1) = s*gama(s), takže se s ní dobře pracuje (viz níže).

To, že v definici funkce gama máme mocninu (s-1), znamená, že gama funkce je vzhledem k faktoriálu o jedničku posunutá. To je dílem věcí konvence a dílem historického vývoje (viz zde nebo zde). Platí tedy:

gama(n) = (n-1)! pro každé přirozené číslo n.

Jak taková funkce gama vypadá, vidíte na dalším obrázku.

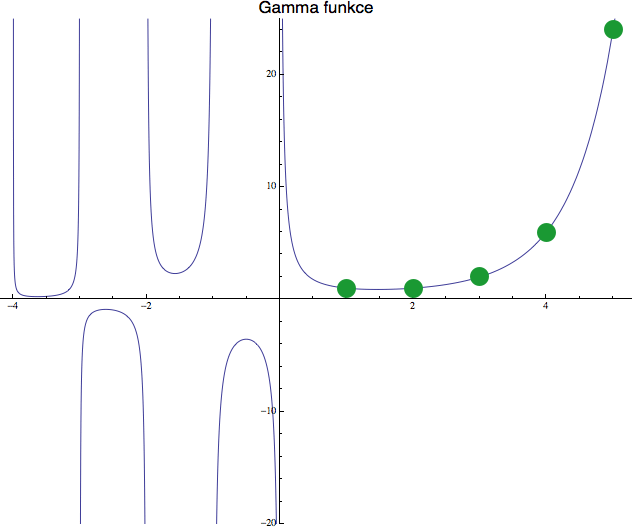
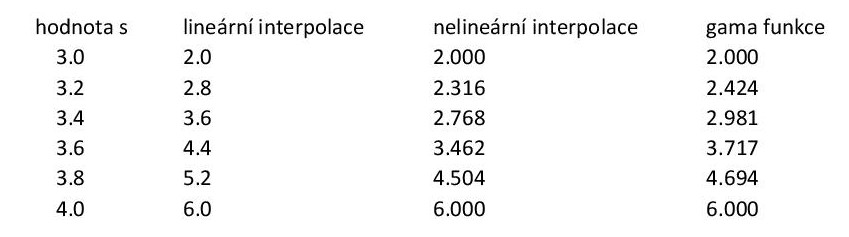
Všimněte si, že ta vypouklina mezi 3 a 4 už není tak hrozná. Tahle funkce je v jistém smyslu globální interpolací faktoriálu. Pokud chcete vidět, jak se předchozí interpolační křivky liší od gama funkce, tady je tabulka několika hodnot mezi 3 a 4. Pro s=3 dostaneme samozřejmě ve všech případech 2! a pro s=4 máme 3! (což je 6). Asi jste si všimli, že jako vstupní proměnnou používám s místo x. To je u vyšších funkcí běžné, aby se x netlouklo s integrační proměnnou (pokud pro definici používáte integrál - čili plochu).

Z grafu nahoře také vidíme, že funkce gama nemá žádné kořeny, ale zato má spoustu pólů. Ty sedí v nule a v záporných celých číslech (tedy s=0,-1,-2,-3...). „Obrácená“ funkce gama(-x) bude mít naopak póly v nezáporných celých číslech (tedy s = 0,1,2...). Když je tedy obě vynásobíme, gama(s) * gama(-s), dostaneme funkci s póly ve všech celých číslech (v nule dokonce dvakrát). (To je proto, že pokud je nějaká funkce součinem dvou jiných funkcí, tak její kořeny získáme sjednocením kořenů obou dílčích komponent. A pro póly to platí jakbysmet.

Minule jsme viděli, že funkce sin(x) má kořeny v celočíselných násobcích π (3,14..). To znamená, že funkce sin(πx) bude mít kořeny v celých číslech a její převrácená hodnota 1/sin(πx) bude mít v celých číslech póly.

Takže až na tu dvojnásobnou nulu má funkce 1/sin(πx) stejné póly jako součin těch dvou gama funkcí. To přivedlo některé matematiky k otázce, zda tyto funkce náhodou nejsou stejné. Pomalu se v tom začali vrtat a brzy zjistili, že jsou skutečně prakticky identické (aby se zbavili toho přebytečného pólu v nule, jednu gama funkci posunuli o jedničku). Výsledek jejich úsilí je slavná Eulerova reflexní formulka:

gama(s)*gama(1-s) = π / sin(πs)

Dobře si ji prohlédněte. To je ten typ výsledku, o kterém jsem mluvil na začátku. Spojuje dva zcela rozdílné světy. Na levé straně máme součin dvou interpolovaných faktoriálů - tedy něco, co úzce souvisí s kombinatorikou. Napravo je zase sinus, tedy funkce pocházející z geometrie trojúhelníků. A přesto jsou v Eulerově formulce tyto dva světy propojeny neviditelnou pupeční šňůrou. Je to jako byste v tkanivu vesmíru narazili na „červí díru“ (wormhole). A tohle je jeden z těch malých zázraků, po kterých matematici pasou.

Vzoreček ale neslouží jen k filosofickému hloubání o mazanosti pánaboha. Můžeme ho použít například k výpočtu hodnoty gama funkce v konkrétních bodech. Když si do něj dosadíte s=1/2, dostanete:

gama(1/2)² = π (protože sin(π/2) = 1)

a to znamená, že gama(1/2) = sqrt(π) = 1.77245.

No dobře, to byl trochu fígl. Kdo si chce gama funkci v jedné polovině spočítat natvrdo, může se mrknout sem.

A k čemu je taková funkce dobrá? Gama funkce se používá jednak ve fyzice a statistice, ale má svůj praktický význam i v čisté matematice - můžete si s její pomocí spočítat např. objem koule o poloměru R v n-rozměrném prostoru:

V(R,n) = π^(n/2) * R^n / gama(1+n/2)

Podívejme se nejdřív, zda ten vzoreček vůbec souhlasí s tím, co známe ze školy. Pro n=2 (tedy kruhový obsah) dostaneme

V(R,2) = π * R^2 / gama(2)

a protože gama(2) je 1! = 1, dostaneme přesně to, co očekáváme.

A teď objem pro třírozměrnou kouli (n=3).

V(R,3) = π^(3/2) * R^3 / gama(5/2)

Nejdřív se budeme muset vypořádat s gamou pomocí výše zmíněné rekurzívní formulky gama(s+1) = s*gama(s). A protože gama(1/2) už známe, dostaneme

gama(5/2) = (3/2) * gama(3/2) = (3/2) * (1/2) * gama(1/2) = (3/4) * sqrt(π)

No a teď to dáme všechno dohromady

V(R,3) = π^(3/2)*R³ / (3/4)*sqrt(π) = (4/3) * π * R³

Tohle ale známe ze školy. Proto si na závěr dáme 4rozměrnou kouli.

V(R,4) = π² * R^4 / gama(3) = π² * R^4 / 2

A za domácí úkol si můžete spočítat, že (hyper)objem 5-rozměrné koule bude

V(R,5) = π^(5/2)*R^5 / gama(7/2) = (8/15) * π² * R^5

Zeta funkce - ζ(s)

Ještě na jednu vyšší funkci se podíváme, hlavně proto, že už jsme ji v minulosti trochu nakousli. I tato je označená řeckým písmenkem a říká se jí (Riemannova) funkce zeta. Její definice je vcelku jednoduchá. Pro danou hodnotu s vám tato funkce na výstupu vyhodí součet nekonečné řady převrácených hodnot přirozených čísel umocněných na exponent s. Následující obrázek ukazuje hodnotu zeta funkce pro exponenty s=2, 3 a 4 (vlevo jsou vstupní hodnoty, vpravo výstupní).

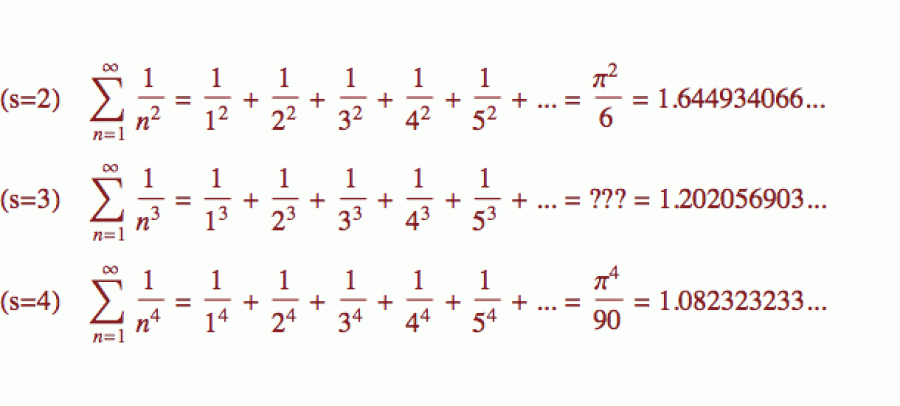
Samozřejmě na celých číslech není z pohledu umocňování nic speciálního a Riemannova zeta funkce je definovaná pro každé reálné s, pro které má příslušná řada konečný součet.

Vzhledem k tomu, že pro velké hodnoty s se členy definiční řady poměrně rychle zmenšují, můžete si solidní aproximaci zeta funkce spočítat doslova na koleně. Např. zeta(5) bude součet převrácených hodnot: 1/1, 1/2, 1/3, 1/4... umocněných na pátou:

zeta(5) = 1+1/32+1/243+1/1024+1/3125+...

Těch pár členů napravo vám dá 1.03666, což je solidní aproximace celého nekonečného součtu, který je roven zeta(5) = 1.03695.

Pokud vaše kalkulačka umí počítat i s neceločíselnými mocninami, můžete si zkusit přibližně spočítat zeta(5.3) = 1.02933 (čím více členů sečtete, tím bude váš výsledek přesnější).

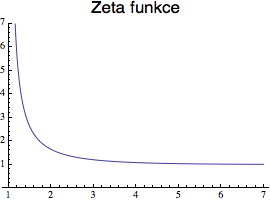
Napravo vidíte graf zeta funkce pro s>1 (to jsou hodnoty s, pro které má řada konečný součet). Všimněte si, že v bodě s=1 má tato funkce pól.

Význam zeta funkce spočívá v tom, že nám poskytuje jakýsi teleskop, kterým můžeme nahlížet do tajemného světa prvočísel. Toto uvidíme nejlépe, pokud si na definiční řadu trochu posvítíme (nejprve ve zjednodušené podobě - viz první řádek obrázku dole). Na levé straně máme součet reciprokých hodnot přirozených čísel. Na pravé pak nekonečný součin závorek, z nichž každá obsahuje výčet reciprokých mocnin jednoho konkrétního prvočísla s tím, že každé prvočíslo má v součinu svou závorku - 2, 3, 5, 7, 11 atd. (proto jsou tři tečky nejen v každé závorce, ale také za poslední závorkou, za kterou následují další a další). Rozmyslete si, že to, co v každé závorce vidíte, je de facto geometrická řada.

Abychom lépe nahlédli do první rovnice, uvědomme si, že při roznásobování závorek na pravé straně (podle distributivního zákona) vlastně uvažujeme součiny, kdy z každé závorky vybereme právě jeden člen. Při tom jsme buď vybrali nekonečně mnoho členů, které nejsou jedničkou (a jejich součin pak bude nula), a nebo máme těch nejedničkových členů pouze konečně mnoho a pak nám každý takový součin dá jedno číslo na levé straně (podle jednoznačnosti rozkladu na prvočinitele).

Např. 45 = 3² 5. To znamená, že člen odpovídající nalevo výrazu 1/45 dostaneme napravo tak, že z první závorky vybereme 1, z druhé 1/3², ze třetí 1/5 a ze všech dalších už jen 1. A takhle si ze stavebnice na pravé straně „sestavíte“ každý člen na levé straně.

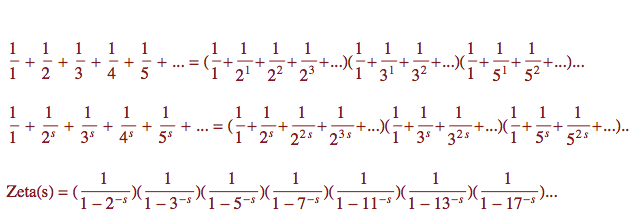
Na druhém řádku máte přesně to samé, jen je tam každý člen ve své s-té mocnině. Rovnost se ukáže úplně stejnou metodou. A na třetím řádku už je jen souhrn. Nalevo je dle definice Riemannova funkce zeta a napravo dostaneme v každé závorce součet geometrické řady a ten je tam naznačen (nezapomeňte, že záporné mocniny jsou převrácené kladné mocniny - viz sekce Jauvajs zde). Tomuto zápisu se říká vyjádření zeta funkce pomocí Eulerových součinů.

Nalevo máme tedy naši krásnou funkci (kterou můžeme derivovat, integrovat a všemožně pitvat) a napravo nekonečný součin přes všechna prvočísla. Mimochodem, určitě jste si všimli, že zatímco graf funkce je krásně spojitý (ba hladký), prvočísla sama o sobě jsou notoricky nepravidelná. A právě ve spojení těchto dvou protikladů (spojitost a pravidelnost funkčního grafu versus rozháranost prvočísel) tkví význam a přitažlivost funkce zeta. A nejen pro matematiky.

V klasické mechanice byla Teorie čísel považována za trochu ezoterickou disciplínu, nemající nic do činění se skutečnými zákony tohoto světa. Jaký je taky prvočíselný rozklad reálného čísla (např. π)? To nedává smysl. Jenže v okamžiku, kdy fyzikové objevili kvantovou mechaniku a zjistili, že náš svět není až tak spojitý, jak se původně domnívali, začali se o vše, co souvisí s celými čísly, intenzivně zajímat. A zjistili například, že rozdělení energetických hladin v některých kvantových systémech podezřele připomíná rozdělení kořenů Riemannovy funkce zeta. Možná i proto je na nalezení všech kořenů této funkce vypsána odměna milion dolarů (dokonce je ani nemusíte najít, stačí jenom, když ukážete, že leží na určité přímce - což je tvrzení, kterému se říká Riemannova hypotéza).

(poznámka po uzávěrce: v září 2018 přednesl známý britsko-libanonský matematik a nositel Fieldsovy medaile, Michael Atiyah, svůj důkaz Riemannovy hypotézy vycházející z prací Johna von Neumanna a Friedricha Hirzebrucha - tento přístup momentálně zkoumají odborníci)

Jako ilustraci zvýšeného zájmu fyziků o teorii čísel (a speciálně o Riemannovu funkci zeta) jsem pro vás na závěr vybral několik zajímavých odkazů:

Quantum Physicists Attack Math's $1,000,000 Question
From Prime Numbers to Nuclear Physics and Beyond
Riemann Zeta function and connection to Quantum Mechanics
How (Not) to Sum Natural Numbers (Zeta Function Regularization)
Hilbert-Pólya conjecture

A ještě pár techničtějších článků ve formátu PDF:

The physics of the Riemann Zeta function
The Riemann Zeta function and the connection to Hamiltonians in Physics
Quantum chaos, the random matrix theory and the Riemann zeta function
Links between string theory and the Riemann Zeta function

Při pohledu na graf zeta funkce si možná říkáte, jak může mít tato funkce nějaké kořeny, když je všude kladná... A prozatím máte pravdu. Tak jako jsme faktoriál pomocí gama funkce rozšířili z přirozených čísel na reálná čísla, i zeta funkci budeme muset trochu rozšířit, aby nám něco zajímavého ukázala. Tím se dostaneme do komplexní roviny, a proto si příště zopakujeme komplexní čísla.

Článek je redakčně upravenou verzí blogového příspěvku na serveru iDNES.cz. Publikováno s laskavým svolením autora.

Další díly a původní texty jsou dostupné na blogu Jana Řeháčka.

Autor: Jan Řeháček