Vektorové prostory jsou pro vybudování pojmu dimenze optimálním prostředím, ale mají jednu nevýhodu. Zdaleka ne vše kolem nás je „rovné“. Aby mohli matematici propašovat dimenzi do zakřivených prostranství, vymysleli si „varietu“.
Minule jsme si řekli, že v případě vektorového prostoru, tedy „prostředí“, kde se dá sčítat a násobit skalárem, se dimenze definuje jako maximální počet nezávislých směrů (vektorů), anebo minimální počet vektorů, ze kterých se vektorový prostor dá zrekonstruovat (pomocí lineárních kombinací). Lidově řečeno, dimenze nám říká, kolika různými nezávislými směry se v daném „prostředí“ můžeme vydat anebo kolik souřadnic potřebujeme k udání své polohy. Ve 3D, kde trávíme většinu svého života, tedy budeme potřebovat tři a je jedno, zda si vybereme kartézské (x,y,z), sférické (r,fi,psi), cylindrické (r,fi,z) nebo jakékoliv jiné.
Jenže občas to prostředí není vektorový prostor. Nežijeme v eukleidovské rovině (tedy vektorovém prostoru R2), ale na zakřiveném kousku sféry (ponořeném do R3). Přesto cítíme, že náš svět je v zásadě dvourozměrný: při pohybu můžeme kombinovat dva základní směry, a to dopředu-dozadu, anebo doleva-doprava (tedy pokud nejsme zrovna ve Špindlu). Dokonce ani náš vesmír není úplně „rovný“ - jak vyplynulo z Einsteinova zkoumání gravitace v obecné teorii relativity - takže dívat se na něj jako na R3 taky není úplně košer (a ani Minkowského časoprostor to nevytrhne).
Pokud se mravenec šine po prádelní šňůře, tak nějak tušíme, že jeho prostředí bude asi jednorozměrné: má na vybranou pouze jeden směr - dopředu-dozadu - a jeho polohu lze označit jedním číslem (souřadnicí), např. vzdáleností od nejbližšího „sloupku“. Jenže přes vektorové prostory to ani zde hnát nemůžeme, protože šňůra, respektive její tvar není přímka. A není to mimochodem ani parabola, jak by se leckdo mohl domnívat. Nedostatečně vyšponované šňůry, kabely či dráty mají tvar tzv. řetězovky (anglicky catenary), což z pohledu matematiky není nic jiného než graf hyperbolického kosinu (no vidíte, bez těch hyperbolických funkcí na kalkulačce byste si ani neusušili prádlo).
Aby mohla matematika rozšířit pojem dimenze i do těchto hájemství, musela definovat něco, co lokálně vypadá jako ohnutá kopie vektorového (eukleidovského) prostoru. A tak spatřila světlo světa tajuplná varieta) (anglicky manifold), která se stala jedním z nejdůležitějších nástrojů moderní matematiky a představuje ucelený a univerzální rámec pro studium zakřivených prostorů. Nuže, tady je to, varieto!
Jak ohnout vektorový prostor
Pojem varieta je založen na fenoménu, který všichni dobře známe. Často se nalézáme v prostředí, které sice není eukleidovským prostorem, ale svým chováním se od něho příliš neodlišuje. Nejsilněji to na nás dolehne při výletu do Polabí. Jedeme z Nymburka do Kolína a ubíhající krajina nám vsugerovává pocit, že se pohybujeme v rovině xy, tedy ve dvoudimenzionálním médiu, a že bychom tady u Poděbrad mohli krásně studovat přímky, kružnice, trojúhelníky a všechnu tu eukleidovskou drobotinu. Jenže zdání klame. Ve skutečnosti jsme na povrchu sféry, což bychom si mohli lehce ověřit tak, že bychom jeli (nebo raději letěli) stále stejným směrem a za nějaký čas bychom se vrátili do výchozího místa. Něco takového by se nám v eukleidovské rovině nestalo.
Varieta je tedy něco, co lokálně vypadá jako eukleidovský prostor, a dimenze tohoto prostoru pak definuje dimenzi variety. Proto je prádelní šňůra jednorozměrná, zatímco Polabí je dvourozměrné. A jak se ta varieta chová globálně, do toho nám nic není. Globálně si může dělat ledasjaké skopičiny. Například zeměkoule by někde v oblasti Antarktidy klidně mohla být nabodnutá na kůl trčící z nekonečné bažiny a žádným geometrickým měřením v Evropě bychom to nikdy nezjistili. Na obrázku jednu takovou varietu vidíme. Z našeho pohledu je jasně zakřivená, ale kdybyste byli malým mravencem na ní, lehce byste propadli dojmu, že je to prachobyčejná rovina.
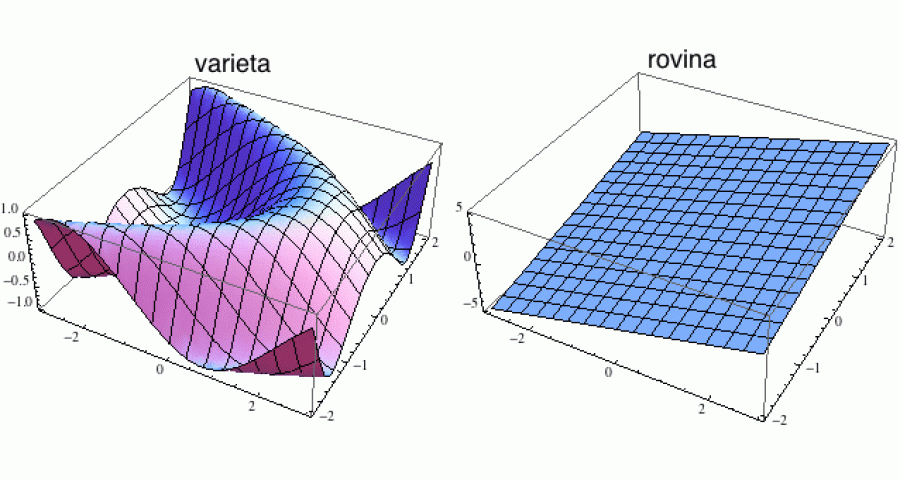
Dokonce byste si na tu varietu mohli křídou nakreslit dvojici souřadnic (tak jak je to naznačeno vlevo) a to by jen zesílilo váš dojem, že žijete v rovině. Přímky monotónně ubíhají kupředu, trojúhelníky mají tři strany, kružnice jsou plus minus kulaté a stěrače bezchybně stírají. Prostě pohoda. Pouze kdybychom měli extrémně přesné měřicí přístroje, tak bychom zjistili, že s naší geometrií není něco v pořádku, ale to by byla trochu jiná pohádka (na to se podíváme jindy). Prozatím se spokojíme se zjištěním, že lokálně (tedy pokud neodbíháme příliš daleko) se všechno zdá být v eukleidovském richtigu a to nám k rozšíření pojmu dimenze postačí. Geometrii vzal čert.
To, že se něco lokálně „podobá“ eukleidovskému prostoru, je ale trochu vágní tvrzení. To by se taky někdo mohl v půl třetí vracet z hospody v Kersku a vyřvávat na lesy, že všechno okolo vypadá jako šestirozměrný prostor, a hnedle bychom měli 6D Polabí. Musíme do toho „podobání“ zavést trochu objektivity. Matematika to řeší velmi prakticky: autoatlasem.
Autoatlas je vlastně série map (zobrazení) mezi povrchem země a kouskem 2D eukleidovského prostoru (stránka mapy). A to zobrazení je vzájemně jednoznačné. Tedy nestane se, že by se dva body na Zemi zobrazily do stejného místa na mapě a naopak, dva různé body na mapě vždy odpovídají dvěma různým místům na Zemi.
Všimněte si také, že autoatlas je lokální - nečiní si žádné nároky, že by celou Zemi zobrazil na jedné stránce - to by taky byl dost problém. Každá stránka atlasu pokrývá (zobrazuje) pouze relativně malý kousíček. A na varietách to funguje obdobně.
Nejprve ji úplně pokryjeme překrývajícími se „záplatami“ a pak jednu každou z nich zobrazíme (pomocí mapy) do nějakého eukleidovského prostoru, z něhož odvodíme dimenzi variety. Ta zobrazení jsou vlastně určitým typem funkce. Vstupní hodnota je bod na Zemi, výstupní pak bod na mapě. A pro inverzní zobrazení naopak.
A teď trochu techničtěji (tuto podsekci můžete vypustit). Za prvé. Ty „záplaty“ se nezobrazují jen tak na jakékoliv „kusy“ eukleidovského prostoru, ale na tzv. otevřené množiny (zobecnění otevřených intervalů z číselné osy), které jsou charakterizované tím, že s každým bodem obsahují i nějaké jeho malé „okolíčko“. Tato vlastnost nám umožňuje přenést vlastnosti vektorového prostoru na varietu, protože otevřené množiny mají plnou dimenzi (tj. uvnitř nich se můžeme pohybovat přesně tolika nezávislými směry jako v celém prostoru).
Kdybychom od té „otevřenosti“ upustili, tak by se s dimenzí dalo švindlovat. Někdo by mohl říct: „Hele, tenhle provázek vypadá lokálně jako úsečka, což je kus eukleidovské roviny, a tudíž je ten provázek dvourozměrný.“ Jo, houbeles. „Kus“ roviny to sice je, ale není to otevřená množina (a mimochodem, i ty „záplaty“ musejí být otevřené množiny na varietě).
Pro ilustraci otevřenosti se podívejme na další obrázek. Červená úsečka (bez krajních bodů) je otevřenou podmnožinou modré přímky (vlevo), ale není otevřenou podmnožinou modré roviny (vpravo). Vlevo je vidět, že pro každý bod p najdeme malé (zelené) okolíčko, které bude součástí červené úsečky. Vpravo se to nepodaří. Tam nám sebemenší okolíčko bodu p „vyteče“ mimo červenou úsečku.
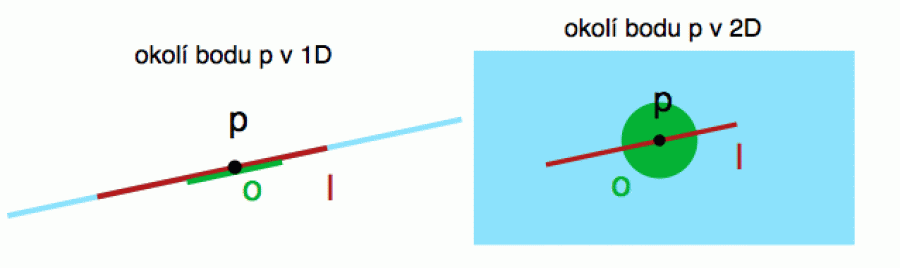
Proto má ta červená úsečka vlevo plnou dimenzi přímky (je to její otevřená podmnožina), zatímco vpravo ta samá úsečka plnou dimenzi roviny nemá (není to otevřená podmnožina roviny).
Za druhé. Zobrazení, které „mapuje“ varietu na otevřený kousek eukleidovského prostoru, musí být rozumné. Nejenže musí být vzájemně jednoznačné (jinak by nemělo smysl), ale nesmí tu varietu „roztrhat“, přesněji musí být spojité oběma směry. Tedy jak zobrazení z variety do mapy, tak i jeho inverzní z mapy do variety. Dva blízké body na varietě se i na mapě zobrazí blízko a naopak: dva blízké body na mapě odpovídají místům, které jsou si blízko i na varietě. Takovým zobrazením říkáme homeomorfismy.
Pro zeměkouli existuje celá řada projekcí (např. známá Mercatorova projekce), které dokáží zobrazit velkou část jejího povrchu do roviny. Matematika nevyžaduje, aby se „většina“ variety dala zobrazit najednou, a může si tedy při projekci dovolit určitou „vůli“. Požadavek spojitosti oběma směry ukazuje, kam až s tou „vůlí“ můžeme zajít (dobře vycvičený šťoural by se mohl podivit, proč se musí požadovat i spojitost inverze, když o reálných funkcích je známo, že pokud jsou spojité a prosté, tak mají spojitou inverzi; jádro pudla spočívá v tom, že zde máme zobrazení do nějaké variety a tam je ta spojitost inverze komplikovanější).
Kdo někdy listoval autoatlasem, určitě si všiml, že jednotlivé mapy mají určitý „přesah“ (tj. co je na str. 24 v levém okraji musí odpovídat tomu, co je v pravém okraji na str. 25) a ten přesah musí zobrazovat realitu kompatibilním způsobem (bylo by skandální, kdyby na str. 24 byla vzájemná poloha měst jiná než na str. 25).
I jednotlivé záplaty naší variety mají určitý „přesah“ (což vyplývá z toho, že jsou to otevřené množiny), a když ten společný přesah zobrazíme pomocí dvou různých map, musíme (stejně jako kartografové) dostat kompatibilní obrázek.
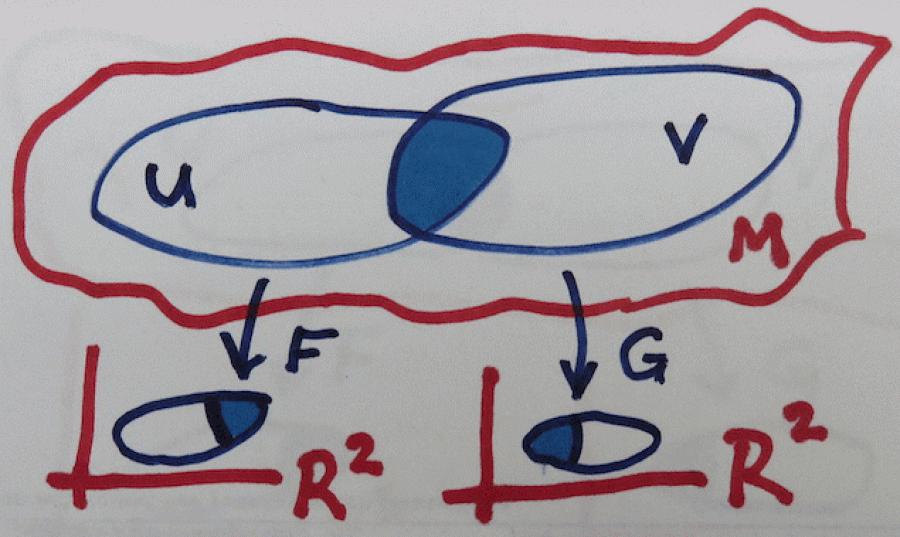
Na této ilustraci vidíte dvě mapy, které zobrazují dvě „záplaty“ (U a V) variety M do R2. Společná modrá část obou záplat se tedy zobrazí jak do levé mapy (zobrazením F), tak do pravé (zobrazením G). Když složíte inverzní zobrazení k F (které vede z levé mapy do variety) se zobrazením G (které vede z variety do pravé mapy), tak dostanete zobrazení z modrého území levé mapy do modrého území pravé mapy (říká se mu přechodová funkce a funguje z R2 do R2, takže se dá poměrně snadno studovat) a jeho vlastnosti určují míru kompatibility mezi jednotlivými mapami.
Zjednodušeně řečeno, pokud jsou tyto přechodové funkce jen spojité (homeomorfismy), mluvíme o topologické varietě, pokud jsou navíc i hladké (difeomorfismy), mluvíme o diferencovatelné varietě. Na ní se potom dá vybudovat infrastruktura umožňující zavedení diferenciálního počtu (což je záhodno, pokud chcete na varietě studovat nějaké procesy popsané diferenciálními rovnicemi - např. vedení tepla).
(Ještě lépe vycvičený šťoural by teď mohl říct: „No dobře, tak máme nějakou zohýbanou varietu, pokryjeme ji otevřenými záplatami a každou záplatu zobrazíme do otevřené podmnožiny nějakého eukleidovského prostoru. Ale co když ta levá mapa a pravá mapa vedou do prostorů s jinou dimenzí? Jak pak můžeme definovat jednu dimenzi platnou pro celou varietu?“ Půvab je v tom, že k tomuto politováníhodnému nedopatření nemůže dojít ani jednou za deset let. Přechodové zobrazení by pak reprezentovalo homeomorfismus mezi prostory různé dimenze a to není možné - např. rovina se nedá homeomorfně zobrazit do prostoru. Důkaz je ale poměrně obtížný.)
Aby ale nevznikl dojem, že všechno, co se nějak křiví, je varieta, podívejme se na číslovku „8“. Zatímco oba obloučky vypadají lokálně jako kousek přímky, ten centrální bod (zkřížení) nevypadá ani jako přímka, ani jako rovina, a nedá se do nich homeomorfně zobrazit (podrobnosti zde). Abychom z osmičky udělali varietu, museli bychom se přesunout do 3D a jeden oblouček v tom zkřížení „přizdvihnout“ (aby se z osmičky stala taková ta klasická autodráha s mimoúrovňovým křížením centrální části). Pak by se celá mimoúrovňová osmička dala homeomorfně zobrazit na několik otevřených úseček a stala by se z ní 1D varieta.
Zatím jsme se na varietu dívali víceméně lokálně. Ale co globální struktura? Následující obrázek ukazuje balón (sféru) a pneumatiku (torus).
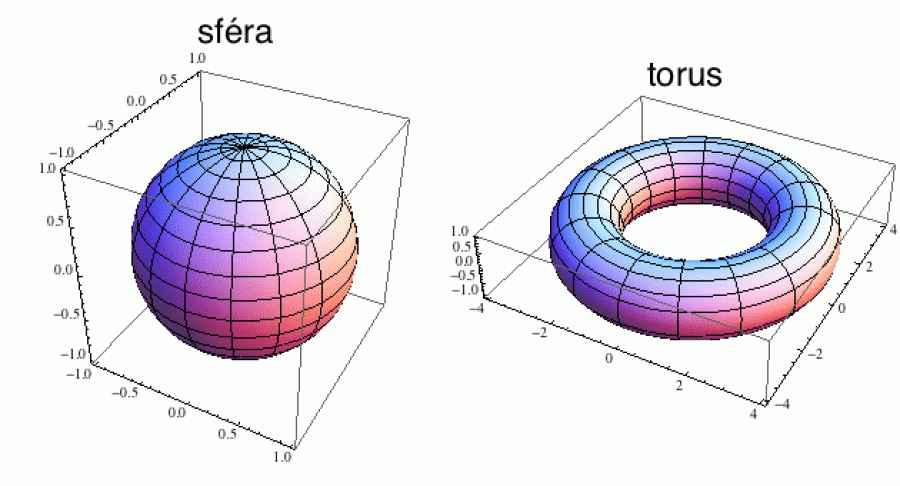
Když si představíte, že jste malý mravenec, obě variety vám budou lokálně připomínat eukleidovskou rovinu. Jsou to tedy 2D variety. Ale globálně vypadají zcela jinak a mají taky různé topologické vlastnosti, které se nedají jen tak lehce odvodit z lokální perspektivy. Když například sféru rozstřihnete podél vnějšího obvodu (rovníku), rozpadne se na dvě části; torus se nerozpadne, jen se z něj stane takový zdeformovaný válec.
Studium globálních vlastností variet je mnohem komplikovanější a historicky vzato začíná u Eulerova slavného postřehu, že pro konvexní mnohostěny platí rovnice:
V - H + S = 2 (tzv. Eulerova věta)
kde V je počet vrcholů, H počet hran a S počet stěn.
Výraz nalevo tedy představuje určitý invariant, který je všem mnohostěnům společný. To vedlo matematiky obecně ke studiu dalších invariantů (v obecnějším kontextu variet) a výsledkem byla tzv. Bettiho čísla, která zhruba řečeno udávají počet n-rozměrných „děr“ v dané varietě.
To už jsme v druhé polovině 19. století a z usilovného bádání mezitím vyplynulo, že pro klasifikaci variet bude nutné odhlédnout od jejich spojitých deformací. Jinak bychom si mohli sednout na nafouknutý plážový balón a tvrdit, že výsledná „šiška“ je zbrusu nový typ variety.
Spojité deformace se obvykle definují pomocí homotopií, ale pro jednoduchost si je budeme i nadále představovat jako homeomorfismy. Abyste si udělali představu, jak moc takový homeomorfismus dokáže deformovat, můžete se mrknout na tuto klasickou animaci, která ukazuje spojitou proměnu hrníčku na torus. Časem se ukázalo, že pokud odhlédneme od deformací, tak kruciálním kritériem pro kategorizaci 2D variet je právě počet „děr“ (všechno ostatní se dá zakamuflovat „hnětením“), což mimochodem znamená, že o jejich skutečně fundamentálních vlastnostech rozhodují myši. Podrobné studium děr ve varietách vedlo k zavedení důležitého pojmu genus), který se stal klíčovou ingrediencí pro klasifikaci uzavřených povrchů.
Dvacáté století pak přineslo bouřlivý rozvoj algebraických metod pro analýzu globálních vlastností variet a většina z nich je více či méně spojena se studiem homologií a kohomologií, které představují komplikovanější typy invariantů asociovaných s danou varietou (to už je ale velmi náročná disciplína, do které by se člověk neměl pouštět bez solidního úrazového pojištění). V nejjednodušší variantě se hledají triangulací - varieta se pokryje sítí trojúhelníčků (či obecněji simplexů) a z vlastností té sítě se pak dovozují globální vlastnosti variety.
Většina variet, které jsme zatím uvažovali, byly 1D nebo 2D. Jakmile se dostaneme ke 3D varietám, vzduch podstatně zhoustne. 3D varieta je něco, co lokálně vypadá jako 3D eukleidovský prostor, ale může to být v nějaké vyšší dimenzi zakřivené. S takovou představou obtížně zápasí i ti nejlepší matematici, jak ukazuje příběh Poincarého hypotézy, která byla dokázaná teprve po sto letech (problém vyřešil ruský matematik Grigori Perelman v roce 2006). Domněnka tvrdí, že každá 3D varieta, která je uzavřená a jednoduše souvislá, je homeomorfní 3D sféra. To znamená, že pokud něco lokálně vypadá jako 3D prostor, nemá to hranici (uzavřenost) a nejsou v tom díry skrz naskrz (jednoduchá souvislost), tak je to víceméně zdeformovaná 3D sféra (stejně jako ten hrníček výše byl víceméně zdeformovaný torus).
Ta „jednoduchá souvislost“ také znamená, že každá uzavřená křivka na varietě se dá zdeformovat na bod. Pro sféru to platí (třeba padesátý poledník lehce zdeformujete na severní pól postupným scvrkáváním, aniž byste tu sféru opustili), zatímco pro torus ne (např. obvodovou kružnici na bod nikdy nezdeformujete). Proto torus není jednoduše souvislý. Je v něm díra.
Aby nedošlo k mýlce, závěrem ještě poznámku k terminologii ohledně sfér. Kružnice je 1D sféra (někdy se říká pouze 1-sféra), přestože „žije“ v 2D rovině. Ale lokálně se podobá přímce, a je proto jednorozměrná. Obdobně povrch zeměkoule je 2D sféra (neboli 2-sféra), přestože „žije“ v 3D prostoru. Jako varieta je ale dvourozměrná (což ví každý, kdo někdy projížděl Polabím). Ta 2D sféra je de facto hranicí 3D koule (stejně jako je 1D kružnice hranicí 2D kruhu).
Jestliže tedy Poincaré mluví o 3D sféře (3-sféře), má na mysli povrch 4D koule (tedy množinu bodů, které mají ve 4D prostoru stejnou vzdálenost od počátku) a to je pro naši imaginaci zatraceně těžký oříšek (více o čtvrté dimenzi příště).
Tohle je pro nematematiky trochu matoucí, protože člověk je zvyklý uvažovat v intencích prostoru, ve kterém daný objekt „žije“. Naše zeměkoule by tedy měla být 3D sféra, protože přece žije v 3D prostoru. Jenže takový přístup by nás brzy dovedl ke sporu. Vlnící se niť (což je matematicky vzato 1D varieta) by mohla žít jak v 2D prostoru (pokud ji upustíme na stůl), tak v 3D prostoru (pokud ji vystrčíme z okna a necháme vlát), takže by pak nebylo jasné, zda je taková niť 2D nebo 3D. Proto se smiřme s tím, že žijeme na 2-sféře, a nikoliv na 3-sféře.
Jak ohnout vektory
Pokrytí variety autoatlasem není jediný způsob, jak z ní vymámit informaci o dimenzi. Ta se dá odvodit i z tečného prostoru (který je v podstatě zobecněním pojmu „tečna ke kružnici“).
Nejprve si připomeneme (obrázek vlevo) definici tečného vektoru k nějaké křivce. Představme si bod, který se po křivce pohybuje tak, že v čase t má polohu x(t). Tečný vektor u pak reprezentuje okamžitou rychlost (včetně směru) tohoto bodu. Křivka vlastně reprezentuje jakési koleje, po kterých se bod pohybuje, a tečný vektor ukazuje - pro každý čas t - kam by ten pohybující se bod odletěl, kdybychom koleje najednou odstranili.
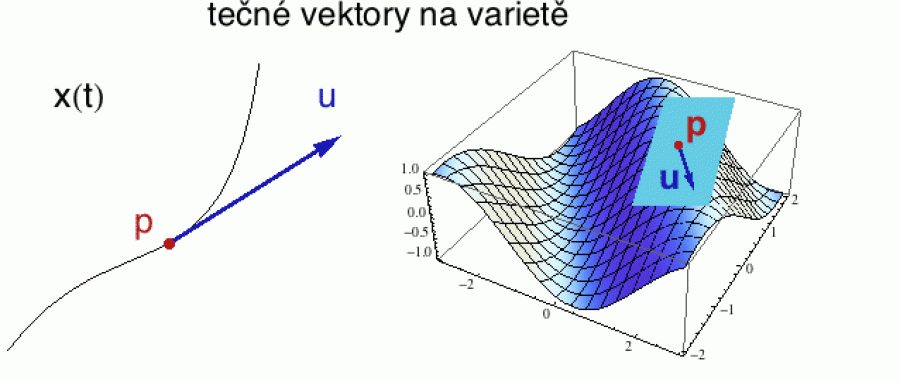
V každém bodě p naší variety (obrázek vpravo) můžeme uvažovat všechny možné křivky, které tím bodem procházejí. Každá taková křivka má v bodě p tečný vektor a kolekce všech takových vektorů tvoří tečný prostor v tomto bodě. Tečný prostor je tedy tvořen všemi možnými směry, které varieta M v daném bodě nabízí, a obvykle se značí TpM (kde p je subscript). Je to vektorový prostor, který můžeme přiřadit každému bodu variety, a v těch jednodušších případech si ho můžeme představit jako nejlepší lineární aproximaci. Jeho dimenze je stejná jako dimenze variety (odvozená z autoatlasu) a jeho počátek je v bodě p. Tečný prostor se samozřejmě s bodem p mění. Stejně jako tečna ke kružnici (pro sféru je to vidět třeba tady).
Na začátku této minisérie jsme si řekli, že vektory jsou v podstatě body, které si vezou svůj vlastní počátek s sebou (na úpatí každé šipečky), aby se daly snadněji sčítat. V eukleidovském prostoru je každý vektor „zaparkovaný“ v počátku a podle potřeby jím můžeme šoupnout tam, kam potřebujeme. Pokud chceme zdůraznit, že nějaké vektory už jsou „zaparkované“ v nějakém bodě p, mluvíme o tzv. vázaných vektorech.
Na varietách jsou de facto všechny vektory vázané, protože jsou „zaparkované“ v tečných prostorech a ty náleží jednotlivým bodům variety. To znamená, že na varietách jsou body a vektory pohodlně odseparované a každý vidí, co je bod (variety) a co je vektor (tečného prostoru). Zaplatili jsme za to ovšem nemalou cenu.
Když ve vektorovém prostoru potřebujete vektor šoupnout, tak ho prostě rovnoběžně přesunete na nové parkoviště. Na varietách je to podstatně komplikovanější. Když si vezmete vektor z tečného prostoru v bodě p a budete ho chtít šoupnut do tečného prostoru v bodě q, tak zjistíte, že není úplně jasné, který z vektorů v bodě q by mu měl vlastně odpovídat (více o tomto netriviálním problému najdete zde). Přirozeným propojením tečných vektorových prostorů podél zakřivených variet se zabývá diferenciální geometrie, která je denním chlebíčkem například pro fyziky zabývající se obecnou teorií relativity (v ní se zakřivení prostoru vztahuje k rozložení hmoty a energie v něm).
Samozřejmě byste mohli popadnout palici a zohýbaný vektorový prostor (tj. varietu) zase vyklepat, aby byl rovný. Pak by se všechny ty tečné prostory staly jen posunutými verzemi jednoho a toho samého a vy byste opět mohli svými vektory šoupat dle libosti, protože by se vše odehrávalo v tom samém „médiu“. Díky tomu můžeme v „rovném“ prostoru definovat vektory jako rozdíly bodů (na varietě by nám ty rozdíly trčely z „média“ ven).
To, že ve vektorovém prostoru můžete s vektory šibovat, má jednu velkou výhodu. Můžete si vytvořit přímku - jeden z nejzákladnějších matematických objektů. Prostě se postavíte do bodu A, vyberete si nějaký ten vektor v a vyrazíte v jeho směru (tomu odpovídá tzv. parametrická rovnice přímky: x = A + tv, t∈R).
Na varietě vám to neprojde. Postavíte se do bodu p, vyberete si nějaký vektor v z tečného prostoru, vyrazíte v jeho směru a rázem jste mimo varietu, protože ty tečné vektory trčí „mimo“ a varietu obvykle rychle „opustí“ (stejně jako tečna ke kružnici hned za tečným bodem opustí kružnici). Tečný prostor TpM je tedy de facto prostorem mimoňů.
Přesto asi cítíte (pokud si představíte zeměkouli), že by neměl být problém vybrat si nějaký směr z tečného prostoru a pak vyrazit „podél variety“ tímto směrem s tím, že půjdete po varietě v rámci možností „furt rovně“ (představte si to jako pohyb kuličky, na kterou nepůsobí žádná síla). Směr vašeho pohybu se tím od původního vektoru sice nominálně odchýlí (nejprve nepatrně a posléze víc a víc), ale budete stále na varietě. Křivka, která vznikne tímto způsobem, se jmenuje geodetika a hraje na varietách roli přímky. Stejně jako ona má tu krásnou vlastnost, že je nejkratší spojnicí mezi dvěma body variety (letadla nelétají po přímkách, ale po geodetikách - tedy pokud zrovna pilot necítí potřebu vyhnout se nějaké bouřce). Kudy ta geodetika přesně vede, závisí na zakřivení variety a obvykle se to musí spočítat pomocí diferenciálních rovnic. Příslušný aparát se dá nejlépe realizovat na tzv. riemannovských varietách, kde se v těch tečných prostorech dá zavést skalární součin - což je případ většiny slušně vychovaných variet - a z něho se pak odvodí norma, metrika a element vzdálenosti.
Protože život na varietách se dá docela dobře zkoumat pomocí křivek, to, že tečné vektory jsou mimoňové, není zase taková tragédie. Přesto si matematici vymysleli způsob, jak je poměrně přirozeně identifikovat s body ležícími ve varietě, tedy jak je v jistém smyslu „ohnout“ zpátky do variety (to „ohnutí“ dává jakous takous představu, jakým způsobem se pojem délky přenese z tečného prostoru - kde máme normu definovanou skalárním součinem - do variety). Funguje to ale pouze lokálně (tj. v malém okolí bodu p).
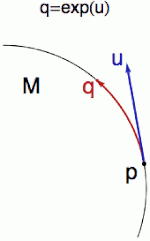
Vezměme si třeba kružnici (viz obrázek) s tečným vektorem u v bodě p. Pokud vektor nebude příliš dlouhý, tak „těsně pod ním“ na varietě najdeme bod, který by se mu dal přirozeně přiřadit. Představte si, že ten vektor u je vyroben z drátu. Trochu na něj zatlačíme prstem, on se ohne (ohne zu scherzen) a zabruslí do bodu q ležícího na varietě.
To přiřazení u → q se jmenuje exponenciální zobrazení (zřejmě aby to mátlo studenty) a používá se zejména v teorii Lieových grup (které reprezentují spojité symetrie a umožňují řešit některé problémy v klasické a kvantové mechanice).
Jen se musí definovat trochu rozumněji (ne pomocí ohnutého drátu): zvolíme si bod p na varietě M a nějaký vektor u z tečného prostoru TpM. Pak vyrazíme rychlostí u podél geodetiky určené tímto vektorem a v čase t = 1 do variety zapíchneme vlaječku. Ta bude reprezentovat bod q = exp(u). A je to.
Literární shrnutí: Bylo pravé poledne a arizonská poušť se koupala ve vlastním žáru. Starší honáci tomu říkali průtrž slunce. Jehly paprsků se zabodávaly do trsů aloe jako externí bodliny. Tanečnice Betty Lou seděla na verandě a přešívala si sukni pro večerní vystoupení ve varieté. Z protějšího baru U bídného kojota se zanedlouho vynořila vrávoravá postavička s kaktusem místo brady a zamířila k ní. Zdecimovaný kovboj se nejistě opřel o sloupek verandy a zahlaholil chraplavým basbarytonem: „Oh my darling Clementine... pocem opičko moje!“ Celou scénku pozoroval soustředěným pohledem i Krvavý Džejk odpočívající ve stínu nedalekého jasanu. Když se kovboj pokusil zdolat první schod verandy, vymrštil se k činu jako chřestýš. Vzduchem to zasvištělo a než bys řekl „bum“, opilý hulvát se válel v prachu ulice beznadějně zapletený do Džejkova lasa. „Vaše varieta má proklatě nízkou dimenzi, cizinče,“ zaskuhral zaskočený kovboj. Ale Džejk se nenechal vyvést z míry a aniž hnul jedinou brvou ve svém větrem ošlehaném obličeji, chladně odtušil: „Pokud preferujete vyšší dimenzi, mohl bych vás zabalit do celty nebo dehtového papíru.“ Neobratný chlípník se pokoušel vymanit ze smyčky. Betty Lou vyprskla smíchy: „Wow, takhle zauzlovanýho chlapa jsem na západ od Rio Grande snad ještě neviděla." Džejk jen mávl rukou: „Ve třech dimenzích ten uzel zvládne každý zelenáč. Ve čtyřech už by si na to netroufnul ani John Wayne.“ Betty Lou nasadila nechápavý výraz číslo 14 (ten se sladkou polevou, který tak ráda používala při svádění starosty McLintocka). „Přijďte za měsíc na obvyklé místo a já vám to vysvětlím,“ zaflirtoval Džejk a nenuceně zatahal za laso, aby opilce pobídl k přesunu do šerifovy kanceláře.
Addendum: Lebesgueova míra
Matematika si libuje v abstrakci. Studium n-rozměrných šipčiček zredukovala na vektorový prostor, studium křivek, zakřivených ploch a jejich vícerozměrných ekvivalentů proměnila v analýzu variet a stejným způsobem zatočila i s výpočtem velikostí různých podmnožin eukleidovských prostorů.
Kdy začnete zkoumat vlastnosti délek v 1D, obsahů v 2D, objemů v 3D a hyperobjemů ve více rozměrech, zjistíte, že mají leccos společného. Například pro dvě disjunktní (nepřekrývající se) množiny A a B platí:
m(AυB) = m(A) + m(B)
přičemž m může znamenat jak délku, tak obsah nebo objem - podle toho v jaké dimenzi pracujete. Aby se všechno nemuselo rozpracovávat třikrát, matematika si vymyslela míru) jakožto pojem, který v sobě zahrnuje všechny výše zmíněné speciální varianty.
Míra je tedy funkce, která dokáže jistým podmnožinám daného prostoru přiřadit nezáporné číslo, které vyjadřuje jejich velikost (ať je to délka, obsah či objem). Všimněte si, že říkám „jistým podmnožinám“. Teorie míry se sice snažila okruh množin, kterým lze rozumně přisoudit nějakou velikost, co nejvíce rozšířit, ale úplně všechny množiny se - ani při nejlepší vůli - změřit nedají. Tzv. neměřitelné množiny jsou ale většinou značně divoké a běžný smrtelník si s nimi nemusí lámat hlavu.
Nicméně známý Banach-Tarského paradox (který říká, že pevnou kouli v 3D prostoru lze rozložit na konečně mnoho kousků a ty pak přeskládat tak, že z nich dostanete dvě identické kopie původní koule) se opírá právě o neměřitelné množiny. Tady je krátký pdf souhrn v češtině, zajímavá diskuse v angličtině je zde anebo zde.
Stejně jako lze normu (tj. velikost) vektoru definovat různými způsoby, lze různými způsoby zavést i míru. Zlatým standardem v matematice je tzv. Lebesgueova míra, která je založena na pokrytí dané množiny spočetnými kolekcemi kostek. Její přesná definice je poměrně technická (Lebesgue se skutečně snažil posunout hranici měřitelných množin, kam až to šlo), ale laik si místo ní může i nadále představovat běžnou délku, obsah či objem.
Jedním z nejznámějších „zaklínadel“ moderní matematiky se stala fráze, že něco platí „skoro všude“. To obvykle znamená, že to platí pro všechny hodnoty s výjimkou množiny, jejíž celková míra je nula. A to nemusí být nutně úplně nicotná množina - např. racionální čísla mají nulovou míru: m(Q)=0.
Zajímavé také je, že moderní teorie pravděpodobnosti se stala odnoží teorie míry, protože se v podstatě zabývá měřením velikosti různých podmnožin jevového prostoru Ω, jehož celková míra je m(Ω) = 1.
Asi nejznámější aplikací Lebesgueovy míry je tzv. Lebesgueův integrál (který se stal zlatým standardem pro integraci funkcí, tedy zhruba pro agregaci jejich hodnot, resp. pro měření ploch pod jejich grafem). Ten se liší od Riemannova integrálu (který se obvykle vyučuje na technických školách) tím, že nerozřeže hledanou plochu na vertikální nudličky, které pak sečte, ale rozřeže ji na horizontální nudličky (na kterých je funkce zhruba konstantní, takže se dá lehce integrovat), těm přiřadí míru a tyto pak váženým způsobem sečte (podrobnosti i s obrázkem zde).
Článek je redakčně upravenou verzí blogového příspěvku na serveru iDNES.cz. Publikováno s laskavým svolením autora. Další díly a původní texty jsou dostupné na blogu Jana Řeháčka.