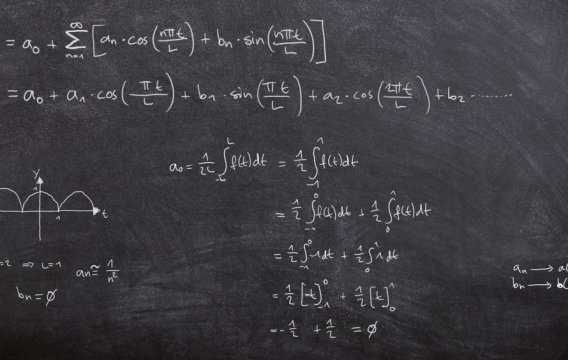Minkowského funkce je velmi zajímavá, ale příliš mnoho praktických aplikací nemá. Proto se dnes podíváme na funkce, které jsou sice poměrně jednoduché, ale v aplikacích matematiky zato prakticky nepostradatelné.

Matička příroda je milosrdná, a protože ví, že ne každý proces, do jehož realizace se zbrkle pustíme, se nám povede, dala nám možnost naše unáhlení odčinit procesem opačným - tedy inverzním. Když si omylem nasadíme botu, přestože se nikam nechystáme, můžeme si ji klidně zase zout (inverzní proces) a dostat se zpátky do výchozí pozice. Tedy bota nenasazena.

Inverzní procesy nás provázejí na každém kroku. Pokud posuneme květináč nalevo, můžeme ho zase vrátit zpět do výchozího postavení pošoupnutím napravo. Pokud si namažeme chleba sádlem, můžeme ho seškrabat stěrkou. Pokud něco zamkneme, můžeme to zase odemknout. Můžeme klidně odvolat, co jsme odvolali, a slíbit, co jsme slíbili. Zkrátka bez inverzních procesů by náš život vezdejší byl podstatně zašmodrchanější.

Podobná mechanika funguje také u funkcí, na které se můžeme dívat jako na určitý typ procesu, který ze vstupních hodnot vytváří hodnoty výstupní. Občas by se nám hodilo, kdybychom výstupní hodnoty mohli popadnout a vyčarovat z nich zpátky hodnoty vstupní. A k tomu slouží právě inverzní funkce. Vezměme si jako příklad hypotetický kuchyňský spotřebič Kašák, který ze všech vstupních hodnot vytvoří příslušnou kaši. Nasypete do něho brambory, dostanete bramborovou kaši. Nasypete do něj hrách a v cuku letu máte hrachovou kaši. Z krupice vám tento zázrak moderní techniky udělá kaši krupicovou.

Jenže co když nás dohoní mlsná a my bychom místo bramborové kaše raději hranolky. Z téhle kaše nám náš univerzální Kašák nepomůže. Tady bychom potřebovali jeho inverzní verzi, která z každé kaše vykouzlí původní ingredience. Tedy jakýsi Antikašák. Natlačíme do něho naši bramborovou kaši a sim-sala-bim – na výstupu inverzní funkce se nám objeví brambory, ze kterých si pak můžeme nakrájet kýžené hranolky. Taková funkce je samozřejmě podstatně komplikovanější než funkce původní. Schválně si vezměte pinzetu a zkuste z krupicové kaše vypreparovat ten původní balíček krupice. Není to žádná legrace, nota bene když musíte každé zrnko vyždímat. A za chvíli uvidíme, že jistá obtížnost je údělem inverzních funkcí i v matematice.

V dnešním Matykání se nejprve podíváme na jejich definici a některé základní vlastnosti, a pak se zaměříme na funkce exponenciální a jejich inverzní funkce - logaritmy.

Inverzní funkce

V předminulém Matykání jsme se na funkce dívali jako na černou skříňku s trpaslíkem, který nám ze vstupních hodnot vytvoří hodnoty výstupní podle nějakého předem daného postupu (algoritmu). Ten algoritmus si často můžete představovat jako pouhý vzoreček, do kterého trpaslík vstupní hodnotu prostě dosadí. Například u kvadratické funkce y = x² vhodíte do skříňky třeba 7 a na výstupu dostanete 49.

Zvídavé hlavičky se teď mohou zadumat nad opačným (inverzím) procesem a zeptat se, jak zkonstruovat funkci, která by vzala těch 49 a udělala z nich zpátky 7. A přesně na tuto otázku odpovídá funkce inverzní. Tu si představíme také jako skříňku s trpaslíkem (koneckonců i inverzní funkce je funkce jako každá jiná), který je telefonicky spojen s trpaslíkem původním, takže jeho výrobní proces je v jistém smyslu zrcadlovým obrazem procesu původního.

Teď o něco techničtěji (viz obrázek níže). Původní funkci f(x) označím červeně, její inverzi zeleně. Představme si, že máme číslo A, které vhodíme do původní funkce f(x), abychom na výstupu obdrželi číslo B. To pak vezmeme, vhodíme ho do funkce inverzní a dostaneme nazpět hodnotu A. Původní funkce tedy zobrazuje A na B, zatímco funkce inverzní zobrazuje B zpátky na A. Po aplikaci obou funkcí jsme tedy přesně tam, kde jsme byli na začátku. Stojíme před bedničkami s trpaslíky a máme v ruce číslo A.

(jak vidíte, inverzní funkce se značí „superskriptem“ ^-1)

Malý příklad: představme si funkci zadanou rovnicí y = 2x + 1 (tato funkce tedy zdvojí vhozenou hodnotu a přičte 1). Pro výpočet inverzní funkce z té formulky prostě vyjádříme x v závislosti na y (aby se nám prohodil význam vstupu a výstupu), což v našem případě bude x = (y-1)/2. Tato inverzní funkce tedy odčítá jedničku a pak rozpůlí to, co nám zůstane.

Můžete si zkusit, že tyto dvě funkce skutečně fungují tak, jak je popsáno na obrázku. Vhoďme třeba A=11 a původní funkce nám vyhodí B=23. To vhodíme do inverzní funkce a máme zpět našich 11. A protože to, jak si označíme proměnné, je jen na nás, inverzní funkce se obvykle převede do „standardního“ zápisu y = (x-1)/2 (tenhle krok studenty obvykle úplně rozhodí, ale vidíte sami, že obě funkce, ať jsou zapsané tak či onak, dělají to samé: odečtou jedničku a rozpůlí - klidně bychom to mohli zapsat jako č = (ň-1)/2 a pořád by to byla ta samá funkce - ale při takovém značení už bychom si asi zahrávali s přízní rodičů).

Průšvih nastane, když původní (červená) funkce pro dvě různá x vyhodí úplně stejné y. To pak inverzní trpaslík po zadání y neví, kterou z hodnot x vám poslat na výstup. Takovou neplechu dělá právě třeba kvadratická funkce y=x². Když do ní hodíte 2 nebo -2, tak vám v obou případech trpaslík vyhodí na výstupu 4. Jenže když tu 4 hodíte jeho inverznímu kolegovi (tomu s frňákem nalevo), tak on je najednou celej popletenej a honem neví, zda vám na výstup hodit 2 a nebo -2. Proto je při definici inverzní funkce potřeba funkci původní omezit (přesněji omezit její definiční obor), aby takové zmatení nevyvolávala.

To vede v matematice k následující definici. Funkcím, které dvěma různým hodnotám x (vybraným z případně mírně přiškrceného definičního oboru) vždy přiřazují dvě různé hodnoty y, říkáme funkce prosté. A to jsou přesně ty, pro které jsme schopni „invers“ sestrojit. Graficky poznáme prostou funkci tak, že každá vodorovná přímka protíná její graf maximálně jednou.

Jako příklad si opět vezměme kvadratickou funkci y=x², která na svém přirozeném definičním oboru prostá není (vodorovné přímky procházející nad osou x graf protnou dvakrát). Když ale omezíme definiční obor pouze na kladná čísla (červená část křivky), najednou je po problému. Takto přiškrcená funkce je prostá a inverzní trpaslík ví, co nám vrátit (této inverzní funkci říkáme odmocnina). Hodíme mu 4 a on nám vrátí 2, protože ví, že je inverzní funkcí pouze k té červené větvi (všimněte si, že červená větev už prostá je). Samozřejmě bychom si pro inverzi mohli vybrat i modrou větev a pak by nám inverzní trpaslík po vhození 4 nabídl -2. Graf takové inverzní funkce máte vpravo v modrém (y = - sqrt(x)). Dvě části paraboly vpravo jsou ve skutečnosti dvě různé funkce. Červená je inverzní k červené větvi kvadratické funkce a modrá k modré.

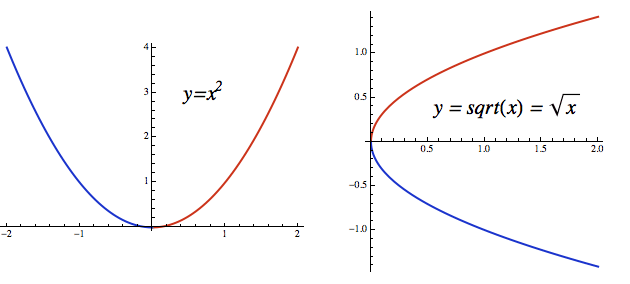
V jistém smyslu inverzní (zde odmocninový) trpaslík dělá toto. Vy mu na vstup vhodíte 7 a on okamžitě zavolá svému kolegovi (každý inverzní trpaslík s frňákem nalevo má přímou linku na originálního trpaslíka s frňákem napravo): „Hele, kámo, co bych ti tak musel hodit na vstup, aby na výstupu vypadla sedmička?“ Kámoš si pak chvilku hraje s těmi svými páčkami a čudlíky, občas kopne do parního generátoru čtverců a nakonec mu vyjde cca 2,64575... (což je přesně číslo, které umocněno na druhou hodí sedmičku). Toto číslo nahlásí inverznímu trpaslíkovi a ten nám ho vyhodí na výstupu. No a my mu říkáme odmocnina ze sedmi.

Z nějaké obecné mocniny - třeba 2³ - můžeme udělat funkci v podstatě dvojím způsobem. Buď si zafixujeme exponent (zde 3) a měníme základ (to číslo, které umocňujeme). V tom případě dostaneme mocniny - v tomto případě y=x³. Inverzními funkcemi k nim jsou potom příslušné odmocniny (samozřejmě poté, co vhodně otesáme definiční obor, abychom dostali prostou funkci - což je někdy celkem hustý výpočet).

Anebo si naopak zafixujeme základ, třeba 2 jako v příkladu nahoře, a budeme měnit exponent. Z něho se stane vstupní proměnná x. Takovým funkcím říkáme exponenciální funkce (exponenciely), a protože jejich inverzními funkcemi jsou právě obávané logaritmy, podíváme se na ně podrobněji.

Pochopitelně zvětšování exponentu (při konstantním základu) způsobuje daleko rychlejší růst než zvětšování základu (při konstantním exponentu), takže s exponencielami se setkáváme především tam, kde něco hodně rychle roste.

Exponenciální funkce

Asi nejjednodušší exponenciální funkcí je y=2^x (na obrázku níže v tmavozeleném). Její hodnoty v kladných celých číslech zvládneme prakticky z ruky: 2⁰ = 1, 2¹ = 2, 2² = 4, 2³ = 8 atd. Samozřejmě hodnoty pro ostatní exponenty už jsou trochu zapařenější, ale máme-li kalkulačku, zvládneme i tyto (pár poznámek o počítání s mocninami ponechám do sekce Jauvajs - z nich potom vyplyne, co „ostatní“ exponenty vlastně reprezentují).

Protože si za základ můžeme zvolit prakticky jakékoliv kladné číslo (se zápornými by byly trochu potíže), dostaneme potenciálně obrovské kvantum exponenciálních funkcí. Pár jsem jich vykreslil na následujícím obrázku, kde e je samozřejmě Eulerova slavná konstanta 2,71828... (číslo 3,89 žádnou slavnou konstantu nepředstavuje, ale přidal jsem ho tam, aby bylo jasno, že si skutečně můžeme vybrat jakýkoliv základ).

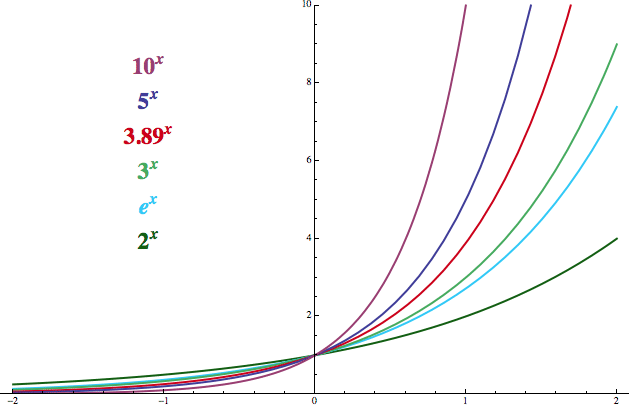
Sami vidíte, že funkce se sobě podobají takřka jako vejce vejci. Všechny mají podobné vlastnosti. Vyvstala tedy otázka, zda by se mezi nimi nedala vybrat jedna exponenciální funkce, kterou by matematici na celém světě mohli používat jako „zlatý standard“.

Teď asi doufáte, že si matematici vybrali tu se základem 10. Koneckonců běžně počítáme v desítkovém systému a mocniny 10 vám vysype každý solidní středoškolák: 10, 100, 1000 atd. Jenže matematici si jako svůj exponenciální standard vybrali funkci se základem e = 2,71828... Co je k tomu vedlo? Ono se totiž ukázalo, že exponenciální funkce se základem e má spoustu vlastností, které ostatní základy nemají. Ukážu vám jeden teoretický a jeden praktický.

Podívejme se nejprve na „standardní“ exponenciální funkci (někdy se značí exp(x)). Vidíte, že funkce nejen že neustále roste, ale také že čím je větší, tím roste rychleji. Tento růst se dá nejlépe kvantifikovat pomocí tečen (to jsou ty červené pahýlky přímek), které vystihují růst dané funkce v daném bodě. Každá tečna má svoji směrnici (v podstatě tangens úhlu té přímky) a čím je směrnice vyšší, tím tečna roste rychleji - a s ní i příslušná funkce (v daném bodě).

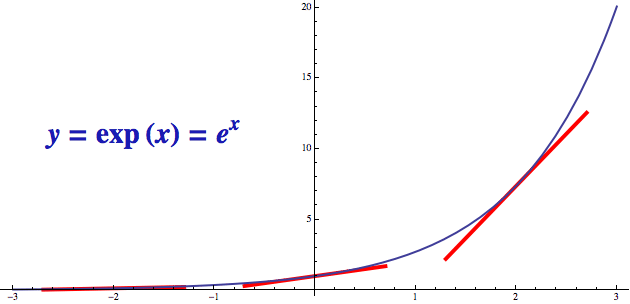
Z levé části grafu je vidět, že pro malé hodnoty y je růst celkem pomalý (tečna stoupá jen velmi líně), zatímco pro vyšší hodnoty y (graf vpravo) roste tečna poměrně rychle. Pro všechny exponenciální funkce platí, že jejich růst (směrnice tečny) je přímo úměrný nabyté výšce (tedy funkční hodnotě). Pouze pro jednu ale platí, že tempo růstu je získané výšce rovno přesně. A onou vyvolenou exponenciální funkcí je právě ta se základem e.

Ačkoli to může vyhlížet jako nepodstatný detail, této vlastnosti hojně využívají například diferenciální rovnice, které popisují celou řadu důležitých fyzikálních procesů.

Pro praktický příklad zabrousíme do sféry bankovnictví, přesněji do oblasti složeného úročení. Představte si, že máte základní částku Z = 1000 Kč a uložíte si ji na jeden rok s úrokem p = 10 % (v matematice používáme místo procent desetinné číslo u = p/100 = 0,1). Na konci tedy dostanete nazpět částku N = Z*(1+u) = 1100 Kč. Jenže pak si řeknete, co by se stalo, kdyby vám banka připsala za půl roku úrok 5 % (polovinu dohodnuté výše) s tím, že zbylých 5 % byste dostali po vypršení druhého půlroku. Na první pohled se zdá, že se nic nezmění, ovšem na ten druhý je vidět, že na konci roku dostaneme o něco víc, protože do druhého půlroku vstupujeme s částkou navýšenou o ten půl úrok.

Konkrétně dostaneme o dvě a půl koruny víc: N = Z(1+u/2)(1+u/2) = Z*(1+u/2)² = 1102,5. Pokud bychom trvali na úrokování 4x v roce (po každém kvartálu si připíšeme čtvrtinu dohodnutého úroku), dostaneme nazpět ještě víc: N = Z*(1+u/4)⁴ = 1103,81. Při měsíčním úrokování bychom úrok rozdělili na 12 dílů a aplikovali ho 12x: N = Z*(1+u/12)¹² = 1104,71. Čím kratší úrokové období, tím vyšší výnos (i když ne o moc). Bankéře by samozřejmě zajímalo, co by se stalo, kdybychom úrokovali spojitě (tedy číslo 12 v poslední formulce bychom nahrazovali vyššími a vyššími čísly). Velikost našeho účtu by se tím zvyšovala plynule. Úrok by nám nebyl připočítáván jednou za rok či měsíc, ale doslova každý okamžik. Matematicky to můžeme popsat limitou následujícího výrazu pro n blížící se nekonečnu - n nám udává, kolikrát budeme úročit (a Z na chvilku zapomeneme, aby nás to nerozptylovalo):

lim (1+u/n)ⁿ

v něm uděláme substituci n/u = k a do nekonečna pošleme k

lim (1+1/k)^k*u

Stačí tedy spočítat limitu

lim (1+1/k)^k

a to, co nám vyjde, pak umocnit na u (viz vzoreček 3 v sekci Jauvajs)

Když si do posledního vzorečku zkusmo dosadíte pár zvětšujících se hodnot k, zjistíte, že číslo, ke kterému budete postupně konvergovat, je právě Eulerovo číslo e. Pro roční výnos ze spojitého úročení proto platí velmi jednoduchá formulka: N = Z * e^u. Pokud se vrátíme k naší hodnotě 10 % (u = 0,1), při spojitém úročení bychom měli na účtu 1105,17 Kč. Pro r roků bychom pak stejným způsobem dostali vztah N = Z * e^{(u * r)}. To znamená, že při spojitém úročení roste náš základní vklad exponenciálně, a to se základem e (podrobnosti zde). A může za to právě výše uvedená limita (tou se Eulerovo číslo také často definuje).

Logaritmy

Logaritmus není nic jiného než inverzní funkce k exponenciální funkci. Každá exponenciela má samozřejmě svůj vlastní logaritmus s tím, že jako „zlatý standard“ opět používáme ten, který odpovídá základu e. Ten je inverzní funkcí k exp(x), říkáme mu přirozený logaritmus a značíme ho ln(x). Eulerovu číslu e se proto někdy říká základ přirozených logaritmů.

Na dalším obrázku máte všechny exponenciely shora invertované na logaritmy (ten přirozený je opět vyznačen světle modře). Základ daného logaritmu se obvykle vypisuje jako subskript.

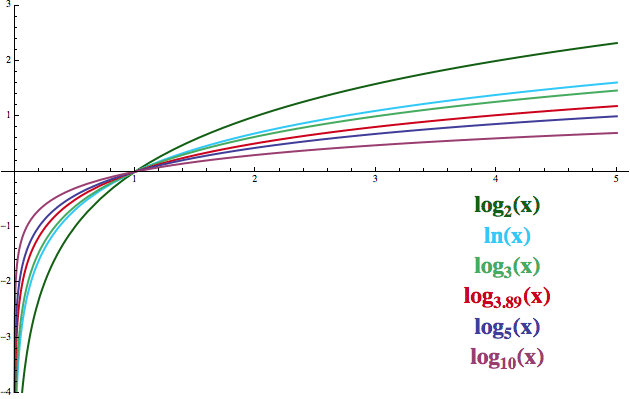
Protože exponenciela nám vždy vyhodí kladné číslo, nemělo by nás překvapit, že logaritmy jsou definované jen pro kladná čísla. Hodit inverznímu (logaritmickému) trpaslíkovi na vstup -3, by bylo to samé, jako zeptat se, co musíme vhodit do příslušné exponenciely, aby nám vyplivla -3. Nic takového ale neexistuje.

Abychom si ten logaritmus trochu osahali, podíváme se, jak funguje pod kapotou. Aby se nám to lépe počítalo, vyberu si logaritmus dvojkový a budu mu říkat lg(x). Funkce 2^x zobrazuje např. 3 na 8 (což je 2³) a to znamená, že lg(x) musí zobrazovat 8 zpátky na 3, tedy lg(8)=3, aby nám ten dvojtrpasličí obrázek nahoře štymoval. Obdobně 2⁰ = 1 a to znamená, že lg(1) = 0. Každý exponenciální tvar se dá přepsat pomocí logaritmu - např. 2⁹ = 512 nese stejnou informaci jako lg(512) = 9. Pro necelá čísla musíme samozřejmě použít kalkulačku. Rozmyslete si ale, jaký je význam čísla lg(3,7). Bude to takové číslo, které musíme vhodit do dvojkové exponenciely, aby nám z ní vypadlo 3,7 (tj. exponent dvojky, který nám po vyčíslení dá 3,7). Kalkulačka nám prozradí, že toto číslo je 1,88753 (pokud vaše kalkulačka nemá obecný logaritmus, pak vězte, že logaritmus o základu „a“ z čísla „x“ je roven ln(x)/ln(a) a můžete si ho spočítat sami).

To, že je logaritmus ln(x) inverzní funkcí k exponenciele exp(x), se v řeči rovnic vyjádří takto:

(A) exp(ln(x)) = x pro x>0

(B) ln(exp(x)) = x pro všechna reálná x

V obou případech nám rovnice říká, že pokud na danou hodnotu x aplikujeme danou funkci a vzápětí funkci inverzní, dostaneme nazpět původní hodnotu (to uvnitř vnější závorky je de facto výstup z původní funkce). Přitom je celkem jedno, na kterou funkci se díváme jako na původní a na kterou jako na inverzní. Logaritmus se dá definovat i jinak (např. mocninnou řadou) a přirozenou exponencielu pak můžeme chápat prostě jako jeho inverzní funkci. Tohle by nás nemělo překvapit: posunutí květináče nalevo a napravo jsou také vzájemně inverzní procesy a je celkem jedno, na který se díváme jako na ten „původní“).

+++++++++

Pro ty, kdo stále teskní, že jsme si pro základ přirozené exponenciely nevybrali dvojku nebo desítku, mám ještě jeden malý přesvědčovací argument. Ukážu vám, že přirozený logaritmus nám vypadne z jedné velmi přirozeně definované funkce F.

A zadáme si ji geometricky. Nejprve si nakreslíme graf převrácené hodnoty, tedy funkce y = 1/x (technicky je to hyperbola). Všimněte si, že toto je velmi jednoduchá a jednoznačná funkce - nemusíme v ní totiž šachovat s žádnými konstantami. To ale ještě není naše funkce F, kterou vám představím až pod obrázkem.

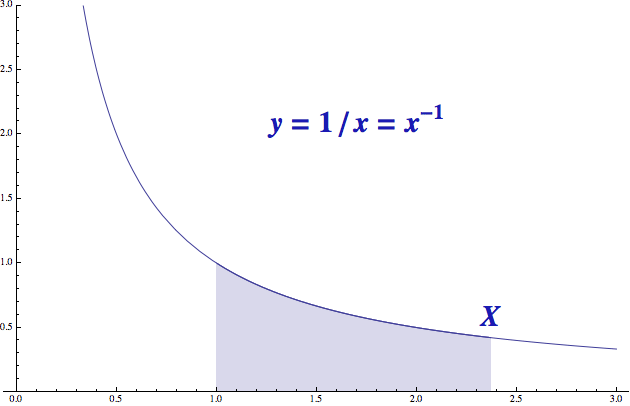
Teď si vybereme nějaké číslo X větší než jedna a vhodíme ho do naší tajemné funkce F. Trpaslík, který v ní bydlí, si zakreslí vystínovanou plochu od 1 do X. Spočítá její obsah a číslo, které mu vyjde, nám vyhodí na výstupu jako F(X). Velké X používám, aby se nám to nepletlo s proměnnou x té původní funkce.

Nemusí nás zajímat, jak trpaslík plochu spočítá. Kdo ovládá vyšší matematiku, spočítá si ji přes primitivní funkci. Kdo ne, může si výpočet představit tak, že trpaslík si plochu vystřihne z lepenky, zváží a váhu porovná s vahou jednotkového čtverce z téhož materiálu.

Opět zdůrazňuji, že tato funkce F(X) je velmi přirozeně definovaná. Není to žádné vykonstruované monstrum, ale plocha pod grafem celkem jednoduché funkce, v jejímž vzorečku navíc neplavou žádné externí konstanty, o které bychom se museli handrkovat s matikářem. Pro představu: na obrázku je hodnota X = 2,37 a když ji vhodíte tajemnému trpaslíkovi do bedničky, vyleze vám 0,86289 (to je ta vystínovaná plocha ve čtverečních jednotkách naznačených na ose x). Tipnete si, co je ta F za funkci? Je to přesně přirozený logaritmus X. Ne desítkový, ne dvojkový, ale ten Eulerův.

F(X) = ln(X), pro všechna X > 1.

A každý matematik hned po promoci přísahá logaritmu věrnost až za hrob.

A na závěr pár slov o tom, k čemu jsou ty logaritmy dobré. V první řadě bych poznamenal, že spousta procesů v našem vesmíru má exponenciální charakter (růst biopopulací, radioaktivní rozpad, složené úročení a obecně popis rychle rostoucích jevů) a při manipulaci s těmito funkcemi hrají logaritmy důležitou roli algebraických pomocníků. Např. řešení rovnice exp(0,5x) = 2 se provede tak, že na obě strany aplikujeme přirozený logaritmus (tj. logaritmus pravé strany se musí rovnat logaritmu levé strany) a ten tu exponencielu nalevo „sežere“ (jak mu velí výše uvedený vzoreček B). Dostaneme 0,5x = ln(2) a odtud x = 1,38629.

Důležitou vlastností logaritmu je, že převádí násobení na sčítání podle vzorečku

ln(x*y) = ln(x) + ln(y)

Na této formulce je mimochodem založeno logaritmické pravítko (sčítání se dá mechanicky simulovat posunutím pohyblivé střední části). Exponenciela naopak převádí sčítání na násobení: exp(x+y) = exp(x)*exp(y).

V dnešní době provádíme statistické modelování všech možných procesů (od vývoje na burze přes zpracování textů až po politický risk) a v těch vzorečcích se často objevují součiny různých veličin (to je u pravděpodobností dost obvyklé). Matematika je však vnitřně zařízena spíše na počítání se součty. Aby se součiny převedly na součty, uvažují se často logaritmy příslušných proměnných.

A konečně, logaritmus je výborný při vykreslování hodnot, které se mění v rozmezí několika řádů. Pokud byste dané údaje zobrazili realisticky, byl by jejich rozsah na ose y příliš velký a těžko by se z takového grafu něco vykoumalo. Proto se v takových případech používá logaritmická stupnice - na hodnoty se před vynesením aplikuje nějaký logaritmus. Ten hodnoty v podstatě „umravní“, tedy učiní jejich variabilitu snesitelnou, ale současně zachová jejich vzájemné vztahy - takže vrcholy vaší křivky budou stále tam, kde mají být. Například hodnoty, které se mění řádově od 1 do 1000, se po aplikaci desítkového logaritmu budou měnit pouze od 0 do 3. Takový graf se pak podstatně lépe čte.

Sekce jauvajs: Jak na mocniny?

technické opáčko ze střední školy pro ty, co ještě nemají dost

Většina poznatků o mocninách se dá shrnout do tří vzorečků.

(1) x^a * x^b = x^(a+b)
(2) x^a / x^b = x^(a-b)
(3) (x^a)^b = x^(a*b)

Ten první říká, že při součinu mocnin sčítáme exponenty. Ten druhý, že v podílu exponenty naopak odečítáme (tj. že ve zlomku se dá krátit), a ten poslední, že při mocnění mocniny exponenty prostě vynásobíme. Třetí vzoreček je v jistém smyslu zobecněním prvního. Všechny vzorečky se dají lehce ověřit tím, že si je rozepíšete. Tj. x^a je x * x * x...*x (to vše a-krát).

Nejdřív se podívejme, jak je to se slavnou nultou mocninou (vzoreček 2).

1 = x/x = x¹ / x¹ = x^(1-1) = x⁰

Tedy nultá mocnina je vždy jednička (pro nenulové x).

A co záporné exponenty? Zvolme si libovolné kladné číslo k.

1 / x^k = x⁰ / x^k = x^(0-k) = x^(-k)

Tedy záporné mocniny jsou převrácené hodnoty příslušných kladných mocnin (opět jsme použili vzoreček 2). A teď se podíváme, kolik by tak asi mohlo být x^(1/2). Platí:

x^(1/2) * x^(1/2) = x^{(1/2 + 1/2)} = x¹ = x (podle vzorečku 1)

To znamená, že číslo x^(1/2) má tu vlastnost, že když ho vynásobíte se sebou samým, dostanete x. To je ale přesně definice druhé odmocniny. Takže x^(1/2) = sqrt(x). A teď x^(1/3). Tady si pomůžeme vzorečkem 3.

(x^(1/3))³ = x^{(3 * 1/3)} = x¹ = x

Takže x^(1/3) je takové číslo, že když ho umocníme na třetí, dostaneme x. To je zase přesně definice třetí odmocniny. Obdobně si můžete ověřit, že x^(1/k) je prostě k-tá odmocnina z x.

Teď už tedy umíme umocnit x na libovolné racionální číslo p/q (vzoreček 3):

x^(p/q) = x^{(p * 1/q)} = (x^p)^(1/q)

to znamená, že x^(p/q) je q-tá odmocnina z p-té mocniny. Např.

x^(3/2) = sqrt(x³)

Když si x představíte jako základ exponenciální funkce, tak už ji umíme definovat pro všechna racionální čísla.

Pokud vás zajímá, jak se definuje mocnina pro iracionální exponent z, provede se to limitním trikem, který jsme viděli minule. Vybereme si tedy posloupnost racionálních bodů r, která k našemu exponentu z konverguje - v nich už mocninu spočítanou máme - a pak se podíváme, k čemu nám konvergují právě spočítané hodnoty x^r a to prohlásíme za hodnotu naší mocniny pro exponent z, tedy x^z (zde opět využíváme spojitost exponenciely).

S tím si ale nemusíme lámat hlavu, kalkulačka to udělá za nás a má na to svůj vlastní postup.

Článek je redakčně upravenou verzí blogového příspěvku na serveru iDNES.cz. Publikováno s laskavým svolením autora.

Další díly a původní texty jsou dostupné na blogu Jana Řeháčka.

Autor: Jan Řeháček