Ve většině matematických disciplín hraje centrální roli pojem funkce. Jednu z nejzajímavějších navrhl v roce 1904 Hermann Minkowski a pro charakteristický tvar jejího grafu jí někdy říkáme „kluzké ďáblovo schodiště“.
Prvořadým úkolem matematiky je připravovat infrastrukturu, která by ostatním vědám umožnila popsat svět kolem nás. K nejdůležitějším fenoménům, které přírodní vědy při svém šťourání do hlubin Vesmírovy duše odpozorovaly, patří souvztažnost určitých veličin, tedy z pohledu matematiky závislost mezi dvěma kvantitami (čísly).
Vezměme si třeba kámen, který určitou silou vyhodíme do vzduchu. Není těžké přijít na to, že vzdálenost dopadu kamene závisí na úhlu, pod kterým ho vymrštíme. Když ho vyhodíme příliš kolmo, daleko nedoletí. Když ho vymrštíme horizontálně přímo před sebe, nebude to o moc lepší. Nejlepší je hodit ho zhruba pod úhlem 45 stupňů. Pak letí opravdu daleko (navzdory úsloví „je to, co by kamenem dohodil“). Jedním z možných způsobů, jak tento proces uchopit, je sestavení tabulky, která by nám řekla, jak daleko – pro daný úhel výhozu – kámen doletí. Ještě lepší je však závislost mezi úhlem a vzdáleností zakódovat pomocí algebraických operací do mechanismu funkce a pomocí tohoto zakódování potom daný jev systematicky studovat. A právě o tom bude dnešní Matykání.
Nejprve vám ukážu jednu z možností, jak se na funkce dívat, pak bude malé opáčko ze střední školy a nakonec se podíváme na slíbenou funkci Hermanna Minkowského. Ten, kdo si něco o funkcích pamatuje z gymnázia, může první dvě části přeskočit a jít rovnou k Sekci jauvajs, kde dnešní příspěvek de facto začíná.
A nejhorší ze všeho jsou trpaslíci...
Na funkce se můžeme dívat mnoha různými způsoby. Já osobně mám nejraději následující pohled.
Představme si funkci jako černou skříňku, která má jeden vstup (in), kam budeme vhazovat čísla, a jeden výstup (out), odkud budeme čísla odebírat (a ne aby do toho vstupu někdo nacpal žvejkačku!). Uvnitř skříňky je zavřený trpaslík, který má přesné instrukce, jak s vhozeným číslem naložit.

Může ho třeba umocnit na druhou a přičíst k němu dvojku nebo ho interpretovat jako úhel a spočítat jeho kosinus. Důležité však je, aby nám pro každou vstupní hodnotu vyhodil na výstup jenom jedno číslo. Nebo žádné - v tom případě říkáme, že funkce není pro daný vstup definovaná. Vhozenému číslu říkáme nezávisle proměnná a obvykle ho značíme písmenkem x. Číslu, které nám trpaslík vyhodí ven, říkáme naopak závisle proměnná a značíme ho většinou písmenkem y (to je však jen konvence - používat můžete libovolná písmenka). V příkladu z úvodu by x reprezentovalo úhel vrhu a y pak vzdálenost dosaženou kamenem.
Protože by se obrázek s trpaslíkem asi těžko tiskl do skript, v praxi používáme úspornější značení:
y = f(x)
které nám říká, že proměnná y je funkcí proměnné x; funkci zde značíme písmenkem „f“. Také bychom rovnici mohli popsat tak, že y je funkční hodnotou v bodě x. Anebo že jsme na hodnotu x aplikovali funkci f a obdrželi tak hodnotu y.
Pokud chceme zdůraznit, že víme, co trpaslík ve skříňce dělá, můžeme funkci zapsat explicitně:
y = 2 + x2
Jindy se používá zápis pomocí šipky:
f: x --> y popřípadě explicitně f: x --> 2 + x2
který znamená, že funkce f zobrazuje hodnotu x na hodnotu y. Takto definovaná funkce (tedy de facto proces, který trpaslík při počítání výstupní hodnoty používá) odráží určitý konkrétní vztah mezi dvěma veličinami, což je přesně to, co vědci ke své práci potřebují. Plus propisku a asi dvě tuny papíru.
Každá funkce má svůj přesně stanovený definiční obor, což je množina čísel, pro které je trpaslík ochoten něco na ten výstup vyhodit. Všechna ostatní čísla prostě ignoruje. Pokud není stanoveno jinak, používáme tzv. přirozený definiční obor, který odpovídá situaci, kdy trpaslík akceptuje všechna čísla, pro která má daný proces smysl. Např. pokud trpaslík z každého čísla udělá převrácenou hodnotu (tedy x --> 1/x), je jasné, že dovnitř můžeme vhodit cokoliv kromě nuly (tou se nedělí ani v neděli!). Přirozeným definičním oborem takové funkce je tedy množina všech reálných čísel s výjimkou nuly. Pokud si však postavíte hlavu a do skříňky nulu přesto vhodíte, trpaslík vyběhne ven a dá vám do držky.
Někdy se však vyplatí definiční obor uměle zúžit, např. proto že chceme z fyzikálních, pedagogických nebo jiných důvodů omezit množinu čísel, se kterými daný trpaslík pracuje. Minkowského funkce, ke které směřujeme, se např. dá definovat pro každé reálné číslo, ale já ji budu v tomto článku uvažovat pouze na intervalu (0,1), abychom se nemuseli rozptylovat podružnými detaily.
A teď ještě v rychlosti pár slov o dvou důležitých vlastnostech funkcí. Představme si, že trpaslíkovi postupně vhodíme do skříňky dvě čísla, která se od sebe moc neliší. Protože v přírodě se věci nemění skokem, ale pozvolna, očekáváme, že dvě čísla, která nám trpaslík na výstupu nabídne, se od sebe také nebudou moc lišit. Pokud tomu tak skutečně je, říkáme, že funkce je „spojitá“.
Pokud do skříňky sypeme čísla, která jsou stále větší a větší, a trpaslík nám na výstupu také vrací větší a větší hodnoty, říkáme, že funkce je „rostoucí“. Pokud je tomu naopak a s rostoucí hodnotou x se příslušné hodnoty y na výstupu zmenšují, mluvíme o funkci „klesající“.
Tyto dvě definice sice nejsou zcela přesné, ale dají nám jakous takous představu, co pojmy znamenají. Přesnější definice spojitosti a monotonie jsou poměrně technické.
Omezme se teď pouze na kladná čísla. Jako ukázku rostoucí funkce si můžete představit kvadratickou funkci y = x2 (tedy vhodíte číslo a trpaslík vám vyhodí jeho čtverec). Čím větší číslo vhazujete, tím větší bude jeho čtverec na výstupu. Typická klesající funkce je již zmíněná y = 1/x. Čím větší je číslo na vstupu, tím menší bude jeho převrácená hodnota. Obě funkce jsou (pro kladná čísla) spojité. Ta druhá je ovšem nespojitá v nule (pokud zrušíte omezení na kladná čísla).
Opáčko: Trojjediná povaha funkcí
Ve škole se toho o trpaslících samozřejmě moc nedozvíte. Seriózní matematika se na funkce dívá daleko formálněji, a to hned trojím způsobem. Můžete si je představit jako výrobní postup, jako graf anebo jako tabulku hodnot.
Tyto tři způsoby si ukážeme na jednoduchém příkladu. Představme si, že v ruce držíme kámen a v čase x = 0 ho upustíme do studny. Sestrojíme si funkci, která bude popisovat hloubku dosaženou kamenem. Vstupní veličina x bude čas a na výstupu nám trpaslík vrátí číslo y, které nám řekne, do jaké hloubky se v daném čase kámen propadl.
1. První možností je dívat se na funkci jako na předpis, jak hodnotu f(x) z hodnoty x spočítat (obvykle to je vzoreček nebo kombinace vzorečků). Je to vlastně jakási „trpaslíkova kuchařka“. V našem konkrétním případě je krmě celkem stravitelná:
y = 0 pro x<=0
y = -x2 pro x>0
(pro jednoduchost jsem ve vzorečku potlačil některé fyzikální konstanty)
První výraz odráží skutečnost, že kámen upustíme až v čase x = 0, takže do té doby je dosažená hloubka 0. Druhá část vyjadřuje známý fakt, že při volném pádu narůstá hloubka se čtvercem času.
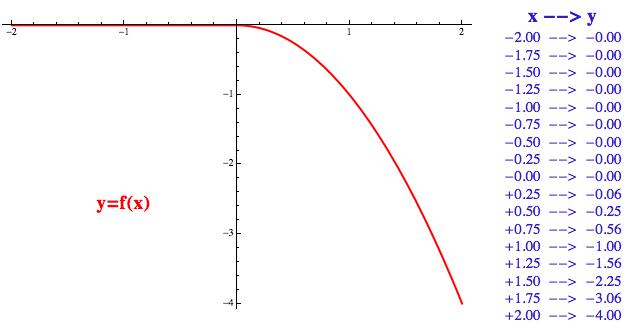
2. Druhá – a velice populární – možnost je na funkce pohlížet prostřednictvím jejich grafů (dole na obrázku vlevo a červeně). Ty zkonstruujeme tak, že ke každé hodnotě x, kterou trpaslíkovi vhodíme do bedny, přiřadíme výstupní hodnotu y, a dostaneme tak de facto souřadnice nějakého bodu B = (x,y). Když všechny takto obdržené body vyneseme v běžné rovině x-y, dostaneme graf funkce, který nám vizuálně ukazuje, jakým způsobem se závisle proměnná y mění s hodnotou x. Na obrázku opět vidíme, že až do času x = 0 se nic neděje a pak se kámen začne propadat do hlubších a hlubších hodnot (to, že je křivka stále prudší, je jen odrazem faktu, že volný pád je rovnoměrně zrychlený pohyb – kdyby se padalo konstantní rychlostí, nepotřebovali bychom padáky).
3. Třetí možnost, jak si funkce představovat, je proměnit je v tabulku hodnot x a y (na obrázku vpravo a modře) s tím, že levý sloupek si volíme a ten pravý nám potom trpaslík dopočítává. Funkční hodnoty zde vidíme přímo napsané, nemusíme je z grafu luštit. Čím více hodnot x zadáme, tím přesnější informaci o chování funkce budeme mít.
Zda si danou funkci interně představujete jako předpis, graf nebo tabulku, je
více méně na vás. Každý má ta kolečka v hlavě nastavená jinak.
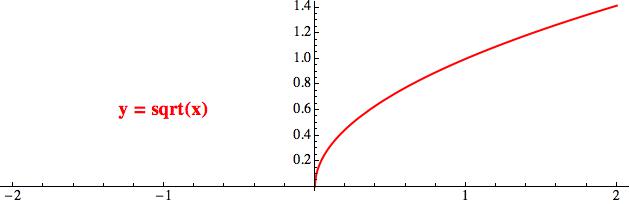
A na závěr této sekce ještě dva rychlé příklady. Tím prvním je funkce „odmocnina“. Jejím přirozeným definičním oborem je množina nezáporných čísel, protože pro záporná se odmocnina spočítat nedá (alespoň ne v reálném oboru). Je to funkce spojitá a rostoucí (to je z grafu krásně vidět). Je dokonce ostře rostoucí, protože pro větší hodnoty x dostaneme také větší y (ve smyslu ostré nerovnosti).
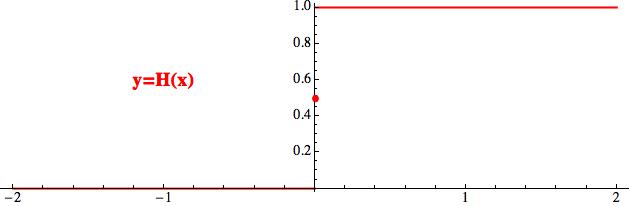
A ještě příklad funkce nespojité. Tato se nazývá Heavisideova funkce a používá se při popisu dějů, které se skokově mění (např. když
zapnete elektrický proud nebo jednorázově změníte hodnotu nějaké
veličiny). Všimněte si, že když trpaslíkovi předhodíte 0, vrátí vám
1/2. Když teď vstupní hodnotu malinko šoupnete a trpaslíkovi vhodíte
třeba číslo x = 0.00001, příslušná výstupní hodnota se změní velmi
dramaticky na y = 1. To je přesně obsahem pojmu (ne)spojitosti. Z grafu
nespojitost poznáte tak, že je jakoby „přetržený“, tedy nelze jej
nakreslit „jedním tahem“.
Sekce jauvajs
Spousta studentů si myslí, že funkce je vlastně jenom vzoreček, do kterého se dosadí a je po ptákách. Proto jsem jako ukázku vybral Minkowského funkci, která se dá definovat geometricky (přes vzoreček by to šlo taky, ale zamotali bychom se při tom do nekonečných řad). A pro jednoduchost ji budu uvažovat pouze na intervalu (0,1).
Tato funkce má nejen zajímavé vlastnosti (podíváme se na ně v závěru), ale také označení. Zatímco pro pojmenování většiny funkcí používáme písmenka, popřípadě zkratky – jako např. f(x), sin(x), arctg(x), log(x), sqrt(x) atd. – pro Minkowského funkci se vžilo označení pomocí otazníku, tedy y = ?(x). Pokud tedy Minkowského trpaslíkovi předhodíte číslo 2, na výstupu dostanete hodnotu ?(2). Proto se také této funkci někdy říká „otazníková funkce“ (Minkowski's Question Mark Function), přestože s otazníkem jako takovým nemá nic moc společného. Ale zase je poměrně tajuplná, takže toto označení celkem sedí.
Definice Minkowského funkce ?(x)
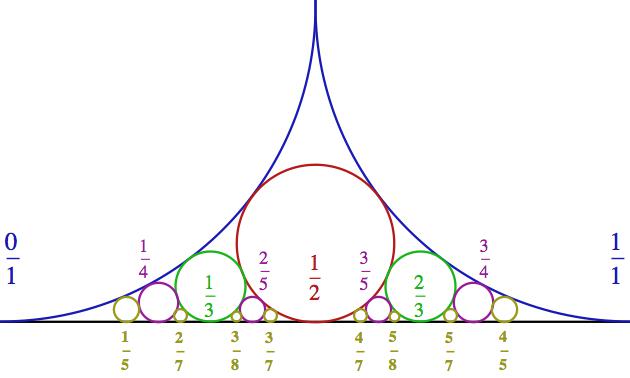
Abychom přesně pochopili, co trpaslík v Minkowského funkci s vhozeným číslem vlastně provádí, vrátíme se k jednomu starému Matykání a připomeneme si, že zlomky se na intervalu (0,1) dají zkonstruovat tak, že do nuly a jedničky navalíme dvě kružnice a potom do vzniklých mezer mezi nimi a „podlahou“ neustále vpisujeme nové kružnice a zapisujeme si, kde se dotknou osy x (spodní černá čára).
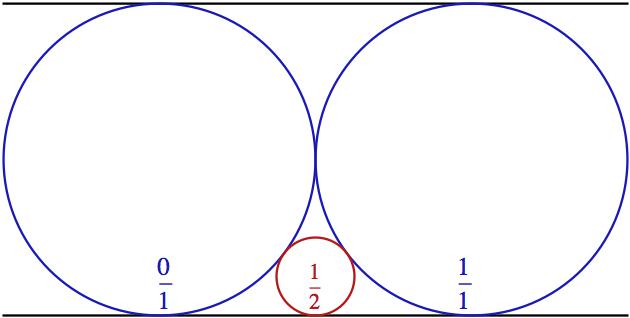
Ukázalo se, že místa dotyku přesně odpovídají racionálním číslům -
tedy zlomkům. Na obrázku, který je výřezem předchozího, jsem je
explicitně vyznačil v odpovídající barvě.
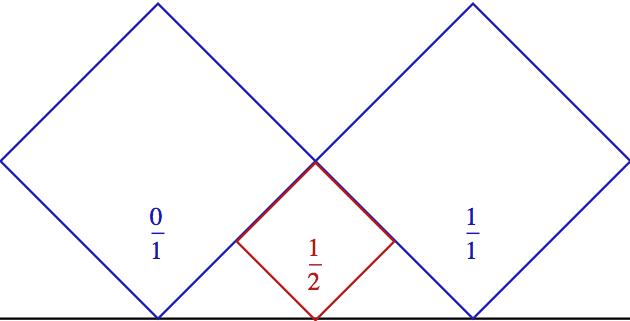
Ale to není všechno – pro geometrickou interpretaci Minkowského funkce si ještě musíme udělat jednu podobnou konstrukci. Princip bude stejný, jen s tím rozdílem, že na jednotkový interval nenavalíme kružnice, ale natlačíme na něj dva modré kosočtverce - jeden posadíme opět do nuly a druhý do jedničky. Do vzniklých mezer - stejně jako v předchozím případě - pak budeme dál vpisovat menší a menší kosočtverečky. A nehihnějte se tam vzadu!
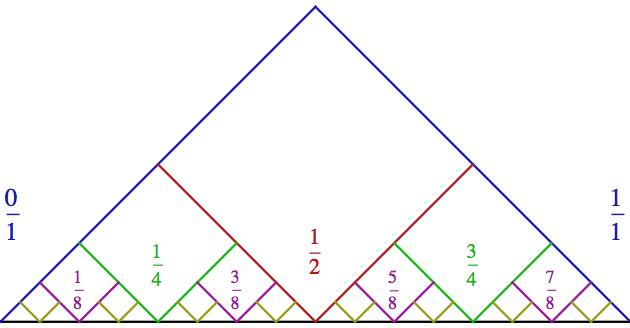
Aby do toho bylo lépe vidět, ukážeme si opět detail, ve kterém ze
základních modrých kosočtverců zůstala už jen jihovýchodní (pro ten v bodě 0), respektive jihozápadní (pro ten v bodě 1) stěna. U kosočtverců
máme výhodu, že nemusíme dělat žádnou komplikovanou matiku. Přímo z obrázku vidíme, že dva zelené kosočtverce (které vepíšeme po obou
stranách toho červeného) sedí v bodech 1/4 a 3/4. Ony totiž dělí ten
zbývající prostor přesně na polovinu (u kružnic to neplatí). Další
(fialová) generace kosočtverců pak sedí v osminách, následující
(žlutá) v šestnáctinách a tak dále.
Teď si finální mnohobarevné obrázky ještě převedeme na schematické
diagramy, které budou zaznamenávat pořadí, v němž jsme kružnice, resp.
kosočtverce vepsali. A také jejich vzájemnou polohu. To aby nám definice
Minkowského funkce šla později lépe od ruky.
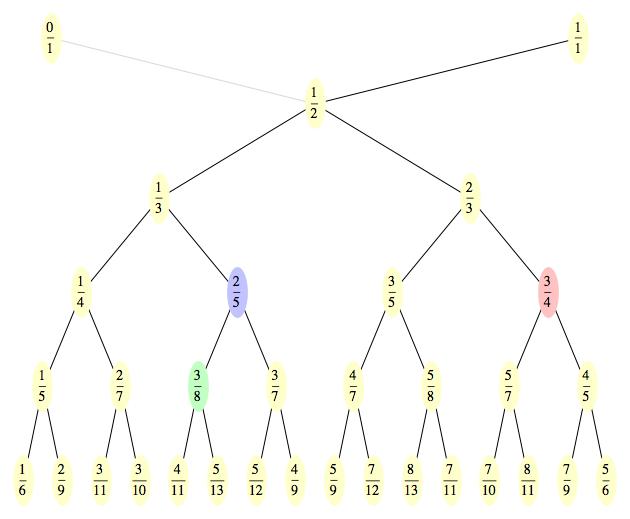
Diagram pro kružnice už jsme jednou viděli, říká se mu Stern-Brocotův strom, takže ho jenom v rychlosti připomenu (barvu oválků zatím ignorujte - pro tuto chvíli si je všechny představte jako béžové). První řádka reprezentuje dvě základní kružnice. Z nich vznikla ta sedící v 1/2. Na dalším řádku jsou pak body odpovídající zeleným kružnicím (sedící v 1/3 a 2/3), následují kružnice fialové (1/4, 2/5, 3/5, 3/4), žluté (1/5, 2/7,...) atd.
Totéž si uděláme pro obrázek s kosočtverci. Opět do první (horní) řady
posadíme dva základní modré kosočtverce, pod ně pak ten, co sedí v bodě
1/2, a pak dva zelené (1/4 a 3/4), čtyři fialové (v osminách) atd.
Všimněte si, že ve jmenovateli mají všechny zlomky mocninu dvojky. Takto
vzniklý strom budu v dalším textu nazývat dyadický.
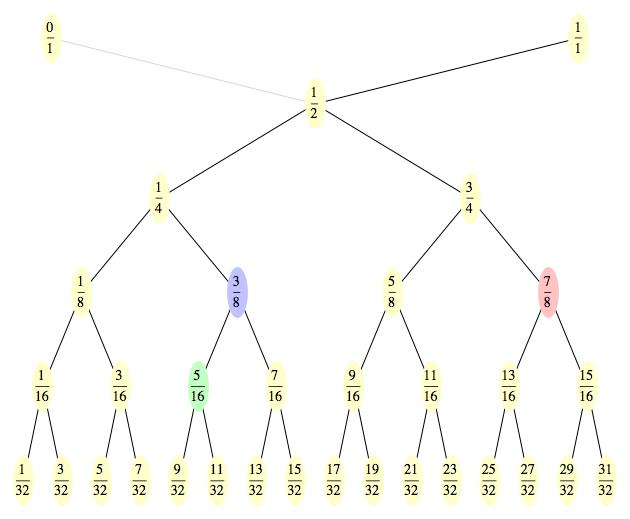
Oba stromy samozřejmě pokračují směrem dolů až donekonečna.
Na první pohled je vidět, že Stern-Brocotův strom má úplně stejnou strukturu jako ten dyadický. Vlastně se liší pouze nominálně v konkrétních hodnotách jednotlivých uzlů. Každému uzlu prvního stromu odpovídá přesně jeden uzel toho druhého. Například modrý uzel 2/5 na prvním stromu odpovídá na druhém stromu modrému uzlu 3/8. Korespondenci potvrzuje i fakt, že k oběma uzlům vede z bodu 1/1 stejná cesta (shora dolů: doleva, doleva a doprava). A stejně tak si odpovídají i ostatní uzly (viz zelený a červený). A právě tato přirozená korespondence mezi oběma stromy je kostrou Minkowského funkce.
Teď si ji konečně můžeme definovat (ale zatím jen pro zlomky). Pokud trpaslíkovi vhodíte do otvoru nějaké racionální číslo, on si ho nejdřív vyhledá na Stern-Brocotově stromu, zapamatuje si cestu k němu, a tu pak zopakuje na stromu dyadickém. Jinými slovy, trpaslík na dyadickém stromu vyhledá odpovídající číslo (tedy sedící na stejném „fleku“) a to vám hodí na výstup. Pokud umíte hledat v binárních stromech, je to brnkačka.
Příklad: na vstup hodíme trpaslíkovi racionální číslo 7/10. To najdeme v šesté řadě Stern-Brocotova stromu a z jedničky se k němu dostaneme takto: doleva, doprava, doprava, doleva a doleva. A teď si tu samou cestičku projdeme v dyadickém stromu a dostaneme se do odpovídajícího čísla na šesté řadě, což je 25/32. A to je také hodnota, kterou nám trpaslík hodí na výstup. Takže Minkowského funkce v bodě 7/10 se rovná 25/32. Symbolicky to můžeme zapsat jako ?(7/10) = 25/32. Jinými slovy, Minkowského funkce zobrazuje bod 7/10 na 25/32. Na procvičení si můžete z obrázků odvodit, že hodnota Minkowského funkce v bodě 2/7 jsou 3/16, tedy symbolicky ?(2/7) = 3/16.
(zbytek této podsekce je poměrně technický a můžete ho klidně přeskočit)
Zatím jsme funkci definovali pouze pro racionální čísla a někdo by se mohl dotázat, co se stane, pokud trpaslíkovi předhodíme nějaké iracionální číslo z intervalu (0,1). Například sqrt(2)-1, což je bratru nějakých 0.414214...
V takovém případě se funkce dodefinuje „ze spojitosti“. Nebudu vás zatěžovat technickými detaily tohoto procesu, ale ukážu vám jednoduchý příklad, jak se to dělá. Každé iracionální číslo se dá libovolně přesně aproximovat čísly racionálními (pro které už Minkowského funkci spočítat umíme) a má-li být výsledná funkce spojitá, funkční hodnoty v racionálních číslech by se měly přibližovat k (zatím neznámé) hodnotě v zadaném iracionálním bodě.
Vezměme si příklad, který cituji výše: sqrt(2)-1. Řetězový zlomek čísla je {0,2,2,2,2,2...} a dobré racionální aproximace x (viz zde) získáme useknutím tohoto nekonečného rozvoje. Následující tabulka nám ukazuje prvních pár racionálních aproximací (včetně řetězového zlomku a desetinné hodnoty) a jejich hodnotu y na výstupu z Minkowského funkce (včetně desetinné hodnoty).
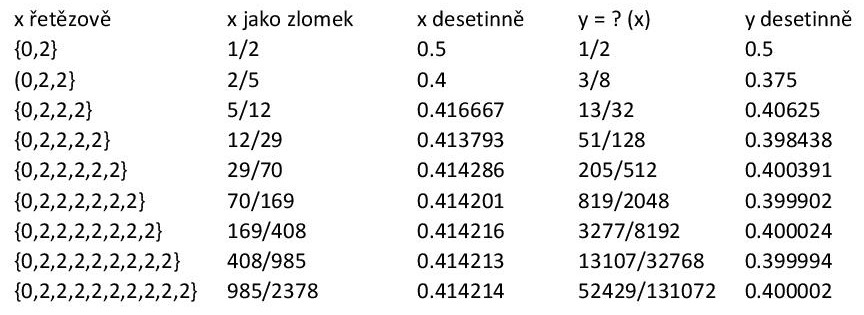
My vlastně ve druhém sloupci zadané iracionální číslo aproximujeme
přesnějšími a přesnějšími zlomky (pro které Minkowského funkci umíme
spočítat vyhledáním na stromu) a přitom doufáme, že ve čtvrtém sloupci
uvidíme přesnější a přesnější hodnotu Minkowského funkce v tom daném
bodě (to nám garantuje právě spojitost). Takže jak se nám zlomky ve
druhém sloupci postupně blíží k zadanému iracionálnímu číslu, hodnoty
na výstupu se blíží hledané hodnotě - v tomto případě 0.4, což jsou
2/5. Proto můžeme symbolicky uzavřít, že ?(sqrt(2)-1) = 2/5. Tedy
Minkowského funkce v tom bodě nabývá hodnotu 2/5.
(Já vím, úplně v tom bodě 0.4 ještě nejsme, ale taky jsme zatím udělali jen 9 aproximací. Trpaslík má čas tabulku protáhnout až donekonečna a tam to 0.4 uvidí přesně.)
To, že nám z kvadratické iracionality vypadl na výstupu zlomek, není náhoda. To platí obecně - kdykoliv vhodíme na vstup kvadratickou iracionalitu (tedy řešení kvadratické rovnice s celočíselnými koeficienty), Minkowského funkce nám na výstupu vyplivne racionální číslo! Ovšem ukázat to není žádná hračka - toho vás ušetřím. Tady je místo toho pár příkladů:
?(1+sqrt(3)) = 20 / 7
?(sqrt(11)-2) = 91 / 73
?(sqrt(15)) = 507 / 127
?((2 + sqrt(5))/7) = 15035090291654656 / 24019198012642645
Graf Minkowského funkce ?(x) na intervalu (0,1)
Teď, když umíme hodnotu Minkowského funkce spočítat pro každé číslo, můžeme se podívat na její graf. Prostě si z jednotkového intervalu vybereme haldu x-ových hodnot, trpaslík nám k nim dopočítá příslušná ypsilonka (funkční hodnoty) a takto vzniklé body (x,y) vyneseme do grafu. Vypadá takto:
Minkowského funkce ?(x) ... kluzké ďáblovo schodiště
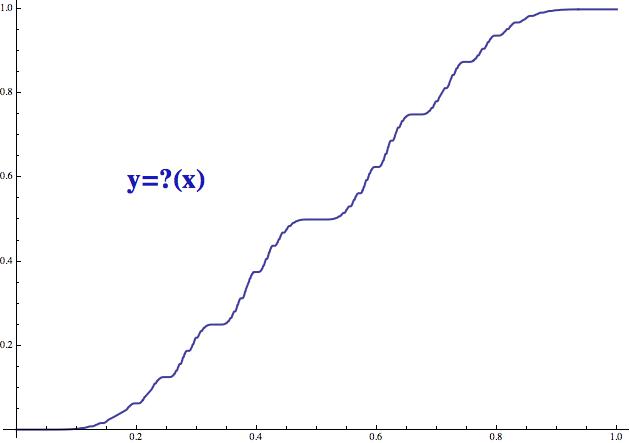
Pokud vás zajímá, proč se této funkci říká „kluzké ďáblovo
schodiště“, ukážu vám ještě funkci, které se říká „ďáblovo
schodiště“, a hned to bude jasnější. Tuto funkci vymyslel Georg Cantor a konstruuje se pomocí Cantorovy množiny, kterou jsme shodou okolností
promrskali v minulém Matykání.
Opět budeme na jednotkovém intervalu hledat prostřední třetiny, ale
tentokrát je nebudeme vyhazovat, ale narýsujeme nad každou z nich takovou
malou plošinku (a to ve výšce, která vždy rozpůlí zbývající interval
na ose y - tedy ta první plošinka uprostřed bude ve výšce 1/2, druhé dvě
po stranách v 1/4 a 3/4 atd.). Kam „prostřední třetiny“ nedosáhnou
(což je v podstatě Cantorova množina), tam opět dodefinujeme funkci ze
spojitosti. „Ďáblovo schodiště“ se této funkci říká proto, že její
graf má v jistém smyslu nekonečně mnoho schodů (plošinek) - všechny je
ovšem z důvodu konečného rozlišení obrazovky neuvidíte. Tady ji máte (a
všimněte si, že největší plošinka se skutečně rozpíná nad první
vyhozenou třetinou - tedy od 1/3 do 2/3):
Cantorova funkce c(x) ... ďáblovo schodiště
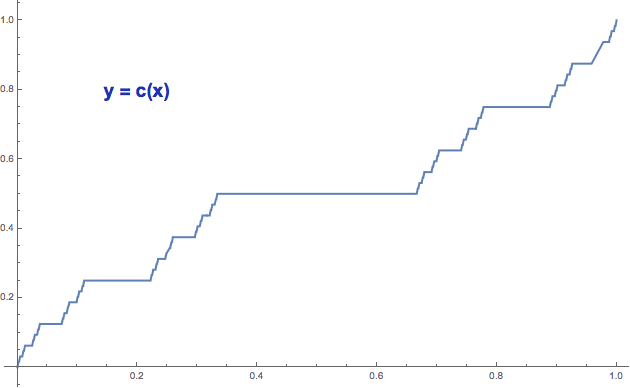
Když si dva grafy porovnáte, zjistíte, že jsou si velice podobné
(přestože jejich konstrukce se konceptuálně o dost liší). Každý má
uprostřed „plošinku“, pak po stranách dvě menší plošinky, mezi nimi
pak čtyři ještě menší a tak dále. Rozdíl je v tom, že u Cantorovy
funkce jsou plošinky opravdu vodorovné (části Cantorovy funkce jsou
konstantní), zatímco u Minkowského funkce neustále stoupají
(funkce je ostře rostoucí - kdykoliv si vyberete dvě čísla x<y,
platí pro ně ?(x)<?(y), bez výjimky). Takže když na to Minkowského
schodiště naprší, bude se pěkně smekat.
Vlastnosti Minkowského funkce ?(x)
Na závěr si ukážeme dvě zajímavosti spojené s touto funkcí.
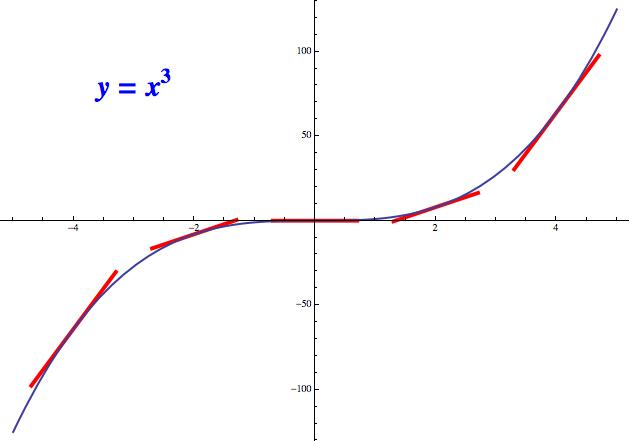
Nejdříve se podívejme na běžnou kubickou funkci y = x3. Tato funkce na celém svém definičním oboru roste (jejé graf tedy při pohledu zleva doprava stoupá). Rostou tedy i tečny k této křivce - tečnu si představte tak, že k funkci co nejtěsněji přiložíte červené „prkýnko“. Výjimkou je zde pouze bod x = 0, kde se růst „na okamžik zastaví“, takže tečna je vodorovná. U většiny slušně vychovaných ostře rostoucích funkcí není těchto zastavení moc. Taková funkce si prostě na svém definičním oboru dá jedno dvě kafíčka a už zase šupajdí výš.
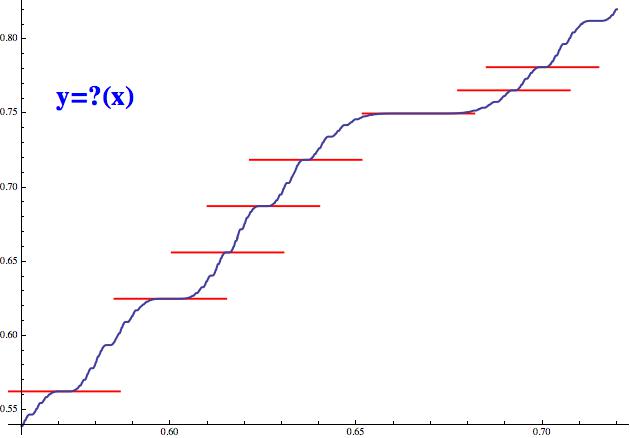
Minkowského funkce také neustále roste, ale má tu vlastnost, že její růst
se „na okamžik zastaví“ v každém racionálním bodě! Tedy její tečna
je ve všech racionálních bodech vodorovná! Na obrázku, který ukazuje
výřez celkového grafu, jsem to sice znázornil jen pro několik vybraných
bodů, ale nezapomeňte, že interval (0,1) je racionálními čísly hustě
posetý. Graf funkce tedy na jednu stranu jede vytrvale nahoru, ale současně
taky doslova každou chvíli zastavuje (je to prostě takový řidič typu brzda
- plyn).
Kdo ovládá vyšší matematiku, může si to vyložit tak, že
Minkowského funkce (přestože je spojitá a ostře rostoucí) má nulovou
derivaci ve všech racionálních bodech (!!!) - to sice není úplně zřejmé,
ale intuitivně se to dá pochopit takto: představte si nějaký konkrétní
bod Y = ?(X). Pozice bodu X [vstup] se řídí kružnicemi, zatímco pro bod Y [výstup] jsou směrodatné odpovídající kosočtverečky. A k danému
kosočtverečku se s těmi sousedními kosočtverečky přiblížíte podstatně
rychleji než k odpovídající kružnici sousedními kružnicemi.
Druhá zajímavá vlastnost spočívá v tom, že Minkowského funkce zobrazuje všechny kvadratické iracionality (tedy kořeny kvadratické rovnice s ceočíselnými koeficienty) na racionální čísla. Ukážu vám malý příklad. Vezměme si kvadratickou rovnici
x² + 2x - 5 = 0
Jedno z jejích řešení je číslo -1+sqrt(6), tedy zhruba 1.44949... Toto je podle definice kvadratická iracionalita a Minkowského funkce ji také náležitě zobrazí na zlomek - v tomto případě 31/21 (výpočet ale není úplně snadný). A takhle je to pro každou kvadratickou iracionalitu (pár dalších příkladů je výše v textu, těsně před grafem). Neznám žádnou jinou spojitou funkci, která by tento malý matematický zázrak dokázala implementovat.
Když jsme probírali živočichozpyt číselné osy, přirovnal jsem racionální čísla ke kostře našeho číselného systému a kvadratické iracionality k jakési chrupavce. Minkowského funkce nám ukazuje proč - tento typ iracionality je se zlomky spojený velmi krátkou pupeční šňůrou.
Pro první vlastnost je Minkowského funkce cenná v teorii míry a integrálu (a také je to příklad funkce, která je spojitá, ale ne absolutně spojitá), pro tu druhou pak v teorii čísel.
Wikipedia: Cantor
function (devil's staircase)
Wikipedia:
Minkowski's function (slippery devil's staircase)
Článek je redakčně upravenou verzí blogového příspěvku na serveru
iDNES.cz. Publikováno s laskavým svolením autora.
Další díly a původní texty jsou dostupné na blogu Jana Řeháčka.




