Na číselné ose najdeme kromě jednotlivých čísel také velmi zajímavé množiny - jakési číselné komunity. K nejznámějším patří jedna stará fraktální struktura, tradičně nazývaná jako Cantorovo diskontinuum.
Stejně jako košile i podmnožiny číselné osy se na trh dodávají v nejrůznějších velikostech, které se dají různými způsoby poměřovat. Některé množiny jsou velké, protože mají hodně prvků a jiné svou velikost odvozují třeba od délky. A musíme dávat dobrý pozor, abychom tyto vlastnosti nezaměňovali.
To ostatně platí i pro košile. Jejich velikost je také možné měřit podle různých kritérií. Některé mají hodně čísel kolem krku a jiné zase delší rukávy. A všichni víme, že atributy „šířka kolem krku“ a „délka rukávu“ mají úplně jiný význam, přestože oba vyjadřují určitý typ velikosti. V principu jsou tyto míry nezávislé a z toho, že má někdo široký krk, ještě nemůžeme usuzovat, že bude mít také dlouhé ruce.
Pokud mluvíme o velikosti množin, musíme též dávat dobrý pozor, o kterém atributu je zrovna řeč. To, že má nějaká množina hodně prvků, ještě neznamená, že musí být „dlouhá“. Například jednotkový interval (0,1) má poměrně malou délku 1, ale přesto obsahuje nekonečně mnoho čísel, dokonce nespočetně mnoho. Vlastně se dá ukázat, že obsahuje stejně mnoho prvků jako celá číselná osa (jejíž délka je nekonečno).
Intermezzo: Jako rychlé opáčko si připomeňme, že interval je podmnožina číselné osy, která obsahuje všechna čísla „vocaď pocaď“ s tím, že pokud se krajové body do intervalu započítávají, říkáme mu uzavřený interval a značíme ho [a,b], zatímco v opačném případě (krajní body k intervalu nepatří) mluvíme o otevřeném intervalu a značíme jej (a,b). Zde jsem výrazy „vocaď pocaď“ nahradil písmenky a,b. Délka tohoto intervalu je (b-a) nezávisle na tom, zda je otevřený či uzavřený.
Extrémním případem množiny, která je velká co do počtu prvků, ale malá ve smyslu délky, je takzvané diskontinuum, jehož obecnou formu publikoval německý matematik George Cantor v roce 1883 (má se ovšem za to, že diskontinuum objevil už v roce 1874 H. J. S. Smith). Abychom se diskontinuu mohli podívat na zoubek, musíme nejdřív navázat na minulé Matykání a říci si, jak je možné běžná desetinná čísla zapsat v jiných číselných systémech.
Dnes budu používat stejné značení jako minule a ze střední školy ještě připomenu, že záporné mocniny jsou převrácené hodnoty mocnin kladných. Takže jako příklad: 2^(-3)=1/8, 2^(-2)=1/4, 2^(-1)=1/2, 2^(0)=1,... Koho to zajímá podrobněji, může se obrátit na tetičku Wikipedii nebo nejbližší učebnicí vyšší aritmetiky.
Číselné systémy (dokončení)
Zápis reálných (desetinných) čísel v jiných číselných systémech probíhá podobně, jako jsme to viděli minule u čísel přirozených. Opět bude nejlepší, když se na to budeme dívat jako na problém převodu peněz mezi dvěma různými systémy bankovek. Jedny jsou vyjádřené v mocninách desítky a druhé v mocninách zatím nespecifikovaného základu. Jediný rozdíl je, že tentokrát budeme používat i záporné mocniny, to znamená, že se setkáme také se zlomkovými hodnotami naší měny (můžete se na ně dívat jako na jakési „haléře“).
Jakmile se nám povede dané číslo zapsat pomocí záporných mocnin nového základu, koeficienty tohoto rozvoje nám opět ukáží, jak se zvolené číslo v daném systému zapíše. Jako příklad si zapíšeme číslo pí v trojkovém systému (tedy se základem 3). Protože s celými čísly jsme se vypořádali v minulém Matykání, bude stačit, když trojkově rozvineme jeho desetinnou část: 0.141592653...
Představme si tedy, že toto je částka, kterou chceme zaplatit, a k dispozici máme pouze trojkové „mince“ (tedy záporné mocniny základu 3), což jsou tato čísla:
3^(-1) = 1/3 = 0.3333333...
3^(-2) = 1/9 = 0.1111111...
3^(-3) = 1/27 = 0.0370370...
3^(-4) = 1/81 = 0.0123457... ...
Hned vidíme, že první mince (1/3) je na naši částku příliš vysoká, a tak platbu zahájíme druhou mincí (1/9). Po odečtení její hodnoty nám k doplacení zbývá 0.141592-0.111111, což je 0.030481. Opět vidíme, že následující mince (1/27) je příliš velká (její hodnota je větší než to, co máme doplatit), a tak sáhneme po další minci (1/81), která se nám do doplatku vejde hned dvakrát (ověřte si, že tři mince už by byly moc). Dvě mince (1/81) odečteme a zůstane nám k doplacení 0.030481 - 2*0.012345 = 0.005791... Takto pokračujeme stále dál. U reálných čísel si samozřejmě musíme vybrat, jak přesně číslo chceme zapsat, a podle toho se rozhodneme, kdy s rozvojem přestat. Zatím jsme pro necelou část pí dostali následující rozklad na trojkové mince (tedy záporné mocniny):
0.141592653... = 0*(1/3) + 1*(1/9) + 0*(1/27) + 2*(1/81) + ...
Koeficienty shrneme do konečného trojkového zápisu (0.0102...). Když k tomu ještě připočteme celou část, která se trojkově zapíše jako (10), dostaneme pro pí úhrnný trojkový zápis (10.0102...). Kdo se chce procvičit, může si zkusit vyjádřit pí v dalších systémech.
Obráceným směrem je to naštěstí jednodušší. Pokud nám někdo zadá číslo v nestandardním systému, například dvojkové x = (0.101101...), a poprosí o převedení do desetinného zápisu, tak si prostě uvědomíme, že číslo je vyjádřeno pomocí záporných mocnin dvojky, a bez okolků ho podle definice do mocnin rozepíšeme (a jsou to opět převrácené hodnoty mocnin kladných). Výše zadané dvojkové číslovky používáme jako koeficienty, takže
x = 1*(1/2) + 0*(1/4) + 1*(1/8) + 1*(1/16) + 0*(1/32) + 1*(1/64) + ...
a po vyčíslení na kalkulačce dostaneme zhruba 0.703125... Záměrně říkám „zhruba“, protože na přesnější vyjádření bychom potřebovali na vstupu podstatně delší dvojkový rozvoj.
+++
Nechme teď algebru algebrou a podívejme se, jak si můžeme čísla zapsaná v jiných systémech představit geometricky na číselné ose. A budu se dívat pouze na interval (0,1).
Nejprve si dobře prohlédneme, jak funguje desetinný systém (horní část obrázku v černém). Jednotkový interval rozdělíme na deset stejných podintervalů a lehce zjistíme, že v prvním interválku máme reálná čísla, jejichž první desetinná číslice (za desetinnou tečkou) je 0. Ve druhém jsou čísla, která mají bezprostředně za desetinnou tečkou jedničku, ve třetím dvojku a tak dále... až v posledním najdeme čísla, jejichž desetinný rozvoj začíná devítkou. A teď si každý z podinterválků můžeme opět rozdělit na deset chlívků a dostaneme dělení podle druhé desetinné číslice. Na obrázku jsem to udělal pro interval označený 0.3... Ten se rozpadne na deset malých chlívků s tím, že v prvním máme číslice s desetinným rozvojem typu 0.30... (tedy druhá desetinná číslice je nula - ta první je samozřejmě trojka), v druhém čísla, jejichž druhá desetinná číslice je jednička, a tak dále. Až v posledním máme čísla s rozvojem začínajícím na 0.39.. (to znamená, že druhá desetinná číslice je 9). A kdybychom jeden z malých chlívků zase rozdělili na deset dílků, tak bychom dostali dělení podle třetí desetinné číslice.
Pro ostatní číselné systémy se základem N je geometrická interpretace úplně stejná, jen základní interval nerozřežeme na deset, ale na N dílků, a k očíslování používáme pouze číslovky 0,1,... N-1. Žádné vyšší číslovky v těchto systémech nepotřebujeme.
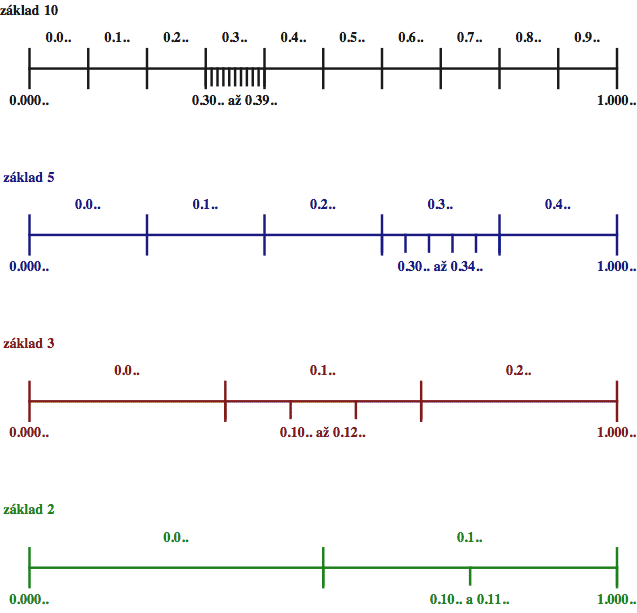
Podívejme se podrobněji třeba na základ 3. Interval (0,1) rozřežeme na
tři díly, přičemž v prvním máme čísla, jejichž trojkový zápis
začíná 0, ve druhém ta, která začínají jedničkou a ve třetím ta,
která začínají dvojkou. A teď jsem si vybral prostřední interval (tj.
čísla začínající trojkově výrazem 0.1...) a opět jsem ho rozřezal na
tři kousky. Tím jsem dostal tři podinterválky pro čísla, jejichž druhá
trojková číslice je postupně 0, 1 a 2 (jejich trojkové zápisy tedy
začínají na 0.10..., 0.11.. a 0.12). A stejně jsem to pochopitelně mohl
udělat i pro první interval (čísla, která mají první trojkovou číslici
rovnou nule). Kdybych ho rozřezal na tři stejné dílky, opět bych dostal
podintervaly odpovídající trojkovým zápisům začínajícím na 0.00..,
0.01.. a 0.02.. (tyto podintervaly by tedy obsahovaly čísla, jejichž první
trojková číslice je 0 a ta druhá je postupně 0, 1 a 2).
Zkrátka při prvním rozřezání dostaneme dělení podle první číslice daného zápisu, při druhém podle druhé, při třetím podle třetí atd. Takový geometrický pohled na věc je v mnoha případech užitečnější než aritmetické martyrium, které jsme podstoupili na začátku této sekce.
Cantorovo diskontinuum
A teď už k věci. Cantorovo diskontinuum je podmnožina číselné osy ležící v intervalu (0,1), která má spoustu zajímavých vlastností (např. neceločíselnou dimenzi), a proto se používá jako učební pomůcka při hlubším studiu číselné osy (tzv. reálná analýza) a také při studiu fraktálů. K její konstrukci je však třeba nekonečně mnoha kroků (iterací), takže matematici tuto množinu rádi používají k trápení studentstva, neboť je hned vidět, kdo se s nekonečnem opravdu kamarádí a kdo přátelský vztah jenom předstírá.
Prvních šest kroků obsahuje ilustrační obrázek níže. Začneme s jednotkovým intervalem (0,1). To je naše první iterace (řádka označená černou jedničkou). Ve druhé iteraci z tohoto intervalu vyjmeme prostřední třetinu a vyhodíme ji. Zbytek si ponecháme. Ve třetí iteraci dvě krajní třetiny opět rozřežeme na tři kousky, prostřední třetiny vyhodíme a zbytek si ponecháme. Dostaneme tak čtyři malé intervaly a pokračujeme dál. Ve čtvrté iteraci ze všech interválků na třetím řádku opět vyhodíme prostřední třetinu, a tím získáme osm pidiinterválků. A takto pokračujeme dál. To, co získáme po provedení nekonečně mnoha „vyhození“, je Cantorovo diskontinuum.
Rád bych zdůraznil, že to, co vidíme na každém řádku, je jen jakási stále se zlepšující aproximace Cantorovy množiny. Množinu samotnou si musíte představit v hlavě. Na žádném řádku s konečným pořadovým číslem ji neuvidíte. Ona leží až úplně dole v nekonečnu. To, co na pomyslném nekonečném řádku najdete, je jen „roztroušený prach“ – finální Cantorova množina (diskontinuum) neobsahuje žádný souvislý interval, ani ten nejmenší.
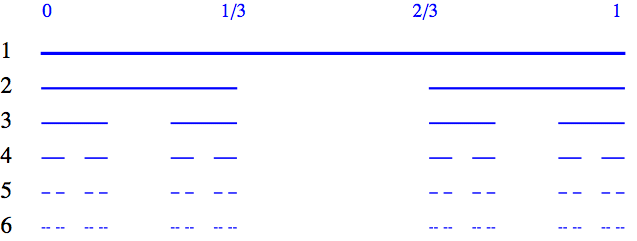
Docela dobrou představu o struktuře Cantorovy množiny si však můžeme
udělat pomocí trojkového zápisu z předchozí sekce. Jinými slovy, budeme
si všechna reálná čísla z intervalu (0,1) představovat zapsaná v trojkové soustavě. V prvním kroku (z iterace 1 do iterace 2) jsme vyhodili
prostřední třetinu, která přesně odpovídá číslům, jejichž první
trojková číslovka je 1. V dalším kroku jsme ze zbývajících třetin opět
vyhodili prostřední třetinu, a tím i všechna čísla, jejichž druhá
číslovka (v trojkové soustavě) je 1. Teď už je do toho celkem vidět. V každém kroku prostě z jednotkového intervalu vyhazujeme čísla, jejichž
další trojková číslovka je jednička. Iterativní postup tedy postupně
požírá čísla, jejichž trojkový zápis obsahuje někde jedničku. Nakonec
nám zůstanou čísla, jejichž trojkový zápis prostě žádnou jedničku
neobsahuje. Takových čísel je samozřejmě dost, například
(0.200202202222020002)... atd. Sami si lehce najdete spoustu dalších, a pokud
se nudíte, tak si je můžete převést do desetinného zápisu a graficky
zaznamenat na jednotkový interval.
+++
Když máme o Cantorově diskontinuu jakous takous představu, podíváme se na některé jeho vlastnosti.
Nejprve na délku. Snadno si spočítáme, kolik jsme toho vlastně celkem vyhodili. V prvním kroku jsme vyhodili jednu prostřední třetinu o délce 1/3. Ve druhém kroku jsme vyhodili dvě třetiny o délce 1/9, tedy suma sumárum jsme se zbavili 2/9. Ve třetím kroku (na řádku označeném 3) jsme měli čtyři intervaly (o délce 1/9) a z každého jsme vyhodili prostřední třetinu o délce 1/27, takže celkově jsme se v tomto kroku zbavili 4/27. A teď si to postupně sečteme:
vyhozeno = 1/3 + 2/9 + 4/27 + 8/81 + ...
a to není nic jiného než nekonečná geometrická řada s prvním členem a=1/3 a s koeficientem q=2/3. Její součet je tedy a/(1-q) a to je po dosazení přesně 1! Celková délka všech vyhozených intervalů je tedy 1, což byla současně i délka startovního intervalu. My jsme vyhodili prakticky všechno. Respektive délka toho, co jsme vyhodili, je stejná jako délka toho, s čím jsme začali. Na Cantorovo diskontinuum tak zbývá nula: 0 = 1 - 1. Technicky říkáme, že Cantorova množina má délku 0 (a nebo ještě techničtěji míru 0 – „míra“ je zobecněním pojmu „délka“).
Aby nevznikl dojem, že pokud se součet délek vyhozených intervalů rovná původní délce, tak nám nic nezbyde, uvažme toto. Vezměme si uzavřený interval [0,1] a vyhoďme z něho dva otevřené intervaly: (0,1/2) a (1/2,1). Délka počátečního intervalu je 1 a oba vyhozené intervaly mají délku 1/2. Přesto jsme nevyhodili úplně všechno. To, co nám v tomto případě zbyde, budou tři body: 0, 1/2 a 1. Moc toho sice není, ale je vidět, že alespoň něco málo nám v principu zbýt může.
A jak je to tedy se zbytkem v případě Cantorovy množiny. Zbyde nám toho na pomyslné poslední řadě hodně nebo málo?
Představit si finální množinu je opravdu těžké, ale na druhé straně víme zcela přesně, jaký je trojkový rozvoj čísel, které množina obsahuje - chybí v nich jednička! A to nám umožní ukázat, že čísel, která nám po vyhození všech prostředních třetin zbydou, je přesně tolik, kolik bylo čísel v původním intervalu (0,1). Zní to absurdně, ale je to tak. Tolik jsme toho vyházeli, a přesto nám toho tolik zbylo! Po vzoru Matykání o nekonečnu si sestavíme spárování tanečnic a tanečníků mezi Cantorovou množinou a původním intervalem (0,1). Každému tanečníkovi z původního intervalu najdeme tanečnici v Cantorově diskontinuu. A to spárování nenechá nikoho sedět v koutě. Ani Antonína.
Každé číslo z jednotkového intervalu (tanečník) má dvojkový zápis. Ten mávnutím kouzelného proutku proměníme tak, že všechny jedničky v rozvoji změníme na dvojky a výsledek interpretujeme jako číslo zapsané v trojkové soustavě. Co tím dostaneme? Prvek Cantorova diskontinua! Tedy tanečnici. Trojkový zápis totiž nebude obsahovat ani jednu jedničku.
Podívejme se na příklad. Vyberme si číslo z původního intervalu (0,1), jehož dvojkový zápis je třeba (0.1011010001...) Číslo teď mávnutím proutku proměníme v prvek Cantorovy množiny tím, že v něm všechny jedničky zcela mechanicky vyměníme za dvojky: (0.2022020002...) Vidíte v něm nějakou jedničku? Já ne. A tohle kouzlo zapůsobí úplně stejně na všechna čísla z původního intervalu zapsaná ve dvojkové soustavě. Ať si vyberete jakéhokoliv tanečníka, tímto kouzlem mu lehce najdete Cantorovskou tanečnici. A co je nejdůležitější, když si vyberete dva různé tanečníky, tak i Cantorovské tanečnice budou různé. Můžeme si kouzlo tedy skutečně představit jako spárování tanečníků a tanečnic.
A naopak můžeme každé tanečnici z Cantorovy množiny přiřadit jednoho tanečníka z původního intervalu tak, že vezmeme trojkový zápis čísla c, řekněme c=(0.22022202...), a změníme všechny dvojky na jedničky. Dostaneme nové číslo d=(0.11011101...) a to interpretujeme jako dvojkový rozvoj čísla mezi nulou a jedničkou. Díky tomu, že trojkové rozvoje Cantorovy množiny neobsahují jedničky, budou prvky obou množin opět přesně spárované (jako tanečníci a tanečnice) a to v matematice znamená, že obě množiny mají stejně mnoho prvků.
Pokud vám vrtá hlavou, k čemu je dobré, že cantorovské trojkové rozvoje neobsahují žádné jedničky, představte si, co by se stalo, kdyby se nám tam jedničky vloudily. Pak bychom mohli mít dvě různé cantorovské tanečnice c1=(0.2100222...) a c2=(0.2200222...). A když teď mávneme kouzelným proutkem a dvojky změníme na jedničky, zjistíme, že obě mají stejného tanečníka: (0.1100111...) A to by byl problém!
Ale zpátky k tématu. Z původního intervalu (0,1) jsme sice skoro všechno vyhodili (ve smyslu délky), ale nakonec nám zůstalo dost bodíků, abychom je mohli spárovat s body původního intervalu.
Tím jsme ukázali, že Cantorova množina (diskontinuum) má i po těch šílených vyhazovacích orgiích stejně mnoho prvků jako původní interval. Je tedy stále nespočetná, přestože jsme zdánlivě všechno podstatné z intervalu odstranili. Je to jako kouzelnický trik – vezmete si všechny body mezi nulou a jedničkou, trochu je přerovnáte a – simsalabim – jejich délka je najednou nula. Laik žasne a odborník se diví.
Řečeno nevědecky: představte si, že děláte úklid. Prakticky všechno z baráku vyházíte, a pak zjistíte, že vám v něm prakticky všechno zůstalo. No není ta matematika na palici?
Článek je redakčně upravenou verzí blogového příspěvku na serveru
iDNES.cz. Publikováno s laskavým svolením autora.
Další díly a původní texty jsou dostupné na blogu Jana Řeháčka.