Dnes si uděláme malý výlet do říše hudby. Ale úplně bezbolestné to nebude. Abychom si mohli odpovědět na titulní otázku, musíme se naučit, jak aproximovat iracionální čísla pomocí zlomků.
V okamžiku, kdy lidstvo zjistilo, že zdaleka ne všechna čísla jsou racionální – a to bylo ještě za starého Řecka – vyvstala přirozená otázka, jak by se iracionální čísla dala pomocí racionálních alespoň aproximovat. Tedy jak by se daly najít zlomky, jejichž numerická hodnota by se od daného iracionálního čísla příliš nelišila. Zlomky jsou sice na číselné ose poměrně vzácné (je jich pouze spočetně mnoho), ale jsou konceptuálně mnohem jednodušší než iracionální čísla – dá se s nimi rozumně počítat, a proto jsou na číselné ose vyhledávanou náhražkou všech těch tajuplných monster s nekonečným desetinným rozvojem.
Je to tak trochu, jako když režisér hledá kaskadéra pro nějakou nebezpečnou scénu. Kaskadér musí jednak vypadat jako hlavní hrdina a jednak to musí být speciálně vycvičený, tvrdý chlap. S racionálními aproximacemi je to podobné. Zlomky jsou matematičtí kaskadéři, příslušníci speciálně vycvičené algebraické jednotky rychlého zásahu, kteří občas za své poněkud neohrabané iracionální kolegy zaskakují při natáčení komplikovaných aritmetických scén. Ovšem musejí vypadat podobně – tedy nesmějí se od nich numericky příliš lišit.
Pokud se náhodného školáka zeptáte, jaká je hodnota čísla pí, skoro určitě vám odpoví 3,14. To samozřejmě není přesná hodnota (ta by se nám na papír nevešla), nýbrž pouze přibližná. V podstatě se na ni můžeme dívat jako na racionální aproximaci, protože číslo 3,14 se dá – jako každé konečné desetinné číslo – zapsat jako zlomek: zde 314/100 (a po zkrácení 157/50). Toto je jedna z možností, jak iracionální čísla pomocí zlomků aproximovat. Má však jednu chybičku.
Všechny aproximace, které bychom tímto „triviálním“ způsobem dostali, budou mít ve jmenovateli mocninu desítky. Tak třeba číslo e = 2,718... by se jistě dalo napsat jako 2718/1000, ale asi cítíte, že tímto postupem si zbytečně omezujeme pole možných kandidátů. Asi tak, jako kdyby firma potřebující novou účetní hledala pouze mezi uchazečkami, které nosí fialové lodičky.
Je přece spousta zlomků, které ve jmenovateli mocninu 10 nemají, a přesto mohou být dobrými aproximacemi nějakého iracionálního čísla. Například již staří Egypťané věděli, že naše magické číslo pí se dá napsat zhruba jako 22/7 (což je v desetinném přepočtu přibližně 3,14286...). A právě o těchto „netriviálních“ aproximacích je dnešní Matykání.
Jak najít kvalitní aproximace iracionálních čísel
Výše popsaný, „školácký“ způsob hledání racionálních aproximací je sice trochu naivní, ale dá nám dobré vodítko pro solidnější postup. Proto si ho zopakujeme. Vezmeme si iracionální číslo, třeba to staré dobré 3,141592653..., pak ho někde usekneme – řekněme, že vezmeme 3,14 – a nakonec tento „pahýlek“ převedeme na zlomek 314/100. Samozřejmě, pokud bychom chtěli přesnější aproximaci, tak číslo prostě „usekneme“ o kousek dál, řekněme 3,14159, a dostaneme aproximaci 314159/100000.
Pokud však chceme zlomky, které budou mít ve jmenovateli něco jiného než mocninu 10, budeme se muset oprostit od desetinného zápisu. V minulém Matykání jsme se naučili zapisovat reálná čísla rozvojem do řetězového zlomku, který nepředpokládá žádný pevný základ (ať už 10 nebo nějaký jiný). Nabízí se tedy otázka, zda bychom kvalitní zlomkové aproximace nedostali tak, že nekonečný řetězový rozvoj iracionálního čísla někde usekneme a ten „pahýlek“ pak rozvineme do normálního zlomku (to jsme se naučili minule). A tak to skutečně funguje. Dokonce lze ukázat, že takové aproximace jsou v jistém smyslu nejlepší možné. A stejně jako v desetinném případě bude platit, že čím delší „pahýlek", tím přesnější aproximace.
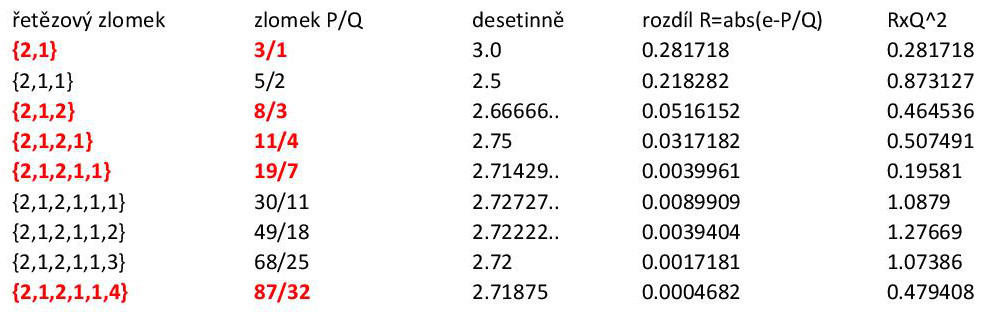
Tady je příklad. Minule jsme viděli, že Ludolfovo číslo má řetězový rozvoj {3;7,15,1,292,1,1,...}. Vezměme si tedy pro začátek první dva členy {3;7}, což v normálním přepisu znamená 3 + 1/7, a to nám dá 22/7. Objevili jsme tedy aproximaci starých Egypťanů. Teď si vezmeme první tři: {3;7,15}. Tady už je vyčíslení komplikovanější, ale když si ho uděláte za domácí úkol, dostanete 333/106, což je 3,14151 (to už je velice solidní aproximace). Další „pahýlek“ na řadě je {3;7,15,1}, odpovídající (po vyčíslení řetězového zlomku) poněkud mysterióznímu výrazu 355/113, který si možná pamatujete ze školy. Učitelé ho rádi citují, protože jej dostanete tak, že napíšete tři páry lichých čísel 113355, roztrhnete je na dvě poloviny a jednu šoupnete do čitatele a druhou do jmenovatele. Desetinná hodnota tohoto zlomku je 3.14159292... Všimněte si, že tento zlomek už uhodl 6 čísel, přestože jeho jmenovatel je stále jen zhruba stovka (!). A nakonec si dáme „pahýlek“ z prvních pěti členů řetězového zlomku {3;7,15,1,292} a ten opět rozvineme ve zlomek normální: 103993/33102. Jeho desetinná hodnota je 3,141592653012... Tady už máme v richtiku 9 čísel, což je víc než by průměrný inženýr mohl kdy potřebovat. Kdybyste si takovou aproximaci chtěli napískat tím „školáckým“ (desetinným) způsobem, museli byste mít jmenovatel v řádu miliard (nám tady stačí jen něco přes 33 tisíc).
Zlomkům, které jsme z useknutých pahýlků dostali, se říká konvergenty. Takže konvergent odpovídající řetězovému zlomku {3;7} je 22/7. Někdy se pro aproximaci používají i tzv. semikonvergenty, kde poslední řetězový člen postupně zmenšujete – v tomto případě bychom dostali následující semikonvergenty: {3;6} = 19/6, {3;5} = 16/5 atd. Tyto zlomky však obvykle neposkytují tak kvalitní aproximace.
Abychom si to procvičili, sestrojíme si tabulku konvergentů (červeně) i semikonvergentů pro číslo e (2,71828...), jehož řetězový rozvoj je {2;1,2,1,1,4,1,1,6,...}. V předposlední sloupci vám ukážu absolutní hodnotu rozdílu mezi aproximovaným číslem e a jeho racionální náhražkou P/Q. V posledním sloupci tento rozdíl ještě vynásobím čtvercem jmenovatele, což je v teorii aproximace standardní způsob, jak měřit kvalitu dané aproximace (v sekci Jauvajs níže se podíváme, proč tomu tak je).
Minule jsme viděli, že konečný řetězový zlomek nám ukazuje, jak se
pohybovat po Stern-Brocotově stromu, abychom se dostali do zvoleného zlomku.
Pro iracionální čísla (s nekonečným řetězovým zlomkem) to platí
podobně, jen s tím rozdílem, že naše cesta stromem nikdy nekončí a zlomky, které při cestě míjíme, jsou nejlepší možné racionální
aproximace našeho iracionálního čísla.
Jak ladit hudební nástroje
Podle staré legendy si Pythagoras jednou u kováře povšiml, že kladiva, kterými tento buší do perlíku, vyvolávala v jistých případech akusticky libé vjemy. Kladiva vážila 12, 9, 8 a 6 liber a jejich simultánní údery vyluzovaly zvuky, jejichž kmitočty byly v poměru 12:6 = 2:1 (oktáva), 12:8 = 3:2 (čistá kvinta) a 12:9 = 4:3 (čistá kvarta). K těmto základním poměrům se v průběhu historie přidaly ještě další intervaly: 9:8 (velká sekunda, tedy celý tón), 6:5 (malá tercie), 5:4 (velká tercie), 8:5 (malá sexta) a 5:3 (velká sexta). Tady bych ještě zdůraznil, že pro pocit konsonance je důležitý poměr kmitočtů, nikoliv jejich absolutní hodnota. Však se také o tom, zda má komorní áčko být 440 Hz, a nebo 435 Hz, poměrně dlouho vedly spory.
Hudba tedy v jistém smyslu není nic jiného než počítání se zlomky (kvintový poměr 3:2 je jen jiný zápis zlomku 3/2). Například pokud postavíme dva intervaly na sebe, nový kmitočtový poměr vznikne vynásobením těch výchozích. Zahrajeme-li kvintu (C1-G1) a pak kvartu (G1-C2), dostaneme nový podíl frekvencí z jejich výše uvedených poměrů: (3/2) * (4/3) = (2/1), což je přesně oktáva (C1-C2), kterou očekáváme. Zahrajeme-li tón o oktávu vyšší, jeho kmitočet zdvojnásobíme (pokud je tón o oktávu nižší, jeho kmitočet naopak vydělíme 2).
Ještě jeden příklad, abychom to dostali do krve. Postavíme dvě kvinty na sebe (C1-G1-D2) a dostaneme poměr (3/2) * (3/2) = (9/4). To déčko je ovšem o oktávu výš, takže ho stáhneme dolů oktávovým poměrem (1/2) a dostaneme (9/4) * (1/2) = (9/8). To je přesně výše citovaný poměr pro celý tón (9:8).
Abych mohl umocňovat, budu pro mocninu používat symbol ^, takže 2^3 znamená „dvě na třetí“ a místo (3/2) * (3/2) bych teď mohl napsat (3/2)^2 (tři poloviny na druhou). Asi jste také zaznamenali, že pro „krát“ používám symbol * .
Zdálo by se tedy, že v hudbě je vše v nejlepším pořádku a nic nám nebrání naladit si nástroje a pustit se do muzicírování. Jenže matička matematika nám ošklivě hrábne do strun. Pojďme si zkusit velkou tercii C-E (ta by měla odpovídat poměru 5:4). Vezmeme si tedy čtyři na sebe nakupené kvinty (C1-G1-D2-A2-E3), které odpovídají poměru (3/2)^4 = 81/16. Snížíme ho o tři oktávy (2^3 = 8), abychom to éčko dostali zpět do původního intervalu, a dostaneme: (81/16) * (1/8) = (81/64). A najednou jsme v háji. Tohle není 5/4. Tenhle zlomek má hodnotu 1,26563, zatímco naše milá tercie by měla být (5/4) = 1,25 (!). Neudělali jsme někde chybu? Neudělali. Hudba v sobě skutečně ukrývá záludnou past.
Z pozice teorie čísel past spočívá v tom, že zlomek pro tercii v sobě obsahuje pětku a tu si z dvojek a trojek (ze kterých se skládají poměry pro kvartu, kvintu i oktávu) nenabrnkáme, ani kdybychom se na hlavu postavili.
Abychom do věci vnesli trochu systematičnosti, uvědomíme si, že nestačí jenom kvinty neustále vršit na sebe (a produkovat nové a nové tóny), ale v jistém okamžiku bychom se rádi dopracovali zpátky k základnímu tónu, tedy k céčku (byť zvýšenému o příslušný počet oktáv). To znamená, že určitý počet kvint by měl korespondovat nějakému jinému, ale zcela konkrétnímu počtu oktáv. Jenže kmitočtové poměry oktáv odpovídají mocninám dvojky: (2, 4, 8, 16...), zatímco na sebe navršené kvinty budou odpovídat mocninám zlomku (3/2), což je 1,5, a tyto dvě řady se nikdy nesrovnají (mocniny tří polovin nikdy nebudou celočíselné, natož aby byly mocninami dvojky).
V tom spočívá velké dilema hudby. Nástroje se prakticky nedají naladit tak, aby v nich všechny intervaly zněly čistě (tedy aby jejich kmitočty odpovídaly výše uvedeným poměrům). A když říkám „nedají“, tak tím myslím, že je to skutečně matematicky nemožné. Budeme tedy muset slevit a pokusit se najít nějaký přijatelný kompromis.
Tady je výpočet (aspirin do pohotovostní polohy).
Naším cílem je, aby se po zahrání Q kvint ozval stejný tón jako po zahrání P oktáv, kde P a Q jsou dvě celá čísla, která se za okamžik pokusíme spočítat. Vzhledem k tomu, co jsme si řekli o skládání intervalů, je jasné, že tato dvě čísla musí splňovat následující rovnici (pravá strana počítá oktávy, levá kvinty):
(3/2)^Q = (2/1)^P
Teď z pravé i levé strany vezmeme Q-tou odmocninu (tedy umocníme na 1/Q):
(3/2)= 2 ^ (P/Q)
Nakonec na obě strany aplikujeme přirozený logaritmus
ln(3/2) = (P/Q) * ln(2)
s tím, že tuto rovnost vydělením upravíme do tvaru
P/Q = ln(3/2)/ln(2) = ln(1,5)/ln(2).
A jsme doma. Tahle rovnice se nedá vyřešit (jak se dalo čekat). Číslo napravo je totiž iracionální, zatímco nalevo máme evidentní zlomek (stále předpokládáme, že P a Q jsou celá čísla). Co teď s tím?
Nejlepší, co v této chvíli můžeme udělat, je aproximovat číslo napravo zlomkem a jeho čitatele a jmenovatele pak vzít za hodnotu P a Q. Tak s chutí do toho.
Iracionální číslo napravo má desetinnou hodnotu 0,584962500721.. a jeho řetězový rozvoj je {0, 1, 1, 2, 2, 3, 1, 5, 2...}. A můžeme začít aproximovat. První smysluplné useknutí {0, 1, 1, 2} nám dá 3/5 = 0,6 a to není bůhvíjak přesná aproximace výše uvedeného čísla (navíc by v tomto případě připadlo Q = 5 kvint na P = 3 oktávy a taková hudba by byla dosti chudá – měla by jen 5 tónů odpovídajících 5 kvintám). Takže usekneme „řetězák“ o jedno číslo dál: {0, 1, 1, 2, 2} a opět převedeme na normální zlomek: P/Q = 7/12 = 0,58333... To už je aproximace velmi dobrá a počet různých tónů (12) je tak akorát. Takže 12 kvint budiž rovno 7 oktávám. Věční šťouralové by ještě mohli zkusit další konvergent {0, 1, 1, 2, 2, 3}, který by nám dal řešení P/Q = 24/41 = 0,58536. To by sice bylo ještě o chlup přesnější, ale oktáva s 41 různými tóny (ve které by 41 kvint odpovídalo 24 oktávám) by nás asi přiváděla k zoufalství. Zlomek 7/12 je rozumným kompromisem mezi přesností a praktičností.
Pro většinu hudebníků budou výše uvedené rovnice asi zbytečně abstraktní (muzikanti mají raději rytmy než logaritmy). Aby tedy bylo jasnější, proč se zrovna 12 kvint blíží 7 oktávám, uděláme si zcela konkrétní tabulku všech kvint. Hned bude jasné, kde je zakopaný pes (zde mám na mysli domácí zvíře, nikoliv snížený tón pé).
V prvním sloupci uvedu tón, ve druhém budu počítat kvinty, ve třetím zapíšu příslušný kmitočtový poměr (tj. mocninu základního zlomku 3/2) a ve čtvrtém jeho desetinnou podobu. V předposledním sloupci vám ukážu nejbližší mocninu dvojky, která, jak už víme, reprezentuje kmitočtový poměr oktáv. Abychom viděli, jak daleko je daná kvinta od nejbližší oktávy, v závěrečném sloupci zaznamenám poměr posledních dvou čísel. Čím je tento poměr bližší jedničce, tím jsou si obě kvantity podobnější (a my chceme, aby si byly co nejpodobnější, když už stejné být nemohou). Na posledním řádku se můžete sami přesvědčit, jak jsme se u dvanácté kvinty „téměř“ trefili do mocniny dvojky (tedy do oktávy).
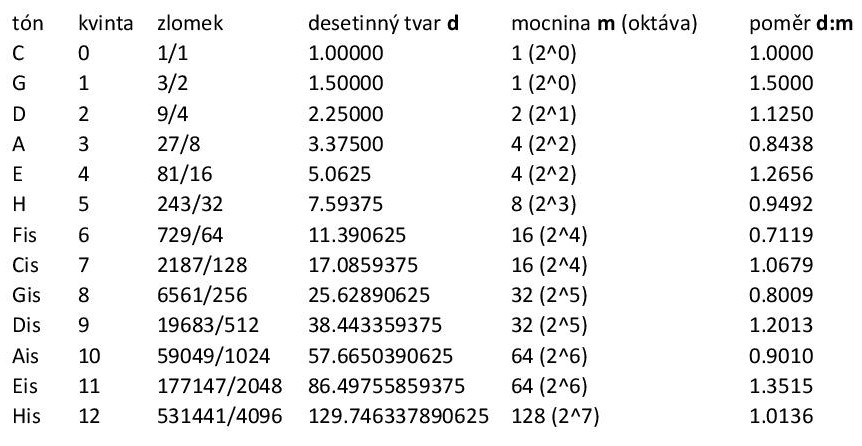
Na řádku Cis vidíte, že ani poměr 1.0679 by nebyl tak úplně k zahození. Ten by odpovídal situaci, kdy by se 7 kvint přibližně rovnalo 4
oktávám. Tohle řešení bychom dostali pomocí semikonvergentu {0, 1, 1, 2,
1}, který se rovná 4/7.
Poslednímu poměru (1.01364), který ještě musíme nějak zakamuflovat, se říká Pythagorejské koma. To vlastně není nic jiného než podíl kmitočtů 12 kvint a 7 oktáv, který by v ideálním světě byl roven 1.000. Jak ho zakamuflujeme (tedy přesněji, jak z těch 129.74 uděláme kýžených 128), záleží na tom, jaký typ ladění si vybereme. A to už je výzva ne pro matematiky, ale pro hudebníky. Různých ladicích systémů existuje celá řada, ale když to trochu zjednoduším, tak se můžeme omezit jen na dva základní:
1. Problém budeme až do poslední chvíle zatloukat, to znamená, že prvních 11 kvint (až po Eis) naladíme čistě – tedy tak, jak nám tabulka ukazuje – a na tu poslední pak necháme to, co „zbyde“ – tedy místo abychom His naladili na poměr 129.74, tak ho drze skrouhneme na 128, a dostaneme tak požadované céčko (posunuté o 7 oktáv). Tím však bohužel v našem hudebním nástroji vytvoříme příšerně znějící intervaly, kterým se celkem příznačně říká vlčí intervaly, protože skutečně znějí, jako když vyjí vlci. Takovému způsobu ladění se říká „pythagorejské“.
2. Druhou možností je nesrovnalost rozdělit rovnoměrně mezi všech 12 kvint. Žádná z nich potom nebude čistá, ale rozdíl bude tak malý, že ho většina neškolených uší vůbec nepostřehne. Rozdělíme tedy oktávu na dvanáct stejných půltónů s kmitočtovým poměrem p a pro jeho hodnotu dostaneme rovnici p^12 = 2 (12 stejných půltónů p nám musí dát oktávu, tedy dvojnásobný kmitočet), což znamená, že p = 2^(1/12) = 1.05946. Kvinta to však pochopitelně odskáče – bude mít 7 takových půltónů, takže její hodnota bude p^7 = 1.49831 a to je o fous méně než její čistá verze s kmitočtovým poměrem 1.500 (3/2). Tomuto ladění se říká „rovnoměrně temperované“ a dnes v drtivé míře převládá.
Mimochodem, staří Řekové si s těmito problémy hlavu příliš nelámali, protože v hudbě používali prakticky výlučně kvarty, kvinty a oktávy. Teprve když se v průběhu staletí začaly do hudby dostávat i tercie a sexty (např. prostřednictvím lidových písní), tak se ladění nástrojů muselo začít nějak slaďovat.
Sekce jauvajs: Jak posoudit kvalitu aproximace
pouze pro opravdu otrlé jedince
Když aproximujeme nějaké iracionální číslo zlomkem, je dobré mít kritérium, které nám řekne, zda je daná aproximace dobrá. Jinak by si totiž nějaký chytrák mohl vzít třeba zlomek 8/3 (což je zhruba 2,6666...) a tvrdit o něm, že je to dobrá aproximace čísla pí. On ten zlomek zase od „píčka“ tak daleko není.
Naivně by se to dalo udělat tak, že se podíváme, jaký je rozdíl mezi daným iracionálním číslem a jeho racionální aproximací, s tím, že budeme požadovat, aby tento rozdíl byl co nejmenší. To není špatná myšlenka, ale nedokáže rozlišit mezi zlomky s malým a velkým jmenovatelem.
Vezměme si třeba iracionální číslo pí a jeho aproximace 22/7 (3,14286) a 314/100 (3,14). Na první pohled jsou obě stejně kvalitní, protože „uhádly“ dvě desetinná místa, což znamená, že rozdíl mezi přesnou a aproximovanou hodnotou bude řádově 0,01. Ta první je však o něco „chytřejší", protože docílit stejné přesnosti s menším jmenovatelem je „cennější“. S velkým jmenovatelem to s prominutím zvládne každý blbec.
Obecně říkáme, že aproximace p/q iracionálního čísla x je nejlepší možná, pokud se žádný jiný zlomek se stejným (nebo menším) jmenovatelem k číslu x nedokáže přiblížit více. To je většinou formalizováno tak, že hledáme zlomky, u nichž bude malá nejen absolutní hodnota rozdílu (formulka vlevo), ale také jeho hodnota, když ji pronásobíme jmenovatelem na druhou (formulka vpravo). To nám umožní penalizovat zlomky, které mají zbytečně velký jmenovatel.
| x - p/q | versus q^2 | x - p/q |
Jako příklad, jak formulka vpravo funguje, si vezměme dvě aproximace pí uvedené na začátku této sekce: 314/100 a 22/7. První má následující chybu (v absolutní hodnotě): ch = | pí - 314/100 | = 0,00159265. Když ji vynásobíme jmenovatelem na druhou, dostaneme 100^2 ch = 15,9265. To je poměrně vysoká hodnota. A teď druhý zlomek. Chyba bude rovna: ch = | pí - 22/7 | = 0,00126449. Je tedy zhruba stejně velká jako ta předchozí. Jenže teď ji budeme násobit podstatně menším jmenovatelem na druhou a dostaneme 7^2 ch = 0,06196. Takto nám formulka vpravo napoví, zda jsme pro aproximaci nepoužili zbytečně velký jmenovatel. Tam, kde je výsledná hodnota větší než jedna, je aproximace většinou špatná (dobře to vidíte třeba na semikonvergentech pro číslo e v první tabulce).
Tady byste se mohli zarazit a zeptat se, proč rozdíl násobíme čtvercem jmenovatele, a ne jen jmenovatelem jako takovým. Ono totiž není na první pohled jasné, zda vůbec existují nějaké zlomky, pro které nám taková dryáčnická formulka dá rozumně malé číslo. Naštěstí analýzou Fordových kružnic (viz předminulé Matykání) zjistíme, že pro každé iracionální číslo x se zlomků p/q, které v tomto smyslu poskytují dobrou aproximaci, dá najít nekonečně mnoho (odpovídají konvergentům řetězového rozvoje).
Modrá čára na obrázku níže odpovídá iracionálnímu číslu x a jako taková protíná nekonečně mnoho Fordových kružnic (ty se ovšem rychle zmenšují, takže ty, co leží těsně nad osou x, si musíte představit – na obrázku nejsou vidět).
Kružnice odpovídající zlomku p/q má poloměr 1/2q^2. Pro každý takový zlomek tedy platí | x-p/q | < 1/2q^2. A když tuto rovnici pronásobíme q^2, zjistíme, že naše „pravá formulka“ nám dá číslo menší než 1/2, což nám pro dobrou aproximaci stačí.
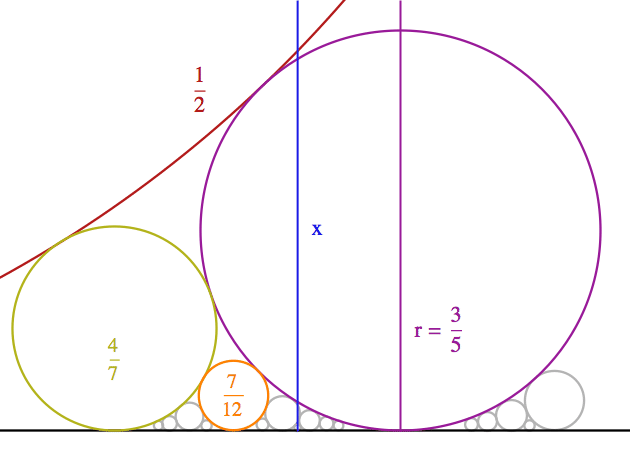
A ještě malá zajímavost. Při aproximaci nějakého racionální čísla
r (na obrázku vyznačeno fialově), se čára s nekonečně
mnoha Fordovými kružnicemi neprotne (protože kružnice odpovídající
číslu r je drží v bezpečném odstupu). To nás vede k paradoxnímu závěru, že racionální čísla se nedají ostatními
racionálními čísly aproximovat tak dobře jako čísla iracionální. To
sice zní na první pohled absurdně, ale je to tak a právě tato vlastnost
nám velice často pomáhá dokázat, že nějaké číslo není
racionální.
Když například v roce 1979 francouzský matematik Apéry šokoval matematický svět svým důkazem iracionality čísla Zeta(3), použil právě tuto vlastnost. Apéry ukázal, že Zeta(3) se dá velice dobře aproximovat racionálními čísly, a tudíž samo o sobě racionální být nemůže.
Článek je redakčně upravenou verzí blogového příspěvku na serveru
iDNES.cz. Publikováno s laskavým svolením autora.
Další díly a původní texty jsou dostupné na blogu Jana Řeháčka.




