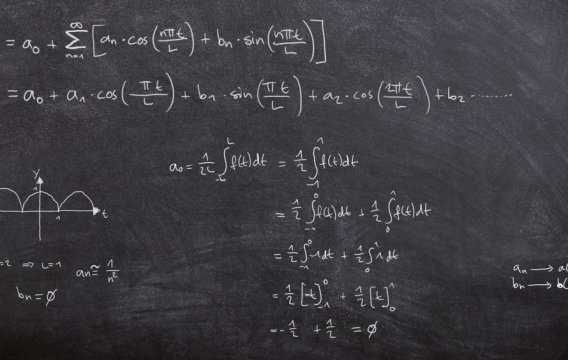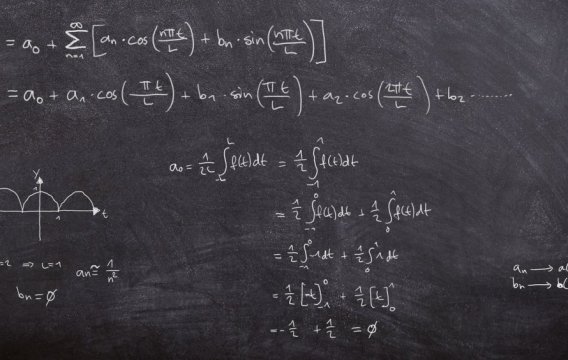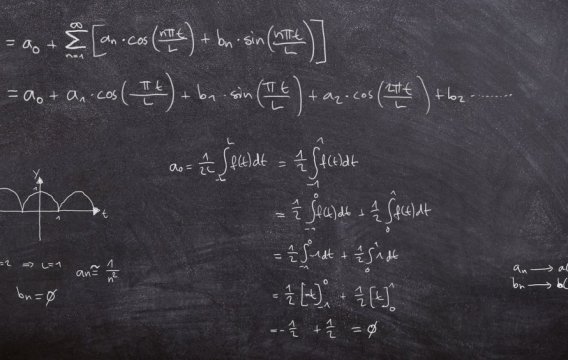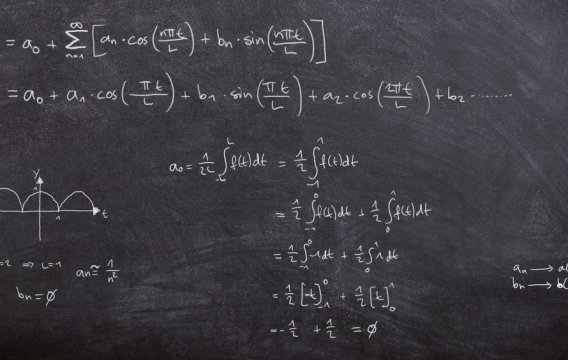Dnes budeme pokračovat ve zkoumání Stern-Brocotova stromu. A aby nám to šlo lépe od ruky, vypůjčíme si na to jednu archaickou matematickou vychytávku, kterou už v dnešních učebnicích moc nenajdete – řetězové zlomky.
Vesmír je plný potenciálně obyvatelných planetárních systémů a docela bych se divil, kdyby alespoň v některých nesídlily bytosti ženského pohlaví. Zda si je představujete jako Ginu Lollobrigidu v letech největší slávy, a nebo jako éterickou vílu s fialovými vlasy, trojitým poprsím a slušivými tykadly, která svým sourozencům po večerech trpělivě štupuje chitinový krunýř, je čistě věcí vaší fantazie. Máte-li však zájem o vesmírný románek, musíte na sebe nejprve dotyčnou nějak upozornit – nejlépe celoplošným vysláním výrazného optického signálu, protože nelze předpokládat, že v galaxii Andromeda mají všechny šťabajzny přístup na internet. To však neznamená, že můžete popadnout baterku, obrátit ji k noční obloze a jen tak mýrnix týrnix začít blikat. Při vysílání signálu je nutno dodržovat určité zásady.
V první řadě musíme dát milostivé dámě na srozuměnou, že nejsme žádný nazelenalý rosol přicuclý na otřískaném asteroidu IV. cenové skupiny, ale upravená, vzdělaná a citlivá bytost na bázi uhlíku s multifunkčními senzory a vlastním biovytápěním. Na svoji rozumovou vyspělost pak nejlépe upozorníme tím, že do optického signálu zakódujeme nějaké známé číslo, které musí všichni pracující inteligenti ve vesmíru znát. A tím nemám na mysli číslo vaší občanky nebo momentální počet obyvatel Bangladéše. Taková čísla jsou mimo rámec sluneční soustavy zcela nezajímavá. Ani rychlost světla ve vakuu se pro naše účely příliš nehodí, protože její numerická hodnota závisí na našich pozemských jednotkách. Nejlépe svou švarnou „Marťanku“ oslníme nějakou univerzálně srozumitelnou matematickou konstantou, například číslem pí (3,141592653589).
Ovšem pozor – při vysílání certifikátu o naší inteligenci bychom se měli vyvarovat desetinného rozvoje, protože a priori nevíme, kolik má naše vyvolená prstů, a tedy jaký základ pro svou číselnou soustavu používá. To, že zrovna my tady na Zemi máme deset prstů, v okolí Mléčné dráhy nikoho nezajímá. A naši vysněnou samičku teprve ne.
Každý muž ví, že jedná-li se ženou, nesmí ji spoutat vlastními konvencemi, ale musí se naopak podřídit konvencím jejím. Vyslat do vesmíru číslo pí v desetinném hávu by bylo jako pozvat slečnu na první rande v neděli na fotbal. Ne, pánové, ženy v naší části všehomíra mají rády, když se hraje podle jejich notiček. A my se přece chceme předvést jako sofistikovaný organismus, a ne nějaký intergalaktický balík, kterému čouhá desetinná čárka z bot.
Kdybychom například věděli, že slečna Yoothix ze systému Betelgeuze má na ruce čtyři prsty, tak bychom samozřejmě to píčko mohli příslušně přeformátovat ze soustavy dekadické (základ 10) do soustavy oktální (základ 8) – v ní by mimochodem Ludolfovo číslo vypadalo takto: 3.11037 55242... A my bychom na oplátku nevypadali jako dekadentní dekadik ze sluneční soustavy.
Jenže my nevíme, kolik má slečna Yoothix prstů, takže není zcela jasné, jakou soustavu vlastně zvolit (dekadickou, oktální, binární, hexadecimální nebo nějakou úplně jinou?). A protože na první pokus jistě nechceme budit dojem antropocentrického šovinisty zahleděného do vlastní desítkové soustavy, nabízí se otázka, zda by se číslo pí – a potažmo jakékoliv jiné číslo – nedalo vyjádřit (a odvysílat) nějakým univerzálním zápisem, který nepředpokládá žádný pevný základ. Jinými slovy zápisem, který není odvozen z konkrétního počtu prstů odesílatele. A jak jistě čekáte, takový zápis skutečně existuje. Říká se mu řetězový zlomek (anglicky continued fraction).
Tak s chutí do toho, ať slečna Yoothix nemusí moc dlouho čekat.
Řetězové zlomky
(pro jednoduchost budu v této sekci uvažovat pouze kladná čísla)
Řetězové zlomky jsou zlomky, které jsou do sebe vložené tak, že trochu připomínají ruské matrjošky. Tady jsou dva příklady (viz pravá strana níže uvedených rovnic).
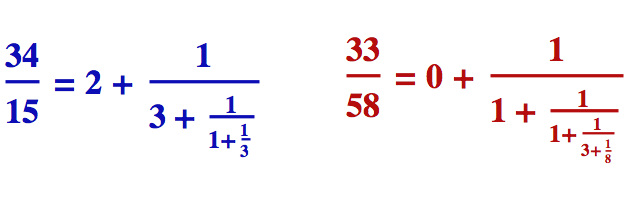
Nejprve si všimneme, že oba řetězové zlomky napravo mají v čitatelích jedničku. To je pro standardní řetězový zlomek charakteristické. Jejich hodnota je tedy plně určena posloupností jejich jmenovatelů (těm se někdy říká „členy řetězového zlomku“). A protože jsou řetězové zlomky z typografického hlediska taková celkem neohrabaná monstra, používá se pro jejich zkrácený zápis právě posloupnost jmenovatelů – většinou uzavřená v hranatých závorkách. Modrý zlomek napravo se zjednodušeně zapíše jako [2;3,1,3] a červený zase jako [0;1,1,3,8]. Všimněte si, že první číslo je oddělené středníkem, protože nám de facto ukazuje celou část daného zlomku.
Pokud chceme řetězový zlomek (pravá strana) vyčíslit a dopídit se jeho normální podoby (levá strana), stačí nám pouze opakovaně aplikovat pravidla o počítání se složenými zlomky – a začínáme vždy vpravo dole. Tak třeba modrý zlomek má (po vyčíslení) v pravém dolním rohu hodnotu 4/3 – to je vidět na první pohled. Když je převrátíte, dostanete 3/4, takže pod hlavní zlomkovou čárou vlastně máte 3 + 3/4, což je 15/4. Ty opět převrátíte (protože je tam jedna lomeno...) a dostanete 4/15, takže celková hodnota zlomku je 2 + 4/15 a to je těch kýžených 34/15.
O něco komplikovanější je to obráceně, tedy když vám někdo zadá normální zlomek a vy z něj musíte vyrobit ten řetězový. To se udělá postupným opakováním dvou (poměrně jednoduchých) operací:
1. ukousneme celou část
2. zbytek hodíme do sklepa
A teď podrobněji.
1. Ukousnutí celé části není nic jiného než vyjádření
zlomku v tzv. smíšeném tvaru. Třeba 9/4 = 2 + 1/4 a nebo 35/9 = 3 + 8/9
(pozor, někteří autoři to spojovací + vynechávají). Zkrátka z toho
zlomku oddělíme maximální možnou celou část.
2. Hození zbytku do sklepa je o něco rafinovanější a opírá se o známou poučku, že převrácená
hodnota převrácené hodnoty je původní číslo. Algebraicky to můžeme
vyjádřit takto: x = 1/(1/x). Tomu budu říkat sklepní rovnice.
Takže ten zbytek (po odečtení celé části) strčíme pod zlomkovou čáru,
ale musíme jeho hodnotu převrátit. To nám umožňuje jakýkoliv zlomek
menší než jedna převést na zlomek, který je větší než jedna.
Příklad: 3/5 = 1/(5/3). Všimněte si, že 3/5 jsou menší než jedna,
zatímco 5/3, které se nám vyloupnou ve jmenovateli, jsou větší než jedna
– takže z nich opět můžeme ukousnout celou část a pak
pokračovat dál, močálem temným kolem bílých skal.
Tyhle dva procesy trpělivě opakujeme až do okamžiku, kdy dostaneme zlomek, který má jedničku v čitateli. Tam končíme. Musíme ovšem velice přesně kopírovat všechny zlomkové čáry, abychom se do toho nezamotali. Jako příklad si spočítáme řetězový zlomek čísla 38/29. Dole vidíte v prvních dvou rovnicích oba základní kroky: nejprve ukousneme celou část a pak hodíme zbytek (zde 9/29) do sklepa. Než budete pokračovat dál, dobře si je rozmyslete. Protože pak už jenom opakujete to samé. Všimněte si (na konci prvního řádku), že nám v mezivýsledku vyšly 2/9, a protože v čitateli zatím nemáme jedničku, musíme pokračovat dále. Tedy hodit do sklepa, ukousnout celou část a pak už to vyjde (to, že se po konečném počtu kroků k jedničce v čitateli vždy propracujeme, je garantováno tzv. Euklidovým algoritmem, který s řetězovými zlomky velice úzce souvisí).
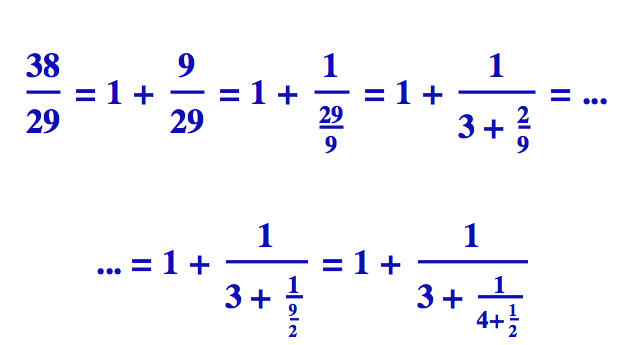
Takže 38/29 se dá ve formě řetězového zlomku zapsat takto [1;3,4,2].
To, co jsme se právě naučili se zlomky, se dá provést s libovolnými čísly, klidně i s iracionálními (ale musíte je mít vyčíslena na dostatečný počet desetinných míst). Pro iracionální čísla se proces ovšem nikdy nezastaví (takže dostanete nekonečný rozvoj). To není nic překvapivého, protože i jejich desetinný rozvoj je nekonečný a řetězový zlomek není nic jiného než zápis daného čísla v jiném formátu. Koneckonců, kdyby mělo iracionální číslo konečný řetězový zlomek, tak by se dalo převést na zlomek normální, a to je logický nesmysl. Jako příklad si zkusíme mé oblíbené iracionální číslo – přirozený logaritmus 9: ln(9) = 2.19722... Opět si všimněte, že v prvních dvou krocích níže ukousneme celou část a zbytek hodíme do sklepa. Musíme si ovšem trochu pohrát s kalkulačkou, abychom zjistili, že 1/0.19722... = 5.07036 (jinak je to ale pořád ta samá sklepní rovnice jako nahoře).
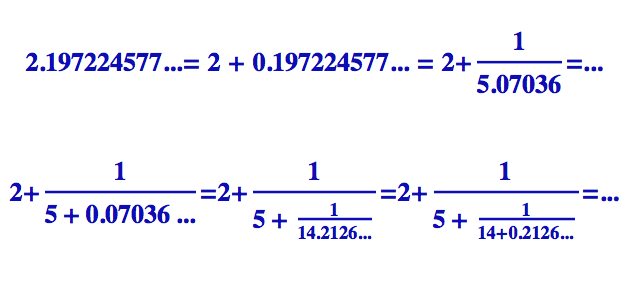
Tady vidíme, že (nekonečný) řetězový zlomek pro ln(9) začíná takto
[2;5,14,...]. Kdybychom měli k dispozici ještě přesnější desetinný
výraz, mohli bychom pokračovat a dostat v principu kompletní řetězový
rozvoj:
ln(9) = [2;5,14,4,1,2,2,8,1,15,1,2,1,8,2,7,...]. Všimněte si, že zatímco v desetinném rozvoji najdete – z povahy věci – pouze čísla mezi 0 a 9, v řetězovém rozvoji se mohou objevit libovolně velká čísla, protože nejste
omezeni žádným pevným základem (např. ve výše uvedeném rozvoji vidíte
čísla 14 a 15).
Teď si jistě říkáte, proč by se takovou habaďůrou vůbec někdo zabýval – desetinný rozvoj tohoto čísla (tedy 2.197224577...) je přece daleko jednodušší než jeho řetězový rozvoj [2;5,14,4,1,2,2,8,1,15,1,2,1,8,2,7,...]. Ve zbytku této sekce se vás pokusím přesvědčit, že rozvoj do řetězového zlomku má určité přednosti a občas nám o číslech prozradí věci, které bychom z desetinného rozvoje nikdy nevyčetli.
Vezměme si nejprve racionální čísla, tedy zlomky jako takové. Jejich desetinný rozvoj je buď konečný (např. 4/5 = 0.8), a nebo nekonečný s periodou (např. 8/3 = 2.66666...). Pro řetězové zlomky žádné takové „buď, a nebo“ není. Každý zlomek má konečný řetězový rozvoj a tím to hasne.
Ještě zajímavější je situace u nejjednodušších iracionálních čísel – druhých odmocnin (z typografických důvodů je budu značit „kalkulačkovým“ výrazem sqrt). Podívejme se teď, jak si v desetinném zápisu stojí odmocniny z celých čísel (a vynechám čtverce, protože ty mají odmocniny celočíselné).
sqrt(2) --- 1.41421356237309504880168872420969807856967187537695...
sqrt(3) --- 1.73205080756887729352744634150587236694280525381038...
sqrt(5) --- 2.23606797749978969640917366873127623544061835961153...
sqrt(6) --- 2.44948974278317809819728407470589139196594748065667...
sqrt(7) --- 2.64575131106459059050161575363926042571025918308245...
sqrt(8) --- 2.82842712474619009760337744841939615713934375075390...
sqrt(10) --- 3.16227766016837933199889354443271853371955513932522...
sqrt(11) --- 3.31662479035539984911493273667068668392708854558935...
sqrt(12) --- 3.46410161513775458705489268301174473388561050762076...
sqrt(13) --- 3.60555127546398929311922126747049594625129657384525...
sqrt(14) --- 3.74165738677394138558374873231654930175601980777873...
sqrt(15) --- 3.87298334620741688517926539978239961083292170529159...
Vidíme, že všechno jsou to nekonečné desetinné rozvoje, jak se na iracionální čísla sluší a patří. V posloupnostech desetinných čísel však nenajdete žádnou pravidelnost ani periodu. Čísla vypadají, jako by je z osudí zcela náhodně vytahal sousedův papoušek. Zkrátka chaos.
A teď se podívejme na rozvoje stejné skupiny čísel do řetězových zlomků (máte-li dostatečně přesnou kalkulačku, můžete si prvních pár členů spočítat sami jako cvičení).
sqrt(2) ---
[1;2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,2,...]
sqrt(3) ---
[1;1,2,1,2,1,2,1,2,1,2,1,2,1,2,1,2,1,2,1,2,1,2,1,2,1,2,1,2,1,...]
sqrt(5) ---
[2;4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,4,...]
sqrt(6) ---
[2;2,4,2,4,2,4,2,4,2,4,2,4,2,4,2,4,2,4,2,4,2,4,2,4,2,4,2,4,2,...]
sqrt(7) ---
[2;1,1,1,4,1,1,1,4,1,1,1,4,1,1,1,4,1,1,1,4,1,1,1,4,1,1,1,4,1,...]
sqrt(8) ---
[2;1,4,1,4,1,4,1,4,1,4,1,4,1,4,1,4,1,4,1,4,1,4,1,4,1,4,1,4,1,...]
sqrt(10) ---
[3;6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,6,...]
sqrt(11) ---
[3;3,6,3,6,3,6,3,6,3,6,3,6,3,6,3,6,3,6,3,6,3,6,3,6,3,6,3,6,3,...]
sqrt(12) ---
[3;2,6,2,6,2,6,2,6,2,6,2,6,2,6,2,6,2,6,2,6,2,6,2,6,2,6,2,6,2,...]
sqrt(13) ---
[3;1,1,1,1,6,1,1,1,1,6,1,1,1,1,6,1,1,1,1,6,1,1,1,1,6,1,1,1,1,...]
sqrt(14) ---
[3;1,2,1,6,1,2,1,6,1,2,1,6,1,2,1,6,1,2,1,6,1,2,1,6,1,2,1,6,1,...]
sqrt(15) ---
[3;1,6,1,6,1,6,1,6,1,6,1,6,1,6,1,6,1,6,1,6,1,6,1,6,1,6,1,6,1,...]
Tady už je na první pohled vidět zcela pravidelné schéma. Každá odmocnina má určitou periodu a ta se potom neustále opakuje. A to platí pro všechny kvadratické iracionality (tedy kořeny kvadratických rovnic s celočíselnými koeficienty). To mimochodem není žádná novinka. Tyto rozvoje byly známy už Eulerovi a Lagrangeovi v 18. století.
Na závěr se podíváme na transcendentní čísla e (základ přirozených logaritmů) a π (podíl obvodu a průměru kružnice). Tato čísla patří v matematice k nejmystičtějším, protože nesplňují žádnou algebraickou rovnici. Nejprve desetinný rozvoj:
π = 3.14159265358979323846264338327950288419716939937511...
e = 2.71828182845904523536028747135266249775724709369996...
Vidíte, že z desetinného pohledu jsou obě čísla v podstatě stejně záhadná a jejich rozvoj se v obou případech jeví zcela náhodným a zbaveným jakéhokoliv vnitřního řádu. Řetězový rozvoj je ovšem jiné kafe. Tady se ukáže, že Ludolfovo číslo je přece jenom o něco tajemnější. Zatímco číslo e vykazuje velice pravidelnou strukturu, π je stále jen náhodná snůška jmenovatelů.
e =
[2;1,2,1,1,4,1,1,6,1,1,8,1,1,10,1,1,12,1,1,14,1,1,16,1,1,18,1,1,20,...]
π =
[3;7,15,1,292,1,1,1,2,1,3,1,14,2,1,1,2,2,2,2,1,84,2,1,1,15,3,13,1,4,...]
Takže, pánové, baterku do ruky, Ludolfovo číslo (v řetězovém rozvoji!) na papír a za vlahé letní noci vyslat do vesmíru následující posloupnost bliknutí (x=krát): 3x, 7x, 15x, 1x, 292x, 1x, 1x, 1x, 2x, ... (Yoothix čeká!)
Doporučená četba:
A. J. Chinčin: Řetězové zlomky
Hans Rademacher: Higher Mathematics from an Elementary Point of
View
Joe Roberts:
Elementary Number Theory
Continued
Fraction Calculator (interaktivní stránka pro experimentování)
Stern-Brocotův strom - druhé podání
(tady bych doporučil vydatnou pauzičku)
Dosud to bylo jen takové opáčko ze středoškolské matematiky, teď se ale podíváme, jak nám řetězové zlomky pomohou při pochopení struktury Stern-Brocotova stromu (viz minulé Matykání). Na zahřátí si v něm najdeme zlomek 4/11 a zvýrazníme si cestu k němu z bodu jedna (tedy 1/1). Protože z každého zlomku vybíhají směrem dolů dvě větve, současně si označíme, zda vybíráme větev Levou nebo Pravou.
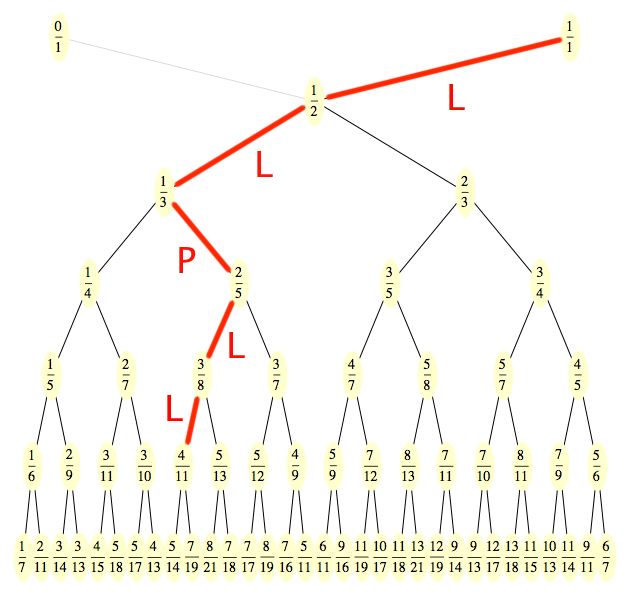
Takže do bodu 4/11 se dostaneme podle itineráře L-L-P-L-L (je to stejné, jako když jedete po městě a manželka vám radí: doleva, doleva, doprava, doleva, doleva). Všimněte si, že v itineráři se pravidelně střídají skupiny písmenek L a P. V našem případě máme dvě L, pak jedno P a pak zase dvě L. Aby byl itinerář co nejúspornější, zapíšeme si pouze, kolik písmenek v každé skupince je (písmenko si zapisovat nemusíme, protože ta se pravidelně střídají a první krok je vždy L – jinak bychom se ocitli mimo náš diagram). Takže itinerář pro cestu do 4/11 je teď prostě {2,1,2}.
Teď jednu technickou poznámku. Řetězové zlomky v sobě skrývají jednu malou nejednoznačnost. Zlomek 1/4 je to samé jako 1/(3 + 1/1), přičemž oba zápisy jsou zcela regulární řetězový zlomek. A ta jednička se dá z posledního členu vždycky „utrhnout“ – například [1;2,3] je to samé jako [1;2,2,1]. Tohle, mimochodem, není žádná tragédie, u desetinných čísel máme také dvě možnosti zápisu: 0.17 = 0.169999999... Takže si prostě pamatujte, že poslední člen řetězového zlomku, říkejme mu [...,x], se dá vždycky zapsat jako [...x – 1,1]. A je na vás, kterou formu si vyberete. Někteří autoři jedničku na konci preferují (dává řetězovému zlomku určitou uniformitu), jiní preferují zápis, který jsem si vybral já.
A teď zpátky k našemu příkladu se 4/11. Spočítáme si jejich řetězový zlomek a dostaneme [0;2,1,3], což můžeme s ohledem na minulý odstavec přepsat jako [0;2,1,2,1]. Poslední jednička je jen taková kotva, kterou má každý řetězový zlomek v jedničkovém tvaru, takže ji bez váhání vyhodíme (to se s kotvami běžně dělá) a zůstane nám posloupnost {2,1,2}. Ta je shodou okolností přesně shodná s itinerářem, který nás k tomu zlomku dovedl. A to prosím není žádná náhodička. Takhle to přesně funguje. Řetězové zlomky jsou jakousi GPSkou pro pohyb po Stern-Brocotově stromu.
Teď také konečně vidíme, že Stern-Brocotův strom opravdu obsahuje všechna racionální čísla. Každé má svůj řetězový zlomek a ten vás k tomu číslu spolehlivě navede.
Na procvičení si najděte itinerář pro červenou cestu z bodu 1/1 do bodu 4/13 – vyjde vám {3,3} – tedy tři kroky doleva a pak tři doprava. A když si spočítáte řetězový zlomek pro 4/13, dostanete [0;3,4]. Ten přepíšeme v jedničkové konvenci jako [0;3,3,1], poslední jedničku zahodíme a máme opět tu samou posloupnost: {3,3}. Jo, a pokud to někomu vrtá hlavou, tak úvodní nulu můžeme taky vyhodit, protože tu mají všechny zlomky mezi 0 a 1. Jinými slovy, ta nám nepřináší žádnou informaci.
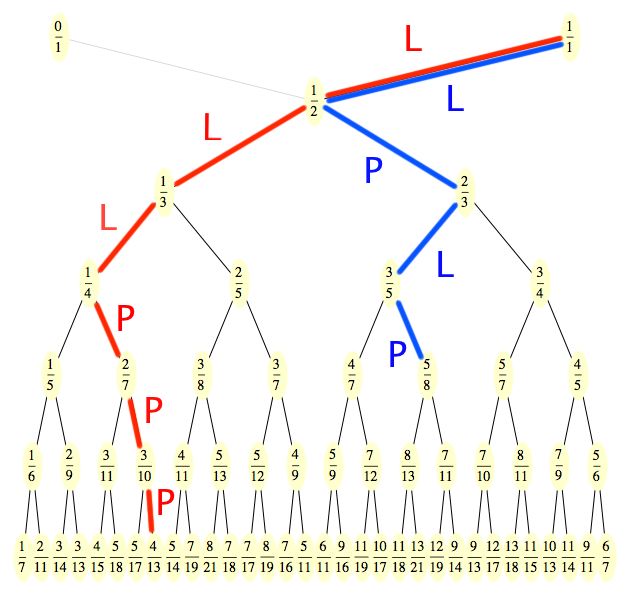
Teď si to zkusíme pro modrou cestu. Z řetězového zlomku si sestavíme itinerář a ten nás k číslu dovede. Zlomek 5/8 má řetězový rozvoj [0;1,1,1,2]. Závěrečnou dvojku napíšeme jako dvě jedničky (jedničkový formát), tu poslední vyhodíme (je to jenom kotvička) a dostaneme posloupnost {1,1,1,1}. A to je přesně itinerář pro výlet ke zlomku 5/8: jeden krok doleva, jeden doprava, jeden doleva a jeden doprava.
Tohle samozřejmě není žádný zázrak. Souvislost cestovních itinerářů a řetězových zlomků vyplývá z role, kterou Stern-Brocotův strom hraje v teorii diofantických rovnic, tedy rovnic, ve kterých nás zajímají pouze celočíselná řešení. Tahle partie matematiky je ale poměrně zapařená, tak vám ji odpustím a dáme si jen malý příklad: najděme si zlomek 2/5 a sledujme větev, která z něj vychází doleva: 2/5, 3/8, 4/11, 5/14, 6/17... Na každý takový zlomek se můžeme dívat jako na dvojici čísel (2, 5), (3, 8) a tak dále. Všimněte si, že všechny tyto dvojice čísel splňují diofantickou rovnici 3X – Y = 1 (dají se do ní dosadit za X a Y). A taková lineární rovnice se dá najít pro každou větev Stern-Brocotova stromu. A taky naopak. Kdykoliv máte diofantickou rovnici aX – bY = 1, tak existuje větev Stern-Brocotova stromu, která v sobě obsahuje všechna její (celočíselná) řešení.
Jinými slovy, Stern-Brocotův strom je v podstatě jakýmsi lexikonem řešení lineárních diofantických rovnic. A řetězové zlomky se v matematice používají jako mechanická pomůcka pro nalezení té správné větve. To už bychom ale zabředli do zbytečně technických detailů. Koho to zajímá podrobněji, doporučuji prostudovat výše citovanou knížku Joea Robertse a nebo jakoukoliv solidní učebnici teorie čísel.
Na závěr této sekce ještě malou filozofickou poznámku.
Zlomky, ač na to nevypadají, žijí dvojím životem. Tak trochu jako Oldřich Nový ve filmu Kristián. Přes den pracují v aritmetickém úřadě, kde trpělivě provádějí výpočetní operace, které na ně klademe, a v noci se noří do ezoterického světa diofantických rovnic, kde hrají úplně jinou roli. Roli tajuplných a světácky se usmívajících elegánů.
Zajímavé je, že aritmetický a diofantický svět (stejně jako ve filmu Kristián) o sobě prakticky nevědí. Nejlépe je to vidět, když si vezmete dva zlomky a napíšete si jejich řetězový rozvoj. Pak s nimi udělejte nějaký aritmetický fígl, třeba je sečtěte nebo vynásobte, a výsledek opět rozviňte v řetězový zlomek. A teď si zkuste najít algoritmus, který ten řetězový zlomek výsledku vydyndá z původních řetězových zlomků. Uvidíte, že je to poměrně těžký oříšek. Řetězové zlomky nejsou zrovna kompatibilní s aritmetickými operacemi a naopak. Tato zvláštní izolovanost diofantického a aritmetického světa leží podle mého názoru u kořene mnoha problémů z teorie čísel.
Sekce jauvajs: Modulární grupa
(pouze pro mimořádně otrlé jedince)
Stern-Brocotův strom nám také umožňuje následující zajímavou konstrukci. Vezmeme si nějaký zlomek, řekněme 5/13, a ze Stern-Brocotova stromu si odečteme jeho tatínka a maminku: zde 2/5 a 3/8 (viz minulé Matykání). Tyto zlomky pak jako dvojice čísel umístíme do sloupců čtvercové matice 2x2.
| 2 3 |
| 5 8 |
Všimněte si, že determinant této matice (tedy rozdíl součinu hlavní a vedlejší diagonály) je jedna: 2x8 – 3x5 = 1. Množině celočíselných matic s jednotkovým determinantem se říká „modulární grupa“, protože když dvě takové matice vynásobíte, dostanete prvek té samé množiny (a obdobně pro inverzní matici).
Z každého zlomku si tedy tímto způsobem vytvoříme jeden prvek modulární grupy a naopak. Každá taková matice je tvořená sloupci, které si můžete představit jako dva zlomky, jejichž Fordovy kružnice jsou tečné (tj. jsou tatínkem a maminkou pro nějaký jiný zlomek). Stern-Brocotův strom tak vlastně představuje mapu modulární grupy a umožňuje nám vytvořit si obrázek, jak taková grupa vlastně vypadá, což je pro nekonečnou grupu velice vítaná možnost (na rozdíl od grup konečných si je totiž nelze znázornit tabulkou).
Modulární grupa hraje v teorii čísel významnou roli, například v tom, že má v sobě zakódováno, jak faktorizovat dvě po sobě jdoucí čísla. Vezměme si například čísla 35 a 36. To první můžeme roznásobit jako 5x7 a to druhé jako 4x9. Pokud tato čísla umístíme na vedlejší a hlavní diagonálu, získáme jeden prvek modulární grupy, v našem případě tuto matici:
| 4 7 |
| 5 9 |
A takhle si můžeme nabrnkat všechny prvky modulární grupy. Každá faktorizace dvou po sobě jdoucích celých čísel nám vygeneruje nový prvek grupy. Tam, kde je jedno z čísel prvočíslo, bude faktorizací samozřejmě méně. To, že se tak nepravidelná struktura, jako je dělitelnost po sobě jdoucích čísel, dá zakódovat do tak pravidelného objektu, jako je algebraická grupa, mi přijde jako jeden z nejfantastičtějších fenoménů, se kterými jsem se kdy v matematice setkal.
A na úplný závěr ještě jeden zajímavý obrázek, který nám ukáže, jak komplikovanou vnitřní strukturu modulární grupa má. Na osu x budu vynášet racionální čísla ze Stern-Brocotova stromu (tedy zlomky mezi 0 a 1) a na osu y pak vynesu úhel mezi vlastními vektory matice, která ze zlomku vznikne výše popsaným způsobem.
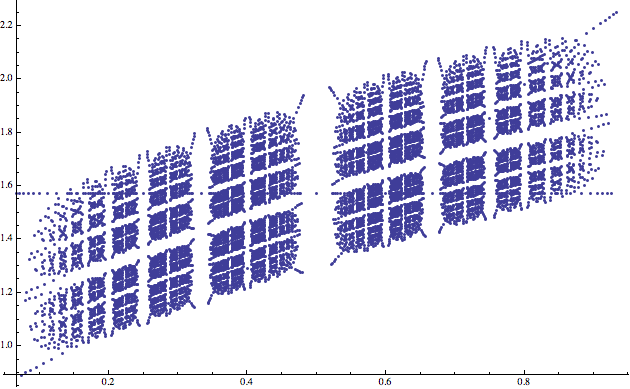
Tento obrázek vznikl z prvních 4000 zlomků Stern-Brocotova stromu (počítáno seshora). Stern-Brocotův strom ale zlomky z intervalu (0, 1) nevybírá rovnoměrně. Můžete si například všimnout, že kolem 1/2 je poměrně pusto (proč tomu tak je, uvidíme v příštím Matykání). Pokud bychom si zlomky vybrali rovnoměrně (například tak, že bychom uvažovali všechny zlomky mezi 0 a 1, jejichž jmenovatel je menší než 200), obrázek by vypadal takto.
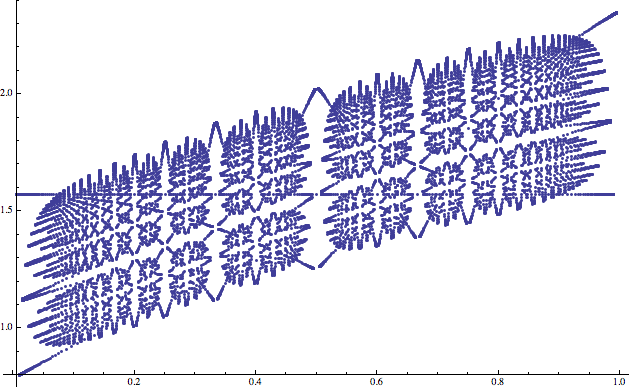
Mimochodem, na obou obrázcích je vidět vodorovná linie zhruba v hodnotě y = 1,57. Ta odpovídá racionálním číslům, pro které je matice složená z tatínka a maminky symetrická (v takovém případě totiž vlastní vektory svírají pravý úhel, což je zhruba 1,57 radiánů).
Článek je redakčně upravenou verzí blogového příspěvku na serveru
iDNES.cz. Publikováno s laskavým svolením autora.
Další díly a původní texty jsou dostupné na blogu Jana Řeháčka.