Pokud se rádi rácháte v číslech a přemýšlíte, co s kariérou, nabízí se bouřlivě se rozvíjející odvětví strojového učení (machine learning). Nu, dali jsme světu „učitele národů“, tak proč bychom nemohli přihodit i učitele nástrojů.
Jistě jste si všimli, že když začnete něco ťukat do vyhledávače, tak vám stroj (zde prohlížeč) nabídne několik populárních možností, včetně těch, které jste vy sami už kdysi hledali. Nebo si někde na Internetu koupíte hodinky s vodotryskem a hned na vás začnou ze všech stran obrazovky vykukovat průtokové kašny s vestavěným ciferníkem.
Ať chceme či nechceme, stroje nás šmírují a snaží se z našeho chování zjistit, co vlastně chceme – aby to mohly obratem páky pošeptat někomu, kdo to produkuje. A jak budou stroje chytřejší a chytřejší, tato „vnímavost“ se bude pravděpodobně prohlubovat, až se jednoho dne dobereme k umělé inteligenci, kdy budeme se strojem schopni přímo komunikovat.
V tradičním programovacím schématu člověk počítači přesně sdělí, jak se má v každé dané situaci zachovat: „POKUD déšť, PAK vytáhni deštník, JINAK přibal slunečník.“ Moderní doba nás ovšem zaplavuje daty s takovou rychlostí, že už není možné stroji přesně nahustit do obvodů, jak se má pro každou možnou konfiguraci dat zachovat. Těch dat je příliš mnoho. A jediný, kdo má šanci je přečíst a vstřebat je právě stroj.
A tak je nutno začít stroje trpělivě učit, aby se v té záplavě dat uměli vyznat sami. Jenže aby stroj z toho stohu informací dokázal vycucat nějaké užitečné vztahy a abstraktní zákonitosti, musí dostat určitou algoritmickou svobodu: musí mít možnost se volně pohybovat v nějakém parametrickém prostoru a pružně reagovat na změny v toku a charakteru dat.
Nižší formě tohoto úsilí se říká „strojové učení“ (machine learning), zatímco pro vyšší se vžilo označení „umělá inteligence“ (artificial intelligence). Hranice mezi klasickým programováním a těmito novými paradigmaty je pochopitelně do jisté míry mlhavá a ještě ne zcela usazená. Já chápu strojové učení jako schopnost orientovat se v určitém speciálním kontextu, zatímco umělou inteligenci vidím spíše ve zvládnutí přechodu do kontextů zcela nových.
Strojové učení se v tomto vidění světa umí vypořádat s jednoduchými úkoly v rámci stabilního prostředí, např. dokáže rozpoznat určité typy objektů či vysledovat trendy ve strukturovaných datech. Umělá inteligence dokáže aplikovat (resp. překládat) poznatky z jiných vědomostních okruhů, a zvládne tudíž i komplexní činnosti vyžadující souhru několika relativně autonomních podsystémů (např. řízení auta).
Zatímco dnešní „vyučené“ algoritmy vám po návratu z dovolené v Řecku budou ještě dalšího půl roku nabízet tutéž destinaci, „umělý inteligent“ budoucnosti pochopí, že pokud si něco koupíte, tak to nějaký čas nebudete potřebovat, a zaměří se na jiné oblasti. Jeho všudypřítomná čidla si například všimnou, že se vám třepí podrážky a komunikační modul vám nenápadně začne nabízet nové boty.
Do jaké míry se nám podaří tu umělou inteligenci dotáhnout až do stadia sebereflexe (kdy se počítač plácne robotickým chapadlem do čela a uvědomí si, že je počítač, a ne třeba medvídek mýval), je otázka spíše filosofická, a abych nezabředl do dalekosáhlých úvah o tom, co je to vědomí, raději se jí vyhnu. Stejně jako možným eticko-morálním otázkám soužití lidí a chytrých strojů. To bychom tu byli do léta.
V tomto Matykání se soustředím na pár základních principů strojového učení a pro ilustraci vám ukážu pár příkladů, jak na to ti kovoví koumáci vlastně jdou.
Trénink, test a predikce
Než začneme hloubat, jak se učí stroje, podívejme se sami na sebe. Jak se třeba naučíme rozlišovat mezi kočičkami a pejsky? Nu, jednoduše. Ťapkáme si s maminkou po světě a maminka nám trpělivě ukazuje příklady: „Tohle je kočička, a ne pejsek.“ A u boudy naopak: „To vevnitř je pejsek – žádná kočička, ty trumpeto.“ A capart si začne všímat, že kočičky a pejskové mají různé atributy (kterým se ve strojovém učení říká též fíčury – z angl. features)). Například pejsek je obvykle větší a umí plavat. Kočička bývá menší a plavat neumí. Umí ale lézt na stromy, což zase neumí pejsek. A capart si postupem času různou kombinací těchto atributů vytvoří ve své hlavičce poměrně spolehlivý algoritmus na rozlišování pejsků a kočiček.
Tu posloupnost příkladů, kterými nás maminka zásobuje, si můžeme schematicky zapsat pomocí matice, které se v tomto kontextu často říká datová tabulka (angl. dataframe). Každý příklad je samozřejmě nutno doprovodit tzv. „nálepkou“, která nám říká, zda je uvedený příklad kočička anebo pejsek. Atributy se obvykle značí x a nálepka y (pro obě kategorie existuje v literatuře obrovské množství synonym, např. nezávislé a závislé proměnné, input a output, prediktor a regresand atd).
Datová tabulka T pro n příkladů s m atributy
x1[1] x2[1] x3[1] ... xm[1] ---> y[1]
x1[2] x2[2] x3[2] ... xm[2] ---> y[2]
x1[3] x3[3] x3[3] ... xm[3] ---> y[3]
....
x1[n] x2[n] x3[n] ... xm[n] ---> y[n]
(hranatá závorka indexuje jednotlivé příklady)
Takhle tedy vidí pejsky a kočičky počítač. Hezky mu tu matici T naservírujeme a necháme ho, aby si z příkladů vytvořil nějaký model reality, který mu umožní správně oba živočichy klasifikovat. Jak to udělá? Na to existují desítky algoritmů a na pár z nich se za chvíli podíváme.
Matice T tedy při strojovém učení hraje roli maminky, která počítači prozradí, zda daný řádek (tedy kolekce atributů) reprezentuje kočičku či pejska. Aby se ale dalo ověřit, že počítač se naučil zvířátka rozlišovat správně, je nutno výsledný algoritmus otestovat, a teprve potom ho můžeme pustit k samostatnému určování. Proto má vývoj určovacího softwaru obvykle tři fáze: trénink, test a predikce.
V praxi si kromě matice T připravíme ještě (ze stejného zdroje) matici T°, která je obvykle menší a počítač ji během trénovací fáze nevidí. Tréninková matice T se pak naláduje do stroje a ten se z ní pokusí vytvořit klasifikační algoritmus, který každé množině atributů x přiřadí určitou nálepku y' (např. 0 = kočička, 1 = pejsek). Tím končí trénink trénink. Když je algoritmus nalezen, do počítače se naláduje testovací množina T° a počítačem předpovězené nálepky y' se porovnají s těmi skutečnými y. Pokud je testování úspěšné a algoritmu se v té testovací množině podařilo správně rozlišit uspokojivé procento příkladů (typicky 80 – 100 %), daný model se uloží a slouží potom k vlastní predikci. Atributy x nového příkladu živočicha se hodí do stroje a ten vyplivne nálepku y', která nám prozradí, zda je to kočička anebo pejsek.
Shrnuto a podtrženo: namísto, abychom trápili programátora s vymýšlením přesného klíče k určování zvířátek (a riskovali, že se nám ztratí v bludišti atributů), tak stroji prostě ukážeme pár příkladů a necháme ho, aby si – v rámci předem definovaných mantinelů – to bludiště vymyslel sám.
Z pohledu matematiky je takový klasifikační algoritmus de facto hledání funkce F, která spojuje kolekce atributů x s nálepkami y. Samozřejmě je závislost zamaskovaná spoustou nahodilých vlivů, které do problému vnesl život (někteří pejskové nedorostou do běžné velikosti, některé kočičky se naučí plavat atd.). Funkce, kterou pozorujeme, má tedy realisticky vzato tvar: y = F(x) + ε, kde ε reprezentuje náhodné hodnoty. Úkolem strojového učení je tyto náhodné vlivy odfiltrovat a objevit tu skutečnou funkci F. A to je docela fuška i bez náhodných vlivů: představte si, že vám na tabuli nakreslím osový kříž, do něho načmárám šest bodů a zeptám se vás, co je to za funkci (respektive která funkce těmito body prochází).
Navíc musíme mít na paměti, že ne všechny atributy jsou reálná čísla: některé mohou být diskrétní atributy (barva srsti: černá, šedá či bílá), jiné mohou být binární (umí to plavat: ANO či NE). Takové se musí v mnoha algoritmech nejprve převést na čísla, aby se s nimi mohlo rozumně pracovat. Obvykle stačí atributy očíslovat (černá 0, šedá 1 a bílá 2), ale někdy je výpočetně výhodnější je označit binárními vektory, které mají všude nulu, jen pro příslušnou komponentu 1: černá (1,0,0), šedá (0,1,0) a bílá (0,0,1). V angličtině se tomuto triku říká one-hot encoding.
Klasifikační proces v mnoha ohledech připomíná regresi, kde se z nezávisle naměřených hodnot x snažíme odhadnout hodnoty závislé proměnné y. Například z různých atributů x nějakého obytného domku se můžeme pokusit předpovědět jeho prodejní cenu y. Takovými atributy může být např. počet místností (celé číslo), celková obytná plocha (reálné číslo), zda má domek garáž (binární ANO či NE), jak daleko je do centra (reálné číslo) atd.
To není náhoda, na regresi se v jistém smyslu můžeme dívat jako na spojitou klasifikaci (nálepka y nabývá libovolné reálné hodnoty). A stejně jako nálepka „kočička-pejsek“ klasifikuje domácího mazlíčka, nálepka „cena domu“ také v jistém smyslu ten dům klasifikuje (na škále mansarda-pastouška). Ale činí tak spojitým způsobem.
Anebo obráceně: na klasifikaci se můžeme dívat jako na diskrétní regresi (kde závislá proměnná y nabývá pouze diskrétních hodnot).
Zkrátka, na regresi a klasifikaci se můžeme dívat jako na dvě strany téže mince. A to je další příklad kontinentálního zlomu spojitost-diskrétnost, o kterém jsem kdysi referoval.
Typologie strojového učení
Takže si to zopakujme. V předešlé sekci jsme se zabývali problémem, jak z dané množiny atributů odhadnout nějakou diskrétní (klasifikace) či spojitou (regrese) veličinu. Za tím účelem jsme si sestrojili matici příkladů T, sestávající se v podstatě z dvojic (x, y), kde x je vektor atributů a y je spojitá či diskrétní nálepka (on to v některých případech může být i vektor, ale s tím si nebudeme lámat hlavu). A počítač má za úkol z těchto příkladů objevit přiřazovací funkci F: x --> y.
Každý algoritmus obsahuje několik tzv. hyperparametrů, které zadává člověk, a pak několik parametrů (např. koeficienty polynomu při regresi), které si počítač propočítává sám během trénovací fáze. V testovací fázi pak algoritmu nabídneme obdobnou matici T', zaznamenáme si, jaké nálepky y' z daných atributů x předpovídá, kde y' = F(x), a tyto pak porovnáme se skutečnými nálepkami y z testovací množiny.
V diskrétním případě je nejpřirozenějším způsobem porovnání procento úspěšných klasifikací – i když existují i jemnější způsoby, jak účinnost nově vzniklého klasifikátoru ocenit – např. ROC křivky nebo matice zmatenosti (ne nedělám si srandu).
Ve spojitém případě je nejjednodušší podívat se na akumulovaný rozdíl mezi předpovězenými a skutečnými hodnotami, tj. Σ(y'-y)2.
Pokud je chyba příliš velká, můžeme se pokusit přeštelovat hyperparametry metody a trénovací proces zopakovat (tomu se říká ladění hyperparametrů).
Důležité je, že jak v diskrétním, tak ve spojitém případě má stroj k dispozici nálepky, které mu umožňují se lépe orientovat v terénu. A protože ty nálepky zadává lidský „učitel“ (ať je to programátor či maminka), mluvíme v tomto případě o učení s učitelem (supervised learning).
To je pochopitelně nákladné, protože někdo (člověk, kterého je nutno zaplatit) musí ty nálepky nějakým způsobem připravit (z měření, z historických dat atd.). Proto se v mnoha případech používá tzv. učení bez učitele (unsupervised learning). Do stroje se nasypou pouze vektory atributů x a algoritmus se pak pokusí v tomto mnoho-dimenzionálním „oblaku bodů“ najít nějakou strukturu.
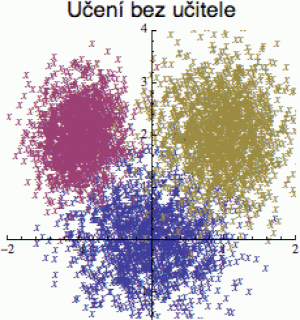
Pokud například do počítače nasypeme zvířecí atributy, které po různých transformacích a redukcích vypadají jako obrázek vpravo, dá se předpokládat, že použitá data obsahovala tři podobná zvířátka (např. pejsek, kočička a prasátko). Počítač samozřejmě netuší, kdo je kdo (nemá nálepky), takže jim musí říkat zvířátko č. 1, č. 2 a č. 3 – ale to nám v mnoha případech stačí.
Další významnou aplikací učení bez učitele je strojové zpracování textu (NLP). Představte si, že potřebujete zjistit, která slova jsou významově blízká (abyste se při vyhledávání mohli opřít i o synonyma). Stačí, aby se počítač naučil reprezentovat text pomocí vektorů, a může se pustit do zkoumání struktury jazyka či celých textových korpusů. Takové algoritmy existují jak na úrovni jednotlivých slov (např. word2vec), tak na úrovni dokumentů (LSA). A žádného učitele (tedy nálepky) nepotřebují. Všechny zajímavé sémantické vztahy objeví na základě toho, která slova se v textech vyskytují pospolu. Či zrcadlově: které texty obsahují podobná slova.
Prostě nasypete milion textů do stroje a on vám obratem sdělí, které texty či slova se významově podobají. Ten počítač samozřejmě slovům ani textům nerozumí, jen se postupně naučil je vhodně reprezentovat.
Třetí důležitou kategorií strojového učení (vedle učení s učitelem a učení bez učitele) je tzv. zpětnovazební učení (reinforcement learning), které se snaží do domény strojů převést jednu důležitou vlastnost lidské inteligence: často se vyplatí vybrat řešení, které je sice dočasně nevýhodné, ale později vám vynese mnohonásobně vyšší zisk – např. cesta ze sadu do stodoly pro žebřík se zpočátku jeví jako plýtvání energií (stroj by nic takového neudělal), ale nakonec nám umožní sklidit sladší plody. Anebo si to můžete představit jako obětování figury v šachu za účelem získání strategické výhody.
Stroje jsou velmi dobré v lokální optimalizaci, tedy dokáží sledovat řešení, které přináší okamžité výhody. Ale na to, aby se naučili, že občas je třeba vybrat méně optimální cestu, už je třeba speciálních algoritmů. Ty většinou fungují na základě určité rovnováhy mezi používáním již nalezených výhodových vzorců a prozkoumáváním dalších neoptimálních řešení, které by mohly vést k pozdějšímu úspěchu. Navržené systémy většinou fungují tak, že ze začátku se více věnují prozkoumávání prostoru možností za účelem zjištění, v čem spočívají největší odměny, zatímco ke konci vyměřeného času už spíše jen aplikují naučené dovednosti k získávání pamlsků (byť ne nutně těch nejlahodnějších).
Ve zbytku dnešního Matykání se podíváme na tři příklady učení s učitelem, které je v aplikacích o něco rozšířenější než zbylé dvě kategorie. Záměrně se při tom vyhnu neuronovým sítím, na něž se poměrně podrobně podíváme příště.
1. SVM (podpůrné vektory)
Asi nejpřirozenější metodou pro klasifikaci je situace, kdy máme dva typy objektů a jejich atributy lze v příslušném prostoru oddělit nadrovinou – jak je naznačeno vpravo na obrázku (a). Zde má prostor atributů dimenzi 2 (x1, x2) a nálepky jsem barevně odlišil.
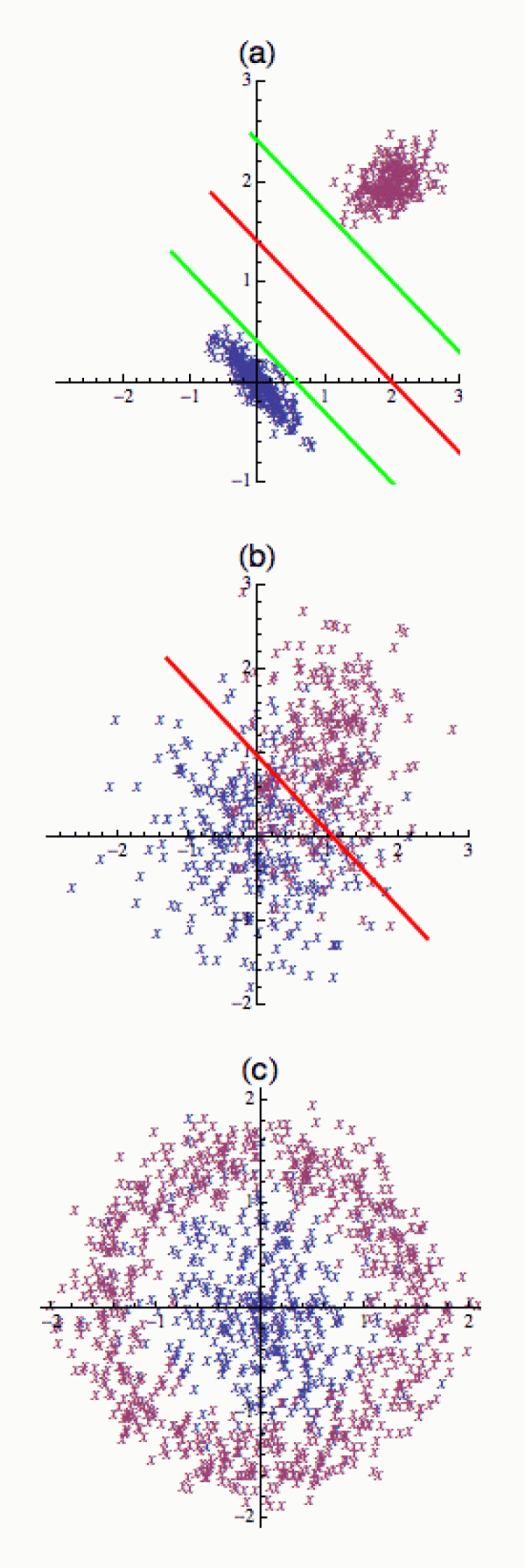
Základem výpočtu je v tomto případě nalezení tzv. rozhodovací hranice (zde červené přímky – ve vyšších dimenzích pak nadroviny), která odděluje příklady jedné skupiny (kočičky) od skupiny druhé (pejskové). Když si v duchu budete s tou červenou přímkou trochu „šmrdlat“, tak zjistíte, že existuje několik poloh, ve kterých dokáže modré a fialové body oddělit. Proto se obvykle hledá poloha, ve které je rozhodovací přímka oddělena od bodů jedné i druhé skupiny co nejširším (zeleným) koridorem, aby se při predikci (kdy uvidíme nové příklady) snížilo riziko chybné klasifikace. Těm bodům, které leží na okraji koridoru, se říká podpůrné vektory – a od nich tato metoda odvozuje své jméno.
Jak se ten koridor najde?
Rovnice přímky, roviny či nadroviny je w.x + b = 0, kde w je vektor normály, x bod prostoru a b skalární posunutí (vzpomeňte si třeba na rovnici nějaké roviny: 2x -3y + z – 1 =0, zde w bude (2,-3,1)). Tyto parametry budou odpovídat rozhodovací hranici. Když s tou konstantou b začneme pohybovat, tak se příslušná nadrovina bude po našem prostoru přemisťovat „rovnoběžně“ (tj. bude mít stále stejnou normálu).
Jednotky zvolíme tak, že zelené okraje koridoru budou odpovídat hodnotám w.x + b = 1 a w.x + b = -1. No a zbytek už je jen poměrně pracná vázaná optimalizace. Hledáme normálový vektor w tak, aby měl koridor maximální možnou šířku (a při tom dbáme na to, aby všechny modré body ležely na jedné straně koridoru a fialové na druhé). Detaily vás nebudu děsit, ale obecně se o optimalizaci zmíním níže v sekci Jauvajs.
Během tréninku se tedy spočítá ta rozhodovací přímka a vlastní predikce je pak vcelku jednoduchá. To, co leží na jedné straně hranice, jsou kočičky. To, co na druhé, pejskové. Takhle fungují třeba některé programy, které určují, zda je nový e-mail ve vašem kastlíku spam anebo ne.
Zajímavá situace nastane, pokud modré a červené body (v daném prostoru atributů) nelze oddělit – jak je naznačeno na obrázku (b). Pak je nutno buď zkusit najít lepší atributy, anebo se smířit s tím, že rozhodovací hranice už nedokáže přesně oddělit jednotlivé příklady, a pak se optimalizací nalezne alespoň přímka, která těch chyb udělá nejméně (opět v červeném). Tomuto přístupu se říká soft-margin (tomu předchozímu – s koridorem – hard margin).
V praxi se občas stane, že atributy příkladů, které algoritmus vidí v tréninkové fázi, se sice jakž takž oddělit dají, ale ne lineárně – jak je naznačeno na obrázku (c). Pak je nutno k oddělení fialových a modrých příkladů použít nějakou zakřivenou plochu, která se pochopitelně hledá obtížněji. V tomto případě naše chmury rozptýlí tzv. kernelový trik (kde kernel je funkce, která v podstatě supluje skalární součiny používané v lineárním případě). Řečeno lidově: ta rozhodovací hranice se musí pomocí kernelové funkce vhodně „ohnout“.
2. Logistická regrese
Na tenkou hranici mezi klasifikací a regresí poukazuje logistická regrese, která je navzdory svému jménu v podstatě binární klasifikací. Z daného vektoru atributů x se tedy pokusí stanovit nálepku náležící do jedné ze dvou tříd (zde se nálepka obvykle značí y = 0 a y = 1).
Podívejme se nejprve na nejjednodušší případ, kdy máme pouze jeden atribut x.
Na následujícím obrázku je na ose y znázorněn výsledek zkoušky (0 = propadl, 1 = uspěl) v závislosti na počtu hodin studia (osa x) pro několik příkladů. Je to vlastně zobrazení trénovací množiny pro tento problém. Ale stejně jako u lineární regrese, do obecné závislosti zasahují různé výše zmíněné náhodné vlivy reálného života – někdy dřeme jako koně, ale před zkouškou nás zlomyslní spolužáci opijí, jindy se zase na učebnice vyflákneme, ale máme štěstí na otázku.
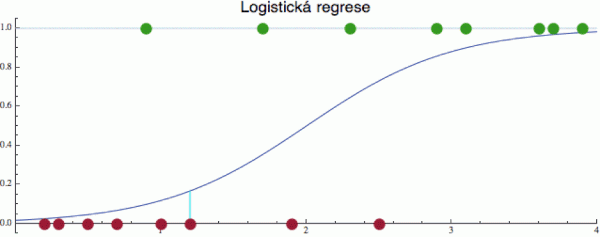
Úkolem je naučit se z výše uvedených dat predikovat výsledek zkoušky na základě studijního úsilí. Ale protože diskrétní nuly a jedničky by se pomocí regrese těžko modelovaly (zkuste si těmi zelenými a červenými puntíky proložit přímku), převede se nejprve celý problém na spojitou pravděpodobnost. Položíme si otázku: Jaká je pravděpodobnost p, že student, který studoval x hodin zkoušku složí?
Pravděpodobnost sice přímkou modelovat také nemůžeme (protože pro dostatečně vysoké hodnoty x by nám vyskočila nad 100 %), ale zkusíme najít nějakou šikovnou modelovací funkci s volitelnými parametry, která se bude blížit k 0 pro malá x a k 1 pro velká x (když hodně studujete, pravděpodobnost úspěchu by se měla blížit 100 %). Tedy zhruba řečeno funkci, která vypadá trochu jako arctg (na obrázku je v tmavě modrém). Takových esíčkovitých funkcí je celá řada a pro potřeby logistické regrese se používá – to byste neuhodli – logistická funkce, která má v základním tvaru vzoreček
L(x) = 1/(1 + exp(-x))
V našem případě bude mít funkční hodnota L(x) význam pravděpodobnosti a do argumentu strčíme lineární funkci atributu x se zatím neznámými parametry a0 a a1.
p = 1/(1 + exp(-a0-a1x))
Když si z této formulky vyjádříte exponenciálu (a zlogaritmujete), dostanete:
ln(p/(1-p)) = a0 + a1x
(a to už lineární regresi hodně připomíná – jen se nám na levé
straně místo závisle proměnné y rozvalila taková... no, jak bych to
řekl... zlý nehezký ošklivá věc)
Zbývá pouze určit hodnotu koeficientů a0 a a1. K tomu nám opět poslouží trénovací množina (jako ta na obrázku nahoře). Pro každou hodnotu koeficientů jsme schopni vyčíslit akumulovanou chybu Σ(L(x)-y). Jednu takovou chybu pro x = 1.2 jsem na obrázku vyznačil bledě modře. Zbytek problému je proto opět optimalizační úloha. V parametrické rovině (a0,a1) chceme najít hodnoty, pro které bude souhrnná chyba co nejmenší.
Stejně jako při tradiční regresi y = a0 + a1x se nemusíme omezit na případy, kdy máme pouze jeden atribut. Výsledek zkoušky může záviset nejen na počtu odstudovaných hodin, ale také třeba na počtu hodin spánku v noci před zkouškou či na momentální hladině alkoholu v krvi. Pokud tedy máme více atributů, sestavíme si prostě lineární kombinaci více proměnných, která bude modelovat tu zlou, nehezkou, ošklivou věc (anglicky se jí říká log-odds ratio):
ln(p/(1-p)) = a0 + a1x1 + a2x2 + ...
A ty kýžené koeficienty se hledají optimalizací v parametrickém prostoru, který má holt trochu víc dimenzí.
Jakmile jsme z trénovací množiny ty koeficienty vycucali (a testovací množina potvrdila, že fungují), můžeme přistoupit k vlastní klasifikaci. Pro každý nový příklad, charakterizovaný atributy x (ať už je jen jeden nebo je jich milion), si spočítáme hodnotu funkce L(x), která nám prozradí pravděpodobnost úspěchu. Pokud bude p > 0.5 znamená to, že nálepka y = 1, pro p < 0.5 bude y = 0.
3. Rozhodovací stromy
Velmi přirozenou metodou strojového učení jsou tzv. rozhodovací stromy, které jsou variací na klasické schéma určování rostlin. Utrhnete si kytičku, na kolena položíte rozevřený klíč a jedete: má to vroubkované listy (ANO-NE), pokud ANO, má to více než 5 okvětních lístků (ANO-NE), pokud NE má rostlina dlouhý řapík (ANO-NE). A tak pokračujete, až se doberete odpovědi.
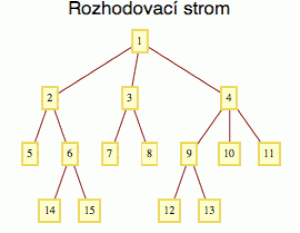
Algoritmus postupuje podobně. Sestaví si strom z otázek (viz graf vpravo) a pak si bere jeden příklad za druhým a v každém uzlu si položí nějakou otázku. Akorát se neptá, zda mají ty vektory atributů x vroubkované listy, ale dotazuje se např.: Je atribut 1 větší než atribut 3? Nebo: Je absolutní hodnota atributu 4 větší než jedna? Popřípadě u diskrétních atributů: Je atribut 5 roven 2? Podle odpovědi pak pošle příklad do nižších uzlů. A takhle protáhne každý příklad tím stromem (shora dolů, počínaje uzlem 1), až dorazí do finálního uzlu (těm se říká listy) a tam už je připravena nálepka y. Čili predikce probíhá stejně jako u rostlin sérií otázek. Odpověď je většinou binární (ANO či NE), ale není to pravidlem (např. uzel 1 a 4 na obrázku připouští tři možné odpovědi).
Otázka je, jak si počítač ten strom sestaví. Na začátku má k dispozici trénovací složku matice T, což je kupa příkladů (x,y), kde y je nálepka nabývající několika hodnot (tady těch tříd různých objektů může být více). A ty nálepky jsou ve složce nějakým způsobem rozděleny. A jak příklady probublávají stromem dolů, složka se dělí na nestejně velké podsložky a základní myšlenka je, aby se v každé podsložce koncentrovaly určité nálepky. Díky této strategii po dosažení nejspodnějšího uzlu (listu) v každé podsložce převládne určitá nálepka a tu příslušný list „zdědí“. A pokud při vlastní klasifikaci nový příklad propluje stromem právě do tohoto „listu“, dostane tu nálepku taky.
Představme si, že naše trénovací složka má 50 % příkladů s nálepkou y = 0 a 50 % s nálepkou y = 1. A řekněme, že pro první otázku (v horním uzlu) máme dvě varianty.
Varianta A. Pokud se zeptáme, zda je atribut 1 kladný, algoritmus nám pošle jednu podsložku do levé větve a druhou do pravé, ale v obou podsložkách bude rozdělení nálepek pořád zhruba fifty-fifty. Tak tudy ne.
Varianta B. Pokud se ale zeptáme, zda je třeba atribut 2 větší než 10, můžeme zjistit, že do pravé podsložky se nám dostaly příklady, kde je 80 % nálepek y = 0 a 20 % nálepek y = 1, zatímco v levé to bude naopak. Tohle je přesně, co jsme chtěli.
Je to takový Popelčin algoritmus. Na začátku má Popelka k dispozici náhodnou směsici prosa, hrachu a zrní. A po průchodu každým uzlem se směska rozdělí na podskupiny, které budou mít určité převládající nálepky. Samozřejmě v reálu máme k dispozici více variant než jen A a B (můžeme se zeptat prakticky na jakýkoliv atribut či jejich kombinaci), ale princip zůstává stejný: ze všech možných variant vybereme tu, která snižuje rovnoměrnost zastoupení nálepek ve složce (neboli zvyšuje jejich „roztříděnost“).
Jakým způsobem počítač tu roztříděnost posuzuje? Zhruba řečeno podle entropie.
Pokud máme tři nálepky (hrách, proso, čočka) a jedno jejich rozdělení je (30 %, 30 %, 40 %) a druhé (10 %, 30 %, 60 %), které z nich je roztříděnější? Když si spočítáte entropii, zjistíte, že to druhé – kde převládá třetí nálepka. A tuhle „roztříděnost“ počítač systematicky zvyšuje, aby byla v listech co nejvyšší. Jen je při výpočtu nutno přihlédnout k tomu, že složky vycházející z uzlu mají různý počet příkladů (otázka daného uzlu nemusí do každé větve nutně poslat stejný počet). Proto se ty entropie musí ještě „ovážit“ velikostmi příslušných podsložek, takže z toho nakonec vyleze veličina, které se říká „informační zisk“ (information gain).
Algoritmus má při třídění příkladů k dispozici spoustu atributů a u každého se může dotázat na spoustu vlastností (což jsou parametry této metody), takže v každém uzlu je ve hře spousta variant, jak tu roztříděnost zvyšovat. A jak asi čekáte, prakticky se to provede tak, že se pro daný výběr parametrů (tj. pro daný výběr otázek) spočítá, kolik příkladů se klasifikovalo špatně (neboť dorazily do listu, který jim přisoudil špatnou nálepku), a příslušné skóre se v parametrickém prostoru minimalizuje.
Možná si říkáte, proč prostě neudělat ten strom tak velký, že každý list bude (po dostatečně velkém počtu otázek) obsahovat pouze jeden příklad. Jeho nálepku pak zdědí všechny nové příklady do tohoto uzlu dorazivší. Takový strom by celou trénovací množinu klasifikoval přesně. De facto by se ji „nabifloval“ nazpaměť.
To ale není smyslem strojového učení. Smyslem je z trénovací množiny vytáhnout obecné trendy a zákonitosti (reprezentované funkcí F). Ne se ji naučit nazpaměť.
U testovací množiny už by tak oslnivé výsledky nebyly (mimo jiné pro to, že ona v sobě obsahuje jiné reálné vlivy ε, které se náš strom „nenašprtal“).
Sekce Jauvajs: Pohled pod kapotu
Žádný učený z nebe nespadl. Proto si učení většina lidí představuje jako poměrně komplikovaný proces probíhající v reálném čase. Proces, který je provázen celou řadou omylů a slepých uliček.
To, že do stroje naprogramujeme aritmetický průměr ve formátu (x + y)/2, samozřejmě neznamená, že se stroj něco naučil. Kde je tedy ve strojovém učení zaklíčován ten proces provázený řadou omylů a slepých uliček? Ten, zhruba řečeno, spočívá v optimalizaci.
Výše uvedenými příklady se jako červená niť vine myšlenka, že řešení dané klasifikační (či regresní) úlohy spočívá v tom, že minimalizujeme chybu v nějakém prostoru parametrů. Strojové učení se tedy realizuje hledáním minima vícerozměrné funkce F a to je proces zatížený – stejně jako lidské učení – celou řadou omylů a slepých uliček.
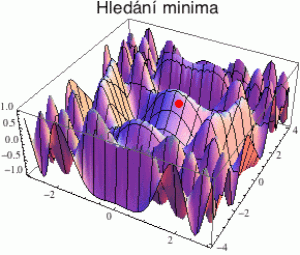
Problém spočívá v tom, že vícerozměrné funkce, se kterými se v praxi setkáme, nevypadají jako parabolické antény – kde se minimum najde raz dva – ale spíše jako bludiště hřebenů a údolíček jako na obrázku vpravo. V takovém případě je velmi snadné uvíznout u nějakého horského plesa (které je sice lokálním minimem), ale v žádném případě není minimem globálním, které hledáme (a dostat se z něho je pak docela problém).
Funkce F má obecný tvar Σchyba(p), kde p je vektor parametrů a suma probíhá přes všechny příklady obsažené v trénovací množině T.
Základní strategie hledání minima je stejná jako strategie hledání nejnižšího bodu daného údolí. Prostě vyrazíte ve směru největšího klesání – takovému směru se říká gradient funkce F a závisí pochopitelně na bodě, ve kterém se nalézáte. Zatímco v horách se ale pohybujeme spojitě a neustále svůj směr korigujeme podle povahy terénu, počítač musí rozhodnout, jak daleko se podél daného gradientu přemístí.
To je další hyperparametr, kterému se obvykle říká „vyučovací tempo“ (learning rate) a musí se opatrně vyladit. Pokud je krok příliš malý, počítač se přesunuje k minimu příliš pomalu. Pokud je moc velký, počítač může hledané minimum přeskočit a ocitnout se v úplně jiném údolí.
Obecně se této metodě říká gradientový sestup, a protože leží v samotném srdci strojového učení, má několik důležitých variant. Protože funkce F je definována jako suma chyb přes všechny příklady (a těch mohou být tisíce), počítá se gradient často postupně vždy jen pro hrstku příkladů (až do vyčerpání celé množiny T). Metodám tohoto typu (a je jich několik, podle toho, jak se ta hrstka příkladů vybírá) se v angličtině říká stochastic gradient descent. Další možností, jak určit směr dalšího postupu, je použít namísto lineární aproximace funkce (gradient je v podstatě první derivace, tedy indikátor lineárního růstu) přesnější aproximaci kvadratickou (na kterou jsou potřeba druhé derivace). Takové metody shrnuje angličtina do kategorie conjugate gradient method.
V posledních letech jsou velkým hitem strojového učení tzv. ánsámblové metody, které jsou založeny na známé lidové moudrosti, že víc hlav víc ví. Sestrojíme si několik klasifikátorů a závěrečný verdikt pak vyneseme podle jejich souhrnného doporučení. Tyto baterie učících se strojů používají pro agregaci klasifikačních výsledků jednu ze dvou základních metod:
V té první (angl. bagging) si každý klasifikátor vytvoří svůj vlastní model zcela nezávisle a výsledná nálepka je pak v podstatě výsledkem hlasování. Jedna z možností, jak si tu armádu klasifikátorů vytvořit, je vzít si stejnou architekturu (třeba rozhodovací stromy), z trénovací množiny vytvořit náhodným výběrem (s opakováním) několik menších trénovacích množin a klasifikátory pak vytrénovat na těchto náhodně vygenerovaných podmnožinách (takový přístup vede k velmi úspěšnému klasifikátoru, kterému se říká náhodný les).
Ve druhé (angl. boosting)) klasifikátory v jistém smyslu spolupracují. Můžete si je představit jako dělníky u pásu s tím, že každý klasifikátor se snaží soustředit na ty příklady, které jeho předchůdce neklasifikoval správně (to znamená, že v té chybové funkci F přiřadí těm klasifikačním „zmetkům“ větší váhu). V kategorii rozhodovacích stromů vede tato strategie k jednomu z nejpopulárnějších algoritmů posledních let, kterým je XGBoost.
Elektrikáři si rozdíly mezi oběma metodami mohou představit jako paralelní versus sériové zapojení.
Nu, pokud vás tahle změť statistiky a lineární algebry neodradila, máte docela dobré předpoklady stát se učitelem strojů. Tak vzhůru do toho. Bude to mít jednu velkou praktickou výhodu. O přestávce po vás studenti nebudou házet houbou.
Článek je redakčně upravenou verzí blogového příspěvku na serveru iDNES.cz. Publikováno s laskavým svolením autora. Další díly a původní texty jsou dostupné na blogu Jana Řeháčka.