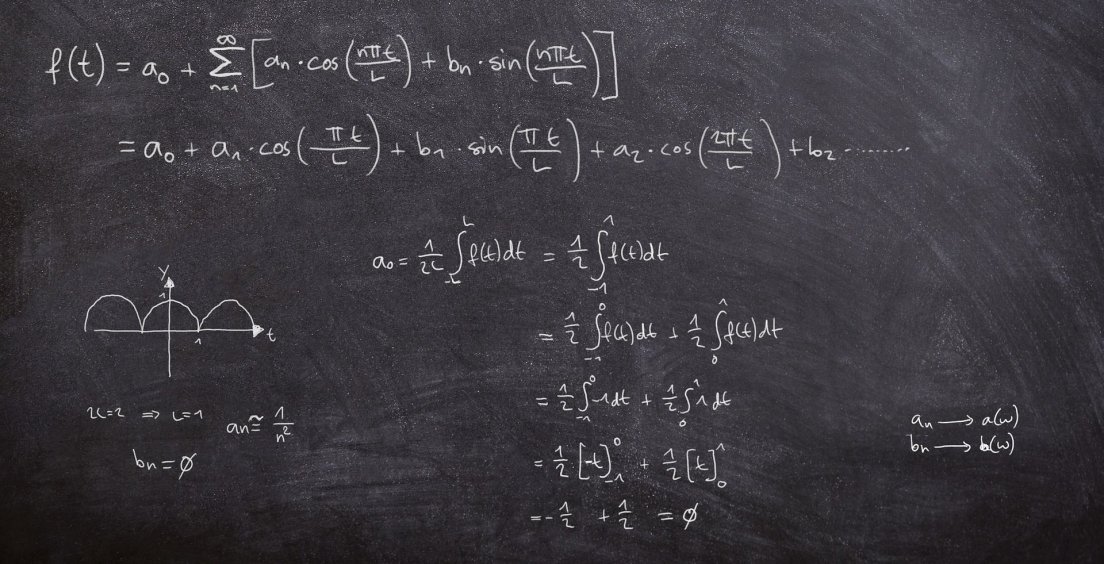Čas je jako řeka. Někdy se řítí střemhlav peřejemi vpřed (když jsme na rande) a jindy se vleče kosmickými meandry jako unavený lenochod (když čekáme na opraváře hodin). Ale ať je jeho tok rychlý nebo rozvážný, vždy plyne jen jedním směrem - od minulosti k budoucnosti. A ruku na srdce, kdo by občas nezatoužil loupnout tam zpátečku. Vrátit se o dvacet let nazpátek a napravit pár křivd, prohnat pár starých lásek a nakoupit akcie Microsoftu za babku.
Přestože nám naše zkušenost jasně říká, že čas je jednosměrná ulice, většina zákonů fyziky by proti obrácení toku času vůbec nic nenamítala. Taková slušně vychovaná diferenciální rovnice nemrkne ani okem, když se čas začne pohybovat směrem opačným.
Vezměme si třeba Newtonovy zákony. Nafilmujeme si pohyb tenisového míčku letícího přes síťku. Pustíme si ho normálně a míček letí přes síťku zprava doleva. Pustíme si ho pozpátku a míček letí zleva doprava - ale při tom dodržuje přesně ty samé zákony a dokonce si letí po té samé dráze. Když někomu oba záznamy pustíte, nebude vědět, který běží dopředu a který dozadu. Prostě obrátíte vektor rychlosti a čas valí nazpátek.
Jedna fyzikální veličina se ale časem ošálit nedá. Jmenuje se Entropie (plným jménem Entropie Vopršálková). Nalijte si do šálku kávy smetanu z mističky a nafilmujte si, jak ji mícháte. I malé děcko pozná, kdy film běží dopředu a kdy dozadu. Naše praktická zkušenost nám říká, že žádný pohyb lžičkou nám tu rozmíchanou smetanu už neodseparuje. Máma má mísu, Emma má smetanu a my máme smůlu.
(první sekce je tak trochu motivační a můžete ji přeskočit)
Shannonova entropie
(v této sekci bude lg(x) znamenat logaritmus při základu 2)
Ve 40. letech minulého století se americký matematik a elektro-inženýr Claude Shannon zabýval teoretickými aspekty přenosu informací - konkrétně do jaké míry se dá nějaká zpráva komprimovat (zhustit), aniž by došlo ke ztrátě informace. Své výsledky publikoval v roce 1948 v článku „Matematická teorie komunikace“. V něm mimo jiné definoval tzv. „informační entropii“, která dnes nese jeho jméno.
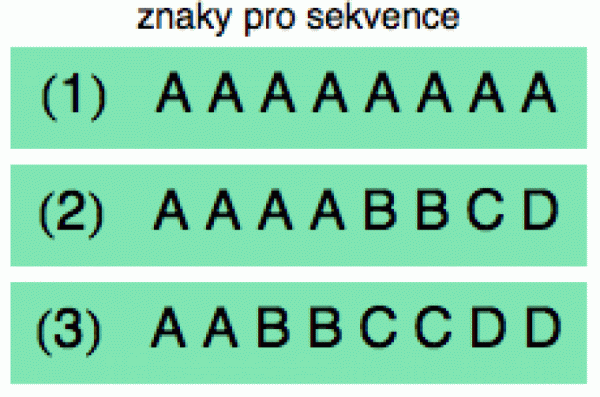
Její podstatu si můžeme ilustrovat na poměrně jednoduchém experimentu. Představme si, že máme nějaký proces, který produkuje posloupnosti 4 znaků: A, B, C a D (v dlouhodobém průměru bude každý znak x zastoupen s pravděpodobností p). Příkladem takové posloupnosti může být třeba "AACDBA". Protože prakticky celá elektronika funguje na binárním základě, pokusíme se takové posloupnosti zakódovat pomocí bitů, tedy nul a jedniček.
Nejprve se podívejme na triviální příklad, kdy si jeden znak uzurpuje všechnu pravděpodobnost pro sebe - řekněme, že to bude znak x = A. Náš proces tedy emituje áčka a nic jiného. V tomto případě se dá jakákoliv sekvence zakódovat triviálně pomocí pouhých jedniček (nebo nul - to je jedno), takže např. posloupnost "AAAA" bude zakódovaná jako "1111".
Obecně platí, že pro 4 symboly se kódovací systém, označíme ho K1, dá najít poměrně jednoduše a budou nám stačit dva bity:
(K1) A = "11", B = "10", C = "01" a D = "00"
takže například posloupnost "AACDBA" se zakóduje pomocí "111101001011".
Pokud budou znaky na výstupu zhruba stejně pravděpodobné (budou se v našich emitovaných sekvencích vyskytovat se zhruba stejnou četností), nic lepšího se v podstatě vymyslet nedá. Shannonův postřeh spočívá v tom, že pokud je v četnostech symbolů nějaká nerovnoměrnost (tedy některé symboly jsou pravděpodobnější než jiné), dá se vymyslet kompaktnější schéma.
 Abychom se o tom mohli nějak
kvantitativně bavit, představme si, že symboly vybíráme náhodně z nějakého košíku (viz obrázek). Košík (1) odpovídá situaci, kdy
máme efektivně pouze jeden symbol, tedy p = 1 pro x = A a p = 0 pro zbytek.
Košík (3) popisuje případ, kdy jsou pravděpodobnosti zhruba vyvážené
(v košíku jsou dvě verze každého písmenka), tedy p = 0.25 pro
všechny 4 znaky.
Abychom se o tom mohli nějak
kvantitativně bavit, představme si, že symboly vybíráme náhodně z nějakého košíku (viz obrázek). Košík (1) odpovídá situaci, kdy
máme efektivně pouze jeden symbol, tedy p = 1 pro x = A a p = 0 pro zbytek.
Košík (3) popisuje případ, kdy jsou pravděpodobnosti zhruba vyvážené
(v košíku jsou dvě verze každého písmenka), tedy p = 0.25 pro
všechny 4 znaky.
Nejzajímavější je košík (2), kde je symbol A nejčastější (bude se v našich sekvencích vyskytovat s pravděpodobností p = 1/2 = 0.5), symbol B bude stále poměrně běžný (najdeme ho zhruba ve čtvrtině případů p = 1/4 = 0.25) a zbývající symboly C a D budou vzácné (budou se dlouhodobě vzato vyskytovat v našich sekvencích jen asi v osmině případů p = 1/8 = 0.125).
Při analýze problému dospěl Shannon k závěru, že relativně časté symboly by se měly reprezentovat pomocí malého počtu bitů, zatímco na vzácné symboly, které v sekvenci uvidíme jen jednou za uherský rok, si můžeme dovolit vyplýtvat více bitů. Pojďme zkusit třeba tohle kódování (budu mu říkat K2 - ale ne abyste se na něj škrábali!).
(K2) A = "1", B = "01", C = "001" a D = "000"
Na posloupnost "AACDBA" nám nyní stačí pouze 11 bitů "11001000011".
Protože ale známe pravděpodobnosti všech symbolů, můžeme si udělat i odhad očekávaného počtu bitů OPB pro obecnou posloupnost, abychom se přesvědčili, že úspora nebyla specifická pro naši volbu testovací sekvence **(připomeňme si, že očekávanou neboli střední hodnotu nějaké náhodné proměnné, zde počet bitů, dostaneme tak, že vynásobíme všechny hodnoty jejich pravděpodobnostmi a pak to celé sečteme - viz toto Matykání. Bitové délky pro jednotlivé znaky odečteme z kódování a jejich pravděpodobnosti jsou uvedeny nad nimi. Takže dostaneme:
OPB = 0.5 * 1 + 0.25 * 2 + 0.125 * 3 + 0.125 * 3 = 1.75 (bitů na znak)
Kódování K2 je tedy v dlouhodobém průměru skutečně úspornější než to obecné K1 - ale pouze pro košík (2). Pokud je posloupnost generovaná z košíku (3), tak nám K2 dá horší výsledek:
OPB = 0.25 * 1 + 0.25 * 2 + 0.25 * 3 + 0.25 * 3 = 2.25 (bitů na znak)
Shannon si položil otázku jak hluboko se - pro dané rozdělení znaků - dá OPB stlačit. Nejprve si zopakujme, že B bitů nám umožní zakódovat až N=2^B znaků. Konkrétně
1 bit umí zakódovat 2 znaky (0 = "A", 1 = "B")
2 bity zakódují až 2² = 4 znaky (viz kódování K1 výše)
3 bity zakódují až 2³ = 8 znaků atd... (a 0 bitů nám v jistém smyslu umožňuje zakódovat pouze 1 znak)
A obráceně: pro N znaků budeme potřebovat plus minus B = lg(N) bitů.
Pokud se tedy daný znak vyskytuje s pravděpodobností p = 1/N (tedy zhruba každý N-tý znak), měli bychom na jeho zakódování spotřebovat zhruba B = lg(N) = lg(1/p) znaků. Čím menší pravděpodobnost, tím více bitů budeme ochotni vyplýtvat. Sečtením přes všechny hodnoty p získáme konečný odhad pro střední hodnotu:
H = Σ pi * lg(1/pi) = - Σ pi * lg(pi) = -p1 * lg(p1) - p2 * lg(p2) - ... -
pn * lg(pn)
(kde pi je pravděpodobnost i-tého znaku xi)
A to je slavná Shannonova informační entropie. Pro dané rozdělení znaků zadané hodnotami pi nám ukazuje nejmenší hodnotu, na jakou se dá stlačit zakódování typické posloupnosti, aniž by došlo ke ztrátě informace: tedy H <= OBP.
Můžete si spočítat, že pro košík (2), ve kterém jsou 4 hodnoty s pravděpodobnostmi (1/2, 1/4, 1/8, 1/8), skutečně dostanete H = 1.75 (jak lze očekávat). Pro košík (3) vám vyjde H = 2.0 a v košíku (1) je H = 0 (tam není potřeba kódovat vůbec).
Technická poznámka: Pokud je některá z pravděpodobností rovna 0, příslušný člen v daném součtu, tedy p*ln(p), bude také roven nule. To zní trochu jako zločin, protože logaritmus v nule není definován, ale protože výraz p*ln(p) se limitně blíží k nule (pokud se p blíží k nule), dá se to skousnout.
(tuto podsekci možno přeskočit)
V rámci zjednodušení jsem si trochu zafixloval. Vztah B = lg(N) platí jen pro rovnoměrné rozdělení znaků (a to se ještě musí leccos zamést pod koberec). Shannon to musel udělat trochu jinak. Máme-li posloupnost m znaků (x1, x2, ..., xm), vybraných z nějakého košíku s n typy znaků (z nichž každý má pravděpodobnost pi), pak celková pravděpodobnost této sekvence bude vyjádřena takto (zde používám symbol ∏ pro součin):
p(x1,x2,...,xm) = p(x1) * p(x2) * ... * p(xm) = ∏ p(xi)
Mnohé znaky xi se opakují, takže jejich pravděpodobnosti je možno sdružit: pokud si označíme frekvence jednotlivých znaků jako f1, f2, ..., fn, tak dostaneme:
p(x1,x2,...,xm) = ∏ pi^fi
(a ten součin vpravo už běží jen přes jednotlivé typy znaků, tedy od
1 do n)
Protože frekvence fi se dají odhadnout z pravděpodobnosti jednotlivých znaků: fi~m*pi, dostaneme vyjádření, ve kterém už nalezneme entropii H:
p(x1, x2, ..., xm) = ∏ (pi^pi)^m = ∏ exp(pi*log(pi))^m = exp(-mH)
Tímto způsobem Shannon odhadl pravděpodobnost posloupnosti znaků vybraných z daného rozdělení pomocí entropie tohoto rozdělení. To samozřejmě ještě není důkaz, že H nám ukazuje délku toho optimálního zakódování. Na to musel Shannon nejprve zavést pojem „typické“ posloupnosti, jejíž znaky poměrně přesně kopírují uvažované rozdělení, a potom odhadnout jejich počet. To už je poměrně technická záležitost a můžete si ji prostudovat v jeho původním článku.
 Komu to odvození přes
kódování do bitů není moc po chuti, může si tu entropii představit
jinak. Předpokládejme, že přístroj nám opět vyhazuje na výstupu
posloupnost znaků, a zamysleme se nad tím, jaký je minimální počet
binárních otázek (typu ANO/NE), které budeme v průměru potřebovat na
určení toho kterého znaku.
Komu to odvození přes
kódování do bitů není moc po chuti, může si tu entropii představit
jinak. Předpokládejme, že přístroj nám opět vyhazuje na výstupu
posloupnost znaků, a zamysleme se nad tím, jaký je minimální počet
binárních otázek (typu ANO/NE), které budeme v průměru potřebovat na
určení toho kterého znaku.
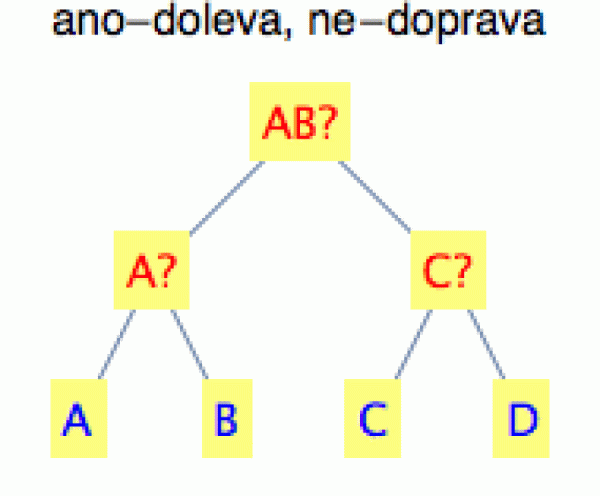
U košíku (3) je to jasné. Musíme položit dvě otázky (jak ukazuje obrázek vpravo). Nejprve se zeptáme, zda je to jeden ze znaků AB, a v druhém kole to doladíme.
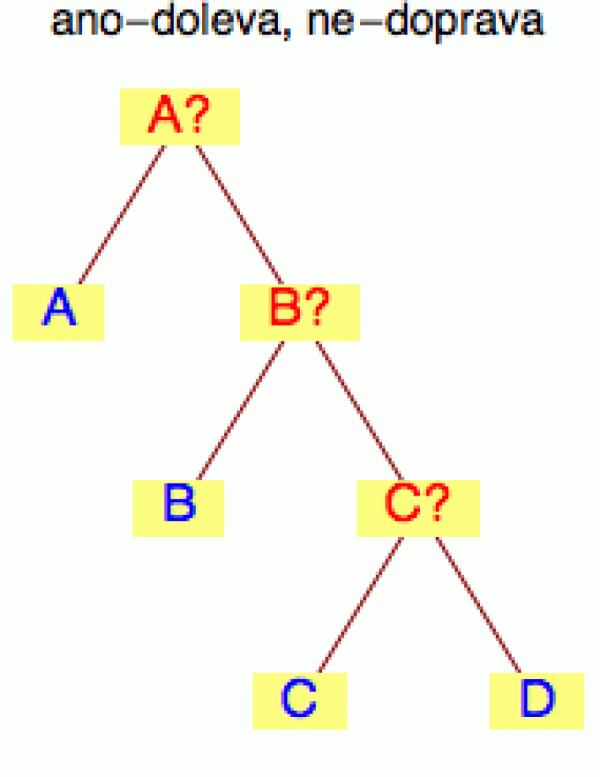 Pokud ale vybíráme z košíku (2), kde dominuje znak A, bude pro nás výhodnější ptát se nejprve
na znak A (to je nejpravděpodobnější možnost, takže poměrně často
ten znak uhodneme hned napoprvé), pak zda je to B a nakonec C. Tím sice
na znaky C a D spotřebujeme 3 otázky (stejně jako nahoře jsme na ně
vyplýtvali 3 bity), ale protože tyto znaky jsou poměrně vzácné, když
začneme počítat tu střední hodnotu (tedy de facto časový
průměr), výsledně na tom ušetříme.
Pokud ale vybíráme z košíku (2), kde dominuje znak A, bude pro nás výhodnější ptát se nejprve
na znak A (to je nejpravděpodobnější možnost, takže poměrně často
ten znak uhodneme hned napoprvé), pak zda je to B a nakonec C. Tím sice
na znaky C a D spotřebujeme 3 otázky (stejně jako nahoře jsme na ně
vyplýtvali 3 bity), ale protože tyto znaky jsou poměrně vzácné, když
začneme počítat tu střední hodnotu (tedy de facto časový
průměr), výsledně na tom ušetříme.
Entropie H se tedy dá nahlížet jako minimální počet otázek, které v průměru potřebujeme k určení znaků generovaných z daného rozdělení. To kódování pomocí bitů vlastně není nic jiného než symbolický záznam našich odpovědí: 1 = ano, 0 = ne.
Na vzoreček pro entropii H se můžeme také dívat takto. Výraz lg(1/p) představuje určitý moment překvapení, který každá hodnota xi (zde znak) představuje. Čím menší pravděpodobnost, tím větší překvapení, a tedy tím více informace. Pokud vám někdo na Sahaře předpoví, že zítra bude svítit slunce, bude pravděpodobnost vysoká (p ~ 1), ale moment překvapení (a tedy reálná informace, kterou získáváme) bude prakticky nula. Zato předpověď prudké bouřky nám podává zcela zásadní informaci, protože je nečekaná (p << 1). Na střední hodnotu těchto „momentů překvapení“ (což je Shannonova entropie) se tedy můžeme dívat jako na „průměrný informační obsah“, který daná sekvence nese.
Ten první košík negeneruje žádnou informaci, protože přesně víme, co nás čeká. Druhý už nám jakous takous informaci podává, a maximální informace přichází z košíku (3), kde je každý nový znak prakticky nepředvídatelný.
Když Shannon svou entropii odvodil, měl nejprve v úmyslu hodnotu H nazvat „informace“, ale protože mu to slovo připadlo v oboru už příliš zprofanované, uvažoval o „neurčitosti“. Z jeho dilematu ho nakonec vysvobodil další známý matematik John von Neumann, který mu poradil: Měl bys tomu říkat „entropie“ ze dvou důvodů. Za prvé, ta tvoje funkce neurčitosti už se pod tímto jménem používá ve statistické fyzice, takže jméno vlastně má. Za druhé, a to je důležitější, nikdo ve skutečnosti neví, co to entropie opravdu je, a tak budeš mít v debatách vždycky výhodu.
Myslím, že fyzici mu tuto uštěpačnou poznámku nikdy neodpustili.
Statistická entropie
(v této sekci bude ln(x) znamenat logaritmus při základu e)
Entropie H, kterou Claude Shannon definoval v souvislosti s kódováním posloupností, se dá aplikovat na libovolné diskrétní rozdělení a popisuje jeho míru nahodilosti, neuspořádanosti či chcete-li chaotičnosti.
(ona se dá definovat i pro spojitá rozdělení, ale jednak není úplně košer a jednak se tam místo sčítání musí integrovat, takže takovou si mlsku pro tentokrát odpustíme).
Pro diskrétní náhodnou veličinu X, která nabývá n různých hodnot xi s pravděpodobnostmi P = (p1, p2, ..., pn) definujeme entropii H stejně jako Shannon:
H(P) = Σ pi * ln(1/pi) = - Σ pi * ln(pi)
Všimněte si, že hodnoty xi v této formulce vůbec nefigurují. Entropii ovlivňuje pouze rozdělení pravděpodobností mezi tyto hodnoty - zda xi reprezentují počty aut na dálnici, vítězství fotbalových týmů nebo ekonomické ukazatele, je vcelku jedno. Čím rovnoměrněji je pravděpodobnost rozdělena, tím vyšší entropie.
Nejprve se podívejme na jeden speciální případ. Pokud je všechna pravděpodobnost soustředěna v jedné hodnotě, tedy např. P = (1, 0, ..., 0), pak její entropie bude H(P) = 0. To není nic překvapivého, protože taková veličina de facto náhodná vůbec není - každá její realizace nám na výstupu vyhodí první hodnotu s pravděpodobností 100 %. Entropie, jako míra nahodilosti, tuto skutečnost přirozeně reflektuje (a stejně jako v předchozí sekci uvažujeme limitně: 0*ln(0)=0).
Dalším zajímavým extrémem je situace, kdy má všech n hodnot přesně stejnou pravděpodobnost. Rozdělení je pak uniformní, kolekce pravděpodobností je P = (1/n, 1/n, ..., 1/n) a dosazením do vzorečku zjistíme, že entropie je v tomto případě rovna H(P) = ln(n). A protože pro každou veličinu s n hodnotami entropie splňuje nerovnici
H(P) <= ln(n)
je jasné, že uniformní rozdělení nabývá maximální možnou entropii. Tento fundamentální vztah vyplývá z tzv. Jensenovy nerovnosti a podíváme se na něj v dnešní sekci Jauvajs.
Na dalším obrázku vidíme tři různá rozdělení pro náhodnou veličinu nabývající n = 20 různých hodnot, jejichž pravděpodobnosti odpovídají výšce každého sloupečku. Entropie je vyznačena v záhlaví a zleva doprava stoupá. Rozdělení vpravo je téměř deterministické, náhodná veličina nabývá s velkou pravděpodobností hodnoty 7 (zatímco ty ostatní jsou zastoupeny jen „stopově“). Rozdělení vlevo je téměř dokonale nahodilé (takto vypadá např. rozdělení loterijních čísel) a jeho entropie se blíží maximální možné hodnotě. Pro rozdělení, které nabývá n = 20 možných hodnot, je maximální možná entropie ln(20) = 2,996.
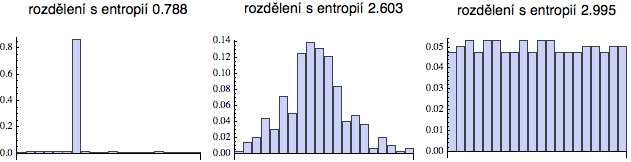
Entropie tedy ukazuje, kolik nahodilosti můžeme při generování dané náhodné veličiny očekávat. Největší je pro ta rozdělení, která své hodnoty produkují chaoticky a s prakticky stejnou pravděpodobností. Jakmile se v náhodné veličině začne objevovat nějaký řád - tedy jisté hodnoty se začnou objevovat častěji než jiné (viz uprostřed), pak její entropie začne klesat a pokud nějaká hodnota nakonec „zvítězí“ a všechny ostatní hodnoty z náhodné veličiny „vytlačí“, entropie klesne na nulu.
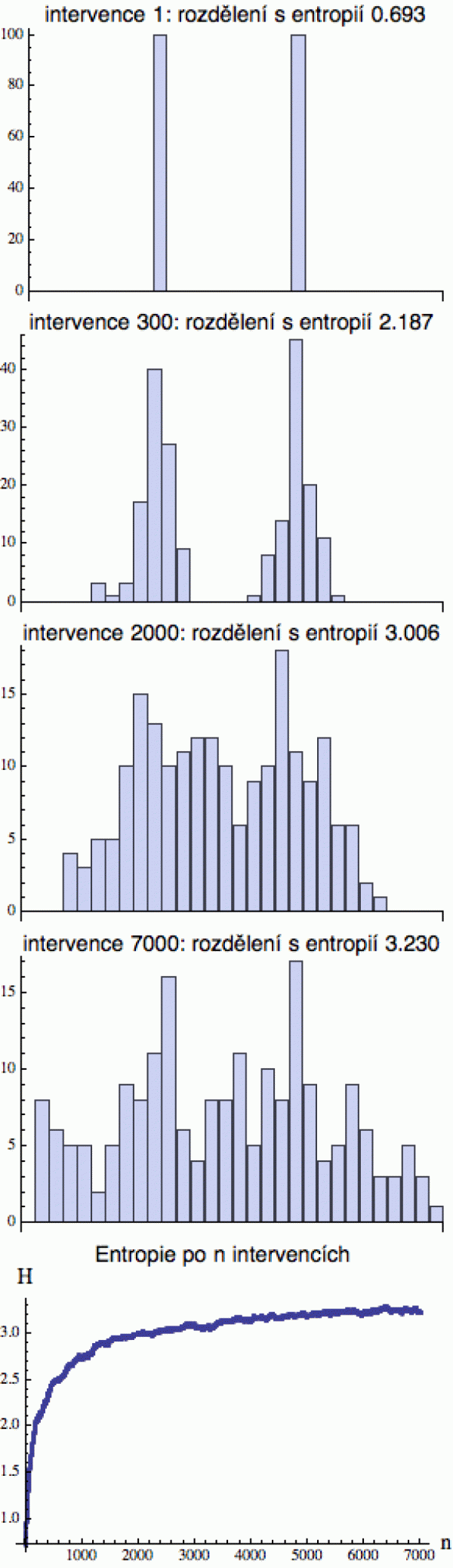 Abychom viděli, co má entropie společného s tokem
času, uděláme si takový malý hokus pokus. Začneme s binárním
rozdělením (viz horní obrázek vpravo), které si představíme jako
dva sloupce se 100 kuličkami. Dohromady je podél osy x připraveno 30
sloupců, které jsou všechny prázdné (až na sloupce č. 10 a 20).
Abychom viděli, co má entropie společného s tokem
času, uděláme si takový malý hokus pokus. Začneme s binárním
rozdělením (viz horní obrázek vpravo), které si představíme jako
dva sloupce se 100 kuličkami. Dohromady je podél osy x připraveno 30
sloupců, které jsou všechny prázdné (až na sloupce č. 10 a 20).
A teď si pozveme zlomyslného démona, budu mu říkat Bubu, a ten si náhodně vytáhne jednu kuličku. Pak si hodí korunou a padne-li panna, přidá ji do sousedního sloupce vlevo, a padne-li orel, umístí ji do sousedního sloupce vpravo. Tomuto procesu budu říkat intervence.
To znamená, že při druhém tahání bude Bubu vybírat z náhodné veličiny, která je trochu jiná - přehození kuličky z jednoho sloupce do druhého přenastaví pravděpodobnosti (sloupec, ze kterého kuličku vybral, bude v dalším tahu o trochu méně pravděpodobný a ten, do kterého ji vhodil, bude naopak více pravděpodobný).
Druhá intervence proběhne stejně. Bubu si opět náhodně vybere kuličku a hodí ji do jednoho ze sousedních sloupců, podle toho jak mu padne koruna. A takhle se to opakuje pořád dokola. Viz série obrázků, která ukazuje počty kuliček po dané intervenci. Ten proces trochu připomíná difúzi - jeden z důležitých mechanismů pro nárůst entropie.
Protože vyšší sloupce mají více kuliček a tudíž vyšší pravděpodobnost, že se stanou "obětí" ztráty kuličky, sloupce se postupně zarovnávají a entropie působením démona utěšeně roste (to je nejlépe vidět na tom spodním souhrnném obrázku).
Pozor - neplést s Maxwellovým démonem, který v jistém smyslu funguje opačně (entropii systematicky zmenšuje). A taky se nejmenuje Bubu, ale James Clerk.
A jak to souvisí s časem? Představte si, že vám ukážu jen ten druhý a čtvrtý obrázek, a zeptám se vás, který předcházel kterému. Většina lidí ten nárůst entropie intuitivně vycítí: druhý obrázek musí časově předcházet čtvrtému. Zub času struktury nevytváří, ale rozkousává. Je krajně nepravděpodobné, že byste vystartovali s nějakým jakž takž rovnoměrným rozdělením (čtvrtý obrázek) a náhodným přehazováním v něm začali vytvářet „eiffelovky“ (druhý obrázek).
Náhoda obecně postupuje od uspořádaných struktur k neuspořádaným a Shannonova entropie dokáže tuto její libůstku zachytit.
Když se ale na tu entropickou křivku pozorně podíváte, zjistíte, že nestoupá úplně monotónně. Občas se stane, že Bubu vytáhne kuličku z „nižšího“, méně pravděpodobného sloupku a hodí ji do sousedního, který může být o něco vyšší (tím se entropie dočasně sníží). V dlouhodobém horizontu ale zvítězí neuspořádanost.
Tento experiment je vlastně takový plastikový model druhého zákona termodynamiky, který říká, že entropie izolovaných systémů s časem neklesá. Mimochodem, také tento zákon je nutno chápat statisticky (tedy v průměru). Fyzikové zjistili, že i termodynamická entropie může (pro dostatečně malé systémy) dočasně klesnout. Ale opravdu jen na chvilku.
Nárůst entropie samozřejmě vybízí k filosofické otázce - pokud má termodynamika takový zálusk na neuspořádanost, odkud se vzaly všechny ty báječné uspořádané struktury, které kolem sebe vidíme? Současná fyzika má za to, že za nimi stojí velký třesk, tedy velmi uspořádaný stav s extrémně nízkou entropií. Kdo ale vesmír do takového stavu uvedl? Metavesmír s jinými zákony, kde mohou vznikat nízko-entropické objekty, a nebo nějaký ten šikovný Stvořitel? Tuto otázku si musí každý čtenář zodpovědět sám ve své vlastní hlavě (já osobně si myslím, že za tím stojí Tlahuizcalpantecuhtli ,ale nechci tento názor nikomu vnucovat).
A k čemu je ta statistická entropie dobrá? V první řadě je to důležitá vlastnost každého rozdělení, která se hodí, pokud je nutno posoudit, kdy je jedno nahodilejší než druhé. Anebo pokud potřebujete svá data roztřídit podle rovnoměrnosti: například při posuzování všestrannosti ekonomik - některé země mají ekonomické aktivity poměrně vyvážené a rozdělené do mnoha sektorů, zatímco jiné se soustřeďují jen na jedno nebo dvě odvětví a v ostatních se výrazně neangažují. Entropie to dokáže kvantifikovat.
Minule jsme také viděli, že často je potřeba odhadnout, jak moc podobné si dvě různá rozdělení jsou. K tomuto účelu se často používá tzv. křížová entropie (cross entropy).
H(P,Q) = Σ pi ln(1/qi)
Pokud se na člen ln(1/q) budeme dívat jako na „míru překvapení“ (viz dnešní první sekce) generovanou rozdělením Q, ale zprůměrovanou rozdělením P, dostaneme trochu jiné číslo, než kdybychom tu „míru překvapení“ zprůměrovali podle jejích vlastních hodnot Q. A tato malá diference je základem jedné z nejúspěšnějších metrik v moderní datové analýze: Kullback-Leiblerova divergence (viz sekce Jauvajs v minulém díle) není nic jiného než rozdíl křížové entropie a entropie původní.
KL(P,Q) = H(P,Q) - H(P)
Navíc se ukázalo, že křížová entropie je sama o sobě výborným ukazatelem pro míru odchylky mezi modelem a skutečností (tzv. ztrátová funkce) při strojové klasifikaci. Sofistikované programy, které si naládují obrázek do paměti a samy poznají, zda je to kůň, kočka nebo hroch, používají ke kalibraci právě křížovou entropii (kde náhodnou veličinou jsou hodnoty pixelů). K tomu se časem vrátím, ale pokud to někoho enormně zajímá, může se mrknout sem.
Další důležitou oblastí automatického zpracování dat jsou tzv. rozhodovací stromy. Ty jsou tvořeny sérií otázek, posunujících jednotlivá data „stromem“ do výsledné destinace, kde jsou opatřeny nějakou nálepkou (klasifikací do nějaké kategorie). Je to podobný proces jako „hádání znaku“ z předešlé sekce.
Při automatické tvorbě takových stromů (tedy při návrhu jejich struktury) se samozřejmě snažíme, aby první otázky dokázaly celý soubor datových objektů co nejvíce a nejpravidelněji „nadrobit“. Strom, který v první otázce rozhodí 400 datových objektů na 397 a 3, asi moc efektivní nebude. A k tomu pravidelnému „drobení“ se právě používá entropie (přesněji informační zisk, který je na ní založen).
A konečně důležitou roli ve statistické analýze hraje také tzv. princip maximální entropie, který říká, že pokud neznáme hledané rozdělení přesně, ale zatím známe pouze některé jeho vlastnosti, pak ze všech možných rozdělení, která reprezentují momentální stav našich vědomostí o datovém souboru je nejlepší volbou to, které má maximální entropii. Je tedy co nejrovnoměrněji rozložené (při zachování podmínek, které jsme z dat zatím vyčetli). V jistém smyslu je tento princip statistickou verzí slavné Occamovy břitvy.
Boltzmannova entropie
I ve fyzice má entropie statistickou povahu a projevuje se při pozorování systémů, skládajících se z velkého množství objektů (obvykle částic).
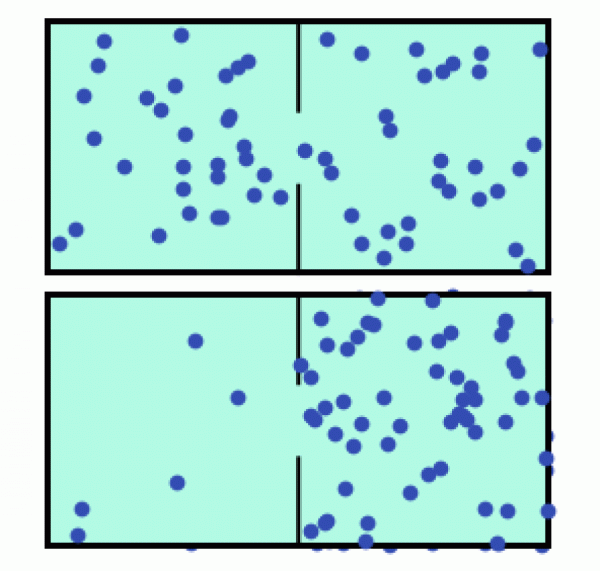 Do dvou částečně
oddělených komor vypustíme plyn a budeme zkoumat jeho rozložení. V drtivé
většině případů nalezneme plyn v režimu, kdy bude částic v obou
komorách plus minus stejně (viz horní část obrázku). Opačná
situace, kdy by se většina částic shodou okolností ocitla v pravé komoře,
je sice fyzikálně možná, ale krajně nepravděpodobná.
Do dvou částečně
oddělených komor vypustíme plyn a budeme zkoumat jeho rozložení. V drtivé
většině případů nalezneme plyn v režimu, kdy bude částic v obou
komorách plus minus stejně (viz horní část obrázku). Opačná
situace, kdy by se většina částic shodou okolností ocitla v pravé komoře,
je sice fyzikálně možná, ale krajně nepravděpodobná.
To, co jim zabraňuje ve shlukování, je entropie (to ona obchází komorou jako policajt a volá „rozejděte se!“). Její nejjednodušší forma náleží Boltzmannovi a je založena na pojmu mikrostavu a makrostavu.
Plyn se skládá z velkého množství atomů, které si jen tak nazdařbůh poletují vymezeným prostorem. Díky četným srážkám je prakticky nemožné přesně spočítat jejich polohu a rychlost, tedy určit jejich mikrostav (představu, jak moc částic plyny obsahují, poskytuje Avogadrovo číslo - výpočet tolika parametrů by i na nejmodernějších superpočítačích trval celá staletí). Proto se fyzikové při popisu takových systémů zaměřují na makroskopicky měřitelné vlastnosti, jako je tlak, teplota, objem atd.
Boltzmannova entropie je definována jako logaritmus počtu mikrostavů odpovídajících danému makrostavu: S = k*ln(W), kde W je počet mikrostavů a k je Boltzmannova konstanta, odrážející volbu jednotek (pro naše účely bude k = 1). Abychom ale nezabředli příliš hluboko do statistické mechaniky, uděláme si takový zjednodušený pokus.
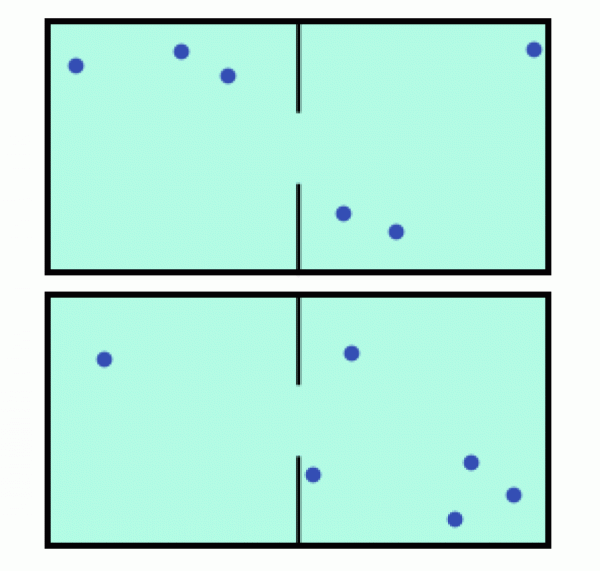 Do polo-oddělené komory
vypustíme několik částic, které si pojmenujeme - jako by to byly ovce na
farmě pasoucí se tu v levé, tu v pravé části pastviny. Mikrostavem bude
konkrétní konfigurace částic/ovcí, např. Alžběta, Barbora a Cindy v pravé části, versus Dana, Eliška a Felicie v levé (horní
obrázek). Makrostavem budou pouze souhrnné počty částic/ovcí v obou
podkomorách bez znalosti toho, která je která. Mikrostav je tedy to, co vidí
bača (který ovce zná), makrostav je to, co vidí náhodný turista
(tři ovce tady a tři tam).
Do polo-oddělené komory
vypustíme několik částic, které si pojmenujeme - jako by to byly ovce na
farmě pasoucí se tu v levé, tu v pravé části pastviny. Mikrostavem bude
konkrétní konfigurace částic/ovcí, např. Alžběta, Barbora a Cindy v pravé části, versus Dana, Eliška a Felicie v levé (horní
obrázek). Makrostavem budou pouze souhrnné počty částic/ovcí v obou
podkomorách bez znalosti toho, která je která. Mikrostav je tedy to, co vidí
bača (který ovce zná), makrostav je to, co vidí náhodný turista
(tři ovce tady a tři tam).
Každý makrostav obvykle odpovídá několika možným mikrostavům. Například makrostav 3:3 na horním obrázku může být způsoben tím, že v pravé části pastviny je Alžběta, Dana a Felicie, nebo Barbora, Cindy a Dana, anebo jakákoliv jiná trojice ovcí - a takových možností je spousta. Pro konfiguraci 1:5 na spodním obrázku už je možností daleko méně.
Pojďme si to spočítat. Pro makrostav odpovídající rozložení 0:6 existuje jediný mikrostav - všechny ovce jsou vpravo, žádná vlevo. Jeho Boltzmannova entropie tedy bude 0 = ln(1). Makrostav 1:5 už se dá realizovat šesti mikrostavy (spodní obrázek) - vpravo je jedna z šesti ovcí a vlevo zbytek. Entropie tedy bude ln(6) = 1,792. U makrostavu 3:3 se vlevo může objevit libovolná trojice ovcí a jejich počet je dán binomickým koeficientem B(6,3) = 20 (to odpovídá entropii ln(20) = 2,996). Rovnoměrné makrostavy mají tedy více možností se realizovat, a tudíž mají větší entropii. B(6,3) je to samé jako „šest nad trojkou“
Pro několik málo částic se ten rozdíl nezdá být velký, ale jakmile si jich vezmete na paškál více, rozdíly budou markantní. Pro 100 částic/ovcí (a to není z pohledu termodynamiky žádné omračující číslo) bude počet mikrostavů pro makrostav 1:99 pochopitelně roven 100 (v levé části se postupně vystřídají všechny ovce, vpravo je zbytek). Pro vyrovnaný makrostav 50:50 už ale dostaneme obrovské množství možných realizací, protože binomické číslo, udávající kolika způsoby lze vybrat 50 ovcí ze 100, je B(100,50) = 100,891,344,545,564,193,334,812,497,256.
Proti tomuto velečíslu je 100 jako plivnutí v moři. A teď si představte, že těch částic/ovcí není sto, ale Avogadrovo číslo (no to už by ten plyn musel bejt vyloženě ultra záludnej, aby se nasáčkoval do jedný komůrky). Matička příroda nemá žádné favorizované stavy, ale vybírá si mezi nimi náhodně. Ty rovnoměrné s velkou entropií mají proto drtivě vyšší šanci na realizaci (jako když si koupíte víc losů, tak máte větší šanci na výhru).
Růst entropie s časem - tedy přechod od méně pravděpodobných stavů k těm pravděpodobnějším - je v zásadě statistickým mechanismem. Jakým způsobem systém mezi různými stavy hopsá, je pak otázkou příslušné dynamiky a z matematického pohledu se tímto problémem zabývá tzv. ergodická teorie.
Mimochodem, ten samý mechanismus jsme viděli v druhém Matykání této série, ve kterém jsme pozorovali, jak vyrovnaný je hod korunou. Zatímco pro malý počet hodů, řekněme deset, se vám lehko může stát, že hodíte 4 panny a 6 orlů, u milionu hodů je prakticky vyloučené (i když teoreticky možné), že hodíte 400 000 panen a 600 000 orlů. A s entropií je to zrovna tak. Čím více složek daný systém má, tím menší je pravděpodobnost, že dojde k odchylkám od statistického normálu. Proto se nemusíte bát, že byste se v noci udusili, protože se všechny molekuly kyslíku rozhodly shromáždit pod postelí. Entropie Vopršálková a Avogadrovo číslo jim to nedovolí.
Zajímavou otázkou je, jak fyzikální entropie souvisí s tou informační (statistickou). Na první pohled se zdá, že v obou případech je entropie vyjádřením určité rovnoměrnosti rozdělení (či nedostatku vnitřní struktury). Ta Boltzmannova je ale poměrně speciální pojem, který funguje jen za specifických fyzikálních podmínek (všechny mikrostavy jsou stejně pravděpodobné). Obecnější formou je entropie Gibbsova, která mikrostavům s pravděpodobnostmi pi přiřazuje hodnotu
S = k Σ pi*ln(pi)
což je vzoreček formálně shodný s tím Shannonovým.
Zda to ale znamená, že Gibbsova a Shannonova entropie spolu nějak významně souvisí, je trochu oříšek, ohledně kterého - jak se zdá - nepanuje úplná shoda. Proto do toho nebudu moc šťourat a odkážu vás na wikipedii (anebo sem).
Literární shrnutí: Krvavý Džejk seděl na pohovce domu nevalné pověsti a obdivoval pořádek i vytříbený vkus Madamme Fifi. Stříbrné karafy pózovaly v policích jako vojáci nastoupení k přehlídce, ze stěn shlížely starodávné obrazy divočiny a sametové polštáře na divanu byly rozloženy téměř s geometrickou pravidelností. Za městečkem byla objevena velká ložiska mědi a na nedostatek zákazníků si v tomto zařízení nikdo stěžovat nemohl. Lítacími dveřmi se do předsálí vpotácel důlní inženýr Wágner s otevřenou lahví whiskey v jedné a nabitým koltem v druhé ruce. Jedním rozpřáhnutím ruky srazil z poličky tu nejdražší karafu a svým koltem rozstřílel dobrou polovinu polštářů. Při tom rozšafně kopal do všeho, co se mu připletlo do cesty, a hulákal jako na lesy. Ovšem nezpíval si „Das ist nur die Erste Phaaase“, jak by se leckterý cimrmanolog mohli domnívati, ale bavorskou verzi písně „Oh my darling Clementine“. Když se chraplavě pustil do druhé sloky, na schodišti se objevila rozčepýřená Madamme Fifi a spráskla ruce: „Vy bezbožný kojote, co to tu provádíte?“ Inženýr Wágner na okamžik ztuhl, svůj doběla rozpálený kolt se pokusil zastrčit do pouzdra a rozleptaným jazykem opilců ze sebe vysoukal: „Já vám tu zvyšuju entropii, paninko.“ Ruská imigrantka Tamara, sedící v koutku, zastříhala zvědavě ušima: „I u vas jesť kakoj nibuď entropyj?“ Ale nikdo neodpověděl a její slova se rozplynula do stydlivého ticha. „To že řekla?“, mohl by si pomyslet již zmíněný leckterý cimrmanolog, ale Džejk se jen pod vousy světácky pousmál a se zájmem pozoroval, jak se rozparáděný Wágner chopil rozprašovače na voňavku a opakovaným stlačením tlakového balonku pokračoval ve zvyšování entropie. „Diese maschine ist diffuseur,“ mohl by do třetice všeho dobrého konstatovat všudypřítomný cimrmanolog, ale Madamme Fifi neměla žádné pochopení pro efektivnost průmyslové parfumerie. Jen si dala ruce v bok a nespokojeně zahudrovala: „Není žádná spravedlnost na tom světě - zlatokopům každý půlrok zvyšují platy, ale bordelu nikdo nepřidá!“
Sekce jauvajs: Jensenova nerovnost
(jen pro mimořádně otrlé povahy)
Jensenova nerovnost je důležitým zdrojem nerovnic v matematice.
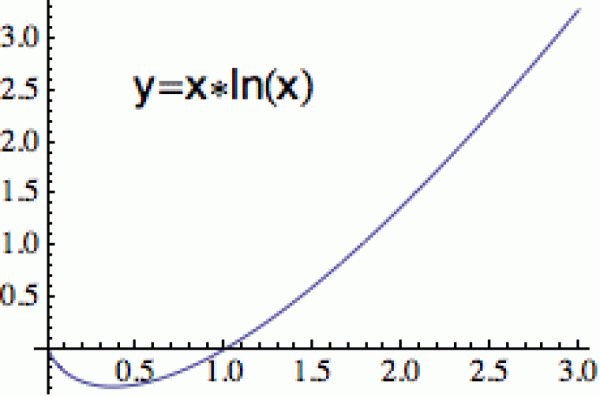 Dotýká se konvexních objektů.
Konvexní jsou technicky vzato ty funkce, jejichž graf leží nad každou
tečnou (ještě techničtěji: mají rostoucí derivaci), ale
neformálně si je můžete představit tak, že z jejich grafu nevyteče voda,
pokud do něj naprší (viz obrázek). Berte to ale jen jako hrubou
představu (např. funkce 1/x je konvexní pro kladná x a dešťovka by z toho grafu v pohodě odtekla).
Dotýká se konvexních objektů.
Konvexní jsou technicky vzato ty funkce, jejichž graf leží nad každou
tečnou (ještě techničtěji: mají rostoucí derivaci), ale
neformálně si je můžete představit tak, že z jejich grafu nevyteče voda,
pokud do něj naprší (viz obrázek). Berte to ale jen jako hrubou
představu (např. funkce 1/x je konvexní pro kladná x a dešťovka by z toho grafu v pohodě odtekla).
Funkce x*ln(x) patří mezi konvexní. Druhou důležitou ingrediencí je "konvexní kombinace": https://en.wikipedia.org/wiki/Convex_combination. My ji budeme potřebovat jen pro čísla, ale dá se definovat i pro vektory (a v tom případě úzce souvisí s tzv. barycentrickými souřadnicemi).
Konvexní kombinací dvou reálných čísel x a x' je výraz X = t * x + ť * x', kde t + t' = 1. Protože v tomto případě je konvexní kombinace plně určena parametrem t, často ji vidíte zapsanou jako X = t * x + (1-t) * x'. Pokud parametr t měníme spojitě od 1 k 0, pak bod X spojitě přejde od x k x'.
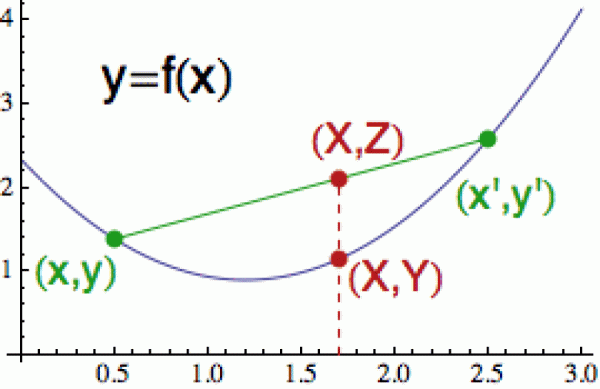 Jensenova nerovnost v tomto
případě říká, že když povedeme sečnu dvěma body konvexní funkce,
x a x', tak funkční hodnoty mezi těmito
body budou vždy POD sečnou (viz obrázek). To znamená, že když si
vybereme nějaký vnitřní bod X (tedy konvexní kombinaci hodnot
x a x'), bude platit, že funkční
hodnota Y = f(X) bude menší než příslušná hodnota Z na sečně. Vzhledem k tomu, že hodnota Z je odpovídající konvexní kombinací hodnot y a y',
můžeme nerovnost zapsat ve tvaru:
Jensenova nerovnost v tomto
případě říká, že když povedeme sečnu dvěma body konvexní funkce,
x a x', tak funkční hodnoty mezi těmito
body budou vždy POD sečnou (viz obrázek). To znamená, že když si
vybereme nějaký vnitřní bod X (tedy konvexní kombinaci hodnot
x a x'), bude platit, že funkční
hodnota Y = f(X) bude menší než příslušná hodnota Z na sečně. Vzhledem k tomu, že hodnota Z je odpovídající konvexní kombinací hodnot y a y',
můžeme nerovnost zapsat ve tvaru:
Y = f(X) = f(tx + t'x') <= ty + t'y' = tf(x) + t'f(x') = Z
(pro konkávní funkce to funguje přesně naopak)
Nerovnost tedy můžeme popsat floskulí: „funkční hodnota konvexní kombinace je menší než konvexní kombinace funkčních hodnot“. Když tuto duchaplnou větu o sečně pošeptáte na rande nějaké sličné slečně, zcela jistě zareaguje svlečně. I když je z obrázku patrné, že se jedná o vcelku triviální geometrický postřeh.
Abychom se mohli vrátit k té statistické entropii a ukázat si, že pro jakékoliv rozdělení do n hodnot musí být menší než ln(n), budeme potřebovat zobecnění Jensenovy nerovnosti pro n bodů, což znamená, že si tu duchaplnou formulku rozepíšeme pro konvexní kombinaci n čísel (x1, x2, ..., xn):
f(∑ ti * xi) <= ∑ ti * f(xi)
anebo bez sumačního znaménka
f(t1 * x1 + t2 * x2 + ... + tn * xn) <= t1 * f(x1) + t2 * f(x2) + ... + tn * f(xn) (tímto způsobem si můžeme například dokázat známou nerovnost mezi aritmetickým a geometrickým průměrem)
Teď si za koeficienty konvexní kombinace vezmeme:
ti = 1/n (pro každé i)
a když si tu nerovnost přepíšeme s těmito koeficienty, dostaneme:
f((x1 + x2 + ... + xn)/n) <= (f(x1) + f(x2) + ... + f(xn))/n
dále za xi dosadíme pravděpodobnosti pi (jejichž součet je 1):
f((p1 + p2 + ... + pn)/n) = f(1/n) <= (f(p1) + f(p2) + ... + f(pn))/n
a jelikož n>0, můžeme obě strany pronásobit:
n f(1/n) <= f(p1) + f(p2) + ... +f(pn)
Nakonec tuhle krásnou nerovnost aplikujeme na konvexní funkci f(x) = x*ln(x)
n * (1/n) * ln(1/n) <= p1 * ln(p1) + p2 * ln(p2) +...+ pn * ln(pn)
To napravo je záporná entropie -H a nalevo zůstane ln(1/n), takže:
- ln(n) <= -H
a po vynásobení nerovnosti -1 (a změně smyslu nerovnosti!) máme:
ln(n) >= H
QED
Článek je redakčně upravenou verzí blogového příspěvku na serveru
iDNES.cz. Publikováno s laskavým svolením autora.
Další díly a původní texty jsou dostupné na blogu Jana Řeháčka.