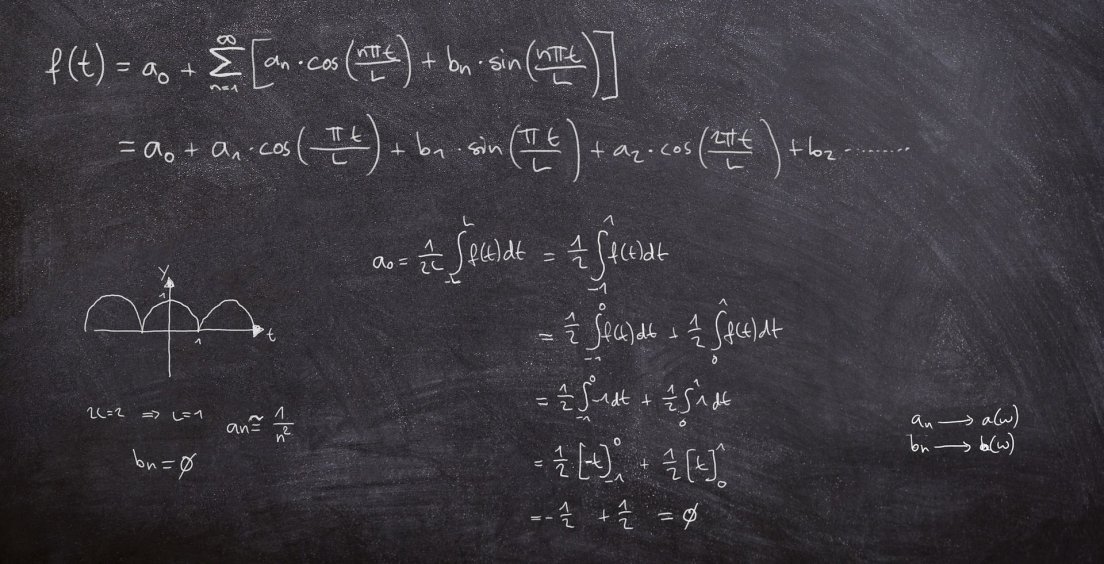V počítačové grafice (zejm. v robotice a videohrách) se s úspěchem používají tzv. homogenní souřadnice, které nám umožňují rozšířit akční radius maticových transformací. Jejich základy leží v poměrně ezoterické části geometrie.
V člověku se odpradávna přetahuje lpění na starém s touhou po novém. Na jedné straně tíhneme k bezpečí důvěrně známého prostředí, k souřadné soustavě z dávno prověřených hodnot. Jen neradi měníme své zaběhnuté zvyklosti a myšlenkové pochody. Instinktivně se bráníme náhlým změnám každodenních rituálů a raději se plácáme ve starých dobrých myšlenkových papučích, které nám padnou tak akorát. Na druhé straně cítíme, že změna je život a že staré koleje dříve nebo později zarostou plazivým plevelem. A tak se volky nevolky vydáváme na rozbouřený oceán nejistoty v naději, že na konci plavby nás čekají zelené břehy Nového světa, a ne ostrá skaliska Patagonie. A jako každý slušně vychovaný risk, i tento přináší svůj zisk. Po protrpění porodních bolestí a prodělání dětských nemocí nám nový úhel pohledu obvykle otevře dříve netušené obzory.
Když se kvantová fyzika začala dívat na částice jako na vlny, spousta lidí si ťukalo na čelo. Klasický fyzik uvelebený ve svém deterministickém křesílku si musel na začátku 20. století připadat jako štěně zmítané ve víru horské řeky. Ale tento pohled přinesl tolik nových podnětů, že dnes už se nad dualitou vln a částic nikdo pohoršeně nepozastaví.
V našich osobních životech to funguje podobně. Vzpomeňte si, jak jste se žasli, když jste s novým spolupracovníkem vyrazili do hospody. Jeden dva frťany a z nudného suchara z vedlejší kanceláře se najednou stal zábavný společník, amatérský filozof či vítaný parťák do mariáše. A jinak to není ani v matematice.
V minulých dílech jsme viděli, jak je inspirativní pohlížet na body v rovině jako na komplexní čísla, na matice jako na lineární zobrazení či na funkce jako na prvky vektorového prostoru. Každá taková proměna kontextu nám umožnila hlubší pochopení zkoumaného objektu.
Jako je tomu u většiny dovedností, i schopnost adaptovat se na nová paradigmata je nutno trénovat. Matematika je na změnu náhledu výborným posilovacím cvičištěm. Pro potvrzení svých teorií nemusíte budovat namáhavá experimentální zařízení, ani se probírat stohy naměřených dat. Stačí vzít papír a tužku a trochu si přenastavit kolečka ve své vlastní hlavě.
Proto se dnes podíváme na důvěrně známé eukleidovské prostory jinými očima. Jedna malá změna perspektivy, jedna malá změna úhlu pohledu a rázem se ocitneme v bizarním světě projektivní geometrie, ve kterém jsou body přímkami, přímky rovinami a roviny jsou de facto celým prostorem. Ale tak divně pokrouceným, že jen čekáte, odkud na vás vyběhnou hroši s červenými podkolenkami. Vstup jen na vlastní nebezpečí.
Projektivizace
Na rovinu můžeme nahlížet dvěma způsoby. Buď pro nás bude základním stavebním kamenem bod (a s ním spojený polohový vektor) a pak si rovinu můžeme představovat jako standardní 2D vektorový prostor s jeho obvyklou eukleidovskou geometrií (horní obrázek).
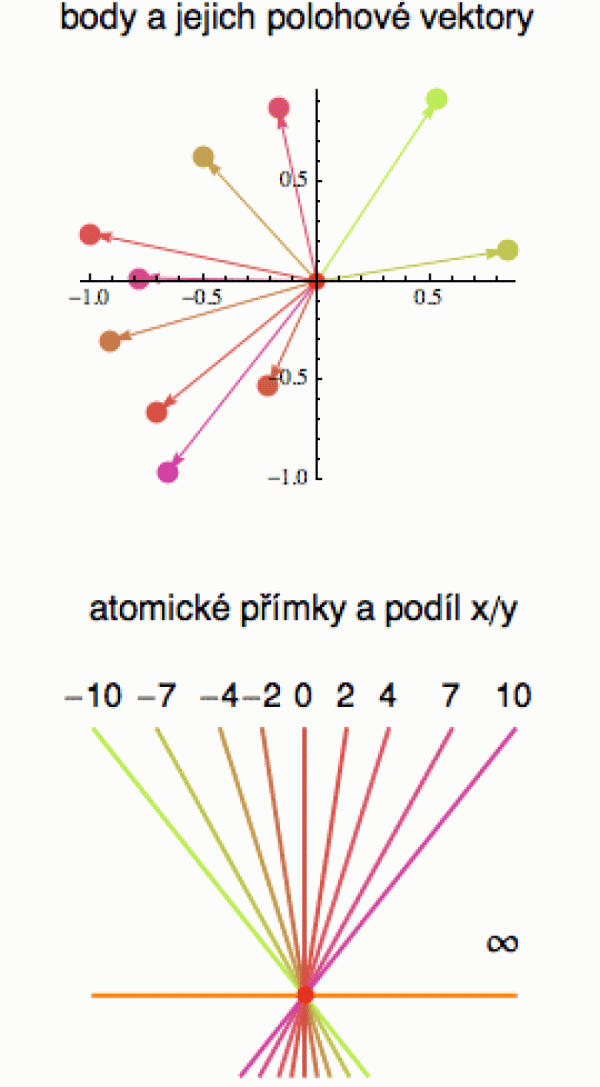
Anebo se můžeme postavit na pozici, kdy základním „atomem“ našeho prostoru bude přímka procházející počátkem a na tuto přímku (budu jí říkat „atomická“) pohlížet jako na dále nedělitelný objekt. Když si takovou přímkou zatočíte jako s vrtulí (dolní obrázek), zjistíte dvě zajímavé věci: jednak že s výjimkou počátku nemají takto vzniklé přímky žádné společné body, jednak že jejich sjednocení vyplní celou rovinu (to znamená, že každý nenulový bod leží právě na jedné atomické přímce). Tak jako se v eukleidovské geometrii prostor rozpadne na kolekci vzájemně rozdílných bodů, v projektivní se rozpadne na kolekci vzájemně rozdílných přímek. Každá taková přímka reprezentuje něco, čemu říkáme projektivní bod (protože na ty přímky můžeme nahlížet jako na paprsky centrální projekce) a kolekci všech možných „atomických“ přímek říkáme projektivní prostor (stejně jako u vektorových prostorů zde slovo „prostor“ označuje jen jakousi kolekci objektů – nemusí to tedy být nutně 3D útvar).
Z analytické geometrie v rovině vyplývá, že podíl souřadnic x/y je pro každou atomickou přímku konstantní (nezáleží na tom, pro který nenulový bod ho spočítáme), a můžeme ho tedy použít pro její charakterizaci (je to vlastně reciproká hodnota směrnice přímky). Na dolním obrázku jsou podíly naznačeny nad přímkami. Každému reálnému číslu r = x/y tedy odpovídá přesně jedna atomická přímka, a tedy přesně jeden projektivní bod. Pochopitelně s výjimkou osy x, kde bychom dělili 0. Této speciální přímce se přiřadí hodnota ∞ a říká se jí (projektivní) bod v nekonečnu. Když si nehorizontální přímky budete víc a víc naklánět, uvidíte, že jejich podíl r = x/y roste k nekonečnu, takže tato volba dává celkem dobrý smysl. Samozřejmě bychom si přímky mohli očíslovat přímo směrnicemi a pak by speciální roli převzala osa y. V projektivní geometrii je ale tato konvence – tedy x/y – běžnější.
V lineární algebře jsme se naučili, že dimenze prostoru je v podstatě počet čísel (souřadnic), které potřebujeme na to, abychom dokázali rozlišit jeho jednotlivé body. V projektivním prostoru na dolním obrázku nám postačí jedno číslo (podíl r = x/y). Proto se tento konkrétní projektivní prostor značí P1 nebo RP1, pokud chcete zdůraznit, že se jedná o reálný (a ne komplexní) projektivní prostor. A jak je u jednorozměrných objektů zvykem, říká se mu projektivní přímka. I když vypadá jako rovina.
To překládání názvosloví o dimenzi níž je trochu matoucí, takže to zopakuji: projektivní přímka je ta barevná kolekce (atomických) přímek. Každá z nich je projektivním bodem. Proto při četbě projektivní literatury musíte dávat pozor, zda se autor zmiňuje o „projektivních objektech“ (jejichž dimenze se našemu selskému rozumu jeví o jedničku vyšší), anebo jen o „objektech“. A přestože mluvíme o dimenzi, projektivní prostor není vektorovým prostorem v pravém slova smyslu, technicky je to varieta.
Na projektivní přímku se můžeme také dívat tak, že k běžné eukleidovské přímce přidáme bod v nekonečnu. Vezměme si třeba číselnou osu, která je asi nejběžnější eukleidovskou přímkou v této části galaxie. Jeden každý bod číselné osy – nějaké reálné číslo r – můžeme vzájemně jednoznačně přiřadit projektivnímu bodu (tj. atomické přímce), jejíž podíl souřadnic je x/y = r. Ta projektivní přímka má ale jeden bod navíc: „bod v nekonečnu“. Ten na eukleidovské přímce nenajdete, protože ∞ není reálné číslo.
Tato malá vada na kráse projektivních prostorů je ve skutečnosti jejich předností. Mají totiž – mimo jiné – za úkol „integrovat“ nekonečno do výpočetních struktur. Tedy přiblížit tuto nepřístupnou a odtažitou kvantitu obyčejnému člověku (mohli bychom to nazvat „nekonečno s lidskou tváří“).
Tím, že jsme přešli od dvojice čísel (x,y) k podílům x/y jsme z běžné 2D roviny udělali 1D projektivní přímku. Tomuto procesu se obecně říká projektivizace. Abychom si tento abstraktní přístup trochu ohmatali vlastníma rukama, podívejme se nejprve na dva příklady.
První příklad známe všichni ze školy. Jsou jím zlomky neboli racionální čísla. Na každý zlomek můžeme pohlížet jako na dvojici celých čísel: např. 2/5 odpovídají dvojici D = (2,5), a tedy i příslušnému bodu v jakési „diskrétní rovině“ (tedy rovině, kde uvažujeme pouze celá čísla – viz obrázek vpravo). Zlomky jsou tedy v jistém smyslu projektivizací dvojic celých čísel. Jen musíme mít na zřeteli, že jakékoliv násobky příslušné dvojice, třeba (4,10), (6,15), (8,20) atd., odpovídají stále stejnému zlomku, protože 2/5 = 4/10 = 6/15 = 8/20 = ...
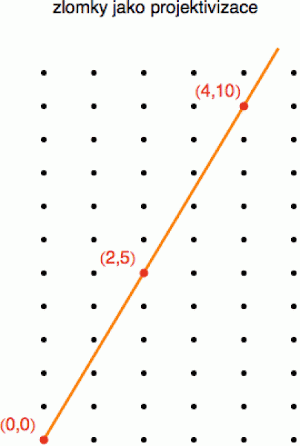
Jedním ze způsobů, jak tuto skutečnost nějak matematicky uchopit, je definovat na těchto dvojicích tzv. třídy ekvivalence. Dvě dvojice D1 a D2 prohlásíme za ekvivalentní (D1~D2), pokud je poměr jejich souřadnic stejný: např. (2,5) ~ (4,10). V tomto pojetí pak na zlomky nepohlížíme jako na dvojice celých čísel (to by vedlo k nejednoznačnosti), ale jako na třídy ekvivalence na těchto dvojicích definované. Zlomek 2/5 tedy není nic jiného než reprezentant třídy ekvivalence, která mj. obsahuje dvojice (2,5), (4,10) atd. Pro praktické počítání si pak z každé třídy vybereme reprezentanta s nesoudělným čitatelem a jmenovatelem (tj. zlomek, který se už nedá „zkrátit“).
Připomínám, že ekvivalence je speciální relace) (souvztažnost mezi dvěma objekty), která splňuje několik základních pravidel: je reflexivní (každý prvek je ekvivalentní sám sobě: x~x), je symetrická (můžeme prohodit pořadí: x~y právě tehdy, pokud y~x) a je tranzitivní (ekvivalence se „přenáší“: x~y a y~z implikuje x~z). Tj. je-li Tonda ekvivalentní Petrovi a Petr ekvivalentní Karlovi, pak je také Tonda ekvivalentní Karlovi. V čem? No třeba ve fotbale…
Pokud jste tohle malé opáčko ze základní školy vstřebali, máte vyhráno. Projektivní prostory jsou v podstatě zobecněním této konstrukce a můžete se na ně dívat jako na třídy ekvivalence na vektorových prostorech, kde dva vektory považujeme za ekvivalentní, pokud je jeden z nich skalárním násobkem druhého. Každá výše zmíněná atomická přímka je potom jednou takovou třídou ekvivalence.
Druhý příklad se týká zvláštního typu zobrazení. Lineární lomené funkce jsou podíly lineárních funkcí:
f(x) = (ax + b) / (cx + d), kde a, b, c, d jsou konstanty
Složením dvou takových funkcí vznikne opět lineární lomená funkce. Můžete si to sami ověřit:
Vezměme si f(x) = (8x + 3) / (5x + 2) a g(x) = (2x + 1) / (3x + 2) a složením dostanete:
f(g(x)) = (25x + 14) / (16x + 9) nebo v obráceném gardu g(f(x)) = (21x + 8) / (34x + 13)
Zatímco exponenciálu či kvadratickou parabolu naleznete všude možně, podíl lineárních funkcí je v aplikacích poměrně vzácným hostem. Možná vám na střední škole nebylo moc jasné, proč se kolem těchto monster vlastně dělá takový humbuk. Je to hlavně proto, že v komplexním oboru mají velmi zajímavé vlastnosti a jsou v jistém smyslu vstupní branou do neeukleidovských, přesněji řečeno hyperbolických, geometrií (ale o tom až za čas).
Matematici se velmi brzy dovtípili, že ty čtyři konstanty z definice by se daly poskládat do matice A = ((a,b),(c,d)) a začali se zajímat, zda mezi těmito funkcemi a maticemi neexistuje nějaký vztah. Mezi jejich vlastnostmi totiž existuje několik paralel (zkuste si třeba místo skládání zobrazení nahoře prostě vynásobit příslušné matice).
Připomeňme si, že na matice 2x2 se můžeme dívat jako na lineární zobrazení z R2 do R2. Naše funkce f a g ale fungují z R do R, a navíc nejsou samy o sobě lineární. Jsou však podílem lineárních funkcí. A to nás přivede k myšlence podívat se na matice projektivníma očima. Což si takhle vzít vektory, které ty matice zobrazují, a vydělením jejich souřadnic přejít k projektivnímu prostoru?
Zobrazení dané maticí A operuje na vektoru u = (x,y) takto:
A.u = A.(x,y) = (ax + by,cx + dy)
Když si teď označíme podíl vstupních souřadnic jako z = x/y, dostaneme pro podíl výstupních souřadnic:
(ax + by) / (cx + dy) = (az + b) / (cz + d) = f(z)
Vidíme tedy, že matice A dělá s vektory přesně ty samé psí kusy, odpovídající funkci f s podíly jejich souřadnic. Lineární lomená funkce f je projektivizací zobrazení daného maticí A.
Všechna taková zobrazení f se tedy dají reprezentovat vhodnou maticí A. To vypadá na první pohled jen jako takové plané abstraktní plácání, ale jen do okamžiku, než si uvědomíme, že jedním z takových zobrazení f je i translace f(x) = x + t (kde reálné číslo t je magnituda posunutí). Pro názornost ji ještě přepíšu, aby vypadala jako lineární lomená funkce: f(x) = (x + t) / (0x + 1). Matice odpovídající translaci v projektivním prostoru je tedy A = ((1,t),(0,1)). A tento jednoduchý poznatek se stal základem výše zmíněných aplikací v počítačové grafice (jak uvidíme v poslední sekci).
Závěrem tohoto oddílu bych jen poznamenal, že vlastní vektory příslušné matice A přesně odpovídají pevným bodům zobrazení f (tedy hodnotám x splňujícím f(x) = x), jak si můžete sami ověřit. Ta provázanost matic 2x2 a lineárních lomených funkcí je tedy hlubší, než by se mohlo zdát, a v praxi si můžete vybrat, zda počítat přímo ty pevné body, anebo raději vlastní čísla odpovídajících matic.
V 2D rovině si tedy prostřednictvím projektivizace můžeme vytvořit vcelku funkční model 1D prostoru (projektivní přímka), který nám - mimo jiné - umožní studovat vlastnosti některých 1D funkcí pomocí metod lineární algebry. Jako vedlejší produkt dostaneme i snadnější manipulaci s nekonečnem, které se v tomto modelu dá reprezentovat buď osou x nebo osou y (podle toho zda preferujete podíl x/y nebo y/x). Jeho zobrazování hraje při studiu lineárních lomených funkcí důležitou roli.
Z pohledu lineární algebry je projektivní prostor prostorem „směrů“. A není to myšlenka nijak nepřirozená. Třeba vlastní vektory jsou spíše „vlastní směry“, protože se dají libovolně přeškálovat (ať si vezmete jakýkoliv nenulový násobek vlastního vektoru, bude stále splňovat příslušný definiční vztah).
Dívat se na atomické přímky jako na „směry“ je geometricky intuitivní. Algebraicky docílíme téhož efektu, když přejdeme ke třídám ekvivalence. Všechny vektory, které se na sebe dají převést skalárním vynásobením, považujeme za „nerozlišitelné“ (stejně jako ekvivalentní zlomky). Konkrétněji: u~v, pokud existuje skalár s ≠ 0, tak že u = sv. Např. (1,2,4) ~ (2,4,8). Takto vyzbrojeni se můžeme přenést do vyšších dimenzí.
Ani algebraický, ani geometrický přístup totiž není nijak vázaný na konkrétní vlastnosti roviny R2 (a jejího projektivního souputníka P1), ale dá se provést na obecném vektorovém prostoru V. Prvky příslušného projektivního prostoru pak budou v geometrickém náhledu přímky procházející počátkem nebo výše popsané třídy ekvivalence vektorů v náhledu algebraickém. Nic nového pod sluncem, jen nám trochu přibude souřadnic.
Obecně platí, že n-dimenzionální projektivní prostor se zkonstruuje z výchozího (n + 1)-dimenzionálního vektorového prostoru, takže to dimenzionální žonglování mezi projektivními a neprojektivními objekty nás bude provázet i nadále. Abychom do toho ale nespadli moc natvrdo, podíváme se nejprve na (reálnou) projektivní rovinu P2 (kterou si vytesáme z běžného 3D prostoru). A už tady uvidíme, že geometrie směrů je trochu jiná než geometrie bodů.
Projektivní rovina
Projektivní rovinu si vytvoříme podobně jako projektivní přímku. Pohodlně se usadíme ve vektorovém prostoru R3 a za „body“ projektivní roviny prohlásíme královským dekretem všechny přímky procházející počátkem O. Stejně jako v předchozí sekci se na každou atomickou přímku budeme dívat jako na nedělitelný atom naší mystické projektivní roviny. V tomto případě už ale nemáme k dispozici její směrnici (respektive reciprokou hodnotu), a tak se nebudeme spoléhat na algebru, ale připravíme si místo toho takovou geometrickou vychytávku (k algebře se vrátím v poslední sekci).
V tom „výchozím“ 3D prostoru si kromě souřadné roviny x-y s rovnicí z = 0 (té budu říkat P) ještě označíme posunutou rovinu odpovídající rovnici z = 1 (a té budu říkat Q). To posunutí může být o libovolný kousek, ale vzhledem k tomu, že vše můžeme přeškálovat, je jednička rozumná volba měřítka.
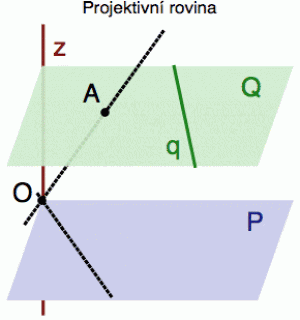
Lehce si teď rozmyslíme, že všechny atomické přímky vedoucí počátkem O (tedy naše projektivní body) se dělí do dvou skupin. Buď taková přímka leží celá v rovině P a nebo protíná rovinu Q právě v jednom bodě. To není potřeba počítat - to je vidět z obrázku. Těm atomickým přímkám, které zůstaly v rovině P se říká „body v nekonečnu“ (protože nemají žádný „konečný“ průnik s rovinou Q) a kolekci všech těchto přímek (tedy projektivních bodů v nekonečnu) se říká „přímka v nekonečnu“. Rovina P je tedy v našem modelu (projektivní) přímkou v nekonečnu. Na rozdíl od předchozí sekce, kde byl bod v nekonečnu jen jeden (osa x), máme tady celou projektivní přímku takových bodů.
A teď ta vychytávka. Projektivní body (naše atomické přímky) tedy buď odpovídají „tradičním“ bodům v eukleidovské rovině Q (na obrázku např. atomická přímka OA, kde bod A je jakýmsi reprezentantem příslušného projektivního bodu v rovině Q, a hraje tedy roli směrnice z předchozí sekce), anebo „ideálním“ bodům v nekonečnu (to je ta druhá vytečkovaná přímka). Proto se na projektivní rovinu můžeme dívat jako na tradiční rovinu (v našem případě Q), ke které jsme přidali hafo bodů v nekonečnu. Jeden pro každou atomickou přímku v rovině P. A protože každá atomická přímka v rovině P představuje určitý směr, který se dá přenést do roviny Q, laicky si to můžete představit tak, že k tradiční rovině jsme přidali body „na horizontu“ (kterých je přesně tolik, kolik je směrů v rovině P).
V jistém smyslu se projektivní rovina snaží formalizovat známý „lidový poznatek“, že dvě rovnoběžky se protínají v nekonečnu. Podívejme se na tuto konstrukci podrobněji (nezájemci o toto téma mohou zbytek podsekce přeskočit).
Projektivní přímkou bude jakákoliv rovina R procházející počátkem. Tato rovina se pochopitelně skládá z mnoha atomických přímek procházejících počátkem neboli v projektivní řeči: tato projektivní přímka se skládá z mnoha projektivních bodů. Pokud rovina R náhodou splyne s rovinou P, máme co do činění s projektivní přímkou v nekonečnu. Ve všech ostatních případech je projektivní přímka (tedy rovina R) jednoznačně určena běžnou přímkou q v rovině Q (stačí si vzít dva různé body přímky q, řekněme M a N, a uvažovat rovinu danou vektory OM a ON). A naopak, každá projektivní přímka (tedy rovina R ≠ P) protne rovinu Q v jednoznačně určené přímce q. Projektivní přímky tedy odpovídají buď běžným přímkám v rovině Q (pokud je R ≠ P), anebo projektivní přímce v nekonečnu (pokud je R = P).
Zhluboka nadechnout. Zhluboka vydechnout.
Dvě různé roviny R a R' (procházející počátkem O) se protínají v přímce r, která musí nutně procházet počátkem neboli v projektivní řeči: dvě projektivní přímky se protínají v projektivním bodu. Pokud tato přímka r protíná rovinu Q, řekněme v bodu X, máme obvyklou situaci, tedy dvě projektivní přímky (dané rovinami R a R') se protínají v konečném projektivním bodu, odpovídajícím přímce r = OX. V tomto případě roviny R a R' odpovídají dvěma různoběžkám q a q' v rovině Q, protínajících se v bodu X (q je průnikem R a Q, zatímco q' je průnikem R' a Q).
Zajímavější případ nastane, pokud roviny R a R' budou odpovídat rovnoběžkám q a q' v rovině Q. Průnikem těchto rovin pak bude přímka p ležící kompletně v rovině P. To není úplně triviální. Předpokládejme, že obě rovnoběžky v Q jsou určeny stejným vektorem u. Protože P a Q jsou rovnoběžné, tento vektor u je také součástí roviny P. Normálové vektory n a n' těchto rovin musí být na vektor u kolmé (protože u leží v obou). Tedy u⟂n a také u⟂n'. Průsečík obou rovin ale musí být kolmý na oba normálové vektory n a n' a musí to tedy být vektor u (či jeho násobek). Ten pak v rovině P určí přímku p, která je průsečíkem rovin R a R'. Řečeno projektivně: dvě projektivní přímky odpovídající rovnoběžkám q a q' (a tedy rovinám R a R') se protínají v projektivním bodu v nekonečnu, a to v přímce p (ta je pak mimochodem rovnoběžná k oběma přímkám q a q' v běžném smyslu – všechny tři jsou směrově určeny vektorem u).
Ta přímka p (respektive její směr) zde tedy zastupuje to, čemu bychom říkali bod na horizontu. A to je zhruba laická představa o tom, kde se dvě rovnoběžky q a q' vlastně protínají (hezké „vyprávěcí“ vysvětlení tohoto fenoménu najdete zde).
Projektivní geometrie nám opět umožňuje „manipulovat“ s nekonečnem a v tomto případě precizně specifikovat objekt, který odpovídá průsečíku dvou rovnoběžek v tradiční eukleidovské rovině Q. A nemusíme používat vágní básnické obraty, že tyto dvě přímky se protínají „v dáli na šedavém horizontu“. Ale je to makačka na bednu.
To, že musíte v hlavě neustále přepínat mezi projektivními přímkami (roviny procházející počátkem), atomickými přímkami (projektivní body) a občas ještě běžnými přímkami (jako ty v rovině Q), je matoucí a nepohodlné. Proto si spousta lidí projektivní rovinu představuje jinak.
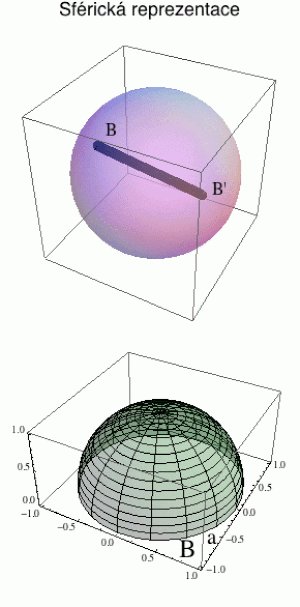
Každá z atomických přímek protíná jednotkovou sféru. Můžeme si tedy projektivní body představovat jako body na sféře, což je poměrně snadno stravitelná reprezentace (sláva, projektivní body jsou skutečně body!). Má to ale malý háček. Ty průsečíky jsou dva, takže každý bude mít svého dvojníka na protilehlé straně (na horním obrázku jsou to body B a B'). A ty pochopitelně považujeme za jeden atomický objekt (jako byste současně existovali v Česku a na Novém Zélandu – viz úvod tohoto videa).
Jedním ze způsobů, jak se vyvléci z toho ztotožnění, je vybrat si z každé dvojice průsečíků jeden bod, např. ten na severní polokouli s tím, že na rovníku si vybereme ty, jejichž východní délka bude z polootevřeného intervalu [0°,180°) – ano, i z té dvojice 0°, 180° si musíme vybrat pouze jeden.
Tahle představa funguje celkem dobře, ale když se po takto získané projektivní rovině začnete procházet, zjistíte zajímavou věc. Ona se nedá orientovat, tedy nedá se přesně určit, co je vnější strana a co vnitřní (podobně jako u Möbiova pásku).
Představme si, že pochodujeme podél poledníkové kružnice (viz spodní obrázek) a to tak, že vystartujeme z bodu B a dojdeme do protilehlého (antipodálního) bodu B', který sice není vidět, ale je de facto tím samým projektivním bodem (nezapomeňte na ztotožnění). Jenže v okamžiku, kdy do toho bodu B dorazíte (a jste tedy zase tam, odkud jste vystartovali), tak zjistíte, že to, co jste měli po pravé straně (například bod a na spodním obrázku), je najednou nalevo a naopak. Díky té ekvivalenci protilehlých bodů se strany prohodily (dvojník bodu a je na druhé straně). Což je mimochodem přesně to samé, co by nás potkalo při procházce podél Möbiova pásku: vystartovali bychom podél pomyslné středové dělicí čáry a jednu z hran Möbiova pásku bychom označili jako nalevo, jenže ouha, po průchodu páskem bychom zjistili, že ta hrana, která je nalevo, je najednou napravo.
Tím netvrdím, že projektivní rovina je to samé, co Möbiův pásek, ale výše popsané chování naznačuje, že orientovatelná asi nebude. Pokud si v bodě B definujete normálu jako vektorový součin směru, ve kterém pochodujete, a směru, ve kterém vidíte bod a, pak ten první zůstane v bodě B' zachován (pokračujete stále podél poledníku), ale ten druhý se prohodí. A tím pádem se prohodí i normála (techničtější popis je zde).
Neorientovatelnost je globální vlastnost. Z lokálních pozorování ji nezjistíte, stejně jako u Möbiova pásku. Pokud se budete poflakovat jen po malém okolí projektivní roviny, tak nic podezřelého nezaregistrujete. Jakmile ale vyrazíte na cestu kolem světa, zjistíte, že to přidávání bodů v nekonečnu vám ho pěkně pokroutilo.
Mimochodem, projektivní rovina se, podobně jako Möbiův pásek nebo Kleinova lahev, dá vytvořit z jednotkového čtverce vhodnou identifikací – či slepením – stran (zde je velmi hezký souhrn, kde jsou ta různá slepení naznačena šipčičkami; a zde je podrobnější rozbor pro projektivní rovinu).
Milovníci sci-fi si pak mohou pohrát s myšlenkou, jak by asi náš vesmír vypadal, kdybychom místo v eukleidovském prostoru žili v projektivním. To by se nám taky mohlo stát, že vyrazíme na okružní plavbu a poté, co se vrátíme, budeme mít srdce napravo (stejně jako krab ze známé möbiovské animace, který má po průchodu páskem klepeto na opačné straně). A vaše pravá rukavice v kapse bude najednou levá…
Ale tohle je spíš hračka pro matematiky. Pro počítačové grafiky je vhodnější předchozí pohled, ze kterého je lépe patrná souvislost projektivního prostoru s eukleidovským prostorem. Takový pohled jsme pochopitelně mohli adoptovat i v předchozí sekci a místo reciprokých směrnic jsme mohli souvztažnost s běžnou eukleidovskou přímkou odvodit narýsováním přímky y = 1(která by hrála roli roviny Q). Mezi projektivními body a body této přímky opět existuje vzájemně jednoznačné spárování s tím, že ta projektivní přímka obsahuje jeden bod navíc – bod v nekonečnu (osu x).
Homogenní souřadnice
Minule jsme viděli, že většina přirozených geometrických transformací (rotace, zrcadlení, změna měřítka neboli přeškálování) lze popsat pomocí násobení vhodných matic. Jedna důležitá transformace se tak ale popsat nedá – translace neboli posunutí.
A je lehce vidět proč. Každá maticová transformace F(u)=A.u zobrazuje nulový vektor 0 zpátky do počátku, tedy splňuje F(0)=A.0 = 0. A to translace o nenulový vektor a nesplňuje ani náhodou. Z její formulky T(u) = u + a lehce dostaneme T(0) = a, takže milá translace zobrazuje nulový vektor do vektoru nenulového. Nelze ji tedy popsat maticí.
To je pro tvůrce videoher a dalších vizuálních pomůcek problém. Translace je esenciální. Pokud vás po obrazovce honí nějaké příšerky, tak tu translaci potřebujete dosti urgentně, protože bez ní se doslova nepohnete z místa a hladoví baziliškové vás sežerou.
Na první pohled by se mohlo zdát, že to není zase takový průšvih. No tak holt ta maticová zobrazení u --> A.u budeme příležitostně skládat s translační formulkou u --> u + a. To je ale pro větší počet transformací (a ve videohrách je jich neúrekom) nepraktické.
Ve druhém příkladu úvodní sekce jsme viděli, že translace v projektivním prostoru P1 se dá vyjádřit pomocí matic typu 2x2, fungujících v eukleidovském prostoru R2, ze kterého jsme při konstrukci P1 vyšli. Tak prostě přidáme jednu souřadnici a bude vystaráno. Vyjdeme z prostoru R4, z něho uděláme projektivizací P3 (omezíme se na přímky procházející počátkem), a přitom o nic podstatného z 3D geometrie nepřijdeme, protože ten prostor P3 bude stále obsahovat vznášející se kopii R3 v poloze w = 1 (podobně jako v předchozí sekci ta zelená rovina Q představovala kopii prostoru R2, vznášející se v poloze z = 1 uprostřed P2).
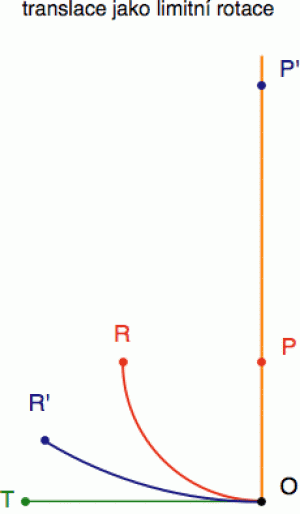
Mimochodem, už několikrát jsme dnes viděli, že projektivní prostor je geometrickým pokusem o zkrocení zlého nekonečna. I vyjádření translací pomocí matic je toho v jistém smyslu dokladem, protože na translaci se můžeme dívat jako na limitní případ rotace (se středem v nekonečnu). Podívejte se na obrázek vpravo. Rotace se středem v bodu P otočí bod O do bodu R. Rotace ze středu P' (o příslušně zmenšený úhel) otočí bod O do bodu R'. Protože poloměr rotace ze středu P' je větší, modrá dráha rotovaného bodu O je podstatně přímější. A čím více střed P' posunujeme nahoru do nekonečna, tím „rovnější“ bude výsledná dráha. V limitním případě, kdy se střed P' odstěhuje do nekonečna (a úhel už bude pouze infinitesimální), bude ta dráha zcela rovná – rotace se „proměnila“ v translaci.
Ale zpátky na zem. Uniformní vyjádření všech transformací pomocí matic nám umožní podstatně zeštíhlit jejich algoritmické zpracování. Můžeme si například předpočítat součiny velkých skupin matic a aplikovat je pak na body prostoru najednou (takovému procesu se říká batch multiplication). Budeme se ale muset naučit v projektivním prostoru používat souřadnice.
Podívejme se nejprve, jak popsat souřadnice projektivních bodů (atomických přímek). Nejjednodušší variantou je vypůjčit si souřadnice z „výchozího“ eukleidovského prostoru, jehož projektivizací jsme projektivní prostor vytvořili. Tedy pro body z P1 si vypůjčíme souřadnice z R2: p=(x,y), pro body z P2 si je vypůjčíme z R3: p=(x,y,z) a obdobně ve vyšších dimenzích.
Musíme ale mít na paměti, že atomické přímky jsou de facto třídy ekvivalence, a že tedy projektivní body mohou mít více ekvivalentních souřadných zápisů (podobně jako zlomky v úvodu). Např. p = (2,3) = (3.0,4.5) atd. Těmto vypůjčeným souřadnicím říkáme homogenní a abychom zdůraznili, že u projektivních objektů nás nezajímají ani tak nominální hodnoty jako jejich podíly, tak ty homogenní souřadnice značíme dvojtečkou, tedy p = (2:3).
U vědomí toho, že homogenní souřadnice můžeme pronásobit libovolným číslem, se často používá normalizace spočívající v tom, že poslední souřadnici nastavíme na 1. Např. p = (2:3) je to samé co p = (2/3:1). To se nedá provést, pouze pokud je poslední souřadnice 0. Proto většina homogenních souřadnic, se kterými se v životě setkáte (např. na autobusové zastávce linky Praha-Mělník-Nekonečno) má poslední souřadnici buď 1 (eukleidovské body) nebo 0 (body v nekonečnu). Např. bod q∈P3 s homogenními souřadnicemi q = (2:3:4:5) můžeme zapsat v normalizovaném tvaru jako q = (0.4,0.6,0.8,1.0) a bude tedy odpovídat 3D eukleidovskému bodu (0.4,0.6,0.8). Naopak bod q = (2:3:3:0) odpovídá bodu v nekonečnu a na ten raději sahat nebudeme – násobit nulu si troufne pouze Sysifos.
(opravdu otrlé povahy mohou provést normalizaci tak, že pozvou sovětské tanky a ty tu projektivní rovinu rozjezdí na cimpr campr)
Sečteno a podtrženo: Projektivní prostor P3 jsme vytvořili projektivizací prostoru R4 a následným omezením se na podprostor w = 1 jsme v něm nalezli kopii eukleidovského prostoru R3, ve kterém můžeme stále provádět 3D psí kusy. Podprostor w = 0 bude analogicky s předchozí sekcí reprezentovat „body v nekonečnu“. A tady už jich je opravdu celý pytel. Schválně, jestli najdete dvě rovnoběžky v prostoru w = 1 (analogie roviny Q), které se protínají v „ideálním bodu“ (1:2:3:0).
Abychom toto vyjádření nekonečna ocenili, vraťme se na chvíli do úvodního prostoru P1. Pokud bychom v něm atomické přímky popsali jejich reciprokými směrnicemi x/y, tak se nám na hraniční přímce (osa x) bude nekonečno neustále plést pod nohy. S homogenními souřadnicemi ho ale lehce obeplujeme, protože osa x má homogenní vyjádření (1:0) - což mimochodem vyjadřuje to, co většina koumesů už dávno intuitivně tuší: 1:0=1/0=∞ (důvod, proč mají žáci ve škole zapovězeno dělit nulou je stejný, jako proč mají zapovězeno hrát si se sirkami - při nesprávné manipulaci může obojí vést ke katastrofálním důsledkům).
Na procvičení se ještě zastavme v projektivní rovině P2. Projektivní přímka je rovina procházející počátkem a má tedy rovnici ax + by + cz = 0 (pro nějaké vhodně zvolené reálné konstanty a,b,c). Vidíte, že projektivní rovnice v P2 je o něco symetričtější než „obyčejná“ rovnice přímky v R2: ax + by + c = 0. Navíc je projektivní přímka popsána třemi parametry (a,b,c), stejně jako je projektivní bod popsán třemi homogenními souřadnicemi (a:b:c). To vede v projektivní geometrii ke známé dualitě) bodů a přímek. Přímky a body jsou objekty téhož ražení a jejich rozlišení je pouze věcí interpretace.
Projektivní prostory (a jejich homogenní souřadnice) nám také umožňují odstranit z geometrie různé speciální případy, které z nekonečen vyplývají.
Bezoutova věta, zabývající se počtem průsečíků polynomiálních křivek (tedy souběžným řešení polynomiálních rovnic) zhruba tvrdí, že křivky popsané polynomem n-tého stupně a polynomem m-tého stupně budou mít nxm průsečíků (řešení).
A skutečně: dvě přímky, popsané polynomem 1. stupně, mají pouze 1x1 = 1 průsečík (tedy až na rovnoběžky, ale ty už jsme projektivně vyřídili). Parabola je popsaná polynomem 2. stupně (kvadratickým), a má tudíž s přímkou 2x1 = 2 průsečíky. Tedy opět až na výjimky. Třeba ta nejjednodušší parabola y = x2 má s přímkou y = 0 (osa x) pouze jeden průsečík. Kde je ten druhý?
Ten druhý si chrápe v nekonečnu a můžeme ho probudit pomocí homogenních souřadnic. Připomeňme si, že normalizované homogenní souřadnice (x/z,y/z,1) nám „prozrazují“ eukleidovské souřadnice. Parabola y = x2 proto bude mít v homogenních souřadnicích rovnici: (y/z) = (x/z) 2 a po úpravě yz = x2. Současně ale řešíme rovnici x = 0 (ta i po záměně x --> x/z vyjde nastejno, protože zlomek je nula, pokud je jeho čitatel nula).
Rovnice x = 0 a yz = x2 implikují x = 0 = yz. Tato forma naznačuje dvě řešení. To první je v normalizovaném tvaru (0,0,1) a odpovídá průsečíku s eukleidovskými souřadnicemi (0,0). O něm jsme už věděli. To druhé je (0,1,0) a odpovídá ose y, která patří mezi přímky roviny P (z předchozí sekce) a reprezentuje tedy projektivní bod v nekonečnu (více o kuželosečkách v projektivním prostoru zde). Pokud máte vrozený cit pro symetrii, budete se v projektivním prostoru cítit jako doma.
Ale zpátky k transformacím. Abychom se mohli maticově popasovat s translací ve vektorovém prostoru R3, provedeme tedy celou operaci v projektivním prostoru P3 a to znamená, že ke třem standardním souřadnicím x,y,z prostoru R3 musíme přidat ještě čtvrtou (obvykle značenou w), abychom mohli používat homogenní souřadnice (x:y:z:w).
Matice, zobrazující takto rozšířené vektory, jsou pak pochopitelně typu 4x4. Poslední element vpravo dole je obvykle 1, protože matice se – stejně jako homogenní souřadnice – dají přeškálovat (pouze ve speciálních případech, kdy potřebujete pracovat s bodem v nekonečnu, v tom rohu najdete 0). Translační vektor pak leží v posledním sloupci (nad tou rohovou jedničkou), stejně jako v 1D příkladu z úvodu (kde parametr t figuroval nad tou poslední jedničkou). Můžete si provést maticové vynásobení a přesvědčit se, že tyto elementy opravdu kontrolují translaci. Matice 3x3 nalevo od translačního vektoru pak odpovídá běžným lineárním zobrazením (však ty první tři pozice také odpovídají běžným eukleidovským souřadnicím).
Tímto trikem se nám podařilo reprezentovat o něco širší třídu geometrických transformací, kterým se říká afinní a můžete si je představovat jako běžné lineární transformace plus posunutí (translace).
Zbývá otázka, k čemu jsou tři čísla dole v posledním řádku matice (nalevo od té rohové jedničky). Díky nim se akční rádius maticových zobrazení dále rozšíří o tzv. projektivní transformace (též zvané homografie), v praxi používané například pro podchycení perspektivy (pár příkladů najdete zde).
Pro afinní zobrazení, ale tu poslední řádku nepotřebujeme, takže v aplikacích se často vypouští a z důvodu rychlejšího výpočtu se používají pouze matice typu 3x4.
Kdo by se v tom chtěl vrtat podrobněji, může mrknout sem nebo sem.
Článek je redakčně upravenou verzí blogového příspěvku na serveru iDNES.cz. Publikováno s laskavým svolením autora. Další díly a původní texty jsou dostupné na blogu Jana Řeháčka.