Na vojně nám velitel útvaru trpělivě vtloukal do hlavy, že při boji se situace mění každým okamžikem. A to platí i mimo rámec vojenské přípravy. Proto se matematika musela naučit popisovat stav světa, který je v neustálém pohybu.
To, že se věci neustále vyvíjejí, tušili už staří Řekové (panta rhei). Jak ale lidstvo začalo objekty zmítané tokem událostí pozorovat, zjistilo, že občas se poměry uklidní a pozorovaný systém se výsledně dostane do ustáleného režimu (obvykle do nějaké formy ekvilibria), ve kterém se působící síly usmíří v rovnováze.
Kulička vhozená do hlubokého talíře se nakonec zastaví v nejhlubším bodě, planety obíhají po vcelku neměnných drahách, teplota v různých částech místnosti se dříve nebo později vyrovná. Než se ovšem ta kulička na dně talíře ustálí, musí si projít několika oblouky, které závisí na tom, odkud a jakou rychlostí jsme kuličku vypustili. Matematika proto rozlišuje tzv. transientní chování (rejdění kuličky po talíři), které závisí na počátečních podmínkách a v průběhu experimentu obvykle odezní, a asymptotické chování (trůnění kuličky uprostřed talíře), které charakterizuje ustálený stav a de facto nám ukazuje, jak se systém chová v limitě pro dostatečně velké hodnoty času.
Studiem takových procesů, od jednoduchého kyvadla až po komplexní vrtochy světové ekonomiky nebo počasí, se zabývá matematická disciplína zvaná dynamické systémy.
Dynamické systémy
Z pohledu matematiky tvoří dynamický systém dvojice (X, F), kde X je prostor stavů, ve kterém se dynamika odehrává, a F je funkce, popisující změnu stavu systému po uplynutí určitého času. Tím prostorem může být běžný n-rozměrný eukleidovský prostor, ale některé dynamické procesy se mohou rozvíjet i v abstraktnějším kontextu (např. v prostoru matic, posloupností nebo funkcí).
Když to řeknu obecnou češtinou - abychom definovali dynamický systém, musíme definovat jeho hřiště X a pravidla hry F. A prakticky všechno, co se vyvíjí v čase, se dá pozorovat optikou dynamických systémů.
Stav systému v čase t (např. momentální polohu kuličky v hlubokém talíři) budu značit symbolem x(t) a každý takový stav bude elementem z naší množiny X. Úkolem funkce F je potom popsat, jak se systém dostane ze stavu x(0) v čase 0 do stavu x(t) v čase t.
F: x(0) --> x(t)
Jak to ta funkce dělá, závisí zejména na tom, zda uvažujeme plynulý (spojitý) tok času, a nebo zda se spokojíme se znalostí stavu systému v nějakých předem určených časových intervalech (na čas se pak díváme jako na diskrétní veličinu).
Toto rozlišení indukuje rozdělení dynamických systémů na dvě základní kategorie - na spojité dynamické systémy, kdy nás zajímá stav systému x(t) pro libovolné reálné číslo t, a na diskrétní dynamické systémy, kdy máme informaci o systému pouze v celočíselných hodnotách času x(n).
Spojité systémy se tedy vyvíjejí podél křivek, zatímco ty diskrétní se z jednoho stavu do druhého přesunují doslova „skokem“ (můžete si to představovat tak, že na daný bod aplikujete určitou transformaci). Schematicky si to můžeme znázornit takto:
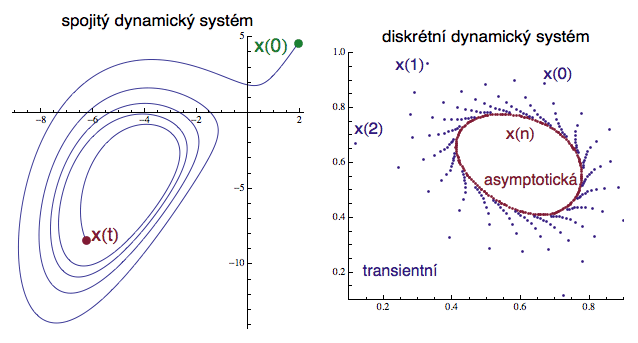
Při své cestě z počátečního stavu x(0) do pozdějšího stavu x(t) se
systém pohybuje po určité dráze, které říkáme orbita
nebo trajektorie. Její přesný tvar je zakódován ve funkci
F. U spojitých systémů se funkce F obvykle spočítá řešením
diferenciálních rovnic, a protože to není nic jednoduchého, ve zbytku
článku se budu zabývat pouze systémy diskrétními, kde je funkce F určena
iterováním (tedy opakovanou aplikací) nějaké definiční funkce f,
která na našem prostoru X funguje a která nám říká, jakým způsobem se
daný stav systému změní v následujícím okamžiku. To znamená, že ze
stavu x(0) = x v čase 0 se systém přesune nejprve do stavu
x(1) = f(x) v čase 1, pak do stavu x(2) =
f(f(x)) v čase 2 atd.
V pravé (diskrétní) části obrázku si všimněte rozdílu mezi transientní a asymptotickou fází.
Po startu z bodu x(0) začneme aplikovat funkci f a pečlivě vynášet polohu nově vzniklých bodů: x(n + 1) = f(x(n)), kde n je přirozené číslo.
Když budete jejich pohyb sledovat, zjistíte, že zprvu poskakují jako indiáni kolem ohně a pomalu se k němu přibližují. Ovšem až k ohni se nedostanou. Asymptotickým stavem (tedy stavem, ke kterému se dopracujeme pro vysoké hodnoty n) je zde malá uzavřená křivka (fialová), ke které sledovaná posloupnost bodů pomalu konverguje. Pokud byste vystartovali z jiného počátečního bodu, transientní chování (v modrém) bude jiné - budete kolem ohně poskakovat „v jiných stopách“, ale nakonec se k té asymptotické křivce prokoušete a budete křepčit podél ní. A samozřejmě, pokud byste si vzali počáteční stav x(0) přímo na fialové křivce, tak byste žádné transientní chování nepozorovali a jeli byste hned od začátku v asymptotickém režimu. A abychom byli konkrétní, tak vám funkci, která generovala diskrétní část předchozího obrázku, představím. V 80. letech ji zpopularizoval Kunihiko Kaneko, a přestože popisuje poměrně jednoduchý trojrozměrný systém, vykazuje překvapivě zajímavé dynamické vlastnosti. Přechod ze stavu (x, y, z) do stavu (X, Y, Z) probíhá podle pravidla:
X = a * x + (1 - a) * (1 – c * y2)
Y = z
Z = x
tedy schematicky: (X, Y, Z) = f(x, y, z), kde f je Kanekova funkce (Kaneko map).
Všimněte si, že ve funkci jsou kromě proměnných x, y, z (které určují pozorovaný stav), také dva parametry a, c, které modelují fyzikální (či jiné) vlastnosti celého systému. Při studiu dynamického chování se hodnoty parametrů zafixují a spočítají se trajektorie pro různé počáteční hodnoty (x, y, z), ze kterých se posléze odvodí dynamika systému. Nadstavbovým problémem pak je, jak se dynamika systému mění v závislosti na jeho parametrech.
Abychom si mohli pár orbit spočítat, nastavíme si parametry takto:
A = 0.33 a c = 1.06
a budeme zkoumat, jak se budou vyvíjet různé počáteční stavy - každou trojici čísel dosadíme do pravé strany, vyčíslíme a získanou trojici nových souřadnic opět dosadíme do pravé strany (mimochodem, dynamika Kanekovy funkce představuje dobré a celkem atraktivní cvičení pro začínající programátory). Tady jsou dva příklady pro dva počáteční stavy: (0, 0, 0) a (1, 2, 3):
(ukazuji vám tedy začátek každé orbity)
(0, 0, 0) --> (0.67, 0, 0) --> (0.8911, 0, 0.67) --> (0.964, 0.67, 0.8911) ...
(1, 2, 3) --> (-1.84, 3, 1) --> (-6.33, 1, -1.84) --> (-2.129, -1.84, -6.33) ...
(každá aplikace definiční funkce posune čas o jedničku)
Samotné počítání nám toho o dynamice systému ale mnoho neřekne. Obvykle si tu posloupnost bodů musíme vykreslit a podívat se, kam má namířeno (při vykreslování samozřejmě orbitu promítneme do nějaké dvourozměrné roviny). Chování dynamických systémů je poměrně komplikovaná záležitost s bohatou fenomenologií, ale asymptotické (výsledné) stavy se v zásadě dají rozdělit do tří základních kategorií.
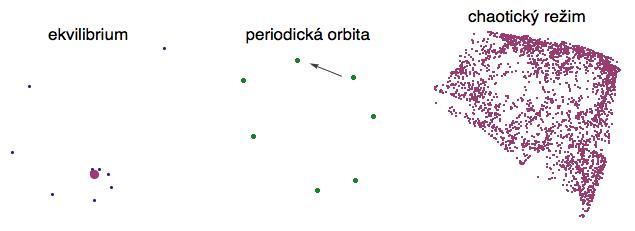
V levé části nás transientní chování (naznačené modrými body)
dovede k (fialovému) rovnovážnému stavu, ve kterém se chování
systému už dále nemění. Tento je samozřejmě charakterizován rovnicí x =
f(x) a pro některé jednodušší funkce se dá spočítat explicitně. Také
se mu říká ekvilibrium, stacionární stav nebo pevný bod. Znalost
ekvilibria má velký praktický význam, protože můžete systém spustit
přímo z ustáleného stavu (a nemusíte se obávat, že by vám nějaké
bouřlivé transientní jevy roztrhaly třeba chemický reaktor).
V prostřední části obrázku je periodická orbita v zeleném (tady jsem to transientní chování už raději nezobrazil). V tomto případě je to série sedmi bodů, které funkce f postupně probíhá: f(x1) = x2, f(x2) = x3 a tak dále až po f(x7) = x1. Poslední iterace nás tedy vrátí do počátečního stavu a dál už se jen poskakuje po těch samých kamenech ve směru šipky (hezká animace je tady). Zda se při posledním skoku trefíte na první kámen, anebo ho o něco přeskočíte a budete tak dlouho kroužit dokola, až vytvoříte fialovou uzavřenou křivku z předchozího obrázku, je poměrně těžká otázka, která souvisí s aritmetickými vlastnostmi parametrů (viz např. Arnoldovy jazyky).
Ne vždy se ovšem nějaké ustálené asymptotické chování objeví. Pro určité hodnoty parametrů se při opakované aplikaci funkce objevují neustále nové a nové stavy, orbita nejeví žádné známky usazení a nahodile si poskakuje po množině X jako splašená kobyla (viz pravá část obrázku). Tyto případy obvykle zameteme pod veliký koberec, kterému říkáme Teorie chaosu.
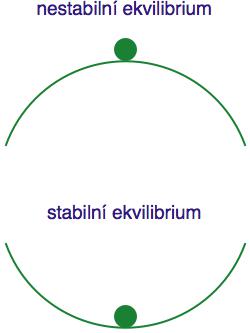
Velmi důležitou charakteristikou každého ekvilibria (pevného bodu) je jeho stabilita - tedy jak se dokáže vyrovnat s malým vychýlením. Nejlépe ji pochopíme ze schematického obrázku (vpravo). Na něm vidíme dvě kuličky - obě v rovnovážném stavu. Ta vrchní spočívá na konkávní podložce, a když do ní trochu strčíme, odkutálí se pryč (technicky: když malinko změníme počáteční hodnotu x(0), dynamika procesu odnese kuličku směrem od ekvilibria). Takovému ekvilibriu říkáme nestabilní.
Spodní kulička spočívá na konvexní podložce a platí pro ni přesný opak. Pokud ji vychýlíme z rovnovážné polohy, dynamika ji dokáže vrátit zpět. Toto ekvilibrium je tedy stabilní. Kdykoliv vystartujeme z jeho okolí, kulička se „sama o sobě“ dostane do původního stavu. V tom tkví praktický význam stabilních asymptotických stavů (ať jsou to ekvilibria nebo periodické orbity) - dají se poměrně snadno „objevit“ počítačovou simulací. Ty nestabilní se musí pracně spočítat z příslušných rovnic (pro ekvilibria: f(x) = x).
I proto jsem neměl problém vykreslit ekvilibrium v levé části předchozího trojobrázku. Prostě jsem si vzal náhodný počáteční bod, chvíli jsem tu Kanekovu funkci iteroval (to jsou ty modré body) a ekvilibrium se samo objevilo na talíři.
Z toho všeho vyplývá, že pokud chceme analyzovat diskrétní dynamické systémy, musíme v první řadě pochopit proces iterace funkce f, která diskrétní dynamiku řídí. A začneme jednorozměrným případem, který se dá pochopit i bez náročné simulace počítačem.
Iterace
Iterace je opakované provádění určité matematické operace nebo algoritmu.
Připomeňme si z minulých Matykání, že každá funkce je v podstatě malá skříňka s trpaslíkem, která má jeden vstup a jeden výstup. Při vykreslení grafu funkce vezmeme (alespoň v principu) nekonečně mnoho hodnot x z nějakého intervalu, hezky je jednu po druhé naházíme do vstupního otvoru funkce a pomocí výstupních hodnot y z nich složíme páry (x, y), které tvoří graf příslušné funkce. Důležité je, že každou hodnotu házíme na vstup pouze jednou.
Iterace dané funkce je v jistém smyslu sesterský proces, kdy si vezmeme pouze jednu hodnotu x, ale vhodíme ji do vstupu funkce nekonečně mnohokrát. Přesněji: hodíme ji na vstup a to, co nám vyleze na výstupu (funkční hodnota), opět hodíme do vstupního otvoru. A toto nekonečněkrát opakujeme.
Při iteraci funkce tedy de facto vytváříme následující posloupnost:
x, f(x), f(f(x)), f(f(f(x))), f(f(f(f(x)))), ...
Pokud si vypomůžeme indexovanými proměnnými (s tím, že položíme x0 = x), tak předchozí iterace vyjádříme takto:
x1 = f(x0)
x2 = f(x1)
x3 = f(x2) ...
V obou případech dostaneme tu samou posloupnost, která reprezentuje orbitu bodu x v dynamickém systému odpovídajícímu funkci f(x).
Tento algebraický přístup nám sice (ve spolupráci s počítačem) umožní si dynamiku systému poměrně rychle osahat, ale pro vnitřní pochopení toho, co se v systému děje, je dobré se na věc podívat i geometricky.
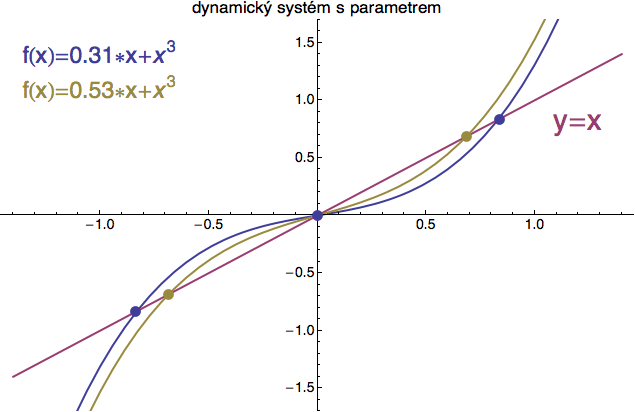
Na dalším obrázku vidíte jednorozměrný dynamický systém (X je reálná přímka), jehož dynamika F je určena iterací kubické funkce f(x) = rx + x^³, zde s parametrem r = 0.31. V tomto případě je dynamika poměrně jednoduchá. Pevné body si spočítáme přímo z rovnosti f(x) = x (což je po zkrácení kvadratická rovnice) a dostaneme tři kořeny označené fialovým kolečkem: k = 0.83, K = 0 a ten poslední -0.83 už na obrázku nevidíme. Tyto pevné body reprezentují ekvilibria našeho systému. Pokud si zvolíme za počáteční hodnotu x jeden z těchto kořenů, funkce f(x) je ponechá na místě - jak jí káže rovnice pro ekvilibrium.
Vezměme si teď počáteční bod x = 0.89, který leží těsně nad ekvilibriem. Když začnete funkci iterovat z tohoto bodu, dostanete geometricky zelený klikyhák naznačený na obrázku (kdykoliv se zelená lomená čára dotkne modré funkční křivky, máme další iteraci). Takto si můžete představit celou posloupnost x1, x2, x3, x4, .... Fialová křivka y = x je tam de facto jen proto, abychom mohli snadněji přesunout výstup funkce na vstup. Pokud se chcete dynamikou vážně zaobírat, je dobré si metodu „zelených klikyháků“ osvojit.
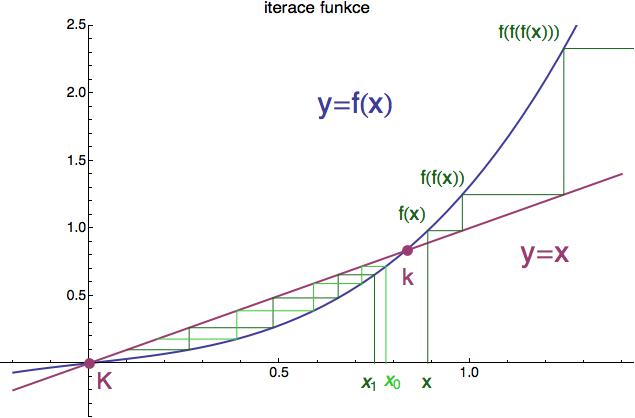
Pokud si to rozmyslíte, tak z obrázku vyplývá, že kdykoliv si zvolíte
počáteční bod x nad fialovým ekvilibriem k = 0.83, příslušná orbita
(trajektorie) odkráčí do nekonečna. To je z geometrie přímo
vidět a nemusíte kvůli tomu trápit počítač.
Zcela jiná situace ale nastane, pokud si zvolíte počáteční hodnotu x0 těsně pod ekvilibriem. Iterace funkce nás pak zavede (v asymptotické limitě) do prostředního ekvilibria K = 0, jak ukazuje světle zelený klikyhák. A to platí pro kterýkoliv počáteční bod z intervalu (0, k). Na obrázku je vyznačen ještě jeden: x1. I jeho orbita se asymptoticky blíží k bodu K = 0, i když podél jiné trajektorie.
Z téhož obrázku také vidíme, že pevný bod k = 0.83 reprezentuje nestabilní ekvilibrium (stačí malá změna počáteční hodnoty a iterace nás odnese pryč!), zatímco pevný bod K = 0 reprezentuje stabilní ekvilibrium. Když vystartujeme z nějakého bodu na ose x, kousek vlevo nebo vpravo od tohoto ekvilibria, iterace nás vrátí zpátky - přesně jako na schematickém kuličkovém obrázku výše.
Jednu z možností, jak takovou dynamiku znázornit, představuje Juliova množina (známá milovníkům fraktálů). Představme si, že počáteční podmínky x, pro které iterace neutečou do nekonečna, označíme černou barvou - to budou všechny body z intervalu (0, k). Naopak počáteční hodnoty x > k, které funkce f při iterování „odfoukne“ do nekonečna, si označkujeme nějakou barvou zhruba odpovídající počtu iterací potřebných k překročení předem zvoleného vysokého čísla (řekněme 1000). To, co na reálné ose potom dostaneme, bude jednorozměrný analog Juliovy množiny pro funkci f(x). V tomto případě to bude množina vizuálně jednoduchá: interval (0, 1) bude černý a zbytek kladné poloosy x bude barevný. Když si ovšem tutéž konstrukci provedete ve dvou dimenzích (nejlépe pomocí komplexních funkcí), dostanete pozoruhodné dvourozměrné obrázky s velmi jemnou až fantaskní strukturou.
A teď zpátky na bojiště, kde se situace mění každým okamžikem.
Obě dosud zmíněné funkce - jednorozměrná kubická z této sekce i trojrozměrná kvadratická ze sekce předchozí - v sobě obsahovaly určité parametry. Samozřejmě pokud tyto parametry změníme, změní se i dynamika celého systému. Takto tedy matematika reaguje na svět, který je v neustálém pohybu. Do svých rovnic si zamontuje parametry jako měnící se „simulátory reality“. Co platilo včera, dnes už neplatí.
Na dalším obrázku jsem si vzal stejnou kubickou rovnici f(x) = rx + x3, ale hodnotu parametru r jsem zvýšil na r = 0.53. Vidíte, že kvalitativně se nic nezměnilo - stále máme stabilní ekvilibrium uprostřed a dvě nestabilní ekvilibria po stranách (můžete si to ověřit pomocí zelených klikyháků). Změnily se ovšem kvantitativní vlastnosti systému. Zatímco stabilní ekvilibrium zůstalo v nule, obě nestabilní ekvilibria se trochu posunula: do bodů 0.685 a -0.685.
Když si to trochu rozmyslíte, zjistíte, že pevné body budou stabilní,
pokud má derivace v tom bodě absolutní hodnotu menší než jedna (tj. funkce f protíná osu y = x shora dolů) a nestabilní v opačném případě - tedy
pokud absolutní hodnota derivace v bodě ekvilibria splňuje: |f'(x)| >
1.
Občas se ale stane, že i malý posun v parametrech systému změní jeho dynamiku kvalitativně. Tedy např. že změní počet jeho ekvilibrií, popřípadě jejich stabilitu. Nebo se nám dokonce objeví (ve více dimenzích) uzavřené křivky. V takovém případě říkáme, že v systému došlo k bifurkaci.
Bifurkace
Bifurkace je tedy kvalitativní změna chování dynamického systému způsobená přechodem parametru přes nějakou kritickou hodnotu.
Podívejme se na to nejprve v jednorozměrném případě. Tentokrát si kubickou funkci vykreslíme pro hodnotu parametrů r = 0.53 a r = 1.29
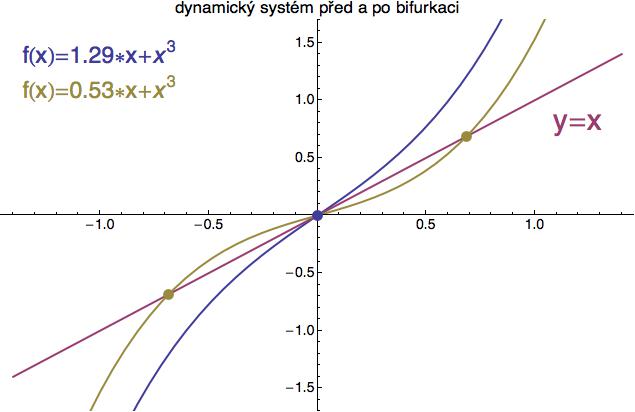
Z tohoto obrázku vidíte (a můžete si to opět ověřit zelenou
klikyháko-analýzou), že modrá funkce má jedno nestabilní ekvilibrium v bodě x = 0. Béžová funkce má ale o dvě ekvilibria více. Někde mezi r =
1.29 a r = 0.53 tedy leží hodnota r, při které dojde k bifurkaci - v tomto
konkrétním případě bod x = 0 získá stabilitu a současně se z něj
oddělí dvě nestabilní ekvilibria, naznačená béžovými body, která při
dalším zmenšování r odplují do dáli. Když si s tím budete hrát,
zjistíte, že k bifurkaci dojde pro r = 1, kdy bude mít funkce f(x) v bodě x = 0 derivaci rovnou přesně jedné (tehdy bude v nule přesně kopírovat
přímku y = x).
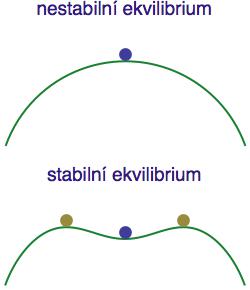
Abychom to snadněji vstřebali, představme si tuto bifurkaci opět schematicky pomocí malého míčku na vypouklé (konkávní) podložce, která bude zastupovat funkci f (viz obrázek vpravo).
Nahoře vidíme situaci těsně před bifurkací. Systém má jedno nestabilní ekvilibrium (přesně tam, kde sedí modrý bod) a pokud do něho z kterékoliv strany drkneme, kulička uteče pryč (sjede s kopce). Místo poněkud abstraktní manipulace s parametrem funkce f si změnu dynamiky můžeme představit tak, že do zelené podložky shora zatlačíme prstem, čímž ji prohneme do tvaru znázorněného na spodním obrázku. V bodě 0 je stále ekvilibrium, ale najednou získalo stabilitu. Teď můžeme do kuličky klidně drcnout a ona se nám vrátí zpět. Současně s touto změnou stability se v systému objevila dvě nová nestabilní ekvilibria v bodech, kde sedí dvě béžové kuličky. Dynamika systému tedy doznala kvalitativní změny - máme tři ekvilibria namísto jednoho.
Tomuto typu bifurkace se říká „vidlová“ (pitchfork bifurcation), protože ekvilibrium se vlastně roztrojí - stejně jako konec známého zemědělsko-revolučního nástroje. Tato bifurkace má ještě zrcadlového dvojníka, kdy původně stabilní ekvilibrium tuto stabilitu ztratí a z něho se „odloupnou“ dvě nová stabilní ekvilibria (obrázek pak vypadá stejně jako ten předchozí - jen je otočen vzhůru nohama).
Protože změna parametru dokáže změnit dynamiku daného systému, můžeme si vytvořit ještě jiný typ fraktálu. Nejprve si zafixujeme počáteční hodnotu, řekněme x = 0, a budeme ji iterovat pomocí funkce s měnící se hodnotou parametru (v našem případě r). Na reálné přímce potom obarvíme každý bod r podle toho, zda iterace bodu x = 0 funkcí odpovídající tomuto parametru odběhne do nekonečna, a nebo ne. Tímto způsobem získáme tzv. Mandelbrotovu množinu (a nejlepší je opět se na ni dívat ve dvourozměrném případě optikou komplexních čísel).
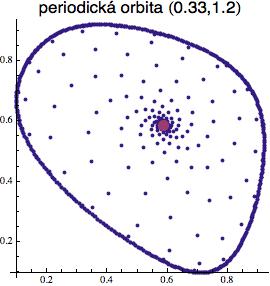
Vidlová bifurkace ale zdaleka není jedinou kvalitativní změnou dynamiky, se kterou se v praxi setkáváme. Vezměme si např. třírozměrný Kanekův systém popsaný výše: zafixujme si v něm a = 0.33 a hodnotu c budeme postupně zvyšovat z 0.8 na 1.2 (a za počáteční bod si zvolíme počátek (0, 0, 0)). Ze začátku bude náš systém konvergovat ke stabilnímu ekvilibriu, které ovšem někde kolem hodnoty c = 1 ztratí stabilitu a odloupne se z něj stabilní uzavření křivka (podél níž pak orbita hopsá) - viz obrázek vpravo.
Původní ekvilibrium tam stále je (fialově) a můžete si ho klidně spočítat - výpočtem zjistíte, že má pro c = 1.2 hodnotu (0.5868, 0.5868, 0.5868). Ale už se k němu nedostanete dynamickou iterací, protože je nestabilní. Pokud si nastartujete dynamický systém z nějaké počáteční hodnoty poblíž ekvilibria, příslušná modrá orbita (trajektorie) se bude sice chvíli šmrdlat v okolí tohoto bodu, ale pomalu se od něj odkutálí (stejně jako kulička na schematickém obrázku) a nakonec se „navine“ na stabilní uzavřenou křivku, kterou vidíme na obrázku.
Tomuto typu bifurkace, kdy se při přechodu parametru přes nějakou kritickou hodnotu ze stabilního ekvilibria oddělí stabilní uzavřená křivka, se říká Hopfova bifurkace.
A do třetice všeho dobrého se zmíním o bifurkaci zdvojené periody. Ta funguje velmi podobně jako „zrcadlová“ verze vidlové bifurkace. Původně stabilní ekvilibrium x změnou parametru stabilitu ztratí a na jeho místo nastoupí dvojice bodů x1 a x2. Jediná změna spočívá v tom, že zatímco u vidlové bifurkace jsou oba nové body také ekvilibria - tedy splňují
x1 = f(x1) a současně x2 = f(x2)
u zdvojovací bifurkace je nový pár periodickou orbitou (perioda 2) splňující
x1 = f(x2) a současně x2 = f(x1)
(funkce f tedy tyto dva body vzájemně prohazuje)
Zajímavé na této bifurkaci je, že i tento nový pár záhy ztratí stabilitu a tu převezme nová orbita s periodou 4 (každý z těch dvou bodů se tedy rozdvojí). A to zdvojování pokračuje dál přes periodu 8, 16, 32 až do nekonečna. Bifurkace ale probíhají stále rychleji (mezery mezi bifurkačními hodnotami parametru se zkracují) a nakonec vyústí v chaos, kdy orbita vypuštěná z dané počáteční podmínky žádné ustálené chování nenalezne.
Schematicky to vidíte na následujícím obrázku pro tzv. logistickou funkci
f(x) = rx(1-x)
Na vodorovné ose bude parametr r a na svislou osu si vyneseme všechny hodnoty stabilní periodické orbity, která pro tu hodnotu existuje. Prakticky si ten obrázek vyrobíte tak, že z pevné počáteční hodnoty x (a zde jsem si vzal x = 0.6) nejprve spočítáte 10000 iterací, z nichž prvních 9000 zahodíte, abyste se zbavili transientních jevů, a dalších 1000 iterací si uchováte v paměti a pro příslušnou hodnotu r je vykreslíte na ose y (ze začátku je to jen jeden, dva nebo čtyři body, ale se zvyšujícím se r objevíte i komplikovanější a neustálené orbity).
Vidíte, že k první zdvojovací bifurkaci dochází pro r = 3, ke druhé zhruba pro r = 3.45 a pak už to jde ráz na ráz a zhruba kolem hodnoty r = 3.6 vypukne chaos (přesněji: objeví se komplexnější orbity).
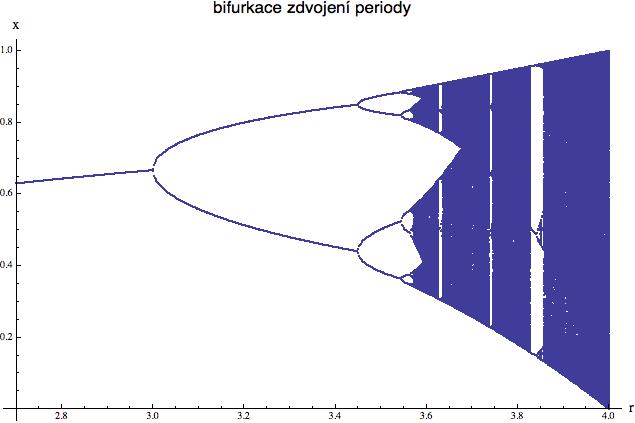
Tento obrázek najdete prakticky v každé učebnici dynamických systémů.
Článek je redakčně upravenou verzí blogového příspěvku na serveru
iDNES.cz. Publikováno s laskavým svolením autora.
Další díly a původní texty jsou dostupné na blogu Jana Řeháčka.




