Matykání: Na kvantové hůrce

Dnes si uděláme malý výlet do bizarního světa kvantové mechaniky. Nebudeme se snažit pochopit, jaké zvláštní zákonitosti v tomto mikroskopicky zavinutém světě panují, ale podíváme se, jakou matematikou se je fyzika pokouší popsat.

(toto Matykání volně navazuje na článek o nekonečné dimenzi)

Teorie matic se rozvíjela především v souvislosti se studiem vlastností lineárních zobrazení mezi konečně rozměrnými vektorovými prostory. S maticemi sice můžete pracovat i bez tohoto náhledu, ale pokud chcete pochopit jejich vnitřní mechaniku, je to nejnázornější cesta.

Před časem jsme ale viděli, že mohou existovat i prostory, jejichž dimenze je nekonečná. V tomto případě se pak zobrazením říká operátory a jejich studiem se zabývá funkcionální analýza. Velkou zásluhu na jejím rozvoji má kvantová mechanika, která se v první polovině 20. století potřebovala nějak kvantitativně vyrovnat se zcela novou fyzikální realitou. A ukázalo se, že zobecnění, která funkcionální analýza poskytovala, jsou přesně tím pravým ořechovým, co nová teorie potřebovala k popisu reality na úrovni elementárních částic.

A to rozhodně není realita, na kterou by se dalo jít selským rozumem. Představte si, že vyšlete golfový míček proti zvlněné překážce. Pokud míček nebude mít dostatečnou rychlost (tedy kinetickou energii), vlnu prostě nepřeleze a vrátí se vám k nohám. Kvantový míček tu bariéru zdolat dokáže, i když nemá dostatečnou energii (viz kvantové tunelování). No dobrá, podrbete se za uchem a vezmete míček ke druhé jamce, kde musí projít jedním ze dvou otvorů ve stěně. Jenže ten šibal míček si klidně protančí oběma dírami současně. A když ho začnete nenápadně pozorovat, zjistíte, že čím podrobněji jste si do notýsku zaznamenali jeho polohu, tím větší chybka se vám vloudila do odhadu jeho rychlosti, takže nakonec víte kulový. Zanesete tedy rozhořčeně míček ke správci na kalibraci a on vás s koženým úsměvem upozorní, že výsledky tohoto měření mohou ovlivnit vlastnosti podobného míčku kdesi v galaxii Arkana, kde se jej právě chystá odpálit tamní král Marťan IV. Takže sorry. No a cestou domů vám ho ještě spolkne Schrödingerova kočka a přivolaný zvěrolékař je nucen konstatovat, že se jím ta potvora žravá současně udávila i neudávila.

Pojďme se tedy podívat, jaký typ matematiky budeme potřebovat, abychom tento prapodivný svět zkrotili.

Operátory

Protože matematika studuje vztahy mezi různými jevy, jedním z jejich fundamentálních nástrojů je funkce, která vyjadřuje závislost mezi dvěma veličinami.

Kdysi na začátku jsme si funkci představili jako skříňku s trpaslíkem (obr. vpravo), do které vhodíme vstupní veličinu x, trpaslík ji nějakým způsobem transformuje – obvykle tak, že hodnotu x dosadí do nějakého vzorečku – a na výstupu nám pak vyhodí výslednou funkční hodnotu y. Tento proces zapisujeme v tradičním formátu jako y = f(x), ale občas se setkáme i s alternativami, např.:

f: x --> y

který o něco lépe vyjadřuje skutečnost, že funkce f zobrazuje hodnotu x na y. Pro většinu funkcí, se kterými se v praxi setkáte, jsou hodnoty x a y prostě reálná čísla.

Koncept funkce je ale daleko univerzálnější a do některých skříněk můžeme vhazovat i komplikovanější objekty (takže vstup a výstup pak svazuje komplikovanější jevy). Na vysoké škole narazíte na funkce více proměnných, kdy do skříňky vhodíte několik hodnot (tedy de facto vektor) a na výstupu si vyzvednete funkční hodnotu (ta bude prozatím stále pouze číslem), např. f(x,y) = x² + 3y.

Pro ještě zapařenější procesy můžeme použít funkce, do kterých vhodíme vektor u a na výstupu nám vypadne jiný vektor, v = F(u).

Představte si například, že chcete modelovat gravitační pole kolem Země. K takovému popisu budete potřebovat funkci, do které jeden vektor vhodíte (poloha, kde vás to gravitační pole zajímá) a jiný vektor vám vypadne (gravitační síla v tom bodě): g = G(r). Takovým funkcím říkáme vektorové pole.

Prakticky stejný typ funkce ale můžeme použít i pro popis geometrických transformací (například rotace či zrcadlení), kdy do funkce vhodíme vektor u, který chceme transformovat, a na výstupu nám ze skříňky vypadne výsledný vektor v (např. pootočený či zrcadlový obraz vektoru u). V tomto případě se té funkci říká transformace.

Při troše dobré vůle se skříňka dá zkonstruovat tak, že se do ní dá vhodit prakticky všechno. Například Jára Cimrman kdysi zkonstruoval funkci, do které se dá vhodit prošlé máslo a na výstupu vám vyleze cihla.

Není tedy důvod, proč bychom nemohli zkonstruovat skříňku, do které můžeme vhodit i funkce, což – jak jsme viděli před časem – jsou vektory z nějakého abstraktního nekonečně-rozměrného prostoru a na výstupu nám pak vypadnou jiné abstraktní vektory (obvykle ze stejného prostoru – ale to není podmínkou, klidně můžeme nazpátek dostat i čísla). Těmto „funkcím na funkcích“ říkáme operátory a ty tvoří páteř matematického popisu kvantové mechaniky. Matice jsou speciálním případem operátorů na konečně rozměrných prostorech.

Názvosloví není úplně ustálené a mnoho autorů používá slova „operátor“, „matice“ a „transformace“ téměř jako synonyma. Pokud se s nějakými komplikovanějšími funkcemi setkáte, vždy se přesvědčte, jaký typ objektu do funkce vhazujete a co vám vypadává na výstupu. V tomto Matykání bude operátor prostě funkce z jednoho obecného vektorového prostoru do druhého s tím, že většinou budeme mít na mysli (nekonečně-rozměrný) prostor funkcí.

Abychom si to trochu osahali, tady jsou na ukázku tři typy operátorů.

1. Asi nejjednodušším příkladem operátoru je násobek

Vezmeme si nějakou pevnou funkci, třeba p(x) = x², a operátor pak definujeme tak, že každou vstupní funkci pronásobíme tou pevnou:

P: f(x) --> p(x) * f(x)

Pokud tedy do skříňky vhodíme funkci sin(x), na výstupu nám vypadne funkce x²sin(x)

2. Na derivaci (resp. proces derivování) se můžeme také dívat jako na operátor

Kdysi dávno jsme viděli, že ke každé dostatečně hladké funkci f(x) se dá najít sekundární funkce f'(x), říkáme jí derivace funkce f, která vyjadřuje, do jaké míry primární funkce f(x) v každém bodě x klesá či stoupá. Proces derivování, kdy z primární funkce pomocí určitých pravidel vytvoříme sekundární funkci f, je tedy také operátorem.

D: f(x) --> f'(x)

Ale pozor, nepleťte si diferenciální (derivační) operátor D s výstupní hodnotou (tedy derivací f'). Do operátoru D vhodíme funkci f a na výstupu nám vyleze funkce f'. A to už je běžná reálná funkce, do které vhodíme x a na jejím výstupu nám vyleze číslo y = f'(x), udávající směrnici tečny k primární funkci f(x) v bodě x.

(operátor je tedy pořádná skříň, do které vhazujeme menší skříňky a na výstupu nám pak vypadávají jiné menší skříňky – což je docela na skříňku, tedy chci říci na bednu)

3. Otrlé povahy si mohou složitější typ operátoru nabrnkat pomocí integrace

Vezmeme si nějakou funkci dvou proměnných na jednotkovém čtverci, třeba k(x,y), a pro každou vstupní funkci f pak definujeme operátor takto:

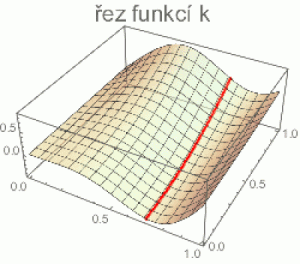
K: f(x) --> ∫k(x,y)f(y) dy

Pro pevné x je první člen vpravo pouze funkcí proměnné y (viz ilustrace), takže celá ta hrůza je (v prostoru funkcí) skalárním součinem funkce f a červeného „řezu“ funkce k (pro pevné x). Výsledkem této operace je číslo z definované pravou stranou (tím integrálem se nenechte zastrašit, to je pouze spojitá verze součtu přes hodnoty y). Je to jako Cimrmanův řez postelí a peřinou. Jak měníme hodnotu x (která nám udává polohu řezu), mění se i červený tvar řezu (křivka peřiny) a tím pádem i čísla z. A tímto zobrazením je definována naše výstupní funkce:

Kf: x --> z
(zde je K ta velká skříň, f ta malá vstupní skříňka a Kf ta výstupní)

Funkci k(x,y), která de facto celou operaci diriguje, říkáme jádro integrálního operátoru K (kernel). Pokud se vám teď kouří z makovice, tak se neděste, to se stává zcela běžně.

Jako první nás u běžných funkcí obvykle zajímá definiční obor. Tedy jaké hodnoty x lze do skříňky vhodit, aniž bychom narušili matematická pravidla (u reálných funkcí např. nesmíme dělit nulou či odmocňovat záporné číslo).

U operátorů je otázka definičního oboru ještě o něco složitější, protože pravidel, která lze narušit, je více. Například u diferenciálního operátoru D musíme zaručit, že pro funkci f, kterou do skříňky vhazujeme, se dá směrnice tečny T (tj. derivace) spočítat v každém bodě x. Jinak trpaslík vyběhne a majzne nás baseballovou pálkou B po hlavě H.

Proto má matematika poměrně rozsáhlý katalog různých funkčních prostorů, jejichž vlastnosti zaručují, že ten či onen operátor je správně definován. V kvantové mechanice se nejčastěji setkáme s prostorem funkcí L², což jsou zhruba řečeno funkce, pro něž lze vyčíslit integrál ze čtverce dané funkce ∫f² (to není překvapivé, uvážíme-li, že velikost běžných vektorů se spočítá součtem čtverců souřadnic a následným odmocněním – a integrál je v podstatě spojitý součet – i zde tedy cílíme na to, aby naše funkce neboli abstraktní vektory měly konečnou velikost neboli normu).

Důležitou kategorií jsou lineární operátory L, splňující podmínky

(P1) L(f + g) = L(f) + L(g)
(P2) L(tf) = tL(f)
pro každý skalár t a pro každou dvojici funkcí f a g z daného funkčního prostoru.

Výše uvedené operátory P, D a K jsou lineární. U prvního si to lehce ověříte sami, u dalších dvou to plyne ze základních vlastností diferenciálního a integrálního počtu.

Jen bych zdůraznil, že nás zajímá linearita operátoru L, nikoliv to, zda jsou vstupní či výstupní funkce lineární samy o sobě. Zadejme si např. operátor L pomocí násobení

L: f(x) --> x²f(x)

a za konkrétní funkce si vezmeme f(x) = sin(x) a g(x)=cos(x).

Dostaneme následující výstupní funkce

L(f) = x²sin(x)
L(g)= x²cos(x)
L(f + g)= x²(sin(x) + cos(x))

a vidíme, že podmínka P1 platí (podobně platí i P2). Operátor L je tedy lineární, přestože f(x) i g(x), a koneckonců i x², jsou vesměs nelineární funkce.

A konečně – stejně jako u matic – nás budou zajímat vlastní čísla a vlastní vektory (a protože tady to jsou funkce, často jim říkáme vlastní funkce či vlastní stavy). Tedy případ, kdy nějakou funkci vhodíme do skříně a na výstupu nám trpaslík vyhodí tu samou funkci, jen pronásobenou nějakým skalárem t. Tomu skaláru pak říkáme vlastní číslo (náležící příslušné vlastní funkci).

L(f) = tf (nebo chcete-li tam vidět i proměnnou: L(f(x)) = tf(x))

Vlastní vektory (či vlastní funkce) jsou tedy speciální případy, kdy lze výstupní funkce operátoru obdržet z těch vstupních pouhým přeškálováním. Jinými slovy, to, co ze skříňky vyleze, má stejný „směr“ jako to, co jsme tam hodili (i když pojem „směru“ se hodí spíše pro vektory než pro funkce). To je dosti svazující podmínka a ty kouzelné „směry“ se proto musí poměrně pracně hledat. Drtivá většina vektorů, které do skříňky vhodíte, vyleze směrově „pootočená“.

V kvantové mechanice hrají takové invariantní „směry“ klíčovou roli.

Analýza spektra je pro nekonečně rozměrné operátory pochopitelně o něco komplikovanější než pro matice. Předchozí rovnice se dá zapsat jako (L - tI)f = 0, kde I je identický operátor, či zkráceně (L - t)f = 0. A to znamená, že inverzní operátor (L - t) ^-1 se nedá dobře definovat (zobrazoval by 0 do nenulové funkce f a to pro lineární operátory není kvůli podmínce P2 možné). Pro matice tím výčet patologií operátoru (L - t) ^-1 končí. V nekonečné dimenzi však mají operátory podstatně více možností si zalumpačit. Inverzní operátor např. může být definován, ale nemusí být omezený, tj. může jednotkovou kouli zobrazit na neomezenou množinu (to by matice nikdy neudělala!). V důsledku toho je spektrální analýza na Banachových či Hilbertových prostorech velmi delikátní záležitost).

Kvantová mechanika

Nejprve stručné opáčko mechaniky klasické.

Stav nějakého fyzikálního systému, třeba letícího pingpongového míčku, je v zásadě popsán dvěma 3D vektory (r,v), kde r je polohový vektor a v je vektor momentální rychlosti (či hybnosti – po pronásobení hmotou). To, že je stavový prostor de facto šestirozměrný, by nemělo být velké překvapení. K tomu, abychom mohli předpovědět budoucí trajektorii míčku, musíme znát 6 čísel – tři souřadnice, které nám prozradí, kde míček je, a další tři, které nám řeknou, kam má namířeno. Jakmile máme stav zafixován, můžeme zkoumat další měřitelné veličiny, např. energii, která bude v té nejjednodušší podobě dána výrazem E(r,v) = V(r) + mv²/2, kde první člen reprezentuje potenciální energii (závislou na poloze) a druhý kinetickou energii (závislou na rychlosti: v je zde norma vektoru rychlosti v).

Měřitelné veličiny jsou spojitými funkcemi stavových veličin a to znamená, že mohou nabývat všech možných hodnot (v rámci určitých fyzikálních mantinelů). Fyzikální veličiny můžeme v principu měřit s libovolnou přesností a z nich můžeme deterministicky určit vývoj celého vesmíru.

Kvantová mechanika funguje zcela jinak. Jedním z jejich pilířů je dualita popisu prostřednictvím vln a částic, takže na mikroskopické úrovni mají materiální objekty též charakter (a vlastnosti) vln, resp. vlnového šíření. Jejich dynamiku si tedy velmi zhruba můžete představit jako vlnu šířící se po hladině rybníka, když do něj hodíte kámen. A ta vlna je současně trochu tady, ale taky trochu támhle – a možná už i trochu v rákosí.

Stav systému je v tomto případě popsán tzv. vlnovou funkcí ψ(x), která nabývá komplexní hodnoty a v podstatě udává pravděpodobnost, že se daný systém – obvykle nějaká elementární částice – nalézá v okolí bodu x (někdy se jí říká komplexní či pravděpodobnostní amplituda).

Vlnové funkce jsou samozřejmě součástí funkčního prostoru, kterým je ve většině případů vhodný komplexní Hilbertův prostor. Díky tomu se v něm pro každé dvě funkce ψ a φ dá definovat skalární součin (ψ,φ), který fyzici od dob Diracových značí <ψ|φ> s tím, že první funkci říkají bra a té druhé ket, takže to dohromady vytvoří anglické slovo pro závorku: bracket (tato notace zohledňuje rozdíl mezi vektory |ket> a kovektory <bra|, ale s tím si nebudeme na této úrovni lámat hlavu). Důležité je, že díky skalárnímu součinu můžeme ve funkcionální analýze používat geometrickou intuici a metody běžné v eukleidovské geometrii (pojem délky, úhlu atd.), přestože stavový prostor nabobtnal z šesti do nekonečně rozměrného média.

Z pohledu matematiky jsou zde ale dva zásadní rozdíly. Zatímco klasická mechanika je deterministická a opírá se o strukturu reálných čísel, kvantová mechanika je pravděpodobnostní a velmi zásadním způsobem využívá komplexní čísla (bez íčka se vám kvanta zkrotit nepodaří).

To znamená, že se neptáme, zda je částice tady anebo tamhle, ale jaká je pravděpodobnost, že je zrovna v tomhle kousku prostoru. A protože pravděpodobnost je reálná veličina, pravděpodobnostní hustota je daná čtvercem absolutní hodnoty vlnové funkce

p(x) = |ψ(x)|²
Čím vyšší p, tím pravděpodobněji se částice nalézá poblíž x.

Technicky vzato: pravděpodobnost P, že se částice nalézá v nějaké konkrétní oblasti O pak dostaneme integrací hustoty p přes oblast O.

P = ∫|ψ(x)|² dx

Proto používáme výše zmíněný prostor L², aby s tím integrálem nebyly potíže. Pokud nevládnete integrálním počtem, představte si prostor diskretizovaný do nějaké mřížky (šachovnice) a ten integrál je pak spojitou verzí prostého součtu pravděpodobností přes všechna políčka.

Částice se ale někde nalézat musí, a proto se celková pravděpodobnost (přes celý prostor) musí rovnat 1. Vlnové funkce jsou tím pádem normalizované (jejich celkový integrál je 1). Jinými slovy, pokud se dvě vlnové funkce liší pouze o skalární násobek, popisují ten samý stav (to znamená, že vlnové funkce si vegetí v projektivním prostoru, který jsme nedávno zkoumali).

A teď to nejdůležitější. Měřitelné veličiny (observables) odpovídají lineárním operátorům na Hilbertově prostoru, ze kterého vlnové funkce vybíráme (ten se může problém od problému lišit). Na rozdíl od klasické mechaniky, kde můžete naměřit prakticky libovolné hodnoty, v kvantové verzi naměříte pouze hodnoty odpovídající vlastním číslům příslušného operátoru (toto je jeden z důvodů, proč je kvantová mechanika ve své podstatě diskrétní, zatímco ta klasická je spojitá). A aby toho nebylo málo, po měření se stav systému skokově změní na vlastní funkci odpovídající naměřenému vlastnímu číslu (tomuto poměrně mystickému procesu se říká kolaps vlnové funkce). Něco takového by v klasické mechanice okamžitě vyvolalo skandál.

Operátory navíc vykazují určitou formu symetrie (říkáme jim hermitovské), díky které jsou jejich vlastní hodnoty reálné a jejich vlastní funkce (vektory) tvoří ortonormální bázi příslušného Hilbertova prostoru. Díky tomu dokážeme i z kvantových systému vyždímat měřením reálná čísla a z vlastních vektorů pak kombinacemi složíme celý prostor.

Jak jsem ale předeslal, celý proces je pravděpodobnostní. Rozepišme si vlnovou funkci pomocí báze z vlastních vektorů (funkcí) daného operátoru. Toto je v podstatě sofistikovanější verze rozkladu síly do lineárně nezávislých směrů.

ψ = a1 ψ1 + a2 ψ2 + ... + ai ψi + ...
(kde ψi jsou vlastní funkce a ai komplexní koeficienty)

Pokud se systém nachází ve stavu odpovídajícímu jedné z těch vlastních funkcí, řekněme ψ2, pak naměříme příslušnou vlastní hodnotu λ2 (nikoliv a2 – to je pouze jeden z koeficientů rozvoje) se stoprocentní pravděpodobností.

Koeficienty ai nám vyskočí jinde.

Je-li systém v obecném stavu ψ (daném kombinací neboli superpozicí všech vlastních funkcí), jak je naznačeno v předchozí sumě, pak bude naměřena hodnota odpovídající náhodnému výběru z vlastních čísel λi, přičemž i-té číslo bude z kvantového osudí vytaženo s pravděpodobností pi danou výrazem (Bornovo pravidlo).

pi = |<ψi | ψ>|²

(A to jsou de facto čtverce koeficientů rozvoje ai; jen mějte na paměti, že všechny ty roztomile vyhlížející skalární součiny jsou v případě funkcí definovány integrálem.)

A protože různé měřitelné veličiny mají v principu různé vlastní vektory (resp. funkce), nemůžeme všechny veličiny měřit současně s libovolnou přesností – což je obsahem známého Heisenbergova principu neurčitosti.

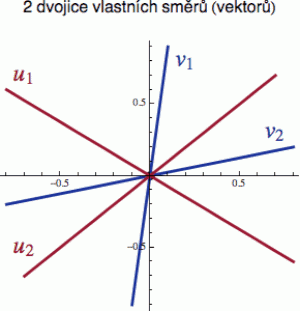
Zjednodušeně si to můžeme představit takto: Měříme dvě veličiny, které mají dvě různé dvojice vlastních vektorů (na obr. vpravo naznačené červeně a modře). V okamžiku, kdy změříme červenou veličinu, se stav systému změní na jeden z červených vektorů u. Z pohledu modrých vektorů v pak bude systém v superpozici (každý z červených směrů se dá napsat jako kombinace modrých a naopak) a příslušné měření nám vydá svědectví o modrých hodnotách pouze s určitými pravděpodobnostmi (a ty jsou pochopitelně vydatným zdrojem neurčitosti). Se stoprocentní pravděpodobností bychom modré hodnoty naměřili pouze, pokud by se červené a modré vektory překrývaly.

Další možností, jak princip neurčitosti matematicky uchopit, je Fourierova analýza – k ní se snad propracujeme někdy v budoucnosti.

Časový vývoj vlnové funkce mezi jednotlivými měřeními popisuje tzv. Schrödingerova rovnice. Ta je v podstatě kvantovým ekvivalentem druhého Newtonova zákona, který říká, že derivace hybnosti (tedy její změna s časem) je úměrná působící síle – což vede ke známému středoškolskému F = ma. Schrödingerova rovnice ukazuje obdobně (ale komplikovanějším způsobem), jaká je časová derivace vlnové funkce.

Z pohledu matematiky je tedy kvantová mechanika z velké části spektrální analýzou operátorů na Hilbertově prostoru. A výpočetně funguje nadmíru dobře. To pravé dobrodružství spočívá v interpretaci, jak si celý ten abstraktní aparát správně fyzikálně vyložit. Pokud je mi známo, zde ještě mezi fyziky nepanuje úplná shoda.

Literární shrnutí: Krvavý Džejk se nenuceně opíral o hrubě otesané zábradlí verandy a s pobaveným úsměvem sledoval neohrabané pokusy svého nového parťáka přesunout balíky sena z bryčky na podlážku staré opršelé stodoly. Pomalu si balil cigaretu a v koutcích mu neznatelně zacukalo, kdykoliv se vidle novopečeného kovboje zapíchly do nosného trámu půdičky. Nemotora se jmenoval John Amos a jako většina zelenáčů dorazil na Divoký západ z Uhlazeného východu, konkrétně z Pensylvánie. Nosil nemožné kalhoty z manšestru a kolem krku měl uvázaný šátek, jehož jasně žlutá barva signalizovala na dálku několika mil, že těsně nad ním se nalézá hustý a lehce dostupný skalp. „Hej, Johne, nech toho popichování půdičky a pojď mi pomoct s rozvozem krmení," houkl Džejk na svého pomocníka. „Máme tu kvanta píce a musíme ji rozdělit kravám."

„Jaká kvanta?“ ozvalo se z obrovského chomáče sena nabodnutého na vidle. „Támhleta kvanta a taky támhleta a támhleta,“ objevovala Džejkova natáhnutá paže zdánlivě nevyčerpatelné zdroje úmorné lopoty, rozseté nepravidelně po celém pozemku. „A hlavně támhle nahoře, tam jsou kvanta veliká jako dospělý bizon,“ ukázal na úhledný stoh krmiva na malé ħůrce, které se pro její vyvýšenou polohu říkávalo ‚sněħůrka‘. Pověrčivější farmáři se dokonce dušovali, že tam za dlouhých zimních večerů rejdí sedmero trpaslíků, kteří do zasněžených plání kreslí podivné symboly a provozují jakousi obskurní magii. „Tak šup šup, kravám už určitě kručí v žaludku,“ pobízel netrpělivě Džejk. Ze stodoly se vyvalil oblak prachu a v něm jasně zasvítil žlutý šátek. „Všeliké to kvantování toliko pro hovada dobré jest,“ zahuhlal pod nesmělými vousy John Amos a cestou k ħůrce si několikrát mazácky odplivl, jako by ve Wyomingu žil již nejméně pět let.

Poloha a hybnost
(jen pro mimořádně otrlé povahy)

Pro operátory na konečně rozměrných prostorech (matice) je výpočet vlastních čísel a vektorů vcelku jednoduchý. Vyřeší se nějaká polynomiální rovnice a výsledek se dosadí do příslušné homogenní soustavy. V nekonečné dimenzi je takový výpočet hotovou džunglí a prosekání cestičky si často vyžaduje speciální mačety vypůjčené z ostatních matematických disciplín.

Podívejme se pro ilustraci na kvantové pojetí polohy a hybnosti.

Operátor polohy X je definován předpisem

X: ψ(x) --> x * ψ(x)

Je to tedy operátor prvního typu, kdy do skříňky hodíme nějakou funkci ψ a trpaslík ji prostě pronásobí proměnnou x. Vlastní číslo x° (a příslušná vlastní funkce ψ°(x)) musí splňovat rovnici

x.ψ°(x) = x°.ψ°(x)

a to znamená, že (x-x°) ψ°(x) = 0, pro každé x z definičního oboru.

Je-li x ≠ x°, pak vlastní funkce ψ°(x) musí být nula. Současně ale vlastní funkce nesmí být identicky nula (byl by to pak nulový vektor), takže v x° musí mít tato funkce nenulovou hodnotu. Ale jakou? Vlastní funkce jsou normalizované (tedy integrál přes celý definiční obor je jedna) a pokud ji v x° definujeme jakoukoliv konečnou hodnotou, celkový integrál bude stále nula. Toto dilema nakonec šalamounsky vyřešila tzv. Diracova delta funkce δ(x), která je všude nula, pouze v x° má hodnotu nekonečno.

Monstrum, které nabývá hodnoty nekonečno, ale rozhodně není klasická funkce. Aby se její chování dalo nějak smysluplně popsat, bylo nutno zapřáhnout novou matematickou hračku: distribuce) (neboli zobecněné funkce). Posviťme si na ně.

V úvodu citovaném Matykání jsme viděli, že v prostoru funkcí se na integrál ze součinu f(x) a g(x), což je – až na nějaké to znaménko – velikost plochy pod funkcí f(x)*g(x), díváme jako na skalární součin

(f,g) = ∫f(x) * g(x)dx

Když si zafixujeme funkci f(x), získáme zobrazení F (zvané funkcionál)), které každou testovací funkci g(x) zobrazí na číslo (pro běžné vektory jsme podobný trik viděli zde)

F: g(x) --> ∫f(x) * g(x)dx
(Mimochodem, výše definovaný integrální operátor třetího typu vlastně spočívá v tom, že si jádro nasekáme na spoustu testovacích funkcí a jejich skalární součiny s f nám udávají výstupní hodnoty výstupní funkce – vstupní hodnoty jsou určeny polohou řezu.)

Funkcionál F, který je určen naší pevně zvolenou funkcí f, je tedy skříňka, kam hodíme funkci g a trpaslík nám vyhodí číslo určené pravou stranou předchozí rovnice. A tento funkcionál bude základem našeho zobecnění pojmu funkce.

Platí zde jistá analogie. V klasické středoškolské matematice je funkce f něco, co provádí určitou akci na číslech (např. je umocňuje na druhou nebo počítá jejich sinus). Zobecněné funkce F jsou určeny svou akcí ne na číslech, ale na jiných (tzv. testovacích) funkcích, zde označených g.

Jinými slovy, na zobecněné funkce se nedíváme jako na skříňku, kam se hází čísla, ale jako na skříňku, kam se hází funkce. Trpaslík nám v obou případech vyhodí na výstup nějaké číslo v závislosti na tom, co jsme hodili dovnitř (ať už je to nezávisle proměnná x anebo testovací funkce g). A pomocí toho výstupu si naši funkci f/F pečlivě osaháváme.

To není tak absurdní náhled, jak by se na první pohled mohlo zdát. Vzhledem k tomu, že funkcionál F je de facto skalárním součinem, můžeme si ho představit jako velikost projekce funkce f do testovacích funkcí g (pro vektory to tak funguje). Pokud máme nějaký neznámý vektor, jedna z možností, jak o něm získat přesnější informace, je spočítat velikost jeho projekce do různých testovacích směrů. A přesně to zobecněné funkce dělají.

Distribuce jsou tedy funkcionály operující na přesně definovaném prostoru testovacích funkcí (obvykle hladké funkce, které jsou nenulové pouze na konečném intervalu). Pro každou „normální“ funkci f si takový funkcionál F vytvoříme výše uvedeným způsobem. Pointa distribucí spočívá v tom, že tyto funkcionály můžeme definovat i pro objekty, které nejsou „normálními“ funkcemi (byť v tom případě nemusí být nutně definované integrálem).

Např. zmíněná Diracova „funkce“ odpovídá funkcionálu

D: g(x) --> g(0)
(Pro každou testovací funkci g nám trpaslík vyhodí na výstupu číslo g(0); pokud rádi přemýšlíte, zkuste si takový funkcionál interpretovat jako skalární součin testovací funkce g a Diracovy „funkce“ δ, která má v nule hodnotu nekonečno a jinak je nulová.)

Takto definovaný funkcionál odpovídá funkci δ(x), jejíž „hmota“ je „soustředěná“ v nule a jejímž posunováním δ(x - x0) pak získáme vlastní funkce kvantového operátoru polohy. Laicky si ji můžete představit jako limitu stále užších a stále vyšších „hrbolků“ soustředěných kolem bodu x0.

Operátor hybnosti je definován vztahem

P: ψ(x) --> -iħ dψ/dx

(kde ħ je normalizovaná Planckova konstanta; mimochodem, ta derivace vpravo je technicky parciální, protože vlnové funkce závisí také na čase, ale pro potřeby Matykání si s tím nebudeme komplikovat život)

Pokud si derivaci označíme tradiční čárkou, pak hledaná vlastní funkce (s vlastním číslem p) musí splňovat vztah

• iħ ψ'(x) = p ψ(x)

Hledáme tedy funkci, jejíž derivace je rovna přímo té funkci samotné (krát nějaká konstanta). Je všeobecně známo (viz klasický vtip), že funkce, která se rovná své vlastní derivaci, je exponenciála (dokázat to ale není úplně triviální). A když se s těmi konstantami správně zacvičí, vyjde nám vlastní funkce v této podobě

ψ(x) = C exp(ipx/ħ)

Stejně jako v předchozím případě, ani tuto funkci není úplně snadné normalizovat. Pokud si vzpomínáte, exponenciála s imaginárním argumentem v podstatě popisuje bod obíhající po kružnici. Zahrneme-li do rovnice i časovou složku, dostaneme šířící se sinusoidu, tedy objekt, který je „rozprostřen“ po celém prostoru (což je v ostrém kontrastu s operátorem polohy, jehož vlastní funkce jsou koncentrovány do bodu). Abychom je mohli nějak lokalizovat, musíme je vhodně nakombinovat do tzv. vlnového balíčku.

Vlnová funkce nám tedy supluje jak vektor polohy, tak vektor hybnosti (rychlosti). Je to skutečná nositelka informace o stavu kvantového systému. Manipulace s ní je ale mnohonásobně obtížnější.

Vidíte, že studovat kvantovou mechaniku není žádná legrace. Člověk musí nejen umět velmi náročnou matematiku, ale ještě tomu musí i fyzikálně rozumět. Poklona těm, kdo se vydali na tuto cestu. Bez nich bychom byli technologicky sto let pozadu.

Článek je redakčně upravenou verzí blogového příspěvku na serveru iDNES.cz. Publikováno s laskavým svolením autora. Další díly a původní texty jsou dostupné na blogu Jana Řeháčka.

Autor: Jan Řeháček