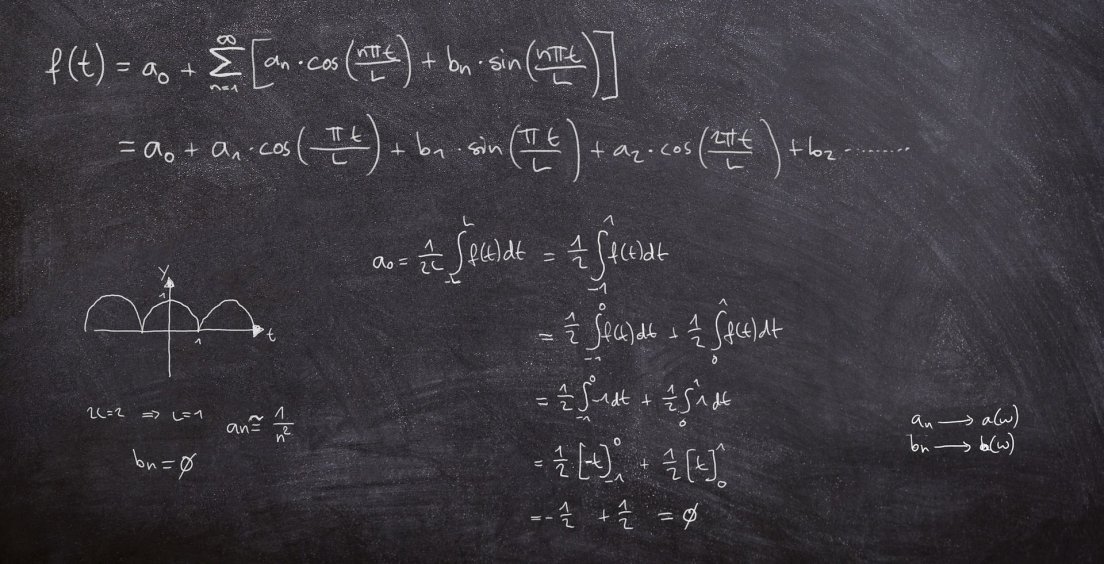Minule jsme viděli, že existují tři základní (a velmi odlišné) typy geometrií. Přirozená otázka tedy je, jakou geometrii má náš konkrétní 3D vesmír, ve kterém žijeme. Hledání odpovědi nás zavede k obecné teorii relativity.
(toto Matykání volně navazuje na epizodu o varietách)
První věc, která člověka napadne, když mu zlomyslní spolužáci prozradí, že gravitace je pouze důsledkem zakřivení vesmíru, je: „Hrome, jaké zakřivení? Cožpak je kosmos nějaké linoleum? Odkdy má náš milovaný vesmír extra dimenzi, ve které by se mohl zprohýbat?“
A skutečně, představa 3D prostoru, který se vlivem hmoty či hmotoenergie v něm plovoucí trochu „pokroutil“, přesahuje chápání běžného frekventanta základní školy (který měl nota bene zrovna chřipku, když se v šesté třídě probíraly Christoffelovy symboly).
Ale ono to není tak, že si pán Bůh pět minut před velkým třeskem usmyslel, že ten čerstvě upečený vesmír, který právě vytáhl ze šquarkové trouby, hezky pěkně ohne přes koleno, aby měli ti fiškulíni za 14 miliard let o čem přemýšlet. Světlo se, pravda, šíří po obecně křivočarých geodetikách, ale to neznamená, že se náš prostor vezdejší musí nutně křivit v nějakém vyšším hyperprostoru.
Zakřivení vesmíru (a obecně nějaké variety) se dá odvodit z jeho metrických vlastností, tedy zhruba řečeno ze způsobu, jakým v něm měříme vzdálenosti. I zcela „rovná“ plocha může mít křivočarou (ne-eukleidovskou) geometrii, zatímco plocha z našeho pohledu evidentně „křivá“ může mít běžnou rovinnou geometrii (tj. eukleidovskou). Tento zdánlivý paradox je způsoben tím, že slovo „křivost“ funguje v jazyce na dvou úrovních.
V kontextu, řekl bych, občanském toto slovo používáme ve smyslu zakřivení objektu určitým způsobem „vytvarovaného“ v nějakém vícerozměrném prostoru (např. zakřivená 2D sféra v našem 3D světě) a je odvozeno od intuitivního konceptu „ohnutosti“, respektive jeho opaku, tj. „rovnosti“. Tato křivost se na vlastnosti toho obklopujícího prostoru zhusta odvolává, a proto jí říkáme externí. Bytosti žijící uvnitř takto zakřiveného objektu (naši milí plošníci) by toto zakřivení ale vůbec nemuseli zjistit (alespoň ne lokálně). Jejich děti by se ve škole učily přesně tu samou geometrii, co my.
V matematice ale slovo „zakřivení“ obvykle znamená křivost interní (tedy tu Gaussovu), která je vůči ohýbání invariantní a která určuje kvalitativní typ geometrie v zakřiveném objektu panující, tedy vztahy mezi různými geometrickými veličinami. Například poměr mezi obvodem kružnice a jejím poloměrem je v eukleidovské geometrii přesně 2π, zatímco v hyperbolické je o něco více a ve sférické o něco méně.
Takové věci si plošníci v pohodě naměří sami, aniž byste je museli za flígr vytahovat z variety ven. Schválně si spočítejte, jaký je poměr mezi délkou rovníku (což je obvod sférické kružnice) a vzdáleností rovník – severní pól (což je její sférický poloměr – vzdálenost, kterou plošník urazí při cestě z kružnice na její střed). No vidíte, a hned víte, že Země není placatá. Ani nemusíte být kosmonautem nebo mořeplavcem.
Díky tomu by se plošníci žijící uvnitř 2D objektu (v našem případě zakřivené plochy) mohli charakteru jeho „zakřivení“ dopídit pouhým proměřováním geometrických vlastností trojúhelníků, kružnic, kosočtverců a dalších nemravných útvarů. Aniž by svou plochu opustili a podívali se na ni zvnějšku, aniž by ve svých výpočtech použili naše 3D souřadnice, zjistili by, že žijí na sféře (či přesněji na ploše, kde platí zákony sférické geometrie).
Vesmír tedy nepotřebuje žádné další dimenze, ve kterých by se mohl křivit. Charakter jeho geometrie se dá zjistit čistě studiem objektů v rámci jeho vlastního 3D prostoru (či přesněji 4D časoprostoru) a není potřeba si lámat hlavu s tím, zda prostor sám o sobě ještě náhodou neplave v nějakém vícedimenzionálním médiu. Z pohledu jeho zakřivení (a pokud neřeknu jinak, mám na mysli to interní) je to totiž úplně fuk.
Pokud vám to nepřipadne dostatečně matoucí, zkusím to říci takto: i zdánlivě zakřivený prostor může mít eukleidovskou geometrii, takže plošníci v něm žijící naměří svým trojúhelníkům na vnitřních úhlech přesně 180°. A naopak, i do prostoru rovného jak prkno můžeme s úspěchem importovat libovolnou křivočarou geometrii (ať sférickou či hyperbolickou), takže jeho plošníci naměří v trojúhelnících určité úhlové odchylky (ve sférické jim součet vyjde „nad“ 180°, v hyperbolické „pod“). Stačí vhodně změnit způsob, jak v něm „měříme“ vzdálenosti.
Vezměme si milimetrový papír (který v životním prostoru plošníků představuje soustavu souřadnic) a nenápadně ho ohneme. Protože při tom ohnutí se rozměry čtverečků nijak nezmění, plošníci žijící v našem papíru nebudou mít nejmenšího šajna, že se něco změnilo. Všechny vzdálenosti, které naměřili před ohnutím, budou stejné jako po ohnutí a ani úhly se nezmění (jejich měření je lokální a probíhá de facto v tečné rovině). Pokud papír nesrolujeme do válce (čímž bychom jim dali možnost ho „obeplout“), tak nikdy nezjistí, že nežijí v eukleidovské rovině.
Teď si možná říkáte: no dobře, tak ten ohnutý papír prostě ohneme ještě jednou (podél jeho „hřbetu“), takže bude mít kladnou Gaussovu křivost (v obou hlavních směrech se bude křivit kladně), a tím pádem nabude sférickou geometrii. Plošníkům nic neřekneme a podobnou úvahou bychom pak mohli argumentovat, že ani v tomto případě nebudou mít šanci se o sférickém charakteru svého světa dozvědět. Chyba lávky! Jen si to s tím papírem schválně zkuste.
První zakřivení bude v pohodě. Papír se ohne raz dva. Když ho ale vezmete a budete se ho snažit ohnout „podél hřbetu“, zjistíte, že milá buničina se najednou vzpouzí a nechce se nechat ohnout. Začne se vám krabatět, popřípadě trhat. Eukleidovský charakter papíru nechce a nechce přijmout zákony sférické geometrie, které by v něm po dvojím ohnutí začaly platit. Jediná šance, jak na to vyzrát, je vzít si milimetrový papír z gumy (či jiného lehce roztažitelného materiálu) a pak ho můžeme jemně zakřivit i podél hřbetu. Budeme ho ale při dvojím ohýbání muset stále dotvarovávat, aby získal kýžené kulovité zakřivení.
Během tohoto procesu zjistíme šokující věc. Jak jsme ten náš gumový milimetrák hnětli zhruba do tvaru kulového vrchlíku, tak se nám ty milimetrové čtverečky tady trochu natáhnuly, zatímco onde se nám zase pro změnu trochu smrskly. Takže jejich strany už neměří všude 1 mm, ale tady 1.1 mm a onde zase 0.9 mm. Jednotkový nárůst té či oné souřadnice bude mít tedy na reálnou vzdálenost trochu jiný dopad než před hnětením.
A přesně v tom je skryto jádro pudla. Z pohledu plošníků se charakter geometrie daného prostoru odvíjí od jeho metrických vlastností, tedy od výsledků měření vzdálenosti prostřednictvím souřadnic. A na to si dnes posvítíme.
Metrika teoreticky
Měření vzdáleností na zakřivené ploše (varietě)) je v podstatě měřením délky křivek po ní se plazících. Nic jiného v podstatě nedává smysl. Vzdálenost Praha – New York je prostě délka nejkratší křivky (geodetiky) tyto body spojující. Kdybychom tu vzdálenost chtěli počítat eukleidovsky (z 3D prostoru, do kterého je naše 2D sféra vnořená), tak bychom museli mezi Prahou a New Yorkem vykopat tunel.
Podívejme se proto trochu podrobněji na to, jak měří vzdálenosti naši plošníci, žijící na milimetrovém papíru (a ruku na srdce, na milimetrovém papíru by chtěl žít každý).
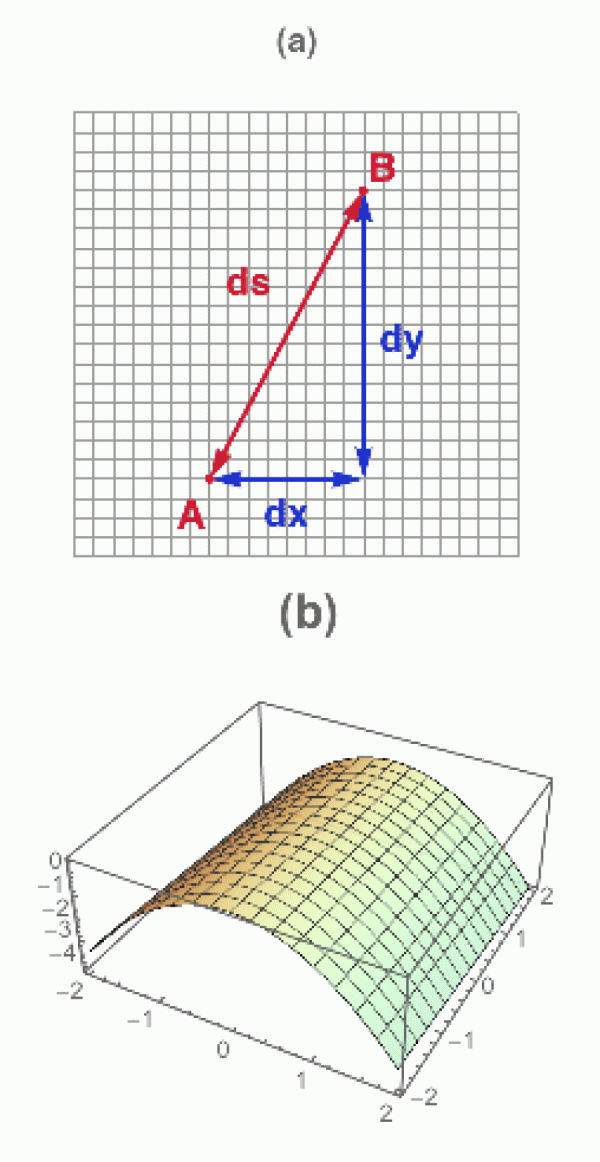
Nejprve v hrubém náčrtu (obrázek a).
Čtverečky milimetrového papíru nám poskytnou souřadnice, ze kterých vzdálenosti odvodíme. Postavíme se do bodu A = (x, y) a abychom se dostali do bodu B, musíme udělat dx = 8 kroků ve směru vodorovném (osa x), dy = 15 kroků ve směru svislém (osa y). Tolikrát jsme tedy přelezli souřadnicové linie při cestě z A do B.
Podle Pythagorovy věty bude celková vzdálenost ds mezi bodem A a B (tj. délka křivky tyto body spojující) rovna
ds2 = dx2 + dy2
Spočítal jsem rovnou její čtverec, říkáme mu délkový element, abychom se nemuseli stále tahat s odmocninou.
(Těmi déčky se nenechte zmást: „dx“ je stále jen jedna veličina – v učebnicích samozřejmě reprezentuje diferenciál), tedy infinitesimální změnu x, ale pro potřeby Matykání bude stačit, když se na tuto veličinu nebudeme dívat jako na „nekonečně malou“, ale jako na „dostatečně malou“ změnu, aby se pro potřeby daného výpočtu daly ostatní veličiny považovat zhruba za konstantní – dx bude tedy znamenat zhruba to, co se v učebnicích většinou označuje typograficky obtížnějším symbolem Δx)
V našem případě tedy bude červená délka křivky (vzdálenost AB) rovna
ds = 17
Při ohnutí papíru (obrázek b) se na způsobu výpočtu vůbec nic nezmění. Změna tvaru vzdálenosti nemění. Provázek délky 10 cm bude stále stejně dlouhý i ve stavu stočeném do spirály. Pokud plošníci na ohnutém papíru přelezou 8 čtverečků, bude to stále odpovídat 8 délkovým jednotkám. Délkový element je beze změny.
Teď ale někdo ten náš krásný gumový milimetrový papír vezme a ve snaze vytvarovat z něho sféru (nebo alespoň kulový vrchlík) ho začne různě natahovat, takže plošník přeskočivší 4 čtverečky urazí ve skutečnosti o něco větší vzdálenost. Natahování vzdálenosti mění. Pokud bude náš provázek z gumy, po natáhnutí může klidně měřit 15 cm.
Předpokládejme, že roztahování proběhlo v okolí bodu A podél souřadnicových směrů. Řekněme, že ve směru x jsme gumový papír roztáhli o faktor a, zatímco ve směru y o faktor b. Těmito faktory tedy musíme pronásobit „počty překročených čtverečků“, abychom dostali kýženou vzdálenost (resp. její čtverec):
ds2 = a2dx2 + b2dy2
A protože gumový papír můžeme roztahovat i podél ostatních směrů (ne nutně podél souřadných os), v obecném případě nám v tomto vzorečku vyskočí i člen dx.dy (zhruba ze "stejného důvodu":2, z jakého vám takový člen vyskočí při počítání rovnice elipsy, jejíž osy se liší od os souřadných).
Takže plošníci, s jejichž gumovou plochou jsme právě zle zacvičili, naměří obecně:
(+) ds2 = g(1,1) dx2 + g(1,2) dx.dy + g(2,1) dy.dx + g(2,2) dy2
(kde všechna ta géčka jsou prostě koeficientíky – jako byly v předchozí formulce a či b – vyjadřující roztažení naší gumové plochy)
Pokud budete potřebovat zjistit např. délku nějaké křivky, prostě tu křivku rozdělíte na několik malinkatých kousíčků (abyste mohli předpokládat, že uvnitř těch malých kousíčků se roztahovací koeficienty moc nemění), pro každý kousíček spočítáte délku podle formulky (+) výše (podle toho, kolik jste přelezli čtverečků) a nakonec to všechno posčítáte.
V té formulce (+) jsem členy dx.dy a dy.dx nesdružil, abych ji mohl zapsat maticově
(++) ds2 = (G.u,u)
Zde u je vektor souřadných rozdílů (dx, dy), G je matice složená z géček, tj. z lokálních „roztahovacích“ či „smrskávacích“ koeficientíků a závorka naznačuje další skalární součin.
Koeficienty g(i, j) se pochopitelně při pohybu po ploše trochu mění (protože někde ji roztahujeme více, jinde méně), takže tu matici G si představte jako funkci souřadnic. No a máme zhruba definován metrický tenzor – ani to moc nebolelo.
Tenzory jsou obecně vzato velmi komplikované veličiny, ale můžete si je zhruba představit jako funkce s několika vektorovými vstupy, které na výstupu vždy vyhazují skalár. Funkce jsou lineární ve všech proměnných, a proto fungují na bázi skalárního součinu. Počtu vstupů říkáme řád tenzoru. Např. matice G je tenzor druhého řádu, protože abychom z ní vydyndali číslo, musíme ji nejprve skalárně pronásobit nějakým vstupním vektorem u: G.u a takto vzniklý vektor pak pronásobit dalším vstupním vektorem v, což už nám dá skalár: (G.u,v). Proto si spousta lidí tenzory představuje prostě jako matice (přestože pojem tenzoru je podstatně obecnější). Předchozí vzoreček (++) je trochu speciální v tom, že jsme do tenzoru G vhodili na oba vstupy ten samý vektor u. Vektory samy o sobě jsou tenzory 1. řádu, protože reprezentují lineární funkci s jedním vstupem: zafixujeme si vektor v, na vstup funkce (tímto vektorem určenou) vhodíme vektor u a na výstupu nám rázem vypadne číslo (v, u) či v.u (podle toho jak značíte skalární součin). V plné obecnosti je celá záležitost bohužel o něco komplikovanější, protože do některých vstupů házíme vektory a do jiných kovektory, takže při definici řádu tenzoru to musíme rozlišovat, ale s tím si nebudeme kazit jaro.
A teď o něco abstraktněji.
Před časem jsme si řekli, že základem měření ve vektorových prostorech je skalární součin, ze kterého lze odvodit jak úhel mezi dvěma vektory, tak normu vektoru (která udává jeho velikost čili délku).
A protože v každém bodě p nějaké hladce zakřivené plochy M můžeme zkonstruovat tečný prostor (což je nejlepší eukleidovská aproximace v tom bodě), můžeme zkoumání vzdáleností na ploše lokálně přesunout do příslušného tečného (vektorového) prostoru, kde máme připraven bohatý aparát lineární algebry.
Postavíme se tedy do bodu p naší plochy M (obecněji variety) a tečný prostor si označíme T – ten se samozřejmě bod od bodu mění, takže ho v učebnicích často uvidíte se subscriptem p (TpM). V tomto tečném prostoru máme definován skalární součin vektorů u a v, pro který si geometři vymysleli další symbol: g(u,v). Nemusí to být nutně ten středoškolský, ale musí splňovat obvyklá pravidla. A protože i ten součin se může v principu měnit bod od bodu – každý tečný prostor může mít ten skalární součin definován trochu jinak – i zde se často setkáte se subscriptem p.
(Mystické g(u, v) je tedy stejný typ zvířátka jako u.v nebo (u, v), jen se může bod od bodu měnit – a pokud uvidíte skalární součin značen tímto způsobem, obvykle to znamená, že se nacházíte v kontextu Riemannovy geometrie, kde se funkci g, která skalární součin zprostředkovává, říká metrický tenzor nebo též první fundamentální forma.)
Takže stojíme v bodě p, kolem sebe vidíme varietu M s tečným prostorem TpM a jeho jednotkové bázové vektory si označíme u a v. Nakombinujeme si z nich vektor w a vyrazíme po varietě v tomto směru. Po určité době bude naše přemístění reprezentováno malým vektorem
dw = (du,dv) = du u + dv v
Udělali jsme tedy malý krůček du (ve směru u), malý krůček dv (ve směru v) a délku ds takto zkonstruovaného vektoru dw spočítáme skalárním součinem (a abych se nemusel tahat s odmocninami, budu opět používat délkový element):
ds2 = ‖dw‖2 = g(dw,dw) = g(du.U + dv.V, du.U + dv.V)
Z linearity (a komutativity skalárního součinu g) pak obdržíme „roznásobením“
ds2 = g(U,U) du2 + 2 g(U,V) du dv + g(V,V) dv2
nebo pomocí složek vektoru dw
(+++) ds2 = (G.dw, dw)
což je formálně stejný tvar jako (++), jen v tomto případě dostaneme koeficienty !roztahovací" matice G pomocí riemannovských skalárních součinů g(1, 1) = g(U, U), g(1, 2) = g(U, V), atd.
Pokud budete číst nějaký text o obecné relativitě, musíte vzít navíc v úvahu, že v „rovném“ časoprostoru neměříme délku vektorů eukleidovsky, tj. součtem čtverců, ale lorentzovsky: ‖(dx,dy,dz,dt)‖ 2 = dx2 + dy2 + dz2 - dt2. Obdobně je nutno upravit skalární součin. Časoprostor je tedy varieta, která se lokálně podobá ne eukleidovskému, ale lorentzovskému prostoru (Minkowského prostor). Metrický tenzor se na ní ovšem definuje obdobným způsobem), tedy v každém bodě p je to funkce, která zprostředkovává lorentzovský skalární součin na příslušném tečném prostoru. Takto vzniklým zakřiveným varietám pak říkáme Lorentzovy variety, či obecněji pseudo-Riemannovy.
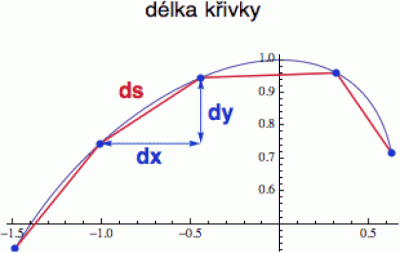
Ať se na to díváte tak či onak, v obou případech je na konci formulka, která nám říká, jak spočítat délkový element ds2 (tedy čtverec délky kousíčku nějaké křivky) ze změn lokálních souřadnic. Po odmocnění pak z lokálních délek ds spočítáme celkovou délku libovolné křivky integrací (tedy spojitou variantou součtu). Pokud máte na integrál alergii, můžete si ji představit jako prostý součet několika „dostatečně malých“ délek ds (jak je naznačeno na obrázku), s tím že pak dostanete pouze přibližnou hodnotu délky, protože úsečkové spojnice ke křivce úplně přesně nepřiléhají (to by se nám podařilo pouze v infinitesimálním případě).
Ve vícerozměrném případě se souřadnice obvykle číslují (x1, x2 atd.), ale délkový element se stále definuje pomocí metrického tenzoru
(*) ds2 = Σ Σ g(i, j) dxi dxj
kde g(i, j) jsou jeho složky, dxi je malý nárůst i-té souřadnice a sumace běží přes všechny indexy i, j - tak jak by odpovídalo maticovému zápisu ds2 = (G.du,du). Ve fyzice dokonce sumační symboly často ani neuvidíte, protože se používá Einsteinova konvence, která většinu komplikovaných vzorečků trochu zpřehlední (tím, že vyhází implicitně definované sumační symboly).
Formulka (*) je pro diferenciální geometrii – a jakoukoliv disciplínu zabývající se zakřivenými prostory – naprosto kruciální. Z měření délek podél křivek vyplývá většina našich metrických znalostí o varietě, ve které žijeme (v našem případě je to 4D zakřivený časoprostor, v případě plošníků 2D zakřivená plocha), a z těchto znalostí pak můžeme odvodit typ geometrie, který v dané varietě panuje, aniž bychom museli tu varietu opustit (respektive přesunout se do nějaké vyšší dimenze, ze kterého bychom si její zakřivení mohli prohlédnout). A je v podstatě jedno, zda se na ta géčka díváte jako na jakési lokální roztahovací koeficienty anebo jako na koeficienty popisující chování skalárního součinu.
Důležité je, že práce s délkovým elementem je lokální. Jakmile se na varietě kousek posuneme, dostanete trochu jiný tečný prostor, který může mít v principu trochu jinou definici skalárního součinu (či jiné lokální roztažení gumové plochy). Proto je nutno při sumačních výpočtech používat buď calculus, anebo velmi opatrně sledovat, jak moc se během našeho výpočtu ostatní veličiny mění, a tomu přizpůsobit příslušné aproximace.
V příští sekci si ukážeme, jak se derivacím a integrálům elegantně vyhnout.
Metrika prakticky
Z pozice geometrických božstev si nejprve stvoříme úplně obyčejnou eukleidovskou rovinu, což se většinou provede hromovým zaburácením „Budiž rovina!“ (popřípadě, pokud dojde k nedostatkům v zásobování milimetrovým papírem, zlověstným zamrmláním "Dexempo Multo Federex“). Ale než do tohoto 2D vesmíru vypustíme naše „plošníky“, pošeptáme jim do ouška, že vzdálenosti se v jejich novém výběhu měří podle vzorečku:
(**) ds2 = (dx2 + dy2) / y2
(tj. složky metrického tenzoru jsou g(1,1) = 1/y2, g(2,2) =
1/y2, g(1,2) = g(2,1) = 0)
Po odmocnění se na to můžeme dívat tak, že to, co plošníci naměří, bude obvyklý eukleidovský element de vydělený y.
(***) ds = de / y
Toho nejchytřejšího plošníka postavíme do bodu A = (1, 2) a necháme ho spočítat vzdálenost k bodu B = (1.2, 2.1). Chytroplošník brzy zjistí, že rozdíl souřadnic mezi bodem A a B činí dx = 0.2 a dy = 0.1. Pokud by plošníci měřili vzdálenosti eukleidovsky, napočítali by de2 = 0.22 + 0.12 = 0.05, takže de = 0.2236 (což je vzdálenost mezi body A a B dle našich školních osnov).
Plošníci se ovšem neřídí našimi školními osnovami, ale pokyny svého Boha, a proto musí ještě ten součet čtverců vydělit. Otázka je, zda ho máme vydělit y-souřadnicí bodu A, anebo B.
Protože jsme se rozhodli upustit od infinitesimálních přírůstků a spokojit se s přibližnými hodnotami, vybereme si prostě bod, jehož y-souřadnicí se nám bude lépe dělit, tedy A (pro bod B bychom dostali číslo trochu jiné, byť velmi podobné)
ds = de / 2 = 0.1118
a za tuto vzdálenost bodů A a B by náš chytroplošník dostal od pana učitele jedna mínus. Jedničku by dostal, pokud by vzdálenost mezi A a B rozsekal na pár menších kousíčků a mezivýsledky sečetl (jak si ukážeme v příští sekci), pak by ta chybka ze zanedbání calculu byla ještě menší. No a jedničku s hvězdičkou by dostal za integraci (tedy spojitý součet infinitesimálních kousíčků). Pokud by totiž každý z těch kousíčků měl stejnou y-souřadnici, tak bychom toto dilema vůbec nemuseli řešit.
Z toho jednoduchého vzorečku (***) mimochodem vyplývá, že pokud jsou plošníci daleko od osy x (y je v absolutní hodnotě velké číslo), jejich naměřené vzdálenosti budou podstatně menší než ty, které bychom ze stejných souřadnicových rozdílů napočítali my. Jak se ovšem přibližují k ose x, jejich spočítané vzdálenosti se zvětšují a v bezprostřední blízkosti osy x se dokonce limitně blíží k nekonečnu. Z pohledu plošníků je tedy osa x daleko, předaleko (proto se také u tohoto modelu geometrie uvažuje pouze horní polorovina, jak uvidíme příště).
Je to trochu divný vesmír, takže si jeho zákony chvilku rozmyslete.
Teď když víme, jak plošníci ve světě, který jsme jim stvořili, počítají malé (téměř infinitesimální) vzdálenosti, pojďme se podívat, jak si z nich sesumírují délku křivky (aby se to nepletlo, tak eukleidovské délky budu značit d, plošnické d').
Vezmeme si bod A = (1,1) a přesuneme se do bodu B = (-1, 1) podél dvou různých křivek. Jednak podél modré kružnice K se středem v počátku a poloměrem r = sqrt(2) a jednak podél naznačené červené přímky P.
Abychom se nemuseli lopotit s integrály, rozdělíme si obě křivky na malé (byť ne zcela infinitesimální) kousky, spočítáme přibližnou plošnickou délku d' každého kousku, tak jako jsme to udělali výše, a nakonec je všechny sečteme. Konkrétně obě křivky rozsekáme na 10 menších kousků (viz obrázek).
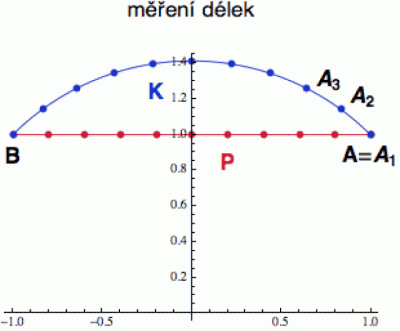
Pro kontrolu: body na modré kružnici jsou
A = A1 = (1, 1)
A2 = (0.831, 1.144)
A3 = (0.642, 1.260)
...
B = A11 = (-1, 1)
Tyto body už jsou dostatečně blízko, takže nás nemusí trápit, že hodnota y (kterou budeme příslušné vzdálenosti vždy dělit) se trochu mění. V souladu s předchozím příkladem budeme každou dílčí eukleidovskou vzdálenost (a ty jsou v tomto případě stejné) dělit y-souřadnicí prvního bodu (pro přesnější výpočet si zkuste dělit průměrem y-souřadnic prvního a druhého bodu).
Plošnická vzdálenost mezi body A1 a A2 bude:
ds = de / y = 0.221916 / 1 = 0.221916
mezi body A2 a A3:
ds = de / y = 0.221916 / 1.144 = 0.193962
Podobně spočítáme i ostatní vzdálenosti (nejlépe programovatelným počítačem) a zjistíme, že součet oněch deseti hodnot ds nám dá přibližnou plošnickou délku křivky K
d'(K) ~ 0.222 + 0.194 + 0.176 + 0.165 + 0.159 + 0.157 + 0.159 + 0.165 + 0.176 + 0.194 = 1.7667
Z našeho eukleidovského pohledu by samozřejmě byla jiná: protože je to přesně čtvrtkruh o poloměru sqrt(2), nemusíme nic sčítat ani integrovat a dostaneme hned ze známého vzorečku: d(K) = 2π r/4 = 2.22144.
A teď se podíváme na to, jaká je délka modré přímky. Podél ní se y vůbec nemění, takže nemusíme nic sekat na drobno, protože v každém bodě bude „plošnická“ délka ds prostě konstantním násobkem délky eukleidovské de. Celková délka bude tedy eukleidovská délka úsečky AB vydělená y = 1, což nám dá d'(P) = 2. Pokud se vám to nezdá, klidně si úsečku nasekejte na 10 dílečků, abyste na vlastní oči viděli, jak se to „společné“ y dá z celého výpočtu vytknout. Eukleidovská délka této přímky je, díky konstantní hodnotě y = 1, stejná: d(P) = 2.
Zjistili jsme tedy zajímavou věc. Z pohledu plošníků bude modrá kružnice kratší spojnicí bodů A a B než červená přímka: d'(K) = 1.76 < 2.0 = d'(P). Už to ukazuje, že ve světě těchto plošníků nebude vládnout eukleidovská geometrie, protože v ní by nejkratší spojnicí bodů A a B musela být červená přímka – což pro nás Eukleiďany skutečně platí: d(P) = 2.0 < 2.22 = d(K).
Zatím samozřejmě není jasné, jaká geometrie v tomto světě vládne. Modrá kružnice nemusí být nutně nejkratší spojnicí obou bodů. Možná existuje ještě nějaká kratší. To nás pro tuto chvíli bolet nebude – časem uvidíme, že modrá kružnice je skutečně nejkratší křivkou mezi oběma body (a že geometrie, která takto vznikne, bude hyperbolická).
Pro tuto chvíli se pouze spokojíme se zjištěním, že jsme plošníkům jejich svět nijak nezohýbali. Pouze jsme změnili definici toho, jak se v něm měří vzdálenosti. A přesto v takovém vesmíru, který je stále nominálně rovný jako prkno, už evidentně neplatí eukleidovská geometrie.
Pokud rádi používáte selský rozum, můžete na celou situaci pohlížet takto: chcete postavit železnici z bodu A do bodu B, ale protože podél osy x teče důležitá řeka, pozemky, na kterých budete stavět, mají tím vyšší cenu, čím jsou blíže řece (cena pozemku zde tedy supluje „plošnickou“ délku). Jste-li dvakrát dále od řeky, cena pozemku bude dvakrát menší. Každý businessman vám řekne, že se musí začít stavět směrem na severozápad, kde je půda lacinější, a teprve když ve směru západním urazíme určitou vzdálenost, budeme se muset začít stáčet k jihu (byť jsou tam pozemky dražší), protože výsledně musíme dorazit do bodu B. Takové je zadání projektu. A když si tuto úlohu zoptimalizujete, vyjde vám červená kružnice jako nejlacinější řešení. A ze stejného důvodu se plošníkům (jak uvidíme časem) bude jevit jako nejkratší spojnice mezi oběma body.
Pokud rádi integrujete, můžete si místo toho přibližného „běžného“ součtu lajsnout součet spojitý, tedy integrál, v němž budeme sčítat skutečné infinitesimální veličiny:
d'(K) = ∫ ds = ∫ de/y = ∫ √(dx2 + dy2) / y
zde ty infinitesimální změny dx, dy dostaneme z parametrických rovnic kružnice
x = cos(t) a y = sin(t)
pomocí derivací
dx/dt = -sin(t) a dy/dt = cos(t)
které nám umožní je převést na infinitesimál parametru: dt
dx = -sin(t)dt a dy = cos(t)dt
takže po dosazení dostaneme
d'(K) = ∫ dt / sin(t) = 1.76275
(odkud kam máme integrovat nám prozradí parametr t: od π/4 do 3π/4)
Vidíte, že i bez znalosti integrálního počtu jsme nahoře prostým sčítáním dostali poměrně solidní odhad přesné hodnoty d'(K). Jen jsme místo spojitého součtu infinitesimálních přírůstků ds provedli normální součet rozumně malých přírůstků ds (mezi těmi modrými body).
Teď už trochu vidíte, jak interní a externí křivost funguje.
Minule jsme plošníky vysadili na válec (který se nám externě jeví jako zakřivený) a zjistili jsme, že v něm stále platí eukleidovská geometrie. Tedy za předpokladu, že jsme ho během ohýbání nikterak nezdeformovali - tj. že se vzdálenosti na tom milimetrovém papíře nijak nezměnily. Dnes jsme je naopak vysadili do roviny (která se nám externě jeví naprosto "placatá") a pouhou změnou metrického tenzoru (tj. způsobu měření délek) jsme docílili toho, že z pohledu plošníků se její geometrie chová jako křivočará (byť ani chytroplošník zatím netuší, zda bude sférická či hyperbolická). Jejich „vesmír“ má tedy určitou interní křivost. Plošník Vančura by to mohl shrnout takto: „Tento způsob světa zdá se mi poněkud neeukleidovským.“
Tohle odpoutání se od vnějších projevů zakřivení a koncentrace na vnitřní proměřování, které si plošníci mohou sami provést uvnitř dané variety, je poměrně obtížný konceptuální krok, se kterým je potřeba se vyrovnat, pokud chce člověk nějak uchopit to, jak se náš vesmír vlastně „křiví“.
Mimochodem, například v komplexní rovině, která je plochá jak dvě prkna (jedno reálné a jedno imaginární), si samozřejmě můžete vytvořit model eukleidovské roviny tím, že ztotožníte každé komplexní číslo z = x + iy s bodem Z = (x, y) a pak budete provádět běžná měření podle Pythagorovy věty (a komplexní čísla můžete skutečně využít jako nástroj pro výuku eukleidovské geometrie).
V té samé komplexní rovině si ale můžete vytvořit model jak pro sférickou, tak pro hyperbolickou geometrii vhodnou změnou metriky.
Pro sférickou budete vzdálenosti měřit takto:
ds2 = (dx2 + dy2) / (1 + x2 + y2)
zatímco hyperbolický model si vytvoříte takto:
ds2 = (dx2 + dy2) / (1 - x2 - y2)
Všimněte si, že v obou případech máte ve jmenovateli výraz obsahující čtverec absolutní hodnoty komplexního čísla x + iy s tím, že ve sférickém případě ho přičtete k jedničce, zatímco v hyperbolickém ho od jedničky odečtete – proto je také tento model nutno provozovat pouze uvnitř jednotkového kruhu, abychom nedělili nulou (k tomu se časem dostaneme podrobněji).
Pokud rádi programujete, můžete si zkusmo spočítat (tak jako jsme to udělali nahoře) délku různých křivek mezi danými body podle eukleidovské, sférické či hyperbolické metriky a porovnat je s délkami přímek.
Zatím jsme vesměs zápasili se souřadnicemi kartézskými (které známe ze školy). Na zakřivených varietách se ale často používají speciální typy souřadnic, které reflektují jejich geometrický charakter. Např. na rotačním hyperboloidu bychom k jejich definici mohli použít hyperbolické funkce. Na sféře se zase s úspěchem používají o něco známější sférické souřadnice, které v běžném životě označujeme jako zeměpisnou šířku θ (rovnoběžky) a délku φ (poledníky). Jen pozor, v matematice obvykle šířku počítáme od severního pólu (θ = 0) směrem dolů, nikoliv od rovníku na obě strany.
Asi jste zaregistrovali, že pokud stojíte na rovníku (θ = 90), pak jednotková změna zeměpisné délky φ způsobí podstatně větší změnu vzdálenosti, než když stojíte třeba na polárním kruhu (θ = 23°66′). Metrický tenzor ve sférických souřadnicích proto musí tuto skutečnost nějak reflektovat (nemůžeme prostě posčítat čtverce změn souřadnic dr2 + dθ2 + dφ2 jako v kartézském případě). Člen odpovídající nárůstu zeměpisné délky dφ musíme pronásobit koeficientem, který závisí na zeměpisné šířce θ. Konkrétně takto (odvození zde):
ds2 = dr2 + r2 dθ2 + r2 sin(θ) 2 dφ2
(na jednotkové sféře, r = 1 a dr = 0, se tento výraz ještě zjednodušší)
Rozumný člověk si teď pomyslí, proč prostě nepoužíváme pouze kartézské souřadnice. Ty se sice dají definovat lokálně v okolí každého bodu, kde v podstatě představují kartézské souřadnice přenesené z příslušného tečného prostoru (říkáme jim normální souřadnice), ale ty se bohužel nedají globálně „protáhnout“.
Představte si třeba velký plážový míč, ke kterému jako improvizovanou tečnou rovinu přiložíte drátěné síto. Stíny drátů vám v okolí bodu dotyku vytvoří na míči krásný kartézský souřadnicový systém (to je v podstatě myšlenka „exponenciálního zobrazení“, které jsme už jednou viděli). Když se tuto kartézskou soustavu ale budete snažit rozšířit a budete se pokoušet míč tím drátěným sítem globálně obalit, tak se vám najednou dráty počnou ohýbat, síto začne krabatět a prostě to nepůjde. No bodejť by to šlo. To síto má eukleidovskou geometrii, zatímco míč má sférickou. Na pravou nohu levou botu nenasadíš.
Přesto by bylo užitečné, kdyby bylo možné lokální kartézské soustavy (z prosvíceného tečného síta) alespoň nějakým způsobem vzájemně porovnávat. Aby si plošníci žijící v různých oblastech variety mohli vyměňovat zkušenosti ohledně charakteru lokální geometrie na jejich dvorečku. To ovšem souvisí s „přirozenou identifikací“ tečných prostorů a tím se dostáváme zpátky k paralelnímu přenosu vektorů.
Sekce Jauvajs: Paralelní přenos II
(pouze pro mimořádně otrlé povahy)
Podívejme se nejprve, proč s tím paralelním přenosem děláme takové cavyky.
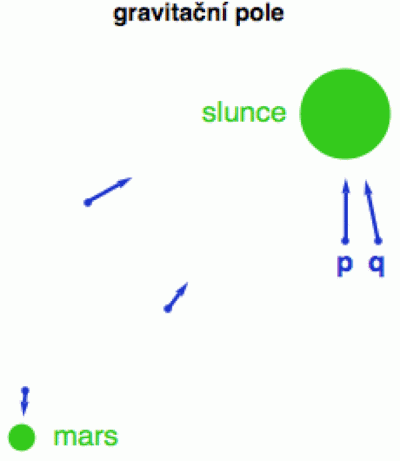
Spousta zajímavých veličin se v matematice dá vyjádřit pomocí vektorových polí. V eukleidovském prostoru si například můžete představit silové pole (řekněme gravitační), což znamená, že v každém bodě p definujete modrý vektor, který ukazuje, jaká síla bude v tomto bodě na nějaký hmotný objekt působit. A protože ta síla není konstantní, ale mění se bod od bodu, vyjadřujeme ji pomocí speciální funkce, které říkáme „vektorové pole“. Můžete si ji představit jako bedničku, do které na vstupu vhodíte polohový vektor bodu p (ukazující, kde se zrovna nalézáte) a na výstupu vám vypadne modrý vektůrek v, vyjadřující v jakém směru silové pole působí (viz schematický obrázek). V případě 3D prostoru se tedy jedná o funkci
v = V(p), kde V: R3 --> R3
Vektorové pole ale může fungovat i na zakřivené varietě M, např. na povrchu zeměkoule. Každému bodu p můžeme přiřadit třeba momentální směr větru, což bude náš vektor v (hezkou animaci, jak takové vektorové pole vypadá pro různé časy, najdete zde). V tomto případě je vektorové pole funkcí, kde na vstupu vhazujeme souřadnice bodu p variety M (třeba zeměpisnou šířku a délku) a na výstupu dostaneme vektor z jejího tečného prostoru TpM (směr větru).
V = V(p), kde V: M --> TpM
(eukleidovský prostor je sám sobě tečným prostorem, takže tam to nemusíme
rozlišovat)
V obou případech nás zajímá, jakým způsobem se vektorové pole mění. Tedy jak se změní vektor působící síly (či směr větru), pokud se přesuneme z bodu p do bodu q (viz předchozí obrázek). Změna bude pochopitelně závislá nejen na příslušném vektorovém poli, ale i na směru, ve kterém pochodujeme, např. pokud máme namířeno do závětří, bude vektorové pole slábnout, zatímco ve směru opačném bude pravděpodobně sílit.
V eukleidovském prostoru se rychlost takové změny vyjádří poměrně snadno. Vektory se z jednoho bodu do druhého dají přemístit prostou translací. Z bodu p vyrazíme ve směru u a bude nás zajímat, jak rychle se vektorové pole mění v závislosti na čase t. Tedy jak silné pole naměříme v bodě q = p + tu vzhledem k hodnotě v bodě p (tj. jaký je rozdíl příslušných vektorů). A protože jsme si řekli, že tato změna závisí nejen na vektorovém poli V, ale i na směru u, přidám ho do závorky k tradičnímu diferenciálnímu symbolu „nabla“ (v učebnicích ho uvidíte jako subscript).
∇(u)V ~ (V(q) - V(p)) / t = (V(p + tu) - V (p)) / t
Ta poněkud mystická veličina ∇(u)V je stále vektorem (rozdíl vektorů vydělený skalárem) a pokud si ji představíte pro dostatečně malý čas t (můžete si tam místo t klidně napsat dt), dostanete v podstatě to, čemu říkáme derivace (tj. relativní změna) vektorového pole V ve směru u (směrová derivace). I bez znalosti diferenciálního počtu tu derivaci ∇(u)V můžete odhadnout tím, že do vzorečku budete dosazovat menší a menší hodnoty t a sledovat, k jakému vektoru se ten podíl blíží.
Na varietě M ovšem tento vzoreček vyhoří. Jednak při pochodu podél tečného vektoru u opustíme – společně s tečným prostorem – varietu (pokud bude u dostatečně dlouhý, dostaneme se až někam do stratosféry, kde je směr větru obvykle úplně jiný), ale hlavně není jasné, jak porovnávat (natož odečítat) vektory V(p) a V(q), které leží v úplně odlišných tečných prostorech.
My bychom potřebovali – stejně jako v eukleidovském prostoru – ten vektor V(q) nějak opatrně přemístit do bodu p a tam ho porovnat s vektorem V(p). A k tomu právě slouží paralelní přenos, který dává pozor, aby nám během přemístění nějaký trouba do toho opatrně transportovaného vektoru nedrknul.
Minule jsme ten transport realizovali tak, že jsme po varietě M tahali sáňky s hráběmi (ano, „s hráběmi“, to je na pokroucené varietě zcela adekvátní gramatický tvar).
Matematika na to ale spoléhat nemůže – co kdyby na varietě už 14 dní nesněžilo. A tak si vymyslela speciální identifikaci, pomocí které budeme schopni rozhodnout, které vektory z tečného prostoru TpM odpovídají kterým vektorům z tečného prostoru TqM.
Této identifikaci se v diferenciální geometrii říká afinní konexe a můžete si ji zhruba představit jako určité zobrazení, které říká: jo, tak tomuhle vektoru z TpM odpovídá tamhleten vektor z TqM. Historicky tento pojem vznikl z toho, že podél křivky valíte jednu a tu samou tečnou rovinu (jak je vidět na wikipedii) a snažíte se odhadnout, jakou stopu vaše křivka v rovině udělá – ta stopa vám prozradí, jak tečné vektory přenášet. Konexe tedy v jistém smyslu supluje eukleidovskou translaci a obvykle funguje lokálně, tj. porovnává tečné prostory v dostatečně blízkých bodech p a q.
Inu, ani na varietě se bez konexí nikam nedostanete.
Takových zobrazení je obecně hafo: můžeme například vektory z TpM při „převalení“ do TqM nenápadně trochu „přifouknout“ a stále dostaneme poměrně solidní vzájemnou identifikaci. Proto od těch konexí vyžadujeme, aby se chovaly rozumně (např. aby zachovávaly metriku), a pak se dá ukázat (a je to dokonce Fundamentální věta riemannovské geometrie), že taková „rozumná konexe“ existuje právě jedna. Říkáme jí Levi-Civitova konexe a právě ona nám technicky zprostředkuje to, čeho jsme minule docílili taháním sáněk po varietě. Tedy paralelní přenos.
To, že něco existuje (konexe), nám ale samozřejmě neříká, jak to spočítat. Na to si matematici vymysleli pěknou kulišárnu. Místo, aby nám dali nějaké zobrazení mezi dvěma tečnými prostory, ze kterého bychom si pak mohli směrové derivace ∇(u)V spočítat, tak oni nám rovnou dali ty směrové derivace. Konexe se tedy realizuje jako operátor ∇, což je jakási komplikovaná funkce, do které vhodíte vektorové pole U (obsahující váš směr u), vektorové pole V (jehož změnu se snažíte vyčíslit) a na výstupu vám vypadne příslušná směrová derivace ∇(u)V.
Jen se musí trochu upravit její definice, aby zahrnovala nejen to, jak se mění vektorové pole během našeho pochodu po varietě, ale i to, jak se mění souřadnice (např. na sféře se zeměpisná délka na rovníku mění podstatně pomaleji než na polárním kruhu, jak jsme viděli výše). Zhruba si ji můžete představit tak, že běžnou eukleidovskou směrovou derivaci promítnete v každém bodě p do tečné roviny TpM.
Takto vylepšené „směrové“ derivaci se říká kovariantní derivace vektorového pole a při studiu chování vektorových polí na varietách hraje zcela zásadní roli (mnoho autorů používá termíny „afinní konexe“ a „kovariantní derivace“ téměř jako synonyma, přestože konexe je o něco obecnější: je definovaná pro dvě vektorová pole U a V, zatímco kovariantní derivace už je v podstatě vyčíslená pro konkrétní vektor u z vektorového pole U).
Výpočet kovariantních derivací ovšem není žádná procházka růžovým sadem, protože kromě měnícího se vektorového pole V musíme bedlivě pozorovat i měnící se souřadnice. Jejich chování je zakódováno do tzv. Christoffelových symbolů, které jsou algebraickou reprezentací derivací bázových vektorů a najdete je prakticky v každém důležitém „křivočarém“ výpočtu – ať jsou to kovariantní derivace, geodetiky nebo tenzory křivosti (kdo se nebojí derivací, může se mrknout na toto zajímavé video).
Pro nás je ale směrodatné, že všechny tři pojmy – paralelní transport, kovariantní derivace a afinní konexe – jsou třemi různými aspekty téhož problému: jakým způsobem rozumně identifikovat vektory ze dvou sousedních tečných prostorů, abychom mohli nějak monitorovat měnící se vektorová pole (a obvykle můžete z jednoho pojmu odvodit ty ostatní).
Při paralelním přenosu v eukleidovském prostoru musíme dávat pozor, aby se nám jejich souřadnice neměnily, tj. požadujeme, aby měly nulovou derivaci. Na varietách musíme při přenášení podél křivek obdobně sledovat kovariantní derivaci: paralelně transportovaný vektor má nulovou kovariantní derivaci v tečném směru křivky. Z této charakterizace se pak dají odvodit další důležité pojmy.
Geodetika se dá například definovat jako křivka, která paralelně přenáší svůj vlastní tečný vektor, tj. pole T definované tečnými vektory (směrem sáněk) má v tečném směru nulovou kovariantní derivaci: ∇(t)T = 0. To pak vede k návodu, jak takovou geodetiku najít pomocí Christoffelových symbolů. Postup je to sice velmi technický, ale stále jednodušší než zkoumat délky všech možných křivek mezi dvěma blízkými body a snažit se najít tu nejkratší.
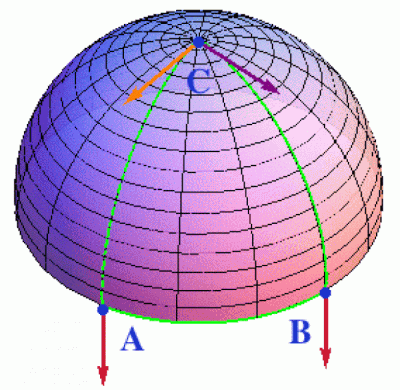
Koho ještě nebolí ukrutně hlava, může si dát jako nášup Riemannův tenzor křivosti, který je zobecněním konceptu Gaussovy křivosti do více-rozměrných prostorů. Jeho definice vychází z toho, co jsme viděli minule: v zakřivených prostorech závisí směr paralelně přenášeného vektoru na křivce, podél které ho přenášíme. Na obrázku vpravo vidíme malou modifikaci našeho původního experimentu.
Vystartujeme z bodu A do bodu C a budeme přenášet červený vektor. Pokud se do bodu C dostaneme přímo, výsledný vektor bude oranžový. Pokud to vezmeme oklikou přes B, bude fialový. A dá se ukázat, že míra odlišnosti obou vektorů závisí na průměrné křivosti naší variety uvnitř oblasti ohraničené našimi trasami. A od toho se odvíjí Riemannova konstrukce.
Abychom ale nemuseli vektor na sáňkách tahat až na rovník, provedeme celou operaci lokálně v okolí nějakého bodu p. Za směry si zvolíme dvě vektorová pole U a V (viz další obrázek) a budeme přenášet červený vektor w nejprve ve směru U a pak ve směru V po trase ABD (čímž dostaneme oranžový vektor w') a pak obráceně – nejprve podél V a pak podél U po trase ACD (čímž dostaneme fialový vektor w''). A ten rozdíl mezi nimi nám poslouží k definici Riemannova tenzoru křivosti R.
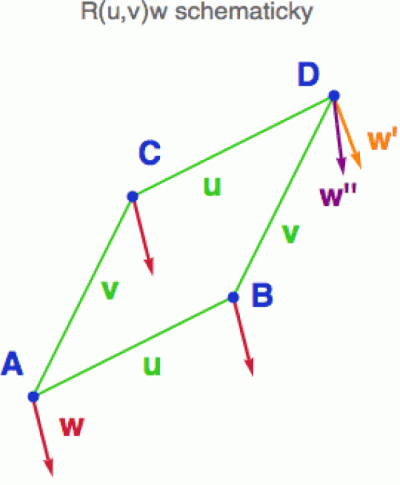
V infinitezimálním tvaru (tedy v případě, že přenášíme po velmi krátkých křivkách) se dá přenesený vektor vyjádřit pomocí kovariantních derivací (viz wikipedia). Zhruba řečeno, přenesený vektor je původní vektor plus změna (vyjádřená kovariantní derivací). Oranžový vektor bude mít tvar:
w' = w + ∇(V)∇(U)w
zatímco ten fialový bude mít pořadí derivací obráceně:
w'' = w + ∇(U)∇(V)w
Rozdíl těchto vektorů v podstatě definuje Riemannův tenzor křivosti (aplikovaný na vektor w ve směru polí U a V)
(#) R(U,V)w = w''- w' = ∇(U)∇(V)w - ∇(V)∇(U)w
Abychom zjistili jeho řád (tedy kolik vektorů potřebujeme na to, abychom z něho vyždímali skalár), budeme muset ten rozdílový vektor R(U, V)w, který z diferenciálního bludiště vyleze, ještě skalárně pronásobit dalším vektorem (přesněji kovektorem), takže celkově dostaneme řád 4 (přesněji (3, 1)). K určení komponent Riemannova tenzoru proto budeme potřebovat 4 indexy R(i, j, k, l). Je to tedy podstatně komplikovanější živočich než matice – tenzor 2. řádu – kde si vystačíme se dvěma: A(i, j).
(Z pohledu diferenciálního počtu tenzor vyjadřuje míru nekomutativity směrových derivací podle U a podle V, což kontrastuje například s tradičními parciálními derivacemi, které si vesele komutují – tedy nezáleží na tom, v jakém pořadí je bereme. S tím se ale normální smrtelník nemusí trápit – stejně jako s tím, že jsem v rovnici (#) zanedbal jeden extra člen vyjadřující to, že i směrová pole U a V se během operace trochu mění. Kdo se chce s Riemannovým tenzorem opravdu popasovat, nechť se mrkne na toto video.)
Celá tahle strašlivá nestvůra R(U, V)w řádí v Einsteinových rovnicích gravitačního pole. Tu starou dobrou gaussovskou křivost zavlekla docela daleko. Přesto tam trocha příbuznosti je. Ekvivalentem Gaussovy (dvourozměrné) křivosti je ve vícerozměrných prostorech tzv. sekční křivost K(u, v). Dobereme se k ní tak, že si v tečném prostoru (také vícerozměrném) vybereme 2D rovinu určenou vektory u a v a ta nám na varietě vysekne 2D podvarietu (stejně jako když si v tečném prostoru ke sféře vyberete 1 vektor a ten vám na ní vysekne 1D křivku). Sekční křivost K(u, v) je pak Gaussova křivost této 2D podvariety. A ta už s Riemannovým tenzorem R úzce souvisí, resp. se z něho dá explicitně odvodit. Kdo se rád kochá zapařenými vzorečky, může si tuto souvislost prohlédnout zde.
Douška
Jaká je tedy geometrie vesmíru? Když se podíváte na Einsteinovy rovnice gravitačního pole, naleznete na pravé straně tenzor energie a hybnosti T, který popisuje rozložení hmoty, zatímco na levé straně je kombinace metrického tenzoru G a Riemannova tenzoru R (přesněji jeho zúžené formy zvané Ricciho tenzor), tj. veličin popisujících geometrii prostoru.
Hmota tedy prostor nijak neohýbá v běžném slova smyslu. Pouze určuje jeho geometrické vlastnosti prostřednictvím tenzorů na levé straně. A stejně jako jsme výše viděli, že zcela plochá komplexní rovina se při vhodné definici metriky dokáže odít v geometrii odpovídající zakřiveným plochám, tak může náš vesmír při zkoumání přesného tvaru geodetik vyjevit, že jeho geometrie se neřídí eukleidovskými zákony. Světlo je známý lenoch a jakmile zjistí, že v prostoru jsou křivky (geodetiky), které jsou kratší než běžné přímky, hned na ně hupne. Na to není potřeba, aby se prostor fyzicky křivil. Stačí pozměnit metriku. A ta je – dle Einsteinových rovnic – ovlivněna rozložením hmoty.
Když si vezmete list papíru a trochu ho ohnete, plošníci v něm žijící to vůbec nezjistí, protože metrika a Gaussova křivost se vůbec nezměnily. Z jejich pohledu je úplně jedno, zda jste papír ohnuli málo, hodně nebo vůbec. Pro ně bude vesmír stále eukleidovská rovina, a to, jak je konkrétně vnořena do nějakého vyššího prostoru (zde 3D) pro ně nemá žádné praktické důsledky (ledaže byste ho srolovali do válce a umožnili jim vesmír obeplout). Stejně tak jsou pro nás směrodatné pouze geometrické vlastnosti našeho časoprostoru, ne to, zda se náhodou nekřiví v nějaké extra dimenzi, kterou pravděpodobně nikdy nezaregistrujeme (stejně jako plošníci nikdy nezaregistrují osu z).
Známe-li tedy rozložení hmoty, můžeme z něho v principu spočítat tenzory definující geometrii časoprostoru a z nich pak chování geometrických objektů – počet rovnoběžek, součet úhlů v trojúhelníku, odchylky během paralelního transportu vektorů podél uzavřených křivek atd.
Minule jsme viděli, že na zeměkouli, přestože její geometrie je globálně vzato sférická, existují lokálně všechny tři typy geometrií: sférická (např. na Řípu či uprostřed oceánu), hyperbolická (v horských sedlech) a eukleidovská (na plochách pečlivě vyválcovaných do roviny). S vesmírem se to má podobně.
Z lokálního rozložení hmoty můžeme usoudit pouze na lokální geometrické vlastnosti prostoru. Tedy jak se geodetiky, trojúhelníčky či přenášené vektory chovají lokálně v naší vesmírné kotlince. To nám, pochopitelně, nic neříká o globálním tvaru vesmíru (stejně jako horské sedlo nijak neindikuje to, že žijeme na sféře). Na to, abychom jej mohli studovat, bychom museli poměrně přesně změřit rozložení hmoty v celém vesmíru a to je zatím nad naše síly.
Momentálně se zdá, že náš vesmír je globálně plochý (s lokálními odchylkami danými rozložením galaxií). Vypadá tedy zřejmě jako taková velmi mírně zvlněná nekonečná rovina (s občasnými krtinami černých děr). Ovšem odhadnutá hustota hmoty celého vesmíru se blíží kritické hodnotě oddělující hyperbolickou a sférickou geometrii, takže na konečný verdikt si ještě budeme muset počkat. Dokonce se tu a tam objevují náznaky, že by vesmír možná mohl být globálně sférický (a tudíž pravděpodobně konečný). Tak uvidíme. Cenu piva to ale pravděpodobně neovlivní.
Článek je redakčně upravenou verzí blogového příspěvku na serveru iDNES.cz. Publikováno s laskavým svolením autora. Další díly a původní texty jsou dostupné na blogu Jana Řeháčka.