Jedním z nejzajímavějších přístupů ke strojovému učení jsou tzv. umělé neuronové sítě, které se snaží najít inspiraci pro svou vnitřní architekturu ve fungování lidského mozku. Tudy také vede jedna z cestiček k umělé inteligenci.
Lidský mozek obsahuje téměř sto miliard navzájem propojených neuronů. To je výpočetní a zpracovávací síť nepředstavitelné komplexity. Pro srovnání: nás lidí je na světě řádově deset miliard (za pár let to bude přesně) a naše vlastní interakce vytvářejí natolik komplikovaný systém, že z toho člověka při sledování večerních zpráv nejednou rozbolí hlava.
Jak přesně lidský mozek funguje, nevím, a nemám nejmenší ambice neurobiologům a psychiatrům kecat do řemesla. Já si ho – jako většina laiků – představuji jako 3D konfiguraci neuronů, které si mezi sebou nějakým způsobem předávají elektrochemické signály a umožňují tak mozku zpracovávat nejrůznější vstupní podněty, kontinuálně produkované našimi smysly. A toto schéma se přes svou naivitu stalo základem jedné z nejúspěšnějších podoblastí strojového učení poslední dekády: umělých neuronových sítí (ANN).
Neuronové sítě pro běžné problémy mívají stovky až tisíce neuronů, ale výpočetní technika postoupila do té míry, že na obtížnější problémy jsme schopni nasadit (a vytrénovat) neuronové sítě obsahující miliony – a v posledních letech už i miliardy – neuronů, takže se pomalu přibližujeme parametrům lidského mozku. Samozřejmě pouze v hrubém počtu. Zatímco umělý neuron je v podstatě algoritmický procesor, který načte vstupní signály a přetaví je ve výstupní signál, lidský neuron je sám o sobě taková malá biologická továrna na absolutno. Nicméně pokrok se nedá zastavit a už teď se hovoří o sítích obsahujících biliony neuronů, které budou schopny zpracovávat informace na velmi netriviální úrovni – proto se také této oblasti strojového učení někdy říká „hluboké učení“ (deep learning).
Současně nám neuronové sítě svými schopnostmi a způsobem zpracování informací umožňují pochopit některé dílčí funkce našeho vlastního mozku. Abych ale nezabředl do kontroverzních bažin filozofických problémů, soustředím se opět na matematiku. Zcela stranou ponechám otázku, zda sami nejsme pouze mimořádně komplikovaná neuronová síť, která přichází na svět s určitým zabudovaným hardwarem a od samého počátku se musí nějak vyrovnávat (rozuměj přepočítávat své parametry) se vstupními veličinami, jež se na nás prostřednictvím smyslů řítí s intenzitou tropického lijáku. A zatímco my starší už jsme se tak nějak naučili většinu těch informačních bouřek ignorovat, takový čerstvý novorozenec z toho musí být úplně paf.
Než začneme louskat lineární algebru, musím se přiznat, že čím víc neuronové sítě poznávám, tím menší prostor pro naši svobodnou vůli vidím. I bez znalostí softwarového inženýrství není možné si nepovšimnout určitých vzorců chování, které nás odnepaměti do jisté míry svazují. A fungování neuronových sítí některé jejich aspekty osvětluje. Zda je ovšem možné s jejich pomocí nasimulovat i abstraktnější formy rozhodování – např. morálku – to raději ponechám k posouzení odborníkům.
Jednoduché neuronové sítě
Neuronové sítě patří k metodám učení s učitelem a to znamená, že se pokouší najít nějakou souvztažnost (převodovou funkci F) mezi vstupními hodnotami x (obvykle atributy nějakých objektů) a výstupními hodnotami y (identifikační „nálepky“ těchto objektů).
Za tím účelem si příslušný software načte tréninkovou matici T, obsahující n příkladů dvojic (x, y), a stejně jako v metodách popsaných minule se z nich snaží odvodit obecný návod, jak hodnoty y určovat z hodnot x. Tento návod pak softwaru umožní odvozovat další hodnoty y autonomně – bez pomoci „učitele“ – pouze z hodnot x.
Abychom měli před očima něco konkrétního, vezměme si regresní model, kdy budeme určovat cenu domu (y) ze tří atributů: celková výměra (x1), vzdálenost od centra města (x2) a průměrný plat v daném okrese (x3).
Neuronové sítě se obvykle skládají ze vstupních neuronů (jejichž počet odpovídá počtu atributů – v našem případě 3), ze skrytých neuronů (těch můžete mít, kolik chcete) a z vrstvy výstupních neuronů (jejichž počet odpovídá dimenzionalitě prostoru nálepek – v našem případě 1). Skryté neurony (červené) jsou obvykle rozdělené do několika vrstev s tím, že všechny neurony předchozí vrstvy jsou propojeny se všemi neurony vrstvy stávající (v našem případě jsem zvolil tři vrstvy se 3, 2 a 4 neurony). Schematicky je taková síť naznačena na dalším obrázku (technicky se jí říká MLP; multilayer perceptron).
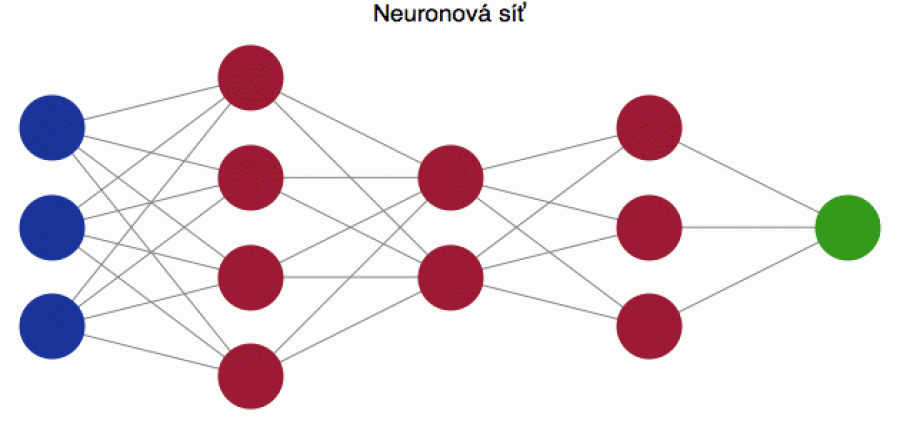
Pokud bychom měli 5 atributů, tak by modrá vstupní vrstva obsahovala 5 neuronů. A pokud by naše nálepky y byly 3D, tak by zelená výstupní vrstva obsahovala 3 neurony. S takovými nálepkami bychom se setkali např. při klasifikaci objektů do 3 tříd (pejsek-kočička-prasátko), kde by výstupní nálepky y = (y1, y2, y3) ukazovaly pravděpodobnost, zda se zkoumaný objekt nalézá v 1., 2. nebo 3. třídě.
Mechanika fungování neuronové sítě (zleva doprava) je vcelku jednoduchá. Vstupní hodnoty x se „připojí“ na vstupní neurony, ty pak na základě těchto hodnot „vystřelí“ sérii numerických signálů, která se šíří po síti a nakonec se zastaví na výstupních neuronech, ze kterých se odečtou jejich číselné hodnoty (to budou naše „předpovězené“ nálepky y). Každý neuron v podstatě přijme (ovážené) signály svých předchůdců, po sečtení je prožene nějakou nelineární funkcí a pošle je dál „po proudu“ svým následovníkům.
Než se neuronům podíváme podrobněji na zoubek, řekneme si pár slov o tom, jaké signály se tou sítí vlastně šíří. Jsou to v zásadě obyčejná reálná čísla odvozená ze vstupních atributů. Protože však budeme reálná čísla v průběhu tréninku různě kombinovat, je potřeba je nejprve normalizovat, abychom nesčítali hrušky s jablky. Atributy se mohou řádově lišit (např. výměra může být v desítkách m2, zatímco průměrný plat v desetitisících Kč), takže by jejich algebraické kombinace v syrovém tvaru nedávaly moc smysl. Proto se prakticky všechny atributy nejprve nějak transformují – např. aby výsledné bezrozměrné hodnoty ležely zhruba v intervalu (-1, 1).
Každý neuron je v podstatě autonomní výpočetní jednotkou, která si načte vstupní hodnoty z předchozích neuronů, nějakým způsobem je semele (obvykle tak, že prostě sečte příslušná čísla a součet prožene nějakou nelineární funkcí) a tuto „semletou“ hodnotu pak „vystřelí“ na výstupu, který se současně stává vstupem pro další vrstvu neuronů (s tímto neuronem spojených).
Jeden takový neuron máme na dalším obrázku vpravo. Nelineární funkci se říká aktivační a je schematicky znázorněna čtverečkem. Jejím posláním je zprostředkovat větší kontrolu nad funkcí každého neuronu. Hodit na výstup prostý součet vstupních hodnot je příliš jednoduchá možnost, která by mohla vést k numerickým nestabilitám (pro masivní sítě by součet mohl v některých neuronech rychle narůst a dominoval by celému výpočtu). Takto můžeme například simulovat situaci, kdy neuron až do určité kritické hranice nedělá nic (na výstup vyhazuje 0), a teprve pokud vstupy kritickou hranici překročí, tak začne emitovat nenulové hodnoty.
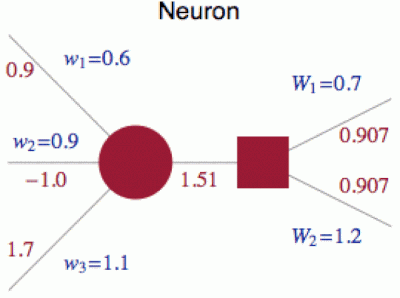
Funkce každého neuronu má tedy dvě fáze: jednu lineární (sečtou se příchozí signály) a jednu nelineární (signál se prožene aktivační funkcí A). V nákresech se však dvě fáze obvykle slijí, takže na diagramech vidíte pouze kolečka.
Aktivačních funkcí je celá řada a často se v různých vrstvách používají různé funkce podle typu úlohy. Nicméně v průběhu výpočtu už se aktivační funkce nemění. Zvolíte si je na začátku, při designu architektury sítě, a pak už se s nimi nehýbá.
To, s čím se hýbá (a v tom spočívá kouzlo neuronových sítí), jsou nastavitelné váhy (na obrázku označené modře: w a W) všech neuronových spojení, které simulují skutečnost, že ne všechna spojení mezi neurony jsou stejně významná. Když např. spodní neuron v předchozí vrstvě vyšle signál, tak neuron na obrázku jeho výstup pronásobí číslem w3 = 1.1.
Náš neuron tedy zachytí signály svých předchůdců a posčítá je s příslušnými váhami w: .9 * 0.6 - 1 * 0.9 + 1.7 * 1.1 = 1.51. Vybereme si aktivační funkci, řekněme A(x) = tanh(x), a její aplikací získáme výstupní signál tanh(1.51) = 0.907, který pošleme dalším neuronům v síti. Ty ho zachytí a po pronásobení váhami W posčítají s výstupy ostatních neuronů (zatím si ty váhy představujte jako fixovaná čísla vyjadřující vlastnosti dané neuronové sítě).
No a takto se vstupní signály vesele šíří sítí, a nakonec jsou odečteny v poslední (zelené) vrstvě jako síťové výstupy y', které nám umožňují regresi či klasifikaci. V našem případě by se z hodnoty y' určila předpovězená cena domu.
Jistě vám neuniklo, že to koumání, který neuron je spojen se kterým a jaké ma dané spojení váhu, je pro praktické počítání trochu matoucí a nepohodlné. Proto se v praxi používá maticový přístup. Pokud máme třeba ve druhé vrstvě k2 neuronů a ve třetí k3 neuronů, pak se všechny výstupy z 2. vrstvy prostě označí vektorem x2 (který má dimenzi k2). Ovážené vstupy do třetí vrstvy pak odpovídají k3-dimenzionálnímu vektoru x3, který se spočítá maticovým vynásobením x3 = W.x2, kde převodová matice W typu k3xk2 v sobě obsahuje informaci o všech váhách mezi 2. a 3. vrstvou. Pro citlivější odezvu se na pravou stranu převodové rovnice ještě někdy přidává vektor b (tzv. bias), jehož hodnotu je nutno odvodit – stejně jako váhové matice – během optimalizace. Tím je lineární fáze vyřízená a v té nelineární se všechny složky vektoru x3 proženou aktivační funkcí a pošlou dál do 4. vrstvy sítě.
Toto celé je snadnější částí celého procesu, které se říká dopředná propagace (forward propagation). Další hezký příklad s výpočtem naleznete zde.
Něco tomu všemu ale schází. Zatím jsme si vzali tréninkovou množinu dvojic (x, y), pro každý vstup x jsme spočítali síťový výstup y' a ten porovnali se vstupem skutečným y. Ale protože parametry naší sítě (váhy w) jsme zatím zvolili zcela náhodně, není důvod očekávat, že výstupní y' budou jakkoliv připomínat skutečné hodnoty y (což je naším cílem). Toho se docílí teprve pilným tréninkem (stejně jako když se učíte slovíčka – pokud začnete z hlavy jen tak náhodně tahat české významy, budou pravděpodobně špatně).
Teď se podívejme na to nejdůležitější. Úkolem naší sítě je simulovat funkci F, která převádí vstupy x na výstupy y. Nahodile sestavená síť v tomto ohledu pochopitelně moc nezáří. A tak se nabízí myšlenka, co kdybychom ty váhy začali různě štelovat (měnit) tak, aby se rozdíly mezi síťovými výstupy y' a očekávanými výstupy y postupně zmenšovaly?
A přesně toto je cílem trénování neuronových sítí: z původní náhodné ovážené sítě se pokusíme vyždímat síť, které se podaří (alespoň pro tu tréninkovou množinu T) očekávané výstupy y poměrně přesně aproximovat těmi síťovými y'. To si obvykle vyžaduje několik desítek až stovek iterací, během nichž se sítí proženou všechny vstupy x a trpělivě se seřizují váhy.
Podobně jako minule si označíme chybovou funkci (pro dané váhové parametry w)
error(w) = ∑ |y-y'|
Pár technických poznámek: součet je přes všechny vstupy x tréninkové matice T; místo absolutní hodnoty bych samozřejmě mohl použít i klasickou odmocninu ze součtu čtverců; správně bych měl napsat y'(w), protože síťové výstupy samozřejmě závisí na w; a konečně písmenko w označuje všechny váhové matice mezi vrstvami (plus případné biasy), takže těch parametrů (proměnných) chybové funkce je hodně – řádově tisíce až miliony.
No a zbytek seřizování je opět pouze optimalizační úloha. V mnohodimenzionálním prostoru W se snažíme najít hodnotu váhových parametrů w0, pro které bude uvedená chyba minimální. A to se provede (jak jsme viděli v minulé sekci Jauvajs) nějakou gradientovou metodou. Jen to má malý háček.
Abychom k tomu minimu mohli úspěšně sestoupit, potřebujeme znát gradient chybové funkce a to znamená, že potřebujeme vědět, zda se chyba bude zvětšovat nebo zmenšovat, pokud budeme zvětšovat nebo zmenšovat danou váhu. Technicky řečeno, potřebovali bychom vědět, jaká bude parciální derivace (rychlost změny) chybové funkce error(w) vzhledem k dané váze w.
Ta se dá poměrně dobře odhadnout pro váhy v poslední vrstvě, kde už nemáte žádné další neurony v cestě. V tomto případě se dá explicitně spočítat, jak se chyba zachová, pokud s váhou trochu pohnete tím či oním směrem. Jakmile máte derivace pro finální vrstvu odhadnuté, přesunete se „proti proudu“ sítě k předchozí vrstvě a odhadnete derivace pro její váhy (tady už musíte používat derivace složené funkce, protože chyba z předposlední vrstvy vznikne složením s chybou z vrstvy poslední, a to přes všechny možné cesty k výstupní vrstvě).
Takto postupně – odzadu dopředu (zprava doleva) – odhadnete parciální derivace chybové funkce pro váhy ze všech vrstev. A můžete začít optimalizovat, tedy sestupovat k minimu. Tomuto poměrně technickému a úmornému výpočtu (na kterém jsou ovšem schopnosti neuronových sítí postaveny) se říká zpětná propagace (back propagation).
Naštěstí už ji dnes za vás udělají specializované softwarové knihovny, takže pokud vás zajímají pouze praktické aplikace, nemusíte si s jejími krkolomnostmi lámat hlavu (tady je celkem praktický návod, jak si celou věc naprogramovat).
Dvouduché neuronové sítě
Ty jednoduché neuronové sítě dokáží vyřešit spoustu problémů, ale pro určité typy úloh je jejich konstrukce příliš strnulá. Vstupní informace se do první vrstvy vkládají vždy ve stejném pořadí, např. první neuron vždy snímá z trénovací množiny výměru domu, druhý vzdálenost od centra a třetí průměrný plat v okolí. To je na jednu stranu výhodné, protože síť se na tyto vstupy dokáže připravit a dokáže je následně efektivně zpracovat, ale na druhé straně to síti zabraňuje pružně reagovat na dvě důležité okolnosti.
Za prvé: Vstupní atributy nemusejí být nutně nezávislé, ale mohou tvořit smysluplnou posloupnost, ve které jejich pořadí nese nezanedbatelnou část informace. Pokud například analyzujeme věty, pořadí slov je důležitým vodítkem pro stanovení významu věty. Zatímco v předchozí sekci jsme na vstup položili jakýsi košík náhodně poskládaných atributů, gramatická věta představuje – co se týče pořadí – poměrně rigidní útvar. První slovo dané věty nemůžeme jen tak mýrnix týrnix šoupnout na konec. Proto je potřeba navrhnout strukturu, která se dokáže podívat nejen na momentálně vkládané slovo, ale i na slova předchozí.
Za druhé: Kruciální informace se může nalézat na různých pozicích vstupního souboru dat. Pokud například klasifikujeme obrázky zvířat a snažíme se zjistit, co je pejsek a co kočička, zjistíme, že někdy je vlastní zvířátko v pravém horním rohu, jindy v levém dolním. Ty samé vstupní pixely tedy někdy nesou podstatnou informaci, a jindy nepodstatnou. Architektura sítě si musí poradit s tím, že pejsek či kočička se může nalézat v libovolném sektoru vstupních dat. Nemůžeme už tedy čekat, že daný kritický atribut bude vždy snímán z toho či onoho neuronu.
V obou případech vyvstává potřeba lokalizovat důležitou informaci a umožnit jí interakci s okolními prvky. Ať už je to v jednorozměrném kontextu, kdy je nutno do zpracování kromě vlastních hodnot vstupní sekvence zahrnout i vztahy mezi jejími jednotlivými členy, anebo v kontextu dvourozměrném, kdy se můžeme opřít o plošné vztahy ve vstupních datech.
Tyto požadavky vedly k designu dvou důležitých kategorií neuronových sítí.
Rekurentní neuronové sítě (RNN) se pokouší usnadnit zpracování sekvenčních dat a kromě analýzy textu se často používají pro zpracování mluvené řeči nebo časových řad (např. data z akciového trhu.
Jednoduchý design MLP z předchozí sekce je zjednodušeně zaznamenán v levé části následujícího obrázku. Vstupní data X procházejí skrytou částí sítě (v červeném) a nakonec se transformují do hodnot Y na výstupu (zde tedy body nereprezentují jednotlivé neurony, ale jejich kolekce). Další várka vstupních atributů je pak aplikována zcela nezávisle. Neexistuje zde žádný mechanismus, který by umožňoval komunikaci signálů mezi jednotlivými vstupy X. Otázka je, zda by se část informace ze skrytých komponent nedala recyklovat a použít pro zpracování v dalších krocích, jak je schematicky naznačeno v pravé části obrázku.
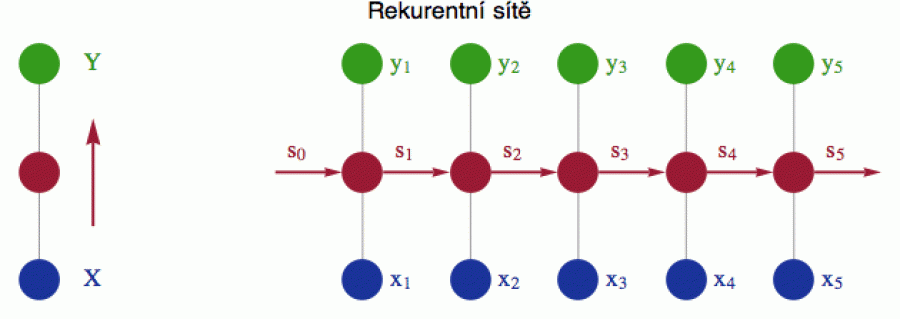
Taková struktura má dvě důležité výhody. Jednak síti umožňuje předávat si informaci mezi jednotlivými časovými kroky a jednak redukuje počet vstupních parametrů (váhy neuronových spojení). Většina rekurentních sítí totiž používá (v jednotlivých časových krocích) stejné převodové matice W, takže není nutno držet v paměti kupu obřích matic pro každý krok t = 1, 2, 3, 4, ... zvlášť.
Ta skrytá vrstva tedy přijímá nejen informaci ze vstupu, ale i z předchozí skryté vrstvy, takže lineární a nelineární fázi předávání signálu můžeme schematicky zaznamenat takto:
r(t) = W.x(t) + V.s(t-1)
s(t) = A(r(t))
kde r je mezisoučet před aplikací aktivační funkce, A je aktivační funkce, a V a W jsou převodové matice. Výstup se pak realizuje další převodovou maticí: y(t) = U.s(t)
(Mimochodem, v některých aplikacích, např. při analýze sentimentu vět ani není potřeba jednotlivé výstupy zaznamenávat, ale stačí zachytit ten poslední, který zahrnuje sentiment celé kolekce slov a který je de facto „zakódován“ v tom skrytém vektoru s.)
Předávání skrytých hodnot v jednotlivých časových krocích umožňuje síti naučit se efektivně používat i informace vložené v předchozích krocích. Struktura uvedená v pravé části obrázku je ale příliš primitivní a vede k některým numerickým problémům, a proto se v praxi používají o něco komplikovanější formy této myšlenky, např. LSTM buňky (long short term memory).
Mimochodem, víte, jak funguje překladač Google? V původní verzi se snažil pospojovat otrocky přeložené fráze, ale v posledních letech používá speciální architekturu rekurentních neuronových sítí, které se říká sekvence-na-sekvenci (seq2seq).
Naivně by si člověk mohl myslet, že se vezme RNN, na vstupy x(i) se nasekají české věty, na výstupy y(i) se posadí jejich anglické ekvivalenty a pak se během tréninku počítač naučí stanovit váhy převodových matic tak, aby to celé fungovalo co nejlépe. Problémem je, že odpovídající si věty mohou mít v různých jazycích různý počet slov. Např. na anglické „we are going home“ nám v češtině stačí dvě slova „jdeme domů“.
Takže si páni inženýři sestavili důmyslné spojení dvou nezávislých RNN (tzv. encoder-decoder). V té první se věty jednoho jazyka proženou sítí a jejich význam se zakóduje do skrytého stavu s. Ten se pak předá druhé větvi RNN a ta z toho skrytého stavu (což je mnohorozměrný vektor) vykouzlí sekvenci slov – ne nutně stejné délky – v druhém jazyce (ilustrační obrázek je zde).
Tímto způsobem se dají generovat například i automatické popisy obrázků. V první RNN převede software obrázek na skrytý stav s a ve druhé RNN se tento skrytý stav „rozbalí“ do sekvence slov. A váhy obou RNN opět stanovíme optimalizací: počítači ukážeme tisíce obrázků s popiskami a on si pak ty váhy sám seřídí tak, aby proces produkoval co nejméně chyb.
Problém práce s obrázky nás dovádí k druhé důležité skupině sítí.
Konvoluční neuronové sítě (CNN) nám umožňují zpracovávat data, jejichž přirozená struktura je dvourozměrná – např. obrázky, což jsou de facto matice pixelů.
Nejprve něco málo o konvoluci.
(abychom se vyhnuli integrování, ukážu vám zjednodušený příklad se
součtem)
Vezměme si posloupnost f = {1,2,3,4,5}. Pokud budeme chtít zjistit součty po sobě jdoucích čísel, což je lokální vlastnost posloupnosti f, můžeme si zadat tzv. konvoluční jádro g = {1,1,0,0,0} a jeho posunutou verzi (kdy posunujeme jedničky) pak přikládáme jako „masku“ k původní posloupnosti a počítáme skalární součiny. Dostaneme:
{1,2,3,4,5}.{1,1,0,0,0} = 3
{1,2,3,4,5}.{0,1,1,0,0} = 5
{1,2,3,4,5}.{0,0,1,1,0} = 7
{1,2,3,4,5}.{0,0,0,1,1} = 9
O posloupnosti vpravo f' = {3,5,7,9} pak říkáme, že vznikla konvolucí posloupnosti f a jádra g: f' = f✱g. Mohli jsme také přidat pátou hodnotu (tím, že bychom tu vpravo vypadnuvší jedničku zase vrátili na začátek), ale z pohledu CNN bude názornější, když výslednou posloupnost f' ponecháme „oříznutou“.
Sečteno a podtrženo, konvoluce je způsob, jak z daného objektu systematicky vyseknout podobjekt a provést na něm nějakou algebraickou operaci. A to je přesně to, co se CNN snaží udělat s obrázkem.
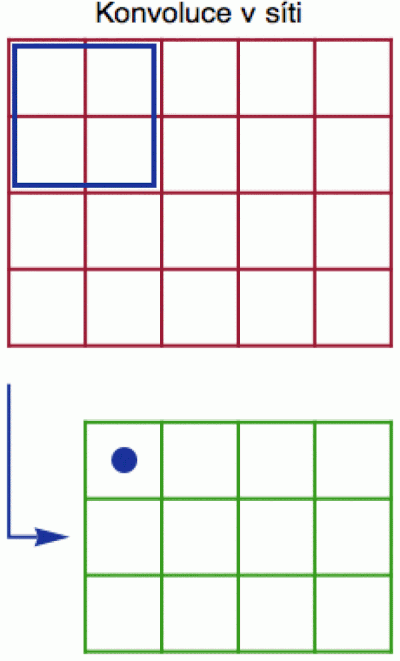
Vezměme si malý obrázek 5x4 pixelů (červený obdélník vpravo) a v něm si zadáme (modře) konvoluční jádro 2x2 pixely. Pro dvě jedničky nahoře jsme měli 4 možné polohy a výsledkem byla posloupnost 4 čísel. Podobně můžeme modrý čtverec posunout až o 3 pole horizontálně (máme tedy k dispozici celkem 4 polohy) a o 2 pole vertikálně (celkem 3 polohy). Výsledkem konvoluce tedy bude zelený obdélník 4x3. Každé jeho políčko odpovídá jedné poloze modrého konvolučního jádra. Jakým způsobem v něm vybarvíme políčka, bude záviset na tom, jakou algebraickou operaci si pro agregaci vybereme, můžeme například použít maximum hodnot pixelů uvnitř oblasti vymezené modrým jádrem, popřípadě jejich součet nebo cokoliv jiného (hezkou animaci tohoto procesu naleznete zde).
Hodně zhruba si 2D konvoluci můžete představovat tak, že modrý obdélník běhá po červeném, hledá obrázek pejska a výsledky si zapisuje do zeleného zápisníčku. To je ale trochu zavádějící, protože během algebraické operace se obrázek pejska samozřejmě rozmaže, ať byl tam či onde. Trochu přesnější vysvětlení je, že konvoluční operace se snaží v obrázku najít nějaké opakující se jednoduché motivy (např. hrany, zaoblené rohy atd.) a z jejich kombinací pak skládá další komplikovanější črty. Konvoluční jádro má spoustu parametrů (výška, šířka, zda se posunujeme jen o jedno pole nebo o víc, zda je původní obrázek „vyfutrován“, abychom se s modrým konvolučním obdélníkem mohli dostat za červenou hranici atd.), takže se nemusíme bát, že bychom neměli dostatek materiálu. Při tom využíváme skutečnosti, že konvoluční operace jsou (s vhodně definovanou algebraickou operací) translačně invariantní, takže jednoduché motivy dokáží najít kdekoliv (podrobnosti zde anebo zde).
CNN tedy fungují podobně jako běžné neuronové sítě, pouze s tím rozdílem, že se v prvních vrstvách snaží pomocí konvolučního hnětení rozšmelcovat vstupní pixelovou matici na abstraktnější atributy, z jejichž interakcí se následně (pomocí dalších skrytých vrstev) pokusí sestavit výstupní vektor, který obrázek nějakým způsobem charakterizuje.
Možných typů neuronových sítí je samozřejmě mnohem víc, ale pro začátek nám jednoduchý MLP a dvouduché CNN a RNN bohatě postačí. Pokud vás zajímá, k čemu se tyto sítě používají či nepoužívají, mrkněte sem.
Sekce Jauvajs: Overfit versus underfit
(pouze pro mimořádně otrlé povahy)
Člověk by řekl, že čím více neuronů do sítě naboucháme, tím přesnější predikci nám umožní dělat. Ale není tomu tak. Naše hledaná funkce F (která svazuje vstupy x s výstupy y) vychází z nějakých reálných dat či měření, a je tudíž zatížena chybou. A pokud zvolíme příliš komplikovanou architekturu, sítě se začnou učit ty náhodné odchylky, a ne závislosti, které má funkce modelovat.
Výsledný funkční model musí být tak trochu jako chytrá horákyně, ani moc jednoduchý, ani moc složitý. Přesněji, při hledání funkce F je důležité, z jaké množiny funkcí ji vybíráme. U lineární regrese to bylo jasné, hledali jsme F pouze mezi přímkami. V obecném případě je to obtížnější: množina funkcí musí být dostatečně bohatá, aby dokázala vyjádřit komplexitu našeho problému, ale nesmí být příliš bohatá, protože pak by stroj do svého vnitřního modelu zahrnul i ty nahodilé odchylky (např. vliv prostředí či měřicí aparatury) a to není žádoucí.
Podívejme se nejprve na jednoduchou regresní úlohu, která tento problém hezky ilustruje. Nejprve jsem si pomocí kvadratické funkce F a náhodných chyb („posunutí“) vygeneroval jednoduchá data (x, y), kdy se z jednoho atributu x pokoušíme předpovědět „nálepku“ y (tedy klasický regresní problém). Já funkci F ale stroji neprozradím a nechám ho, ať si ji sám objeví z „naměřeného“ datového souboru (červené bodíky níže). V dané množině funkcí tedy software hledá tu, pro kterou bude součet odchylek Σ(y-y') 2 minimální (y' je opět hodnota předpovězená modelem). Máme pouze jeden atribut x, takže si celou situaci můžeme demonstrovat na 2D obrázku.
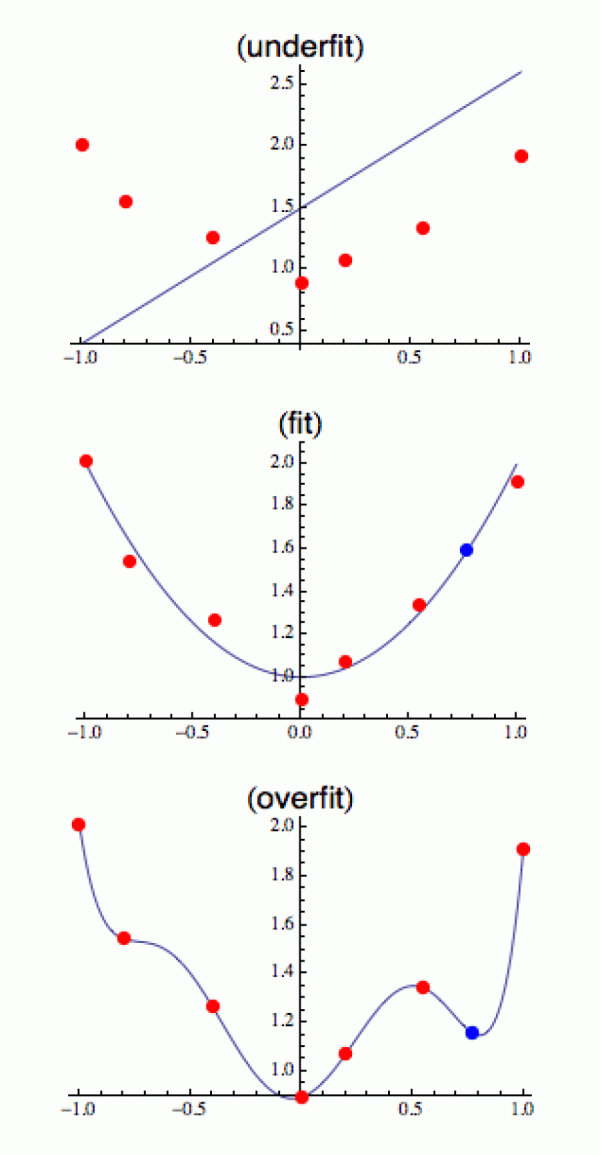
Na prvním obrázku se stroj snaží data aproximovat polynomy prvního stupně (přímkami). Už od pohledu je jasné, že data jsou zhruba kvadratická a žádná přímka (y = ax + b) nemá šanci je dostatečně přesně aproximovat, ať s ní kvedláme, jak chceme. Stroj jsme omezili na příliš chudou množinu (pouze přímky) a v rámci této množiny se konkrétní data nedají dobře popsat, takže výsledný algoritmus bude nepřesný (této situaci říkáme technicky underfit).
Na prostředním obrázku jsme množinu polynomů rozšířili na kvadratické. Ty mají o parametr víc (y = ax2 + bx + c) a s trochou práce se stroji podaří koeficienty navolit tak, že dostane obstojnou aproximaci. Díky ní dokáže solidně odhadnout hodnotu y i pro x mimo náš datový soubor. Prostě si načte novou x-ovou souřadnici a spočítá y' = ax2 + bx + c (modrý bod), který se od skutečné hodnoty y pravděpodobně nebude příliš lišit.
Povzbuzeni tímto úspěchem bychom mohli zkusit polynomy libovolného stupně. A ejhle. Na posledním obrázku se nám podaří bodíky proložit křivkou naprosto přesně (polynom 6. stupně). Zdánlivě máme ještě přesnější model reality. Jenže to má háček. Tento model se sice „naučil“ tréninkovou množinu bezchybně, ale když mu předhodíme nějaký nový bod x, tak předpověď selže. Když pro novou hodnotu x spočítáme y' a vyneseme do grafu (modře), vidíme, že jsme úplně mimo kvadratickou funkci, ze které jsem data vygeneroval (tuto situaci označujeme slovem overfit). Jinými slovy více parametrů neznamená nutně úspěšnější model reality!
Shrňme si to: problém spočívá v tom, že hledanou funkci F poznáváme pouze skrz datové body (x, y), které jsou zatíženy chybou, tj. jsou svázány vztahem y = F(x) + error. Pokud zvýšíme komplexitu modelu, velmi často se stane, že stroj tuto extra kapacitu využije k tomu, že se tréninková data doslova našprtá nazpaměť (i s tou chybou), ale hledanou závislost z nich nevyždímá (takže nebude schopen určit „nálepky“ nových, dosud neviděných, příkladů).
Asi nejmarkantnější je tento fenomén u rozhodovacích stromů (viz minulé Matykání). Je celkem jasné, že pokud položíme stroji dostatečný počet otázek, podaří se nám tréninkovou množinu popsat naprosto přesně (každý příklad pak má obvykle svůj vlastní „list“). Když pak ale strojem protahujeme dosud neviděné příklady, zjistíme, že putují do úplně nesprávných částí stromu, protože při jeho konstrukci některé otázky postihovaly spíše ty náhodné jevy než hledané souvztažnosti.
Když tedy obecně zvýšíme počet neuronů nebo stromových větví, neznamená to nutně větší přesnost modelu. Proto se testování algoritmu provádí na separátní testovací množině, kterou stroj během tréninku neviděl (a neměl tudíž možnost se ji našprtat). Proto mají některé algoritmy v sobě zabudované zpětné vazby, které se komplexitu modelu snaží držet na uzdě, např. během tréninku vyřazují některé neurony, omezují délku stromů anebo na parametry metody kladou omezující podmínky (tzv. regularizace).
Abychom toto dvojmatykání nějak uzavřeli, vraťme se k úvodnímu příkladu z minule. Tomu capartovi, který se učí rozlišovat domácí mazlíčky, přidáme paměťovou kapacitu (zvýšíme počet „parametrů“ jeho modelu), takže se náš malý „klasifikátor“ bude schopen maminkou vybrané příklady kočiček a pejsků přesně našprtat. Když uvidí kočičku, již dříve „naučenou“, tak ji samozřejmě správně klasifikuje jako kočičku. Jenže uvidí-li kočičku novou, bude na rozpacích, protože se nenaučil z předložených příkladů vyabstrahovat důležité atributy, které by mu umožnily predikci zatím neviděných příkladů.
Je to tak trochu, jako když se máte ve finštině naučit Archimédův zákon. Pokud vám profesor pokyne, abyste spustili, tak ho lehce odrecitujete (aniž byste tušili, o čem vlastně mluvíte). Jakmile vám ale zkoušející položí jakoukoliv doplňující otázku (notabene ve finštině), jste vedle jak ta jedle. V tom spočívá zrádnost šprtání. A proto je overfit problémem.
Jazyková douška: Slůvko „fit“ tady neznamená „fyzickou zdatnost“ (I am fit, because I exercise), ale „přiléhavost“ (This dress fits my body perfectly). Takže underfit znamená, že množina polynomů, ze které taháme funkci F, k dané množině přesně nepřiléhá, zatímco overfit znamená, že přiléhá až moc. A protože na prostředním obrázku se nám podařilo funkci F „napasovat“ na daná data tak akorát, mohli bychom fenomén na horním obrázku popsat českým slovem podpasovanost (underfit) a na spodním přepasovanost (overfit).
Článek je redakčně upravenou verzí blogového příspěvku na serveru iDNES.cz. Publikováno s laskavým svolením autora. Další díly a původní texty jsou dostupné na blogu Jana Řeháčka.