Tento historický citát hezky odráží tradiční nedůvěru veřejnosti ke statistikám. A nelze se divit. Politici si rádi statistiku ohýbají k obrazu svému. Přesto patří k důležitým nástrojům na cestě k pochopení moderní společnosti.
Můžeme-li věřit Marku Twainovi, výrok uvedený v dnešním titulku pronesl bývalý britský premiér Benjamin Disraeli (1804-1881) a vyjmenovává v něm tři typy lží.
Co ho k jeho soudu vedlo, nevím, faktem ale zůstává, že není nijak obtížné přizpůsobit statistickou metodologii politické objednávce (tj. masírovat data určitým směrem).
Možná znáte nějakou variantu Müller-Lyerovy iluze, ve které se nám stejně dlouhé úsečky jeví jinak podle grafického kontextu, v jakém je vidíme. Statistika je v podobné pozici. Pracuje sice s tvrdými daty, ale jejich sociologický účinek závisí na tom, jak se zasadí do kontextu a jak se vizuálně načechrají.
Možností k nenápadným podpásovkám je v komplikovaném zpracování dat více než dost. Tu se zapomene do nominálních výsledků započítat inflace, tu se nějaká kvantita normalizuje, řekněme, velmi kreativně a v případě nouze nejvyšší se vezme vzorek ne zcela náhodný (ve společenských vědách má většina rozdělení empirický charakter určený nějakou širší populací - jak vybrat malý vzorek, aby odrážel statistické vlastnosti celé populace co nejlépe, je poměrně obtížný úkol). Proto nepřekvapí, že statistika nemá zrovna křišťálově čistou pověst.
Na druhé straně jsou socio-ekonomické procesy natolik komplikované - a v mnoha ohledech téměř chaotické - že bez statistiky je prakticky nemožné vysledovat v moři individuálních hledisek, pocitů a zkušeností jakékoliv relevantní společenské trendy. Zkrátka statistika je jako oheň. Dobrý služebník, ale zlý pán.
Zatratit ji by bylo jako vylít s vaničkou i dítě. Není nutné znát všechny její technické finesy, ale je dobré vědět, jak funguje - kde má silné stránky a kde Achillovu patu. Vědět, co od ní lze očekávat a co nám prozradit nemůže, ani kdyby se rozkrájela na tisíc kvantilů.
Proč měl Mozart tak skromný pohřeb
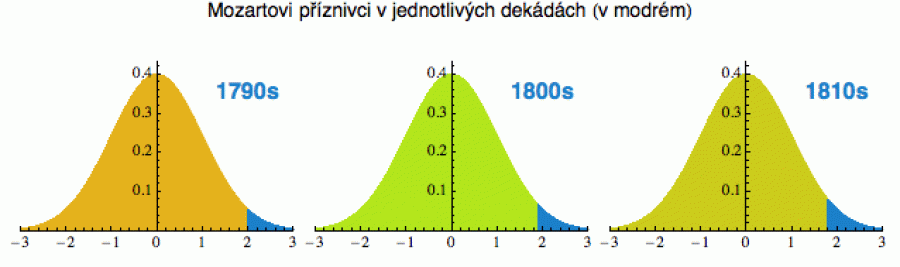
Okolnosti Mozartova pohřbu nejsou úplně známé a Formanova temná vize je pravděpodobně do jisté míry uměleckou licencí. V každém případě byl jeho pohřeb neokázalý a bez tradičních ceremonií (dnes by se to jistě neobešlo bez gigantické show globálního formátu). Mnozí ve Vídni o mladém géniovi věděli, mnozí něco tušili. Ale z pohledu statistiky jich bylo málo. Říkám tomu prokletí Gaussovy křivky.
Slavná kvadratická exponenciála ve tvaru zvonu nám říká, že u běžných náhodných proměnných najdeme nejvíce hodnot poblíž průměru. Ať už si vezmete výšku, váhu nebo IQ, drtivá většina populace se bude nalézat v úzkém pásmu kolem průměrné hodnoty. Výrazné výjimky - ať na tu nebo onu stranu - naleznete zřídka. A nejinak se to má i se schopností rozpoznat hudební talent. Ať chceme nebo ne, i v otázce hudebního cítění si většina z nás hoví někde uprostřed hypotetické Gaussovy křivky. A ruku na srdce - dokážete posoudit, co ze soudobé hudby se bude hrát ještě za 100 let? Já ne.
Jak to, že se tedy Mozart nakonec proslavil? Statistika nefunguje jen v jednom konkrétním čase T, ale sonduje veřejný vkus neustále. V jedné dekádě sice Mozarta zastíní kdejaký přičinlivý fidlal z císařského dvora, jenže v dekádě příští bude milá hvězdička du jour zapomenuta a nahrazena jinou, zatímco ti znalci v pravém cípu Gaussovy křivky si cestu k Mozartovi vždy najdou. A ta naakumulovaná popularita nakonec převáží.
A ještě jeden mechanismus hraje Mozartovi do not. Mezi posluchači se kromě
hudebních fajnšmekrů vyskytuje i typ, kterému říkám podfajnšmekr - tedy
někdo, kdo toho Mozarta sice neocení, ale zná se s lidmi, kteří jeho talent
rozpoznají, a protože chce být „in“, rád naskočí na znalecký
rychlík. Proto jsem ten Mozartův cípek nechal s časem trochu růst. Po čase
se z génia stane klasik a pak už to jde samo - přesně v intencích Werichova
výroku „na klasiky se nechodí, na klasiky se sluší chodit“.
Je to tak trochu, jako když se stěhujete. S každou novou štací se musíte probrat mořem haraburdí a rozhodnout, co vyhodit a co si ponechat. Opékač topinek se dá nahradit, svatební fotografie po babičce nikoliv. A jak se lidstvo přesouvá z jedné dekády do druhé, také si musí rozmyslet, co si s sebou dál potáhne v hudebním košíku. To, co vám složí momentální vládce hitparády, vám za deset let složí lépe někdo jiný. Mozarta už vám nesloží nikdo. A tak je nejlepším uměleckým soudcem nakonec čas. Respektive pár nadšenců, kteří tu kvalitu rozpoznají a pronesou ji do příští dekády.
A ještě malá technická zajímavost: to normální (Gaussovo) rozdělení má ve statistice zcela výjimečné postavení. Nejenže mu podléhá spousta náhodných veličin, ale existuje i věta, která říká, že pokud si vezmete několik náhodných veličin (ne nutně s gaussovským rozdělením) a zprůměrujete je, tak výsledek se bude řídit právě normálním rozdělením. Příslušnému tvrzení se říká centrální limitní věta.
Proč se nedokážeme shodnout v politice
Kdyby byl svět černobílý, žilo by se nám blaze. Přesně bychom věděli, kdo jsou padouši a kdo dobrodějové, a politika by se zredukovala na vyexpedování jedněch na Pankrác a druhých do Strakovky. Ale tak jednoduše to bohužel nefunguje.
Je kapitalista hodný, nebo zlý? Je imigrant líný, nebo pracovitý? Je církevní hodnostář osvícený, nebo tmářský? Intuitivně tušíme, že správná odpověď je - jak který. Na tom se asi všichni shodneme. Pokud si škálu mezi zmíněnými kladnými a zápornými vlastnostmi představíme jako interval od 0 (padouch) do 10 (klaďas), můžeme každému jednotlivci přiřadit nějakou číselnou hodnotu. Tenhle kapitalista je trojka (spíš zlý), zato tamhleten je osmička (docela hodný). Na čem se asi neshodneme, bude rozdělení těchto hodnot. Jsou kapitalisti převážně hodní, a nebo převážně zlí? To je, oč tu běží.
A protože dynamo politické tektoniky je poháněno statistickými vlastnosti daného souboru (tedy lidově - které vlastnosti převažují), pro posouzení socio-ekonomických problémů je důležité tato rozdělení znát, nebo je alespoň umět odhadnout. A v tom tkví kámen úrazu.
Každý z nás má jen velmi omezenou osobní zkušenost. Něco se sice dozvíme od lidí, kterým důvěřujeme, něco vyčteme z tisku (a tady už se vystavujeme propagandě), ale náš datový fond bude ve srovnání s reálným světem v jeho úplnosti téměř zanedbatelný.

Minule jsme viděli, že k odhadnutí rozdělení (a je jedno, zda si ho představujete jako rozdělení hodných a zlých kapitalistů, nebo líných a pracovitých imigrantů) potřebujeme dostatečný počet dat. Na obrázku vpravo vám ukážu příklad, jak matoucí obrázek vám nedostatečný soubor dat může podat. Vygeneroval jsem 10 datových sad ze zeleného rozdělení a na obrázku pak vykreslil modrý a červený histogram dvou nejextrémnějších. Vidíte, že o skutečném rozdělení nepodávají zrovna přesný obraz - a to padesát bodíků není zas tak málo (v sekci Jauvajs se dnes lehce zmíním o testování hypotéz, které se mimo jiné zabývá právě problémem, zda daná data pocházejí z předpokládaného rozdělení).
Realita dokáže být ošidná a nikdy nevíte, jak daleko je váš konkretní soubor vědomostí a zkušeností od skutečnosti. Proto se vyplatí pozorovat, číst, srovnávat, naslouchat druhým. Dát hlavy dohromady, tam kde to jde, aby náš odhad byl v dané situaci co nejpřesnější.
Z téhož důvodu nemá smysl v internetových diskusích „argumentovat příkladem“. I kdybyste znali sebelepší soukromou školu v Yorkshire, neříká to o srovnání českého a britského vzdělávacího systému vůbec nic. Je to jen jeden datový bodík. Udělat z něho jakýkoliv závěr, by bylo stejně nepřesvědčivé jako tvrdit, že ženy jsou vyšší než muži, protože vaše vytáhlá sousedka hraje basket a je nejvyšší v baráku.
Naštěstí máme mechanismus, jak svá osobní pozorování kombinovat s ostatními členy dané komunity. V politice jsou to svobodné volby, v ekonomice volný trh. V nich se individuální dojmy posčítají, odchylky napravo a nalevo se vyruší a to co dostaneme, bude solidní obraz reality. Někdo si myslí, že cena akcií Microsoftu by měla být vyšší, někdo si myslí, že by měla být nižší. Trh si nemyslí nic - jen si všechny osobní postřehy hezky ováží a vydá svůj verdikt. Jedinec tu komplexitu vzájemně propletených vstupů a výstupů ve své hlavě neukočíruje.
Navíc v diskusi nemůžete prostě odrecitovat kompletní histogram svých zkušeností. Na to není rétorika vybavena (debata by pak vypadala jako zpráva o stavu vody na českých tocích). V daném kontextu se musíte verbálně postavit na tu či onu pozici. Kapitalista je hodný. Kapitalista je zlý. Asi nejlépe to vystihl Malý princ: „Řeč je pramenem nedorozumění.“
V jistém smyslu ta nutnost vyslovit v diskusi konkrétní soud připomíná kolaps vlnové funkce z kvantové mechaniky. Částice si spokojeně žije ve svém pravděpodobnostním světě, včetně možnosti být trochu tady a trochu tamhle - stejně jako kapitalista, který je trochu zlý a trochu hodný. Ale jak na ni dopadne kladivo měření, musí si vybrat. A možná i proto si nerozumíme. Kdybychom mohli porovnat své zkušenostní histogramy, asi bychom zjistili, že se až tak moc neliší. Jenže my je musíme zredukovat do jedné srozumitelné věty.
Proč se finále play off nehraje jen na jeden zápas
Protože náš svět je mnohovrstevnatý a zapeklitě propojený, o úspěchu často rozhoduje statistická výslednice složitého labyrintu souběžných procesů.
Hezky je to vidět ve sportu. Některé týmy jsou lepší, některé horší, ale tu a tam, když pámbů dopustí, i horší tým si na ten lepší může vyšlápnout (viz pohárová vítězství celků z nižších tříd). Faktorů je ve hře dostatek: silnější slabého podcení, klíčový útočník se nachladí, obránci se narodila dcera a trochu oslavoval, v kabině je dusno, rozbahněný trávník nahraje méně technickému, ale urputnějšímu soupeři - a to jmenuji jen ty poctivé (o tom, že nějaká sketa podplatila rozhodčího, pomlčím).
Zkrátka kdyby se play off hrálo na jeden zápas, byla by to takřka loterie. V jednom utkání se může stát cokoliv - míč je kulatý a fotbal nemá logiku. Když těch zápasů ale sehrajete víc, kvalita lepšího týmu se projeví - a čím víc zápasů se odehraje, tím má větší šanci vyplavat na povrch.
Abychom se mohli podívat, jak ta kvalita prosakuje do výsledků, postavíme proti sobě dva modelové týmy, kterým budu říkat Hradec a Sparta (a aby si jindřichohradečtí nedělali plané naděje, na mysli mám samozřejmě Votroky). Každý tým - jak fotbaloví fanoušci vědí - občas podá průměrný výkon, tu a tam nadprůměrný a výjimečně i výjimečný. Průměrný výkon si označíme hodnotou 100 a pro každý tým si vygenerujeme rozdělení s tím, že kvalitnější tým (Sparta) bude mít to rozdělení posunuté trochu doprava (protože pro něj jsou nadprůměrné výkony o něco pravděpodobnější).
Rozdíl kvality obou týmů bude dán rozdílem středních hodnot obou rozdělení (což si můžeme zhruba představit jako vzdálenost R, o kterou je „vrcholek“ lepšího rozdělení posunut doprava). Momentálně je Hradec ve 2. lize, takže na obrázku je to posunutí kvality celkem markantní (R = 10).
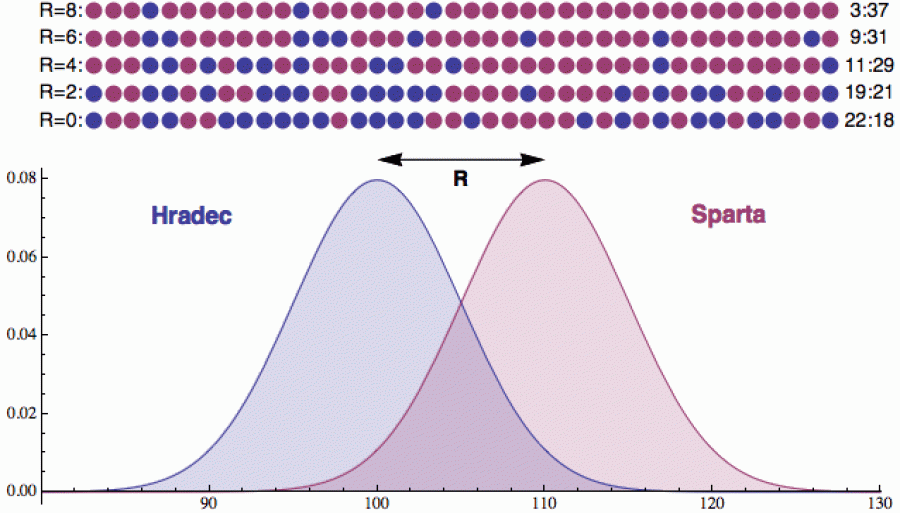
A teď si můžeme začít generovat „syntetická“ utkání, kdy si před
každým zápasem z daných rozdělení vygenerujeme kvalitu výkonu obou týmů a ten, kdo si „vytáhne“ vyšší číslo, vyhraje (kolečko nad grafem
pak bude obarveno příslušnou barvou). Pochopitelně, čím je R větší, tím je pravděpodobnější, že vyhraje lepší tým (neb si
„vytáhnul“ lepší výkon).
Nad obrázkem jsem vynesl statistiku 40 syntetických zápasů pro různé hodnoty R (výsledné skóre série je vpravo za každým řádkem). Vidíte, že pro R = 0 (stejná rozdělení) je to prakticky loterie. Jak se R zvyšuje, Sparta začíná vyhrávat častěji a častěji. Všimněte si ale, že i pro R = 6 se v řádku objevily tři hradecké výhry za sebou. Je to stále náhodný proces a při generaci výsledků můžete dosáhnout i nečekaných konfigurací (ale budou poměrně vzácné).
Play off se obvykle hraje na 4 vítězné zápasy. Ani to nemusí být samo o sobě garantem, že zvítězí lepší tým - obzvlášť pokud jsou síly vyrovnané (na řádku R = 2 má o trochu slabší Hradec stále ještě sérii pěti výher v řadě). Ale občas musí člověk (či pořadatel) přistoupit na kompromis mezi přesností a praktičností. Zvýšení na 5 vítězných už by asi fanoušky psychicky odrovnalo.
Většinu hodnocení je tedy třeba chápat statisticky. Řeknu-li, že Sparta je lepší než Hradec, neznamená to, že by musela vyhrát každý vzájemný souboj. Stejně tak tvrzení, že muži jsou vyšší než ženy, neznamená, že náhodně vybraný muž bude vyšší než náhodně vybraná žena. Proto používáme kouzelné slůvko „v průměru“. Pokud vám někdo bude tvrdit, že černoši hrají basket lépe než běloši, nemá smysl mu oponovat tím, že znáte jednoho kluka, co hraje za RH Pardubice jako bůh. Statistický výrok můžete nahlodat jedině tím, že přinesete nějakou uvěřitelnou statistiku v opačném gardu.
Proč je imigrační diskuse tak obtížná
Politická scéna se polarizuje a významnou měrou tomu přispívá i imigrační téma. Jako každý netriviální problém má celou řadu faktorů, příčin a aspektů. V této sekci se soustředím na jeden, který má statistický podklad.
Cílem každého člověka je prosadit se. Nejen jako jednotlivec, ale i jako skupina - ať už je to rodina, obec či celý národ. V předchozí sekci jsme viděli, že úspěch kolektivu má v podstatě statistický charakter. A to platí i v hospodářství. Aby byla společnost úspěšná, potřebuje mít co nejvíce jedinců s kladnými vlastnostmi a co nejméně se zápornými.
Když jsem o imigrační otázce mluvil se známými v Čechách, na prvním místě byla skoro vždy obava, jak se masový přísun imigrantů do Evropy projeví na celkových statistikách společnosti - tedy na ukazatelích, které rozhodují o kolektivním úspěchu či neúspěchu. A to jak v aspektech pozitivních (pracovitost, talent, charakter), tak v aspektech negativních (kriminalita, podvody, nevychovanost).
V každé lidské skupině existují problémy. Nemakačenky nebo přímo padouchy najdeme po celém světě. Otázkou je v jaké míře. V každé populaci se občas narodí šílenec, který popadne flintu a vystřílí celou hospodu. Stejně tak budou určitou část společnosti tvořit líní lemplové. S tím nic nenaděláme. Nad genetickou loterií nemáme kontrolu. U ekonomické imigrace ale kontrolu máme - nejsme povinni přijmout každého (tedy teoreticky).
Protože i každý národ chce uspět, při imigraci si tedy přirozeně vybírá ty, kteří v něm (statisticky vzato) posílí pozitivní vlastnosti a oslabí ty negativní. Je to trochu jako když do méně koncentrovaného džusu přiléváte více koncentrovaný. Jeho kvalita bude stoupat. Proto je jedno, že někdo viděl z rychlíku notorického flákače se syrským pasem a někdo jiný zase šikovného syrského inženýra. Jednotlivosti nehrají roli. Důležité jsou koncentrace (tedy procenta). Je mezi imigranty potenciálních pracantů méně, nebo více než ve stávající populaci? Nebo jsou ta rozdělení plus minus stejná?
K tomu abychom tuto otázku mohli posoudit, potřebujeme znát relevantní statistiky. Sestavit z omezených dat věrný obrázek reality vůbec není jednoduché (jak jsme viděli výše). Abych zrádnost takového přístupu ilustroval, modifikoval jsem ten experiment z politické sekce pro výběr dat ze dvou podobných rozdělení.
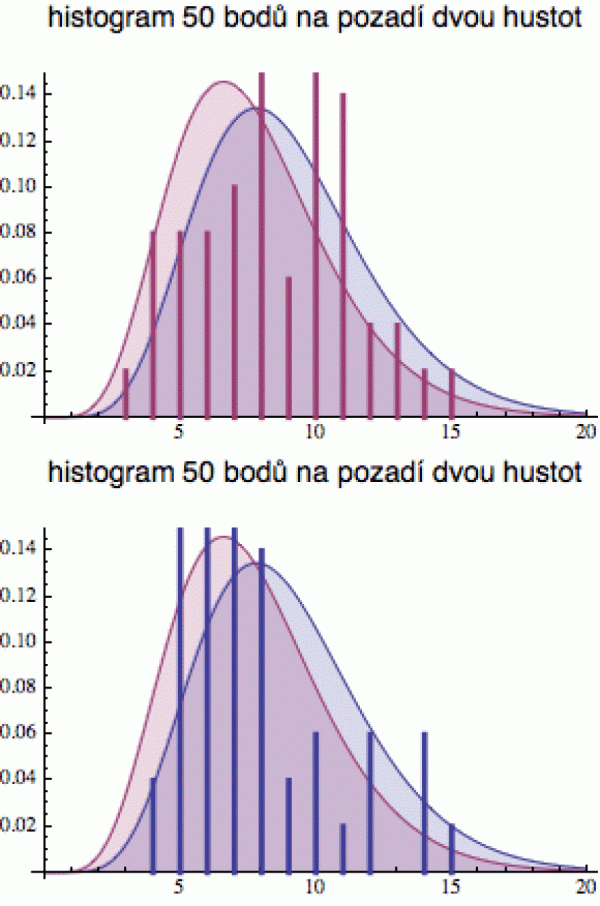
Představme si, že stávající společnost je reprezentována červeným rozdělením a ta příchozí modrým (a schválně nebudu říkat, zda sleduji pozitivní, nebo negativní vlastnosti - abych nerozpoutal lítou politickou přestřelku).
Vygeneroval jsem deset kolekcí dat z modrého i červeného rozdělení a na obrázku vám ukazuji ta data, která vykázala největší posun směrem k „druhému“ rozdělení. Vidíte, že i pro 50 bodíků se vám může lehce stát, že data z červeného rozdělení (červené úsečky) spíš připomínají to modré a naopak. Jinými slovy, pokud se omezíte jen na pár osobních zkušeností, není snadné poznat, ze kterého rozdělení data pocházejí - realita se vám může jevit velmi zkresleně (pro 500 bodíků už by se takové „obrácení“ asi nepovedlo).
Každý vidíme trochu jiný výsek skutečnosti a bez solidních statistik nebude snadné debatu nějak uzavřít. Tím spíš, že politická opatření v této oblasti jsou jen těžko zvratitelná. Když zvýšíte daně a ukáže se, že jste tím ochromili ekonomiku, daně se sníží a jede se dál. Pokud ale výrazně změníte statistický charakter evropské populace, napravovat se to bude jen velmi těžko.
EU by tedy měla mít eminentní zájem takové statistiky veřejnosti poskytnout. To je ale těžký statistický oříšek, jednak proto že dvě populace pocházející ze zcela rozdílných podmínek se těžko srovnávají, a jednak je to horký politický brambor, protože kdykoliv se objeví snaha dvě takové populace statisticky porovnat, skoro vždy se vzedme vlna vášní, která zcela pohltí jakoukoliv racionální diskusi.
Existuje ještě jeden důvod, proč je imigrační debata obtížná.
V poslední době mám při pročítání diskusí pocit (a u polarizovaných témat to platí dvojnásob), že není důležité zúčastnit se, ale zvítězit. Jakkoliv.
 Představme si škálu názorů jako plus minus
normální rozdělení (obrázek vpravo), kde v levém extrému najdeme
vyholené lebky skandující „ať táhnou nazpátek“, zatímco v pravém
cípu se pod transparentem „přijďte všichni do Evropy, místa je dost“
srotili vyšinutí sociální inženýři. Každý z nás máme v tom
rozdělení své místo. Většina (doufejme) někde uprostřed.
Představme si škálu názorů jako plus minus
normální rozdělení (obrázek vpravo), kde v levém extrému najdeme
vyholené lebky skandující „ať táhnou nazpátek“, zatímco v pravém
cípu se pod transparentem „přijďte všichni do Evropy, místa je dost“
srotili vyšinutí sociální inženýři. Každý z nás máme v tom
rozdělení své místo. Většina (doufejme) někde uprostřed.
Pokud chcete argumentačně vyhrát, nejlepší strategií je promlouvat k nejodlehlejšímu táboru soupeře. Pak se kontrast mezi vaším umírněným názorem a extrémní (ergo chybnou) pozicí z opačného pólu projeví nejzřetelněji. A tak se rozumní (červení) vítači ostře vymezují proti radikálním (modrým) odmítačům a naopak. V debatě pak místo konstruktivních návrhů poletují nesmyslné rasové invektivy o barvě kůže, která sama o sobě prakticky nikomu nevadí.
Diskuse umírněných s umírněnými (červená část spektra) by možná neměla svého vítěze, ale mohla by se poměrně rychle dobrat přijatelného kompromisu.
Proč mají Němci lepší fotbalový tým než Češi
V minulých sekcích jsme viděli, že úspěch má statistický charakter - ať už se jedná o národní ekonomiku nebo o sportovní tým. Ten, kdo má kvalitnější rozdělení, je na koni.
O jednom aspektu jsem se ale zatím nezmínil. Pokud jsou obě rozdělení stejná, pak výhodu má ten, kdo si z nich může nabrnkat bohatší datový soubor (tedy více čísel). To je intuitivně jasné. Ten, kdo má možnost si z osudí (při stejném rozdělení) vytáhnout víc hodnot, má samozřejmě větší šanci, že mezi nimi objeví pár extrémů (v tomto případě mimořádně talentovaných fotbalistů). Jinými slovy, kdo si koupí víc loterijních lístků, má větší šanci na výhru.
Abychom viděli, jak to konkretně funguje, uděláme si opět malý experiment. Vezmu si to „hradecké“ fotbalové rozdělení (tedy normální s průměrem 100 a odchylkou 5) a vyberu si z něho dvě poměrně rozsáhlé datové sady, reprezentující fotbalové populace - větší německou (DE) a menší českou (CZ). A z každé sady vám ukážu nejlepší jedenáctku (tedy 11 nejvyšších čísel).
Nejprve TOP11 pro 10 000 čísel za CZ data a 20 000 za DE.
CZ: 118.0, 117.9, 117.8, 116.8, 116.7, 116.5, 116.4, 116.3, 116.0, 115.9,
115.6
DE: 119.7, 117.5, 117.4, 117.4, 117.3, 117.2, 117.0, 116.6, 116.4, 116.4,
116.4
Vidíte, že už v tomto případě mají Němci tu jedenáctku kvalitnější, i když 6 nejlepších Čechů by se do ní ještě vešlo (a opět připomínám, že těch 10, resp. 20 tisíc čísel jsem vybral ze stejného rozdělení). Tato verze ovšem neodráží realitu. Němců není dvakrát tolik, ale osmkrát. Takže ještě jeden příklad, kdy vytáhnu za českou stranu z „hradeckého“ rozdělení dalších 10 000 čísel a za německou 80 000. Zde jsou nejlepší jedenáctky:
CZ: 118.3, 117.7, 117.5, 117.5, 117.5, 116.5, 116.4, 116.2, 116.1, 116.0,
115.8
DE: 121.2, 119.8, 119.7, 119.2, 119.2, 119.1, 119.0, 118.8, 118.6, 118.2,
118.1
Tady už se výhoda většího výběru projevila v plné síle - z Česka by se do německé reprezentace probojoval pouze ten první. Zbytek ani ťuk.
Každý člověk je v podstatě náhodnou směsicí talentů a dovedností, takže více lidí v dané zemi rovná se více hrábnutí do osudí s těmito talenty. Proto mají lidnaté země na olympiádách a šampionátech obecně nejvíc medailí.
Tím samozřejmě netvrdím, že fotbalová úspěšnost je přímo úměrná lidnatosti. Kdyby to platilo, tak by mistrovství světa vyhrávala Čína a malé Chorvatsko by se ani nekvalifikovalo.
V reálu je ve hře i spousta jiných faktorů. Například jak země se svými talenty zacházejí, určuje kvalitu rozdělení - jako v tom příkladu Sparta-Hradec (osobně si myslím, že Němci si nejen vybírají z populace vícekrát, ale mají i lepší rozdělení). A v neposlední řadě se hodí i kousek obyčejného štěstíčka. V předchozí sekci jsme viděli, že jednou za čas se i z horšího rozdělení dá vybrat kvalitní soubor dat.
Sečteno a podtrženo: sportovní úspěch je v podstatě kombinací velikosti datového souboru (populace), kvality rozdělení (úrovně sportovní infrastruktury) a přízně štěstěny.
Sekce jauvajs: Testování hypotéz
jen pro mimořádně otrlé povahy
Velmi často se ve statistice stává, že potřebujeme ověřit, zda dané datové soubory pocházejí z toho či onoho rozdělení nebo z rozdělení s určitými vlastnostmi. Tímto problémem se zabývá testování hypotéz (takových testů existuje dost na umoření osla a poměrně solidní výčet naleznete zde).
Většina testů se nějakým způsobem pokouší odhadnout pravděpodobnost, že obdržená data podporují testovanou hypotézu (např. že dva vzorky pocházejí ze stejného rozdělení). Protože ale rozdělení různých se vzorky spjatých veličin (např. rozdíl průměrů) se obecně řídí jiným rozdělením než proměnné samy o sobě, setkáte se v testech se spoustou exotických pravděpodobnostních hustot, např. chí kvadrát či Studentovo t-rozdělení.
Protože tato rozdělení závisejí na tom, jak velký vzorek (či vzorky) testujete, budete při jejich aplikaci potřebovat jeden důležitý údaj, a to počet stupňů volnosti), což je zhruba řečeno velikost vzorku (minus počet vázajících podmínek). Většina statistických kuchařek vám poradí, jak tuto kvantitu z naměřených dat spočítat. Anebo to za vás udělá přímo statistický software.
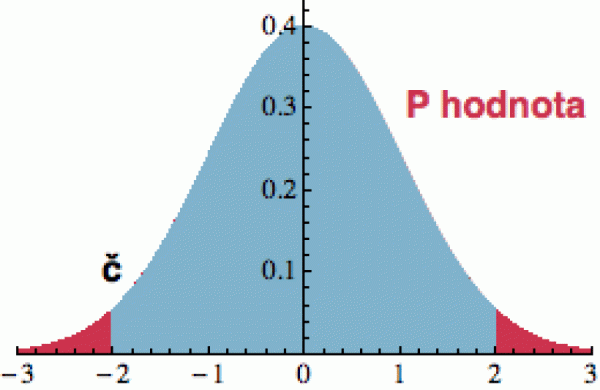
Nejprve jednoduchý příklad. Chcete otestovat, zda má nějaká normální populace průměr 0. Vezmete si vzorek, řekněme, dvaceti čísel a vyjde vám číslo č = -2. Je to hodně, nebo málo? Je jasné, že nemůžeme čekat, že nám vyjde přesně 0.0, ale -2 už se zdá hodně z ruky. Jak to tedy rozhodnout?
Minule jsme viděli, že i rozdělení vzorků má gaussovský tvar, jen je trochu užší. Z jeho znalosti tedy můžeme spočítat, jaká je šance, že bychom si vytáhli vzorek s průměrem -2 (nebo horším). Ta pravděpodobnost je na obrázku vyznačena červeně a říká se jí p-hodnota. Je to zhruba pravděpodobnost, že sledovaná veličina č nabývá naměřenou (nebo horší) hodnotu za předpokladu platnosti testované hypotézy (pro podrobnější diskusi nahlédněte sem).
Čím je ploška menší, tím je napočítané č nepravděpodobnější a to na naši hypotézu vrhá pochybnost (u většiny statistických testů je to číslo č o něco komplikovanější než jen průměr vzorku, ale princip je stejný). Občas nás zajímá pouze výchylka na jednu stranu, tzv. jednostranná hypotéza (one-tail), a pak prostě uvažujeme pouze jeden z obou naznačených extrémních ocásků. Na obrázku je ovšem testována hypotéza oboustranná (two tail).
Podívejme se na složitější příklad. Máme dva naměřené soubory s n = 5 hodnotami (např. váhy nějakých součástek vyrobených na dvou různých linkách) a chceme vědět, zda tato data pocházejí z rozdělení se stejnou střední hodnotou (tedy zda jsou obě linky stejně seřízené).
data1 = {23.26, 23.27, 23.19, 23.11, 23.14}
data2 = {23.16, 22.95, 22.93, 23.03, 23.02}
Všimněte si, že baj voko není jasné, zda tyto dva vzorky pocházejí z rozdělení se stejnou střední hodnotou - museli bychom si spočítat jejich průměry a rozptyly, a pak se snažit nějak posoudit, zda je rozdíl průměrů dostatečně malý (vzhledem k rozptylu). To je ovšem trochu subjektivní kritérium. Pro někoho by ten rozdíl mohl být snesitelný, pro jiného ne. Smyslem statistického testu je tento subjektivní pocit vyfiltrovat a přijmout nějaký standardní systém, jak platnost hypotézy rozhodnout.
V této konkretní situaci můžeme použít jednodušší verzi tzv. Studentova t-testu, ve které bude bude roli čísla č hrát normalizovaný rozdíl:
t = (p1 - p2) / s
kde p1 a p2 jsou průměry našich dat (n = 5) a s je zprůměrovaná odchylka, kterou dostaneme z rozptylů obou souborů podle vzorečku:
s = sqrt((s1+s2)/n)
Pro naše data vyjde:
p1 = 23.194
p2 = 23.018
s = 0.05138
a odtud dostaneme hodnotu t pro Studentův t-test
t = 3.4254
Tuto hodnotu dosadíme do Studentova kalkulátoru s df = 8 stupni volnosti a pro dvoustrannou (two-tailed) hypotézu obdržíme:
p = 0.009
A to je velmi málo. Pokud použijeme klasickou toleranci 0.05, musíme hypotézu zavrhnout (pokud by platila, takto naměřená data by se realizovala pouze v 0.9 % případů a to je méně než 5 %, které bychom byli ochotni skousnout).
Mimochodem, kdybychom chtěli testovat, zda vzorky pocházejí přímo ze stejného rozdělení, museli bychom použít ještě komplikovanější test (Kolmogorov-Smirnov).
Článek je redakčně upravenou verzí blogového příspěvku na serveru
iDNES.cz. Publikováno s laskavým svolením autora.
Další díly a původní texty jsou dostupné na blogu Jana Řeháčka.




