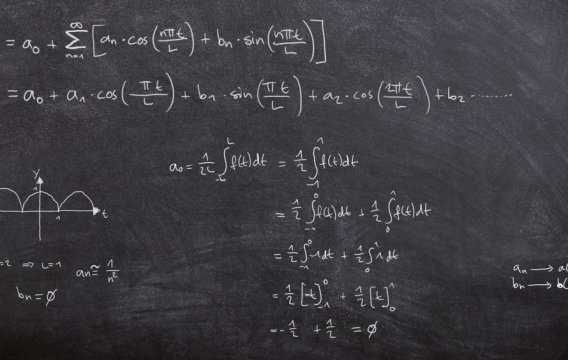Mezi studenty je jedním z nejoblíbenějších statistických procesů tzv. náhodná chůze, které se pro její zcela chaotický až motavý charakter říká též „opilcova procházka“. Tak si vytáhněte pár lahváčů z ledničky a půl je hotovo.
Statistika nepatří k disciplínám, které by naplnily roztěkanou mysl studentovu radostným očekáváním. Proto si bodrá chasa v podkatedří nenechá uniknout jedinou příležitost ke zpestření plavby sargasovým mořem vzorečků nějakou tou směrodatnou odchylkou od stanoveného kursu (před lety mi například jedna studentka přinesla do hodiny fretku, takže jsme asi dvacet minut místo lineární regrese naháněli po učebně šelmu lasicovitou). Není proto divu, že vyhaslé oči postpuberťáků vzplanou nelíčeným enthusiasmem, když se líný tok definic a teorém dokolébá k problematice opilcovy chůze. To se nad spálenou prérií zničehonic zazelená les zdvižených rukou:
„Prosím, prosím, a budou k tomuto tématu nějaká
praktika?“
„Já bych mohl u strýce z velkoobchodu obstarat koňak se
slevou!“
„Jestli budeme dýchat do balonku, tak já bych zapisovala
hodnoty.“
„Mohli bychom namísto do posluchárny B2 přijít rovnou do
hospody?“
„Já znám jednoho notorika - on by za láhev whiskey přišel na
besedu.“
Nuže, pro dnešek si během výkladu můžete trochu přihnout (jednu dvanáctku na každých třicet kilo váhy), ale pod podmínkou, že po vás v diskusi nezůstanou žádné nedopité flašky. A v sobotu se na nejbližším tankodromu klidně odvažte a zkuste si, jak daleko se v čase T a ve stavu podroušeném P dopotácíte vy.
Mimochodem, jedním z nejhezčích cestovatelských zážitků je procházka po lodi na rozbouřeném moři, protože se s vámi svět houpá jako po bečce rumu, ale přitom jste dokonale při smyslech, takže si tu opileckou perspektivu můžete patřičně užít.
Než se ale dostaneme k omamným uhlovodíkům, podíváme se na pár dalších detailů ze života náhodných proměnných. Kdo ví, co je rozptyl a střední hodnota (a tím myslím, kdo to ví za střízliva - po pěti panácích ovládá statistiku každý), může skočit rovnou na sekci Jauvajs.
Náhodné veličiny podruhé
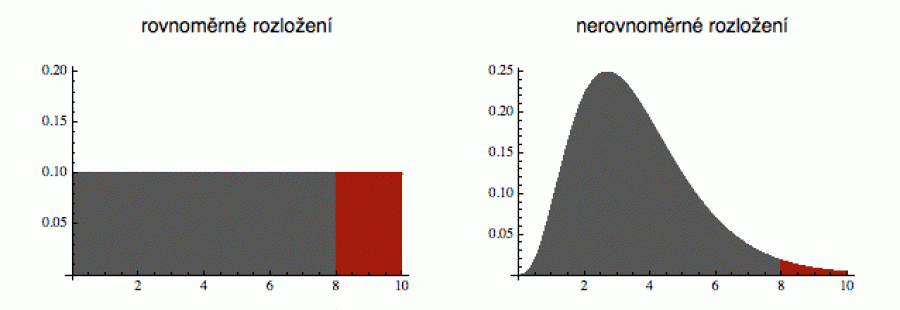
Když se řekne náhoda, normální smrtelník si představí otáčející se osudí loterie, v němž mají všechny pingpongové míčky stejnou šanci na vylosování. To znamená, že jejich rozdělení je zcela rovnoměrné (ve spojitém případě je definováno konstantní funkcí). Minule jsme ale viděli, že existují i náhodné veličiny, ve kterých se nahodilost snoubí s nějakou strukturou. Jejich pravděpodobnostní funkce (hustota) je pak nekonstantní a to umožňuje vyvoleným hodnotám x pronikat do měřených či odebíraných vzorků častěji než ostatním (viz obrázek).
(v obou případech je naznačená plocha rovna 1)
Graf napravo si můžete představit třeba jako délku služebního hovoru v minutách. Většinou to zmáknete za 2-4 minuty, ale občas vás někdo típne
dřív anebo se naopak pan šéf potřebuje vykecat, takže se dostane i na
jiné hodnoty. A to, že jsou limitovány jistými biologickými a vnitropodnikovými zákonitostmi, jim na nahodilosti neubírá. Délka
příštího hovoru se dopředu určit nedá.
Mimochodem, i v dynamických systémech jsme viděli, že chaotické nahodilé struktury nevznikají naráz mávnutím kouzelného proutku, ale postupně rozleptáváním deterministických orbit. Pokud bychom z polohy takového systému sestrojili náhodnou veličinu, pouze v extrémních případech by měla konstantní hustotu (tj. systém by se mohl nalézat v kterémkoliv bodě dané oblasti se stejnou pravděpodobností). Většinou by se v ní daly najít zbytky starého řádu.
Z pohledu matematiky je vcelku jedno, zda je pravděpodobnostní hustota konstantní nebo ne. V praxi to znamená pouze výpočetní výhodu. Když se mne zeptáte, jaká je pravděpodobnost, že náhodná veličina nahoře vlevo bude mezi 8 a 10 (to je ta část vyznačená červeně), vidím hned, že to je 0.2 (slovy dvacet procent). Interval délky 2 je pětinou intervalu délky 10. U telefonní veličiny vpravo to bude o hodně méně, baj voko tak 2 %, ale na přesný výpočet bychom tu funkci museli integrovat. Zda mají obě křivky stejné právo reprezentovat náhodu, je otázka, kterou přenechám filosofům.
Protože u rovnoměrného rozdělení mají všechna čísla stejnou šanci na vytažení, nezbyde nám nic jiného, než si je vybírat náhodně. Z toho by se mohlo zdát, že nerovnoměrné rozdělení bude tahat nejprve čísla s vyšší hustotou a pak ta s nižší. To ale není pravda - ta veličina je stále naprosto náhodná. Začneme-li zkoumat ženské výšky, nemůžeme čekat, že první číslo, které si s tlukoucím srdcem zapíšeme do zápisníčku začínajícího statistika, bude 168 cm, což je momentální průměrná výška Češek. Klidně můžete hned na počátku narazit na hráčku basketu a máte 180 cm, jen to hvízdne. Bude to ale trochu méně pravděpodobné.
Protože tohle je poměrně důležitý bod, podíváme se na generátor náhodných čísel s daným rozdělením podrobněji. Minule jsem popsal, jak si ho můžete podomácku sestrojit, a dnes se podíváme, jak si lze jeho fungování představit bez zabíhání do technických detailů.
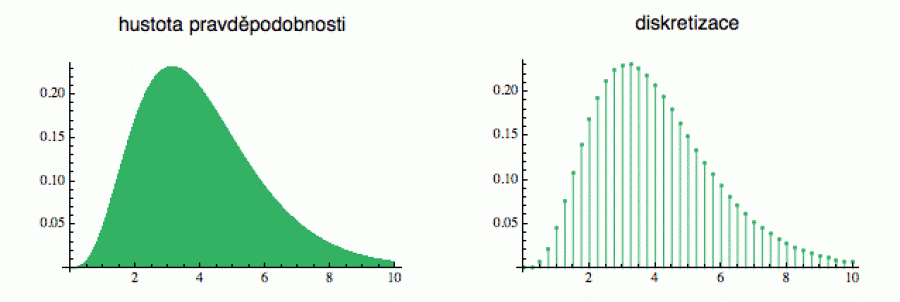
Nejprve hustotu náhodné proměnné diskretizujeme (tedy v podstatě
zaokrouhlíme), protože se spojitými veličinami se hůře pracuje. Tím
dostaneme namísto spojité křivky jakousi „sadu zelených tyčinek“
odpovídajících konkrétním hodnotám x (v mém
případě jsem vše zaokrouhlil na čtvrtiny celých čísel, ale můžete to
udělat i jemněji). Tyčinky pak nařežeme na tenká kolečka
(řekněme o tloušťce jeden milimetr) a na každé kolečko
napíšeme, jaké hodnotě x odpovídá (tedy z jaké
tyčinky pochází). Nakonec všechna dřevěná kolečka naházíme do
pytle, důkladně jím zatřepeme a pak je začneme s šátkem na očích
náhodně vytahovat. Takto generátor funguje.
Tam kde je hustotní funkce vyšší, je „zelená tyčinka“ delší, a tudíž je z ní více koleček, a tedy větší šance, že nějaké z nich z pytle vytáhneme. Pořád je to ale náhodné vytažení.
Kdyby šlo vyrobit generátor, který by dokázal postihnout nejen statistický charakter daného rozdělení, ale i konkrétní hodnoty, všichni statistici by byli milionáři, protože by si sestrojili dokonale věrný generátor loterijních čísel.
Tady máte pro ilustraci konkrétní příklad dvou datových sad, které jsem vygeneroval z těch prvních dvou rozdělení, rovnoměrného a nerovnoměrného.
(R) 7.9, 8.9, 3.2, 9.3, 9.8, 7.1, 4.3, 9.4, 0.4, 1.3, 0.9,
3.1, 4.1, 3.3, 3.4, 2.2, 2.3, 7.4, 6.7
(N) 3.6, 4.4, 4.9, 2.3, 3.5, 2.4, 5.6, 2.7, 3.1, 3.9, 9.5, 8.1,
2.2, 4.6, 1.8, 3.9, 5.0, 7.5, 4.0
Vidíte, že na první pohled se od sebe příliš neliší. Jsou to prostě dvě řady čísel vytáhnutých z klobouku, s hodnotami někde mezi 0 a 10. Přesto jsou jejich statistické vlastnosti odlišné, a pokud chcete generátor použít pro realistické modely, je potřeba věnovat důkladnou pozornost jeho rozdělení. Například pro modelování výšky žen by nám rovnoměrný generátor čísel mezi 150 a 190 cm prokázal medvědí službu.
A ještě vám ukážu celkem zajímavý a instruktivní příklad.
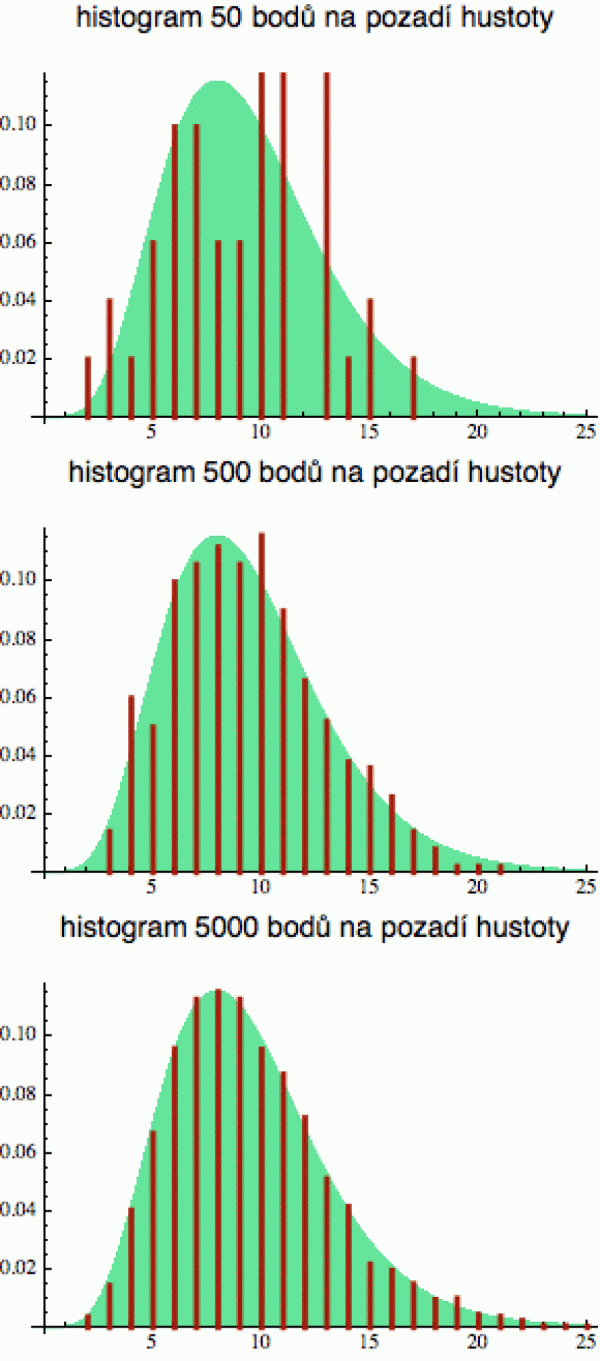
Vezmeme si opět jedno nerovnoměrné rozdělení a vygenerujeme si z něj 50
konkrétních hodnot. Ty zaokrouhlíme na celá čísla, sestrojíme z nich
histogram a normalizujeme ho (vydělíme příslušné četnosti 50),
abychom si takto obdržená data mohli vynést na grafu jako pravděpodobnosti.
Výsledek vidíte na obrázku vpravo (světle zelené pozadí reprezentuje
teoretické rozdělení naší veličiny, které jsem zadal do generátoru,
červeně je pak vykreslen normalizovaný histogram).
I když 50 konkrétních datových bodíků je celkem dost, vidíte, že statistika zde ještě pokulhává. Hodnota 8, kterou bychom teoreticky čekali nejčastěji, je v našem datovém souboru stěží zastoupená. Na druhé straně hodnota 13, v jejímž okolí je hustota už poměrně malá (takže by se v našem souboru moc vyskytovat neměla) se drze dělí o první místo.
Z prostředního obrázku vidíte, že teprve pro 500 bodíků se před námi začne zjevovat skutečný obraz naší náhodné proměnné. Úplně přesné to ještě není, ale základní rysy zelené křivky už jsou z toho „experimentálního histogramu“ vidět.
Když si zaznamenáte 5000 bodíků, ať už je naměříte nebo vygenerujete počítačem, dostanete velmi kvalitní aproximaci skutečného rozdělení. Tam už ten histogram „sedí“.
V praxi je to ovšem většinou tak, že zelené rozdělení neznáme a z naměřených dat ho odhadujeme.
Ale vraťme se ještě k hornímu obrázku. Možná si řeknete, že červený histogram by daleko lépe kopíroval nějaké jiné, řekněme růžové, pozadí se dvěma vyvýšeninami (a nehihnějte se tam vzadu, takovým rozdělením říkáme bimodální a v praxi se s nimi běžně setkáváme - např. při popisu hustoty dopravy, která má obvykle na časovém diagramu dva vrcholy - ranní špičku a odpolední). Bez znalosti dalších dat by se to ale jen těžko rozhodovalo. Vidíte, že zdání i ve statistice klame. Tímto problémem se zabývá tzv. testování hypotéz, které vám pro konkrétní data řekne, jaká je šance, že pochází z toho či onoho rozdělení.
A to nás dovedlo k velmi důležitému a praktickému ponaučení. To zelené rozdělení je v jistém smyslu kompletní popis daného problému, tak jak jej vidí - obrazně řečeno - pouze Bůh. My, pozemští smrtelníci, z té boží reality vždy vidíme jen konečný útržek - jakousi datovou aproximaci, kterou si vytváříme na základě našich zkušeností. A jak vidíte, ani 50 měření není dost na to, abychom vystihli skutečnou „povahu“ problému. To je důležité memento, které nás nabádá k ostražitosti a pokoře. Obzvláště u problémů socio-ekonomických, které mají velmi komplexní charakter a složitá rozdělení.
Přesto se v internetových diskusích občas vyskytují kabrňáci, kteří nemají problém realitu „kvalifikovaně“ ohodnotit už z 5 či 10 kousků dat (často vyčtených z pochybných zdrojů).
Průměr, medián a střední hodnota
Když na člověka spadne soubor dat (jako výše uvedené R a N), o jejichž rozdělení nemáme ani potuchy, první instinktivní reakce statistika je spočítat jejich průměr. Matematika teoreticky rozlišuje mezi průměrem aritmetickým, geometrickým a harmonickým, ale ve statistice si obvykle až na pár výjimek vystačíte s tím prvním. Tedy všechno sečíst a vydělit počtem průměrovaných čísel, tak jak jste se to naučili ve škole. Občas můžete n hodnotám hi přiřadit kladné váhy vi a pak dostanete tzv. vážený (aritmetický) průměr, který se spočítá podle vzorečku
P = (h1*v1+h2*v2+h3*v3+...+hn*vn) / (v1+v2+v3+...+vn)
(jsou-li všechny váhy vi = 1, pak
dostanete zpátky aritmetický průměr)
Celkem zajímavou alternativou aritmetického průměru je medián (tj. hodnota převládající "uprostřed" datového souboru). Získáme ho jednoduše tak, že data seřadíme podle velikosti a medián je pak hodnota přesně uprostřed takto vytvořené řady (pokud jsou uprostřed čísla dvě, což nastane, je-li dat sudý počet, vezmeme průměr těch dvou „prostředníčků“).
Na další řádce jsem uspořádal dvě datové řady vygenerované výše podle velikosti a červeně vyznačil jejich medián.
(R) 0.4, 0.9, 1.3, 2.2, 2.3, 3.1, 3.2, 3.3, 3.4, 4.1, 4.3, 6.7, 7.1, 7.4, 7.9, 8.9, 9.3, 9.4, 9.8
(N) 1.8, 2.2, 2.3, 2.4, 2.7, 3.1, 3.5, 3.6, 3.9, 3.9, 4.0, 4.4, 4.6, 4.9, 5.0, 5.6, 7.5, 8.1, 9.5
Pro srovnání, jejich aritmetický průměr je r = 5.002 a n = 4.360. To nerovnoměrné rozdělení má průměr i medián trochu nižší, protože když se podíváte na jeho tvar, je trochu „šoupnuté“ do nižších hodnot (ve srovnání s tím rovnoměrným).
Zatímco průměr ukazuje agregátní (naakumulovanou) hodnotu, rozpočítanou na všechny členy souboru, medián indikuje podmínky panující v jeho středu. A jako takový je nezávislý na změnách (klidně i extrémních) na obou koncích té uspořádané řady čísel (když to poslední číslo přepíšete na 10 nebo dokonce na 100, s mediánem to ani nehne - s průměrem ano). A to je v některých situacích žádoucí. Počítáte průměrný plat v nějaké vesničce a vyjde vám 12,000 Kč. Za rok se do ní přistěhuje excentrický milionář a hnedle je průměrný plat 20,000 Kč. Přitom ti zbylí obyvatelé jsou stále stejně chudí. Medián se tím milionářem ošálit nedá. I když poslední číslo v řadě vystoupá k nebetyčným hodnotám, to červeně zvýrazněné uprostřed bude stále stejné.
Nagenerovat si z nějaké náhodné veličiny soubor konkrétních dat a pak spočítat jejich průměr, je vcelku jednoduchá operace, ale má jednu výraznou vadu. Takový průměr závisí na konkrétní realizaci - tedy na vašem konkrétním datovém souboru. Pokud si změříte výšky 100 žen, dostanete jedno číslo. Pokud si druhý den změříte výšky jiných 100 žen, dostanete trochu jiné číslo.
Pokud ale znáte rozdělení příslušné náhodné veličiny - a to samozřejmě není vždycky - můžete si její „očekávaný“ průměr spočítat přímo z něho (rozdělení v sobě obsahuje všechny nezbytné ingredience). Této abstraktní kvantitě, nezávislé na konkrétní empirické realizaci, se říká „střední hodnota“ náhodné veličiny (anglicky expected value) a je to idealizovaný průměr všech dat, které by se z náhodné veličiny daly vyždímat (odteď až do skonání světa).
Také si ji ale můžete představit jako „vážený průměr“ všech možných hodnot x, kde „váhami“ jsou jejich pravděpodobnosti. Pokud se vaše náhodná proměnná skládá ze dvou hodnot a jedna z nich padá 4x častěji, bylo by fér dát jí v tom idealizovaném průměru čtyřnásobnou váhu (a obecně dát každé hodnotě váhu úměrnou její pravděpodobnosti).
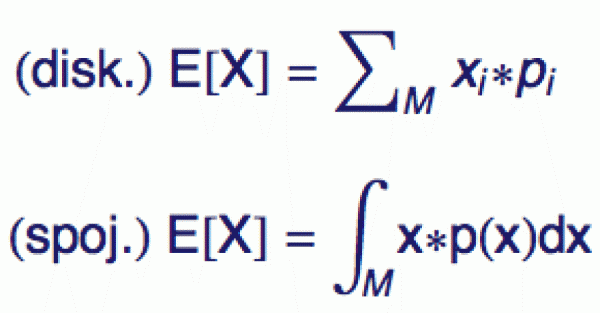
Pro diskrétní náhodné veličiny je tedy střední hodnota, tradičně
značená E[X], definovaná součtem vpravo. Pokud je náhodná veličina
rozdělena rovnoměrně, střední hodnota není nic jiného než aritmetický
průměr jejích N hodnot (všechny pravděpodobnosti jsou pak rovny
1/N). Ve spojitém případě se samozřejmě musí použít spojitý
součet (tedy integrál). Oba výrazy mají formálně stejnou
strukturu (symbol M znamená, že sčítáme či integrujeme přes všechny
možné hodnoty náhodné veličiny X) a v době statistických softwarů
je za vás pravděpodobně spočítá počítač. Důležitější je vědět,
co to číslo E[X] znamená. Když si začnete házet korunou a počítat
konkrétní četnosti orlů (vydělených počtem hodů), brzy
zjistíte, že toto číslo se blíží k teoreticky předpovězené
pravděpodobnosti orla, což je 0.5. Ve stejném smyslu se průměry hodnot
produkovaných náhodnou veličinou (ať už je to hod kostkou nebo nějaké
experimentální měření) začnou s rostoucím časem blížit její
střední hodnotě.
A na závěr sekce jednu malou aplikaci
Nabídnu vám následující hru: v klobouku mám dvě červené kuličky, tři modré a pět zelených. Pokud vytáhnu červenou kuličku, dám vám 200 Kč, pokud modrou, dám vám 300 Kč a pokud zelenou, dám vám 800 Kč. Ale protože tahání kuliček z klobouku je šílená dřina, za každé vytáhnutí mi zaplatíte 500 Kč. Berete?
Abyste mohli rozhodnout, zda se vám tato hra vyplatí, potřebujete zjistit, jak velkou odměnu můžete v průměru očekávat. Tedy potřebujete spočítat střední hodnotu (de facto průměrnou „výplatu“) náhodné veličiny X definované naší hrou.
Je to veličina diskrétní a má tyto hodnoty (a pravděpodobnosti):
200 (0.2)
300 (0.3)
800 (0.5)
To znamená, že podle vzorečku (disk.) dostaneme:
E[X] = 200*0.2 + 300*0.3 + 800*0.5 = 530
Střední hodnota obdržené sumy je tedy 530 Kč. A když odečtete 500 Kč za vytáhnutí kuličky z klobouku, stále vám v průměru zůstane 30 Kč.
V delším časovém horizontu ze mě tedy budete ždímat peníze (i když vám třeba úvodní hra nevyjde, pokud zrovna vytáhnu červenou kuličku). Statistika vám zaručuje bezpracný příjem. A to je jeden z důležitých významů střední hodnoty. Postihnout dlouhodobé chování náhodné veličiny (aritmetický průměr čísel 200, 300 a 800, což je bratru 433 Kč, by vám v tomto případě podal zavádějící informaci, protože neodráží fakt, že 800 padá daleko častěji).
Rozptyl a směrodatná odchylka
Průměr sám o sobě vám toho o datovém souboru (a potažmo o náhodné veličině, která ho vygenerovala) příliš mnoho neřekne. Ještě potřebujete vědět, jak moc se jednotlivá data od toho průměru liší. A tuto informaci poskytuje statistický ukazatel, kterému říkáme rozptyl.
Hmotnost lidí v linkovém autobuse se pasažér od pasažéra výrazně mění, protože služeb autobusové dopravy využívají lidé hubení i nehubení. Budete-li ale měřit hmotnost v plaveckém oddíle 8. B, zjistíte, že se jednotlivá data (hmotnosti) budou od průměru lišit poměrně málo, protože všichni jsou zhruba stejně staří sportovci a mají tudíž velmi podobnou hmotnost.
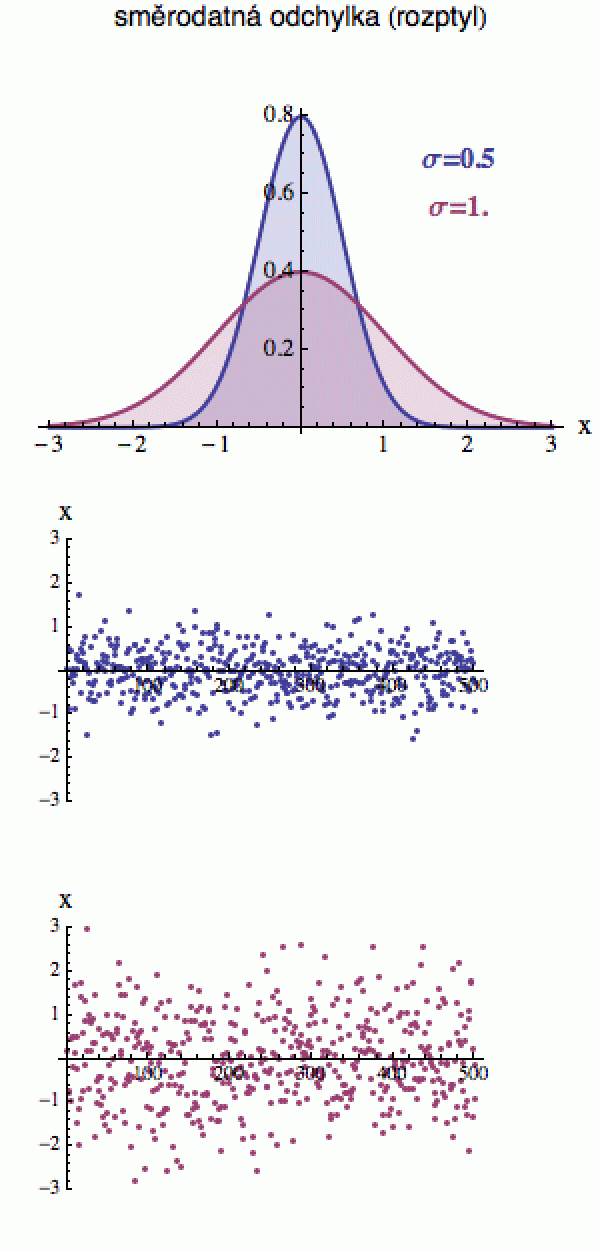
Podívejte se na dva datové soubory vpravo (každý čítá 500 kousků). V horní části obrázku máte vykreslena rozdělení, ze kterých jsem tato data
vygeneroval.
Oba datové soubory pod nimi mají střední hodnotu 0 (to znamená, že vykreslené bodíky oscilují kolem nuly), ale liší se rozptylem. Ten modrý soubor se od střední hodnoty příliš nevzdaluje a drží se zhruba v jednotkovém intervalu kolem ní, zatímco červený si lítá v podstatně širších mezích, cirka od -3 do 3.
Rozptyl toto chování jistým způsobem kvantifikuje. Čím je vyšší, tím je křivka pravděpodobnostní hustoty širší a to znamená, že vykreslené body se mohou více vzdálit od střední hodnoty.
V první aproximaci si rozptyl (přesněji směrodatnou odchylku, která je jeho odmocninou) můžete představit jako průměrnou vzdálenost datových bodů od střední hodnoty. Ty modré se od střední hodnoty 0 odchylují podstatně méně než ty červené, proto mají menší rozptyl.
Z pohledu náhodných proměnných je rozptyl σ2 definován jako střední hodnota rozdílu mezi aktuální hodnotou a střední hodnotou, tedy E[(X-μ)2], kde μ = E[X]. Ale to jen tak pro zasmání.
Rozptylové vzorečky pro jednotlivé náhodné proměnné jsou poměrně technická záležitost, plná zapařených sum a integrálů, takže na této úrovni si s nimi nebudeme lámat hlavu. Wikipedia vám většinou pro každé rozdělení prozradí, jaký je jeho průměr (mean) a rozptyl (variance).
Pro konkrétní datový vzorek x1, x2, ... xn s průměrem μ se ale rozptyl σ2 spočítá celkem jednoduše. Všimněte si, že sčítáme čtverce, aby se kladné a záporné odchylky nevyrušily (to by uměle snižovalo variabilitu vzorku):
σ2 = ((x1-μ)2 + (x2-μ)2 + ... (xn-μ)2) / (n-1)
(pokud vás zajímá, proč je ve jmenovateli (n-1), a ne n, mrkněte se sem)
Po odmocnění dostaneme z rozptylu i směrodatnou odchylku σ.
Na procvičení: data = (4,5,6,8,12) mají průměr 7, rozptyl σ2=10 a směrodatnou odchylku σ = sqrt(10) = 3.16.
Odchylka σ nám poskytuje přirozenou univerzální jednotku pro odhad, jak daleko je konkrétní x od průměru (či střední hodnoty) - jinak by se ty vzdálenosti pro náhodné proměnné, které se mohou řádově lišit, těžko porovnávaly. Čím vyšší sigma, tím dál se můžete od střední hodnoty vzdálit a zůstat při tom v nějakém rozumném rozmezí pravděpodobnosti. Hezky je to vidět u normálního rozdělení. Mezi μ-σ a μ+σ se vždy vejde zhruba 68 % všech hodnot x dané náhodné veličiny (na dalším obrázku tmavě zelená část), ať je to x samo o sobě v řádu jednotek, tisíců nebo miliard. To, co leží od průměru dál, než σ už je relativně nepravděpodobné (cca 1 ku 3) a šance, že se vzdálíte o víc než 2σ, už je velmi malá (cca 1 ku 20).
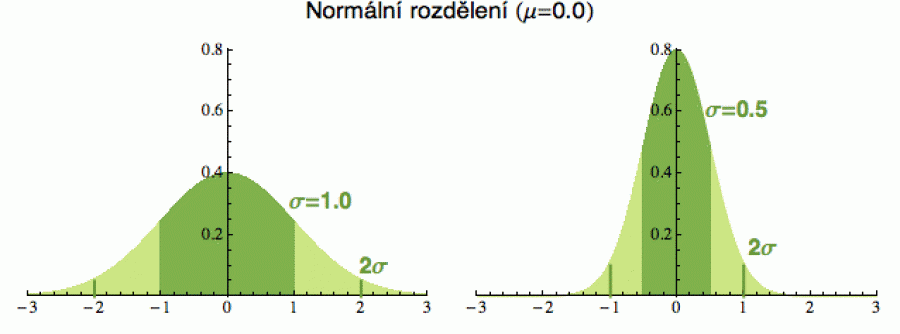
Zkušení praktici si ale s pravděpodobností moc hlavu nelámou a prostě to
σ používají jako obecně srozumitelnou jednotku „nepravděpodobnosti“.
Pokud naměříte x = 126, pro náhodnou proměnnou se střední hodnotou μ =
120 a odchylkou σ = 2, ve statistické hantýrce by se o takovém měření
mluvilo jako o události 3-sigma, protože 126-120 = 6 = 3σ (více o tom zde
nebo zde).
Pouze asi čtvrt procenta všech hodnot leží od průměrné hodnoty dál než
3σ, je to tedy vskutku událost
nepravděpodobná.
A pro otrlé povahy ještě jednu ilustraci z oboru testování hypotéz
Velmi často si z dané náhodné proměnné X odebíráme vzorky (výběry rozsahu N), počítáme jejich výběrové průměry a zajímá nás, co se z nich dá usoudit o povaze náhodné proměnné (popř. o nějaké širší populaci). Na to potřebujeme vědět, jaké je rozdělení těch průměrů, označme si ho X', respektive jak ho odvodit z původního rozdělení. To je ve statistice samostatná a důležitá kapitola a pro normální rozdělení (se kterým se setkáme nejčastěji) platí, že pokud má původní rozdělení X odchylku σ, bude mít výběrové rozdělení průměrů X' odchylku σ'=σ/sqrt(N) a stejnou střední hodnotu.
V „trpasličí verzi“ to vzorkové (výběrové) rozdělení X' funguje takto. Zabušíme na vzorkového trpaslíka, jehož vzorkovna odebírá N vzorků, načež trpaslík vyběhne ven, Nkrát zabuší na trpaslíka z původního rozdělení X a po obdržení N hodnot z nich spočítá průměr a toto číslo nám vyhodí na výstupu.
Naměřme si tedy nějaký vzorek o velikosti N = 100 s průměrem řekněme p = 42. Je realistické očekávat, že tento vzorek pochází z normálního rozdělení X se střední hodnotou μ = 40 a odchylkou σ = 10? Kdyby to 42 byla individuální hodnota (a ne průměr), bylo by to jakž takž v cajku. Odchýlili bychom se od střední hodnoty pouze o 2, což je méně než „průměrná odchylka“ σ = 10. To by se dalo skousnout.
Pro vzorek ale platí tvrdší kritéria. Příslušné rozdělení vzorkových průměrů X' (pro N = 100) bude mít stejnou střední hodnotu E[X'] = 40, ale daleko menší odchylku σ' = 10/sqrt(100) = 1. To znamená, že kdyby náš naměřený vzorek (s průměrem p = 42) pocházel z rozdělení X, tak by ten průměr ležel 2σ' nad střední hodnotou (rozdělení X') a byl by to tedy setsakramentsky vzácný exemplář (pouze 4.5 % hodnot je vzdáleno od střední hodnoty víc než 2 sigma). Takže to moc realistické není.
Důvod, proč mají vzorková (výběrová) rozdělení X' menší rozptyl než ta původní X, je nasnadě. Uvnitř vzorku se extrémní hodnoty náhodné proměnné vzájemně vyruší, protože obvykle leží na různých stranách od průměru. A čím je vzorek větší (vyšší N), tím je větší šance, že se tak stane.
Výběrový průměr z náhodných hodnot tedy obecně „vyšiluje“ o něco méně než hodnoty samy o sobě.
Sekce jauvajs: Opilcovo pozdní odpoledne
Náhodná procházka (angl. random walk) je typ náhodného procesu, ve kterém se pohybujete po diskrétní množině bodů, a to tak že v každém kroku si „hodíte mincí“, do kterého ze sousedních bodů se vypravíte.
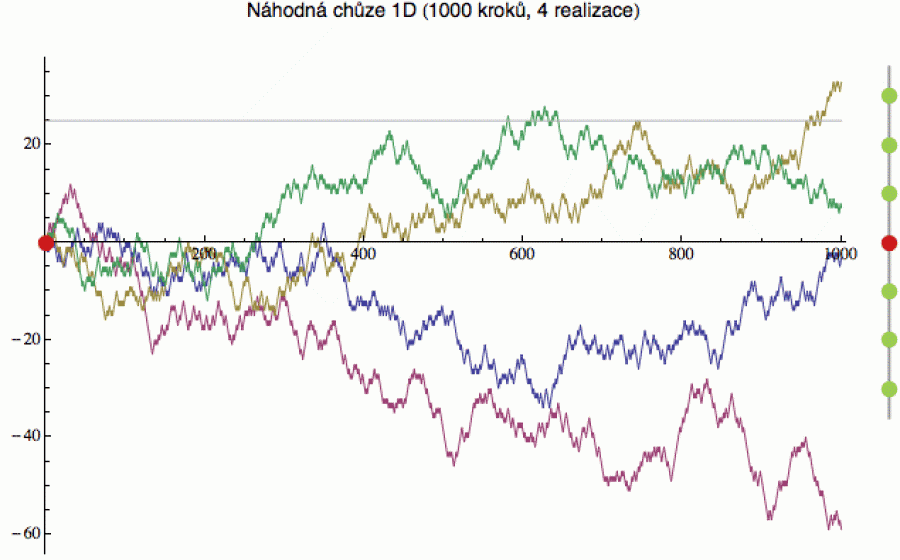
Nejjednodušší je to v jedné dimenzi (tedy na přímce). Na následujícím obrázku vpravo vidíte schematický náčrt situace. Na přímku rozmístíme nekonečně mnoho bodů (řekněme v celých číslech), postavíme se do „nuly“ a začneme procházku. Hodíme si mincí a padne-li nám orel, posuneme se o jeden bodík nahoru, padne-li panna, spustíme se o jeden bodík dolů. A tento proces neustále opakujeme.
Jak bude taková procházka vypadat po 1000 krocích, vidíte v levé části obrázku. Ta procházka pochopitelně není jednoznačná (protože si házíte mincí). Jinými slovy, když ji pro velký úspěch zopakujete - tedy postavíte se zpátky do nuly a opět začnete házet mincí - povede vás pravděpodobně úplně jinudy. Na obrázku jsem ji proto zopakoval celkem 4x (každá barva reprezentuje jednu náhodnou procházku).
Hráči rulety si často myslí, že černá a červená se střídají
víceméně pravidelně, a pokud bychom si vykreslili jejich průběžný
rozdíl, vznikla by z toho křivka bezbranně se šmrdlající v okolí nuly -
na to hřeší obzvláště gambleři, spoléhající na strategii zvanou
„martingale“ (tedy zdvojnásobení vkladu v případě
neúspěchu). Ten obrázek nahoře je ale právě takovou křivkou
(padne-li červená, posunete se o krok nahoru, pro černou o krok
dolů). A vidíte, že průběžný rozdíl četností obou barev se
dokáže od nuly poměrně dost vzdálit. Jak daleko se od ní v průměru
vzdálí, uvidíme za chvíli.
Aplikace náhodné procházky ale najdeme i mimo rámec hazardních her. Např. při návrhu průmyslových systémů musíte počítat s náhodnými perturbacemi, které systém posunují sem a tam. A někdy se stane, že se systém posune do nějaké kritické oblasti (na obrázku je vyznačena šedou čárou v úrovni y = 25), kdy dojde k selhání. Důležitou otázkou pak je, po kolika krocích se systém posune přes kritickou čárou (přesněji jaká je pravděpodobnost, že se přes ni přesune po N krocích).
Tento fenomén se někdy popisuje jako problém pádu z útesu. V úrovni y = 25 si představíme sráz a zajímá nás, kdy se k němu opilec dostane. Zelená trajektorie se k němu dostala už po cca 600 krocích, béžová o něco později a zbylé dvě se vydaly opačným směrem (do bezpečí). A protože je to proces náhodný, kdy jedna konkrétní realizace neznamená nic, opět nás zajímá hlavně to, jak často opilec z toho útesu „v průměru“ spadne (to si můžete poměrně snadno naprogramovat). Tyto problémy se někdy studují i pro „nesymetrické“ pravděpodobnosti, kdy se opilec potácne „nahoru“ s pravděpodobností p a dolů s pravděpodobností 1-p (více zde).
Další aplikace má náhodná procházka v modelování akciového trhu nebo ve statistické fyzice, při zkoumání Brownova pohybu. A komu ani to nestačí, může konsultovat tetičku Wiki.
Ve dvou dimenzích funguje opilcova procházka podobně. Opilec se pohybuje po čtverečkovaném papíře s tím, že začne uprostřed a v každém kroku si náhodně vybere, zda se dále vydá nahoru, dolů, doprava nebo doleva, včetně směru odkud přišel (i když existují typy náhodných procházek, kde je toto zapovězeno).
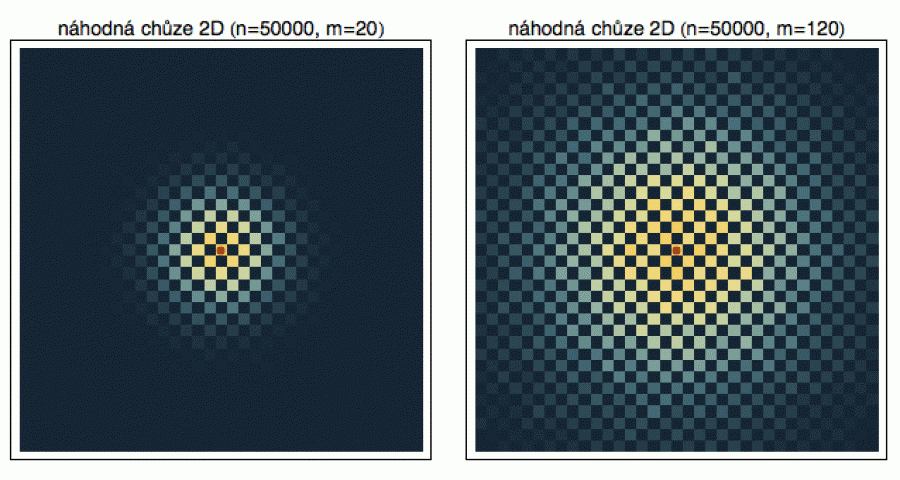
Dříve než se do 2D problému zakousneme, doporučuji tuto skvělou animaci. Nejprve si pomocí tlačítek X a Y navolte počet městských bloků a vyberte si, zda chcete rychlou (fast) nebo pomalou (slow) procházku. Pak si někde na vzniklé „mapě“ vyberte ťuknutím křižovatku, kde bude stát výchozí hospoda. Tlačítkem START pak zahájíte experiment a ťuknutím na QUIT ho ukončíte. Protože - stejně jako v 1D - se jedná o náhodný proces a dráha opilcova se bude v jednotlivých realizacích lišit, budeme se opět zajímat o statistiky. Tedy do kterých čtverečků se milé násosky dostanou častěji. Provedl jsem n realizací (vypustil z hospody n opilců) a zaznamenal si jejich polohu po m krocích. Pro každý čtvereček jsem pak spočítal, kolik opilců do něj dorazilo a vydělením n jsem získal pravděpodobnost „dobytí“ toho kterého čtverečku, podle níž jsem ho následně obarvil (jak pravděpodobnost stoupá, barva se mění od černé přes ocelově šedou až po žlutou - tam najdeme opilců nejvíc).
Z obrázku vidíte, že pro n = 200 opilců jsou výsledky ještě nedostačující. Intuitivně bychom čekali, že diagram bude symetrický - opilec má stejnou pravděpodobnost, dosáhnout čtverečky vlevo jako čtverečky vpravo. To je klasické úskalí statistiky (jak jsme to viděli už výše u histogramů na zeleném pozadí). Abyste dostali solidní obrázek, musíte mít dostatečně bohatá data. Pro n = 20000 opilců už diagram vypadá tak, jak očekáváme. Je symetrický a čtverečky blízko hospodě (červený startovní bod) jsou o něco pravděpodobnější než ty vzdálenější. Střední hodnota náhodné veličiny definované závěrečným čtverečkem naší dvacetikrokové chůze leží přirozeně v hospodě - kde jinde.
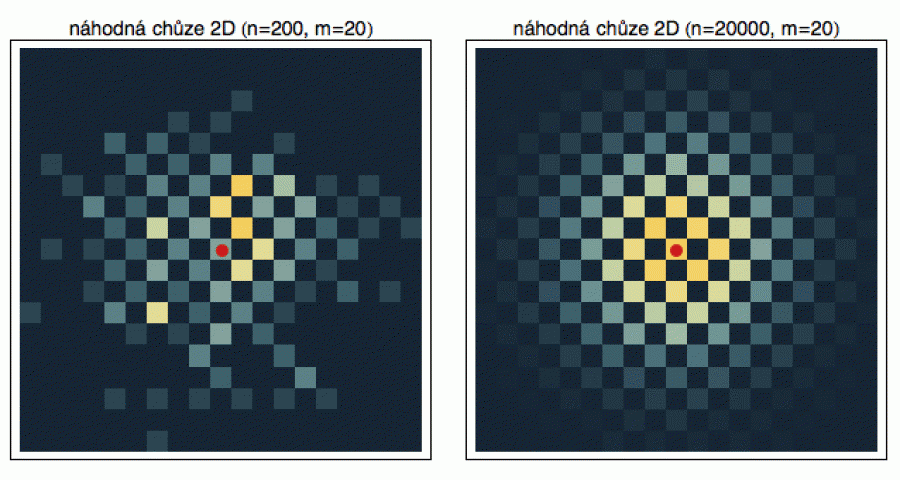
Možná si říkáte, proč ten obrázek vypadá jako šachovnice. Proč se
opilec nemůže dostat do čtverečku hned nalevo od hospody, kam by stačil
jeden úkrok doleva. To je proto, že jsme si zafixovali sudý počet kroků
m. Do toho čtverečku nalevo od hospody se dostanete po 1
kroku nebo po 3 (uděláte krok doleva, nahoru a dolů), ale nikdy se
do něho nedostanete po sudém počtu kroků. Pokud si chcete procvičit
mozkové závity, rozmyslete si proč. Stojí za tím parita (neboli sudolichost).
Označte si souřadnice čtverečků celými čísly (x,y) a uvědomte si, že
při každém kroku se parita součtu x + y mění.
Teď když víme, že pro solidní statistiky budeme potřebovat spoustu opilců, můžeme se podívat na jiný aspekt. Vezmeme si jich pro jistotu 50000 a necháme je bloudit m = 20 kroků (vlevo) a m = 120 kroků (vpravo). Barvy opět naznačují pravděpodobnost dosažení daného čtverečku po m krocích. Jak asi čekáte, rozptyl příslušné náhodné proměnné se zvětšil - více kroků znamená, že opilci se v průměru dostanou o něco dál od hospody. Otázka je, jak tato vzdálenost narůstá s počtem kroků.
Abychom na tuto otázku mohli odpovědět, vezmeme si n
opilců, necháme je udělat m kroků a změříme jejich
vzdálenost V od hospody (už nás tedy nebude zajímat,
kde přesně jsou, ale jen jak jsou daleko). A do grafu si pak pro každé
m vyneseme průměrnou vzdálenost V našeho
souboru n opilců od hospody. Pro n = 100
vidíte, že výsledek (modře) ještě dost kolísá, ale pro
n = 10000 už dostaneme poměrně stabilní křivku
(červenou), která vypadá trochu jako graf odmocniny. A nelineární
regrese skutečně ukáže, že tato křivka je (až na multiplikativní
konstantu) v podstatě odmocnina (diskuse zde).
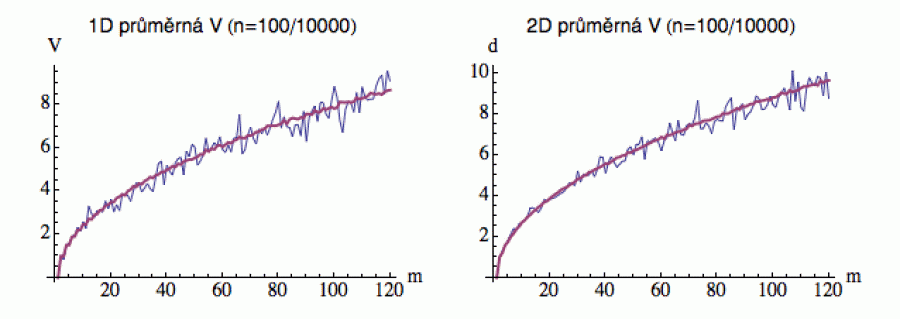
To znamená, že po m krocích se opilec v průměru dopotácí
do vzdálenosti sqrt(m). Oproti tomu střízlivý člověk,
který pokračuje stále ve stejném směru, se po m krocích
dostane do vzdálenosti m.
Takže si z dnešního Matykání pamatujte toto. Pokud vám záleží na rychlosti, nepijte. Chcete-li si ovšem dobře prohlédnout okolí, dejte si před procházkou frťana. Nebo dva.
Článek je redakčně upravenou verzí blogového příspěvku na serveru
iDNES.cz. Publikováno s laskavým svolením autora.
Další díly a původní texty jsou dostupné na blogu Jana Řeháčka.