Matykání XXXI: Jak vzniká chaos?

Kdysi dávno jsem v pracovně jednoho excentrického pana profesora objevil malý transparent s nápisem „Pořádek je pro blbce, inteligent zvládá chaos“. Dnes se podíváme, jak s tímto fenoménem zápasí samotná matička matematika.

Jednou z nejdůležitějších rolí matematiky - a speciálně dynamických systémů - je predikce. Pokud je pozorovaná veličina v tomto okamžiku tady, tak za rok by měla být plus minus támhle. A obvykle platí, že pokud poctivě změříme počáteční stav, dopídíme se konečného stavu s dostatečnou přesností. Výjimku tvoří tzv. chaotické systémy, které se dlouhodobé předpovědi úspěšně vzpouzí a chovají se - v souladu s Murphyho zákony - jak je zrovna napadne.

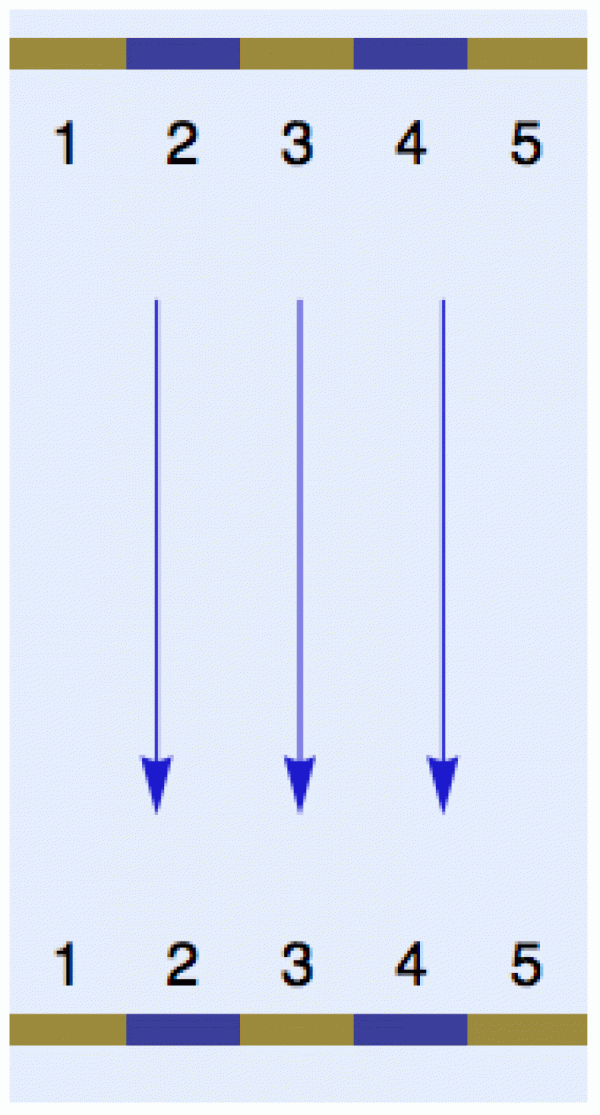
Představme si řeku, jejíž tok je příčně rozdělen na N malých bloků. V horní části toku (nahoře) vypustíme z nějakého bloku pingpongový míček a dole po proudu jej podběrákem vylovíme a zaznamenáme si číslo cílového bloku. Pokud je řeka dostatečně klidná, jako Labe pod Děčínem, cílový blok bude prakticky stejný jako ten startovací (míček z dvojky odchytneme pravděpodobně ve dvojce, maximálně tak ve trojce nebo v jedničce, zafouká-li větříček).

Teď ale experiment trochu pozměníme a mezi startovací a cílovou řadu umístíme divokou řeku, plnou kamenů, vraťáků, protiproudů a vírů. V tomto případě se klidně může stát, že míček vypuštěný z trojky vylovíme jednou z pětky a podruhé zase z jedničky. Pokud je voda dostatečně divoká, jako Orlice na Zemské bráně, budeme si moci číslo cílového bloku prakticky vytáhnout v loterii. Takový dynamický systém je nepředvídatelný.

Při studiu proudění kapalin si fyzikové dávno povšimli, že mezi laminárním a turbulentním prouděním je veliký rozdíl. A tuto dělicí čáru mezi předvídatelným a nepředvídatelným chováním můžeme pozorovat ve většině nelineárních dynamických systémů (tedy takových, které jsou popsány nelineárními funkcemi).

Jak přesně ztrátu struktury a předvídatelnosti charakterizovat, je do jisté míry otázkou názoru. Protože se zde kříží zájmy několika disciplín, terminologie není úplně ustálená. Nicméně pro potřeby tohoto článku budu používat následující zjednodušený slovníček.

nahodilý - nedá se určit dopředu, nedá se ovládat
chaotický - bez zřejmé struktury, neuspořádaný
komplexní - mající příliš mnoho parametrů, závisející na mnoha okolnostech
(v laickém kontextu se tato slova používají téměř jako synonyma)

Abychom se nemuseli bavit jen o ping pongu na řece, zopakuji z minulého Matykání schematický obrázek několika orbit z Kanekova 3D systému, na jehož chaotické vlastnosti si v závěru posvítíme. Zleva doprava vidíme ekvilibrium (bod, ke kterému orbity z okolí konvergují), periodickou orbitu (posloupnost bodů, po kterých definiční funkce přeskakuje jako po kamenech pořád dokola) a chaotický režim (kdy orbita z počátečního stavu bloudí po stavovém prostoru a nedaří se jí nikde se usadit - takové množině se často říká chaotický atraktor).

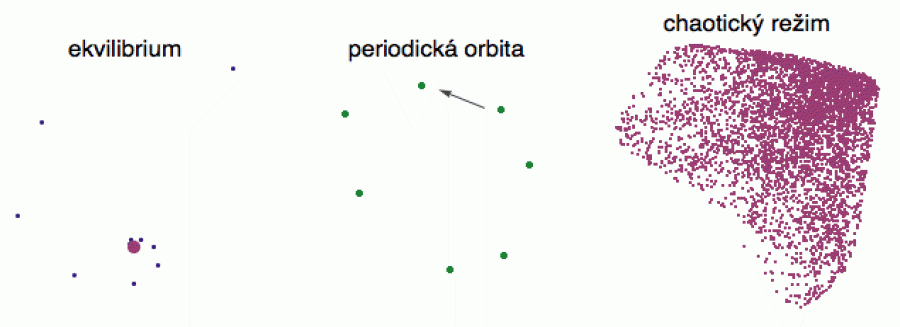
Všimněte si, že systém na obrázku vpravo je sice chaotický, v zobrazené orbitě není ani stopy po nějaké struktuře, ale přitom není komplexní (jsou to jen tři rovnice, jedna kvadratická a dvě lineární) ani nahodilý - přechod ze stavu x do stavu X probíhá podle zcela jednoznačně určeného pravidla (explicitně popsaného minule):

X = F(x).

Proto se tomuto typu chaosu říká deterministický. Pokud si budete házet kostkou, kam současný stav x nahodile popostrčit, výsledný obrázek bude možná podobný, ale povaha dynamiky bude úplně jiná.

Na druhé straně se některé komplexní systémy mohou chovat zcela předvídatelně (i když obecně komplexita vzniku chaosu napomáhá) a navíc si různé disciplíny jejich definici přizpůsobují svým potřebám. Sečteno a podtrženo: v používání tří základních termínů je, jak bych to tak řekl, no zkrátka chaos (a to ještě milosrdně pomlčím o entropii).

Abyste si nemysleli, že rozpoznat strukturu je nějaká brnkačka, ukážu vám pro začátek obrázek jedné jednoduché funkce f(t), kde čas běží na vodorovné ose. Kdo z vás pozná, zda zobrazuje dynamiku chaotického systému, ať hodí kamenem.

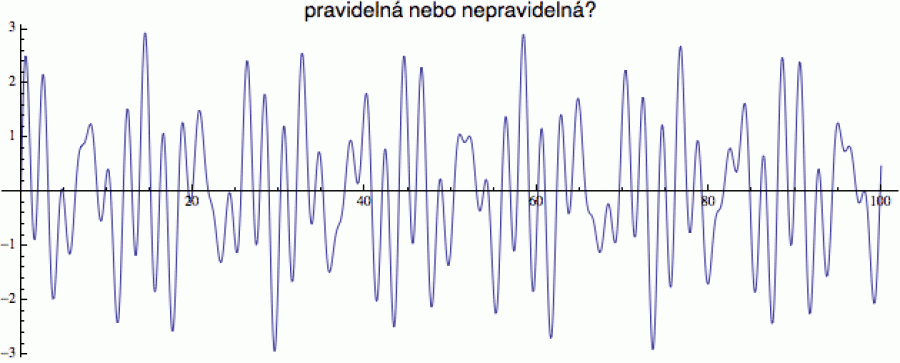
Na první pohled to vypadá, že funkce lítá bezhlavě nahoru dolů, bez jakékoliv struktury nebo periodicity, jako graf polohy neurotické berušky korzující zmateně po prádelní šňůře. Ale po bližším ohledání (a prokázala by to např. tzv. Fourierova analýza) by se ukázalo, že tato funkce vznikla součtem tří sinusoid

f(x) = sin(x) + sin(π * x) + sin(e * x), kde e a π jsou tradiční konstanty

Z toho vidíme, že definovat chaos nebo nahodilost není žádná legrace.

Abych nezabředl do konceptuálních filozofických bažin, ve kterých se dá bez problémů bídně utonout, ukážu vám v tomto příspěvku jeden konkrétní (a velmi typický) mechanismus, který v dynamických systémech k chaotickému chování vede. Je to expanze na konečném prostoru, kdy má systém sice tendenci se rozpínat, ale současně nemá kam, takže mu nezbyde, než se začít zaplétat sám do sebe - a to je první krok na cestě do chaotické džungle (existují ale i jiné způsoby, jak si podomácku vyrobit chaos - zkuste si třeba do uklizeného obýváku na půl hodiny pustit medvídka mývala).

Expanze na konečném prostoru

Aby bylo do toho rozpínání trochu vidět, podívejme se na úplně jednoduchý příklad diskrétního systému s celými čísly (aby se nám to lépe počítalo).

Na obrázku níže budu uvažovat dvě rozdílné dynamiky. A aby to bylo zajímavější, pro každou budu současně sledovat dvě orbity - modrou a červenou - vypuštěné ze dvou rozdílných počátečních stavů x = 2 a x = 3. A aby se nám body nezakutálely mimo výřez, budu vždy ukazovat zbytek po vydělení 59 (provedu tedy modulární redukci). Tím pádem se mohu při zobrazení omezit na čísla mezi 1 a 59. To bude můj „konečný prostor“. Na prvním řádku znázorním počáteční stav a na každém dalším řádku (směrem dolů) pak zobrazím iterace následujících definičních funkcí:

X= x + 2 (mod 59)
X = 2x (mod 59)

Na obrázku vlevo tedy při přechodu na další řádek přičtu k danému stavu dvojku (a pokud se vykutálím z intervalu (1, 59) vezmu zbytek, tj. 60 zobrazím na 1, 61 na 2 atd.) a na obrázku vpravo daný stav vynásobím dvojkou (takže na druhém řádku vidíme dvojnásobky počátečních stavů, tj. x = 4 a x = 6, a na třetím řádku dvojnásobky těchto, tedy x = 8 a x = 12)

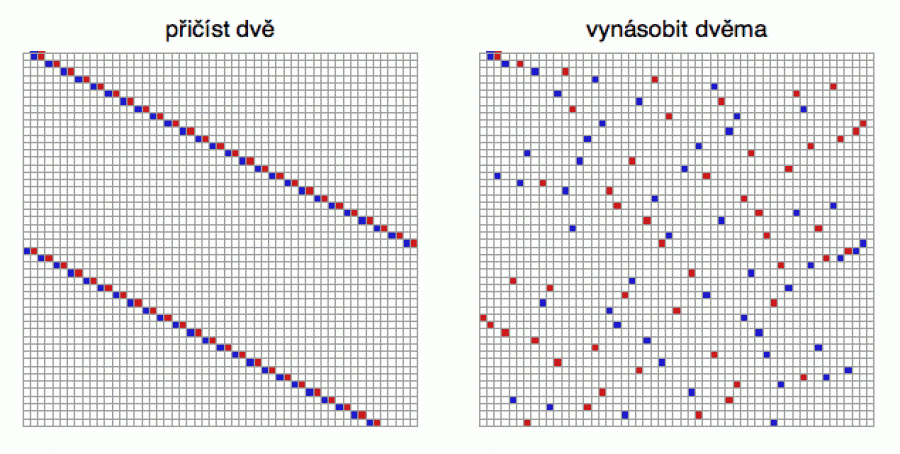
Vidíte sami, že nalevo se systém chová velmi krotce a že definiční rovnici nahoře byste asi sami uhodli. Vlevo ale řádí expanze - s každou iterací se rozdíl mezi červeným a modrým bodem zdvojnásobí. Kdybych nepočítal zbytky (tedy nechal čísla, jak jsou), tak by expanze prostě posílala body dál a dál směrem doprava na číselné ose a žádný velký chaos bychom nepozorovali (viděli bychom dvě exponenciální křivky s tím, že modrý bod by byl vždy menší než ten červený).

Tou kouzelnou ingrediencí podporující vznik chaosu je právě konečnost prostoru (zde implementovaná zbytkovou aritmetikou), na kterém si naše bodíky expandují. To ona ty dvě orbity začne promíchávat, takže napravo ty čtverečky vypadají, jakoby je povytahal papoušek z osudí.

(Upřímně řečeno, odborník na teorii čísel by nás poučil, že ani systém napravo není chaotický, protože se dříve nebo později zacyklí. Ale tento příklad s celými čísly, i když není úplně košer, hezky ilustruje, z čeho chaos vlastně pramení).

Expanzi na konečném prostoru si můžete představovat také takto: po vodní hladině budeme dvěma tryskami stříkat modré a červené barvivo. Kdyby trysky stříkaly v nějakém neomezeném médiu - třeba v moři - tak byste z letadla viděli prostě dva dlouhé expandující jazyky modré a červené. Ale v konečném bazénu dva proudy nemohou expandovat do nekonečna a dříve nebo později se začnou mísit. A to je přesně to, co způsobuje chaos. Promíchávání stavového prostoru následkem dynamiky je natolik klíčové pro pochopení statistických vlastností celého systému, že existuje podobor Teorie chaosu nazvaný Teorie míchání), který se pokouší nalézt kvantitativní vztahy mezi „intenzitou promíchávání“ a chaotičností systému.

Pokud si vezmeme asi nejznámější komplexní systém s chaotickým chováním - počasí - tak tam expanzi na konečném prostoru vidíme taky. Vzduchové masy by se chtěly rozpínat, ale nemají kam - planeta je konečná - a tak se mísí a proplétají a předpovědět se to pnutí a chrutí pořádně nedá.

V jistém smyslu je obětí tohoto principu - expanze na konečné planetě - i další známý komplexní (a nezřídka i chaotický) systém: geopolitika. Kdyby si národy seděly jen tak doma na zadku a nikam se necpaly, tak by nikdo nikam neexpandoval , veškeré interakce by se odbyly na úrovni obchodu a turistiky a geopolitici by neměli co řešit - ale to jen tak pro zasmání...

Expanze je také zodpovědná za jeden z nejcharakterističtějších průvodních jevů chaosu a to je citlivá závislost na počátečních podmínkách. Podívejme se opět nejprve na schematický popis.

Napravo vidíme systém, který neexpanduje. Představte si, že ze střechy podél modré trajektorie shodíte cihlu. Označíme si místo dopadu, pak popojdeme o vzdálenost da vlevo a shodíme další cihlu. Pokud zrovna nefouká vichr z hor, ta druhá cihla také dopadne o vzdálenost db = da vlevo. Tedy změna cílové polohy bude přímo odpovídat změně počáteční polohy. Takové matematické oko za oko, zub za zub - nic citlivého na tom není (také se na to můžete dívat takto: pokud se chcete trefit do nějakého cílového okénka o rozměru db, vaše startovní okénko by mělo být zhruba stejně široké).

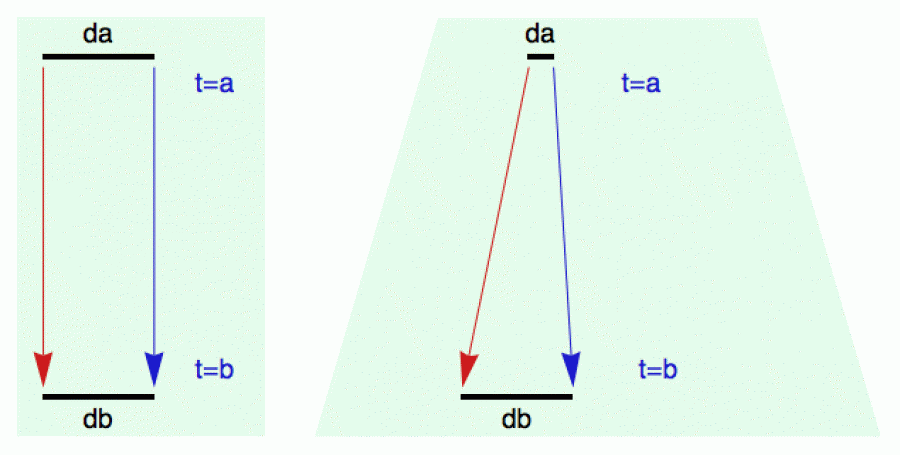
Pokud ovšem systém expanduje (viz vpravo), pak změny počáteční polohy expandují také. To znamená, že k dosažení cílové přesnosti db, potřebujeme na střeše cihlu vyhodit z podstatně menšího startovacího okénka da - jinak se netrefíme. Jinými slovy, malá změna da na vstupu dokáže vyvolat velkou změnu db na výstupu (jak velkou, to závisí na koeficientu expanze a na délce působení). A to je přesně to, čemu se říká citlivá závislost na počátečních podmínkách.

Hezky to ilustruje tento jednoduchý diskrétní model.

Vezmeme si zobrazení z intervalu (0,1) do intervalu (0,1), které zadefinujeme tak, že daný stav x pronásobíme deseti, celou část vzniklého čísla zahodíme a tu necelou si necháme jako následující stav X. Symbolicky si takové zobrazení můžeme opět zapsat pomocí modulární aritmetiky

X = F(x) = 10 * x (mod 1)
(toto je samozřejmě vysoce expanzivní zobrazení: koeficient expanze = 10)

Malý příklad: počáteční stav x = 0.46384 se naší dynamikou F zobrazí na číslo X = 0.6384 (a zahodili jsme 4), a po další iteraci na 0.384... (a vyhozena byla 6). Všimněte si, že N iterací tohoto systému prostě posune desetinný zápis o N pozic doleva (a co se přehouplo přes desetinnou tečku, jest nelítostně vyhozeno).

Na tomto systému jsou přímo vidět periodické orbity (stačí si vzít racionální číslo s periodickým rozvojem) i chaotický režim (jakékoliv iracionální číslo). Zda je chaotický režim nahodilý, je ovšem i u takto jednoduchého zobrazení oříšek. Dodnes například nevíme, zda číslo pí generuje číslice v desetinném rozvoji náhodně.

Abychom dynamiku F(x) pocítili na vlastní kůži, spojíme si ta „vyhozená čísla“ s nějakou akcí. Třeba 1 bude znamenat „zalít květiny“, 2 „hodit polštářem po manželce“, 3 „vyčistit psovi zuby“ atd.

Teď si vezmeme počáteční stav x = 0.311275... a po první iteraci vyčistíme psovi zuby (neb jsme vyhodili 3 a nový stav systému je X = 0.11275...), po druhé iteraci budeme zalévat (vyhazujeme 1), po třetí iteraci taktéž a po čtvrté iteraci budeme házet polštářem (vyhozeným číslem je 2). Na tomto příkladu krásně vidíte, že vaše „akce“ po N iteracích bude v podstatě záviset na N-tém desetinném čísle počátečního stavu (dobře si to rozmyslete).

Právě proto se tomu říká citlivá závislost na počáteční hodnotě. O tom, zda budete po 20. iteraci házet polštářem nebo dělat něco jiného, rozhoduje 20. desetinné místo vašeho počátečního stavu x. K tomu, aby se 20. desetinné číslo změnilo, samozřejmě stačí nepatrňoučká změna (doslova zafoukání větříčku) a vy budete místo čištění zubů psovi zalévat květiny. Na tomto modelovém příkladu také krásně vidíte, že čím dále do budoucnosti chcete něco předpovědět (tj. čím vyšší iteraci se snažíte uhodnout), tím přesněji musíte znát počáteční stav.

(Tomuto způsobu nazírání na chaos se říká symbolická dynamika a obvykle se praktikuje buď pomocí tzv. Smaleovy podkovy, a nebo pomocí dyadického zobrazení, které je de facto binárním ekvivalentem výše uvedeného F; je to velmi zjednodušený model, ale dobře ukazuje mechanismus, jak expanze „nafukuje" malé změny ukryté hluboko v desetinném rozvoji a protlačuje je do vyšších poloh, kde už mají hmatatelný vliv na realitu, což je přesně obsahem té citlivé závislosti.)

Velké následky způsobené malou změnou počátečního stavu popsané výše, se v populární literatuře někdy označují jako motýlí efekt. Motýlek někde zatřepotá křídly, masy vzduchu se malinko pohnou, takže někde na 30. desetinném místě se změní číslice, a pak už jen stačí počkat pár desítek iterací a nad New Yorkem se místo sluníčka objeví uragán - stejně jako v předchozím případě změna na 20. místě způsobí změnu akce (ve skutečnost je to s tím počasím samozřejmě podstatně složitější).

Mimochodem, podobný mechanismus používáme v praxi, když si házíme korunou. Malé bezděčné pohyby svalů a naše neschopnost je přesně kontrolovat v podstatě znemožňují přesné určení počátečních podmínek, které by nás dovedly k panně nebo orlovi. A čím více iterací (tedy zhruba čím vícekrát se koruna otočí ve vzduchu), tím přesnější bychom je potřebovali. Pokud si vezmete desetikorunu a budete celé odpoledne trénovat její házení tak, aby se jednou otočila a dopadla na tu samou stranu, možná se vám to i povede - obzvlášť máte-li dobrou svalovou koordinaci. Ovšem na to, aby se koruna ve vzduchu otočila desetkrát, už koordinaci mít nebudete - na to byste museli koruně udělit hybnost a rotaci s astronomickou přesností a vaše svaly prostě to „desáté“ desetinné místo nezvládnou (a malá změna v počátečních podmínkách pak způsobí velkou změnu po dopadu koruny).

Sekce jauvajs: Ljapunovovy exponenty
jen pro mimořádně otrlé povahy

Vzhledem k tomu, že pro chaotičnost systému je důležitá intenzita lokální expanze kolem dané orbity, je dobré mít po ruce nějakou míru, která nám prozradí, zda se body z okolí k dané orbitě x(n) při iteraci přibližují, anebo se od ní vzdalují a jak rychle. K tomuto účelu se v dynamických systémech používají tzv. Ljapunovovy exponenty.

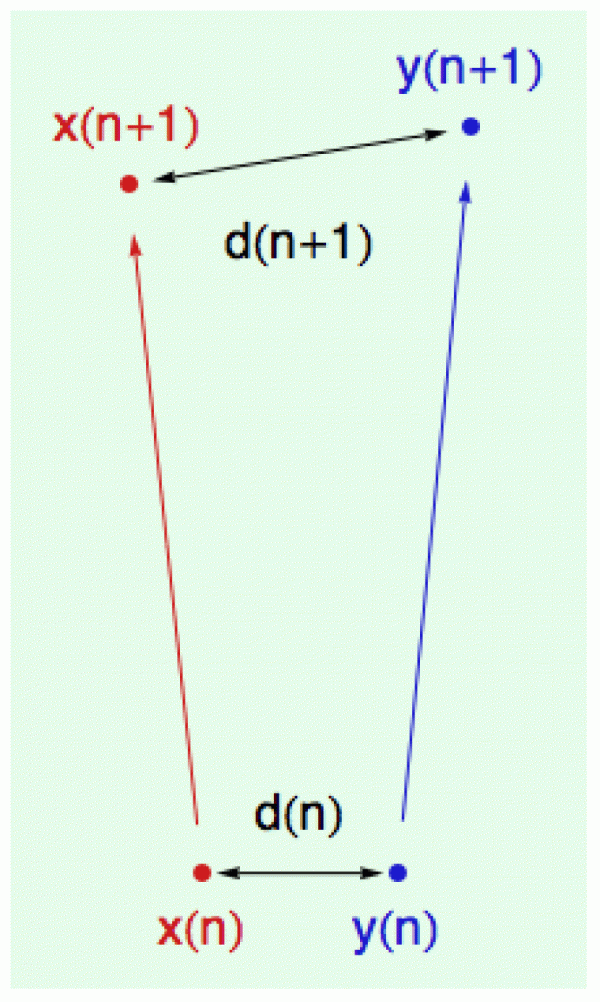
Definují se poměrně snadno (viz obrázek).

Vezmeme si dva počáteční body x(0) a y(0) velmi blízko sebe a budeme sledovat, jak se budou vyvíjet jejich orbity. Přesněji řečeno budeme sledovat, co se děje s rozdílem iterací

d(t) = x(t) - y(t)

konkrétně, jak se posloupnost d(t) mění s časem (a je jedno zda ten čas plyne spojitě anebo diskrétně). Pokud se obě orbity sbíhají, d(t) bude klesat, pokud se rozbíhají, bude stoupat.

Na kvantifikaci rychlosti růstu má matematika osvědčený recept a tím je exponenciální funkce v proměnné t (s parametrem a). Ze střední školy si vzpomeneme, že výraz exp(at) s časem roste, pokud je a kladné; klesá, pokud je a záporné; a nemění se, pokud je a rovno nule. A my se na růst naší funkce d(t) prostě pokusíme napasovat nejlepší možnou exponenciálu, jejíž koeficient a nám potom řekne, zda se orbity sbíhají, anebo rozbíhají.

d(t) ~ exp(at)
(zde ta vlnovka znamená, že hledáme a tak, aby exponenciála vpravo popsala funkci vlevo co nejpřesněji - to se obvykle musí spočítat limitou, ale tím se nenechme rozhodit)

Parametr a, který rozdíl orbit nejlépe popisuje, se jmenuje Ljapunovův exponent.

Samozřejmě pokud letíte podél dané vícerozměrné orbity v letadélku Káněti, klidně by se mohlo stát, že v některých směrech se k vám okolní orbity přibližují a v jiných se vzdalují. Počet Ljapunovových exponentů závisí na dimenZi prostoru, ve kterém dynamický systém operuje. A pokud dynamika zachovává objem (takovým systémům říkáme konzervativní), pak musí být expanze v jednom směru vyvážena kontrakcí v jiném směru (každý kladný exponent pak bude mít svůj záporný protějšek).

Pokud je exponent kladný, znamená to, že orbita y(t) se od té původní x(t) vzdaluje exponenciálně, takže náš systém obsahuje expandující složku - v tom případě můžeme očekávat chaotické chování. Mnoho autorů proto považuje kladný Ljapunovův exponent za jeden z příznaků (ne-li podmínek) chaosu (zdaleka ne každý se ale s takto silným tvrzením ztotožňuje).

Rigorózní definice chaosu - stejně jako definice nahodilosti - je poměrně obtížná věc a často se liší autor od autora.

Pokud se vám definice přes kladný Ljapunovův exponent nelíbí, můžete vzít zavděk poměrně rozšířenou, ba řekl bych až mainstreamovou definicí, kterou zavedl matematik Robert Devaney, a podle které je systém chaotický pokud splňuje tyto tři podmínky:

1. vykazuje citlivou závislost na počátečních podmínkách (to už jsme probrali)
2. je transitivní - to znamená, že dokáže stavový prostor dobře promíchávat; nebo ještě přesněji: kdykoliv si v tom stavovém prostoru X  vyberete dvě kuličky libovolné velikosti, tak dříve nebo později se vám iterace první kuličky protnou s tou druhou.
3. periodické orbity jsou v něm husté - to v podstatě znamená, že kdykoliv si vezmete malé okolí nějakého bodu, tak v něm naleznete periodickou orbitu - tedy bodík, který se působením iterací dokáže vrátit do původní polohy.

Na závěr této sekce vám představím Lorenzův atraktor, bez něhož by žádné pojednání o matematickém chaosu nebylo úplné.

Lorenzův systém je spojitý dynamický systém, který v roce 1963 popsal americký meteorolog Edward Lorenz, když studoval problematiku atmosférické konvekce. V podstatě si vzal obecné rovnice popisující proudění kapalin (Navier-Stokes), funkce v nich obsažené rozvedl do trigonometrických řad (tzv. Galerkinova aproximace), a tím získal obyčejné diferenciální rovnice svého modelu. Když ho začal dynamicky simulovat, tedy zkoumat, jak se body v daném silovém poli pohybují, ke svému překvapení zjistil, že jeho trajektorie nepravidelně rotují mezi dvěma ohnisky a nejeví žádné známky ustálení. Množinu, ke které se trajektorie systému přibližuje, dnes označujeme jako Lorenzův (podivný) atraktor. A protože je to 3D objekt, ukážu vám dvě jeho projekce do souřadných rovin.

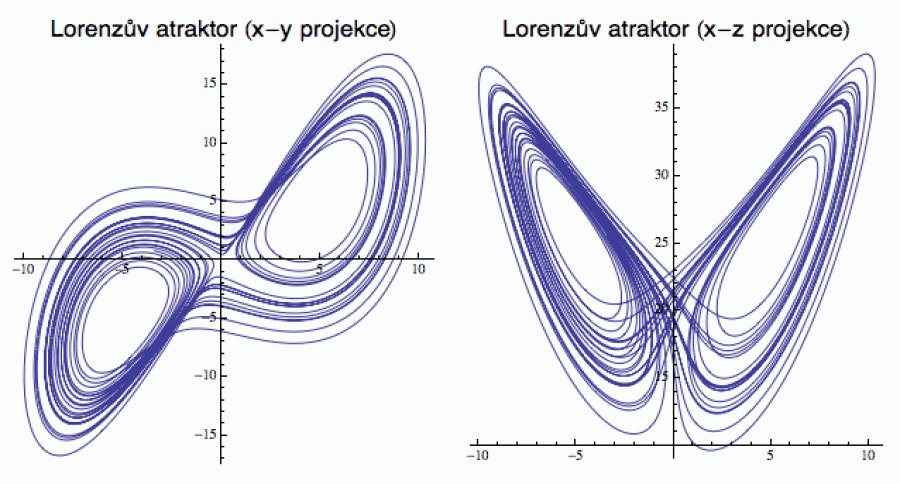
Na rozdíl od diskrétního Kanekova systému, kde orbita podél uzavřené křivky poskakuje, zde se orbita odvíjí spojitě. Pokud si chcete vychutnat chaotičnost tohoto systému v přímém přenosu, doporučuji vám tuto výbornou simulaci. A kdo by si chtěl spočítat jeho Ljapunovovy exponenty, může mrknout sem.

A jak tedy chaos vzniká?

Jedním slovem: chaoticky.

Přechod z uspořádaného režimu do neuspořádaného je postupný a nepravidelný. Nejzajímavější jevy obvykle najdeme v parametrickém rozmezí, kde se řád mísí s chaosem. Přesněji, kde v sobě nastupující chaos ještě stále nese ozvěny předchozí uspořádané struktury. Na hranici mezi těmito dvěma světy najdeme orbity, které mají dokonce jistou estetickou hodnotu.

Protože jsme si řekli, že za chaos je odpovědná expanze, musíme se podívat, co ji generuje. Minule jsme viděli, že při bifurkaci některé asymptotické objekty ztratí stabilitu a to znamená, že okolní body se od nich působením dynamiky začnou vzdalovat. Taková bifurkace je pak zdrojem expanze a klíčem k nástupu chaotického režimu.

Jako příklad si opět vezmu Kanekův systém (který je v podstatě 3D verzí Henonova zobrazení). Abyste si mohli některé zajímavější orbity vykreslit v lepším rozlišení, u každého obrázku najdete konkrétní hodnotu parametrů. Počáteční podmínkou je většinou bod (0,0,0). Prvních 5000 iterací vždy vyhodím, abych se zbavil transientů, a dalších 50000 vykreslím.

Asi nejběžnějším stabilním útvarem Kanekova systému je uzavřená křivka, podél které iterace systému poskakují, s tím že občas se při tom hopsání přesně trefí do hodnoty, kde už jednou byly, a pak se ta uzavřená křivka „zamkne“ v periodickou orbitu (jako na úvodním trojobrázku).

Na první ukázce budu při zafixovaném parametru a zvětšovat hodnotu c a ukážu vám, jak se uzavřená křivka začíná zvlňovat, když ztrácí stabilitu. Pokud si stabilitu představíme jako hloubku a strmost koryta, kterým projíždí kulička, není to nic překvapivého: čím je koryto mělčí, tím náchylnější bude kulička k pohybu do strany (je to tak trochu jako když jedete na kole: čím pomalejší jízda, tím je těžší udržovat přímý směr).

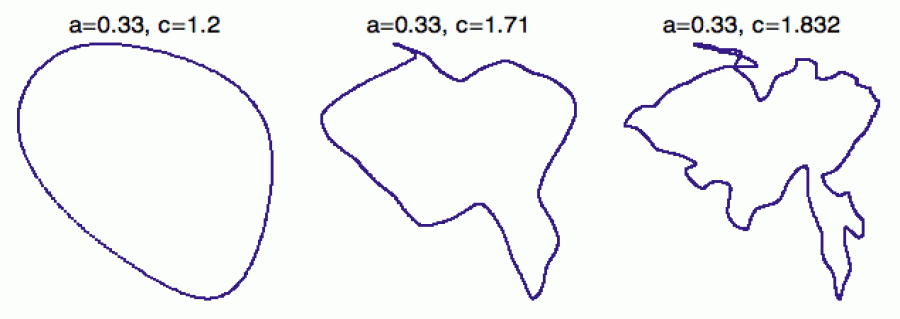
Jakým způsobem křivka ztratí stabilitu, záleží na hodnotě a. Někdy (vlevo) se části té křivky začnou štěpit (trochu to připomíná bifurkaci zdvojení peridy) a body pak při poskakování podél orbity projíždějí střídavě levým a pravým pruhem. Jindy (vpravo) to rozštěpení probíhá trochu živelněji.

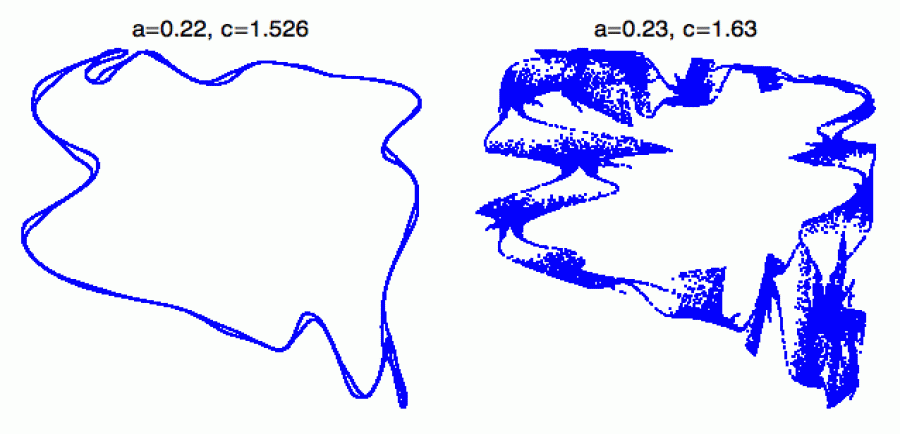
Občas se během rozštěpení uzavřená křivka kompletně rozpoltí na dvojkřivku (jako když máte dvoustopou autodráhu, kde si autíčka mohou vyměnit „dráhu“). Opět platí, že čím více je autodráha rozdrkaná, tím blíže je ztráta stability a chaotický režim.

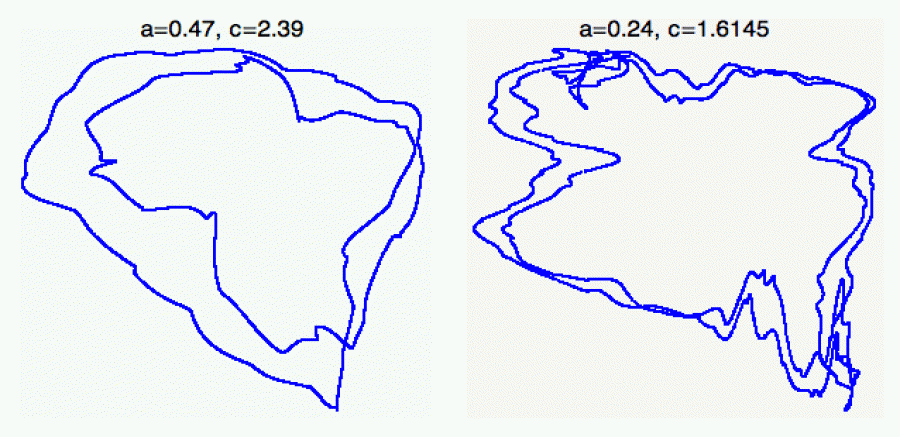
Pokud budete céčko nalevo zvyšovat velmi opatrně, uvidíte, že rozdvojená orbita se opět začne štěpit. Občas dokonce najdete orbity, které si při tom štěpení zachovávají jakési spojnice mezi oběma novými větvemi.

Teprve při dalším zvyšování céčka se orbita začne rozmazávat v chaosu. Ale nerozpadne se hned. Zbytky starých stabilních orbit (křivek) jsou ze začátku v chaotickém obláčku stále viditelné (a obláček sám stále ještě nevyplňuje celou oblast). Se zvyšujícím se céčkem bude protáhlý chaotický koridor pomalu zbytňovat, zatímco „jizvy“ po starých orbitách se budou postupně zahlazovat, až vznikne ten „beztvarý" chaotický režim z úvodního trojobrázku.

Jak jsem zmínil výše, pro jisté hodnoty parametrů se uzavřená křivka „zamkne“ a stane se periodickou orbitou. Pomocí Hopfovy bifurkce (viz minulé Matykání) se pak z každého bodu oddělí uzavřená křivka (vlevo) a ty se pak kolektivně rozsypou na malé souostroví chaotických obláčků (orbita zde přeskakuje z jednoho na druhý). Se zvyšujícím se céčkem se ostrůvky zvětšují, spojují se a nakonec se z nich opět stane jeden velký beztvarý chaotický atraktor.

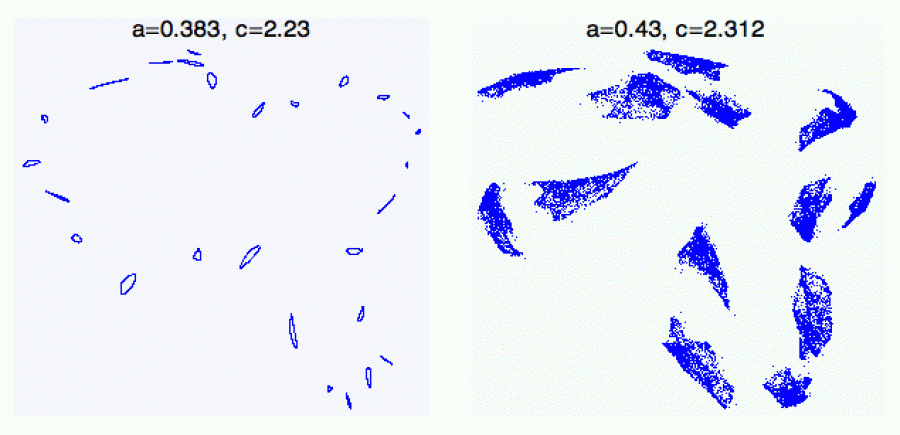
Jindy se stane, že ostrůvky jsou velmi protáhlé (jako Indonésie) a pak se dokáží spojit ještě před tím, než chaos ovládne scénu, a tím vzniknou zajímavé „polochaotické“ orbity (vpravo), kde základním hnacím motorem je stále uzavřená křivka. Ale jak orbita cestuje podél ní, už nedokáže držet „lajnu“ a pohybuje se opět v jakémsi chaotickém koridoru.

Při dalším zvýšení céčka se chaotický koridor rozšíří (jeho šířka je odvislá od míry nestability - trochu je to vidět v minulém Matykání, když si obrátíte obrázek vidlové bifurkace vzhůru nohama), orbita začne pomalu prozkoumávat i přilehlé oblasti stavového prostoru a posléze celou oblast vyplní tím náhodným chaotickým „zrněním“.

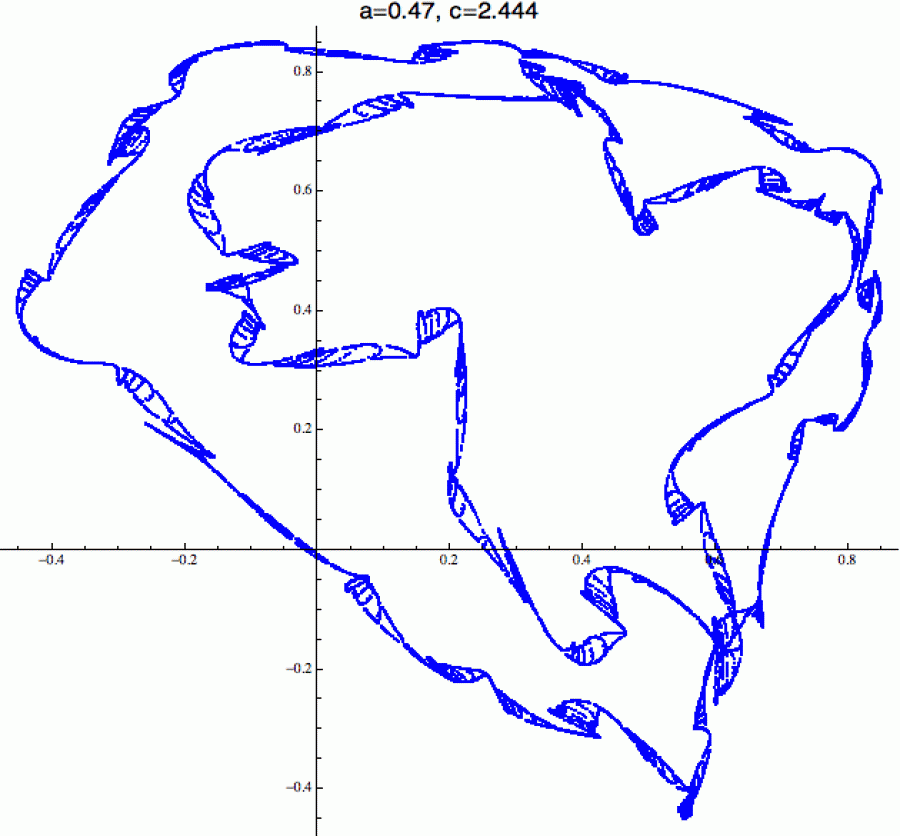
Tady jsou další dva obrázky uzavřených křivek „těsně před vypuknutím chaosu“. Tyto zajímavé útvary často existují jen ve velmi úzkém parametrickém intervalu, takže pokud je chcete objevit, musíte s céčkem šoupat velmi opatrně.

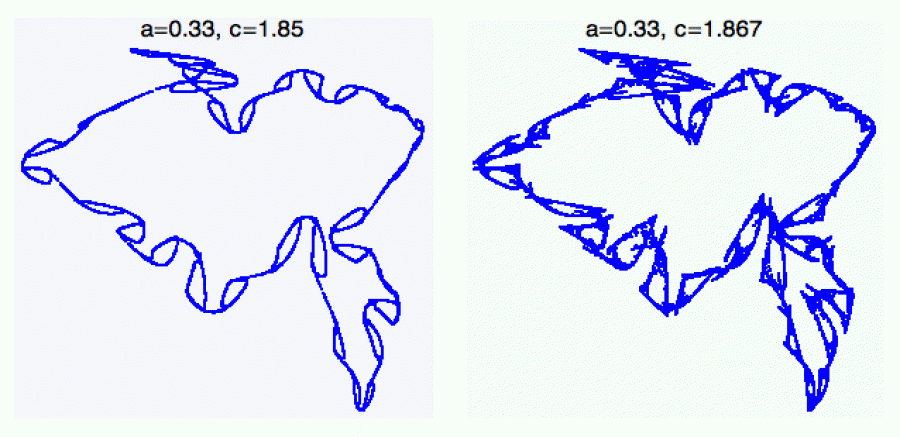
Na dalším obrázku už stojíme takřka na prahu chaosu. Tady hezky vidíte, jak expanze, která na konečném prostoru nemá kam expandovat, uzavřenou křivku rozkmitává až do absurdních poloh (důvod oscilací je ale poměrně technický).

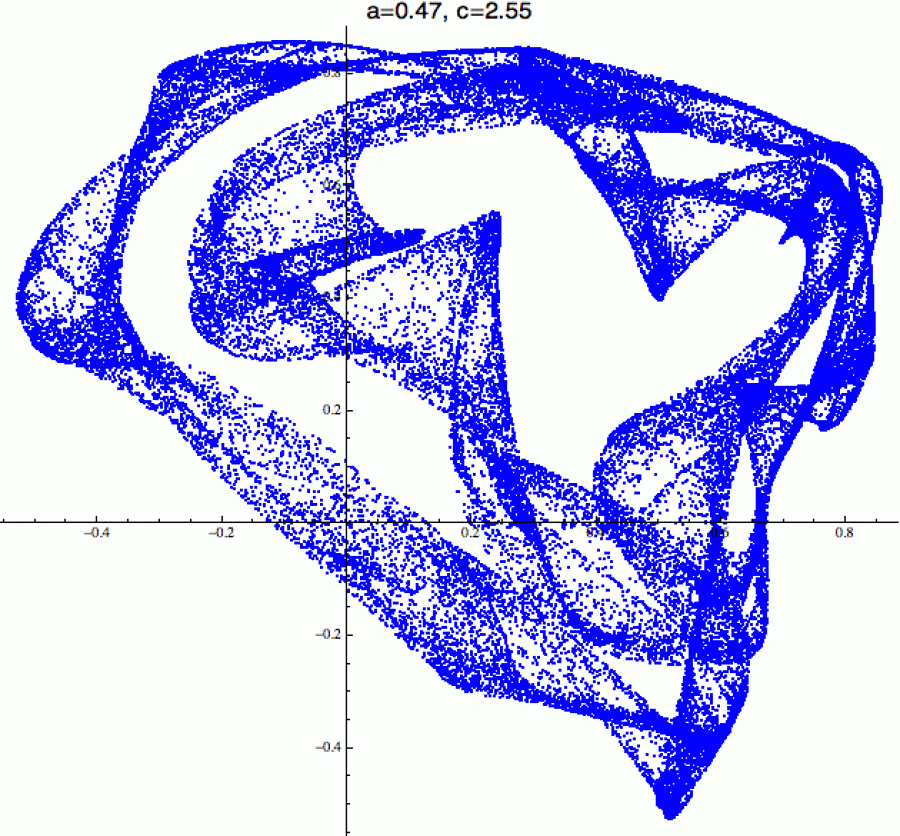
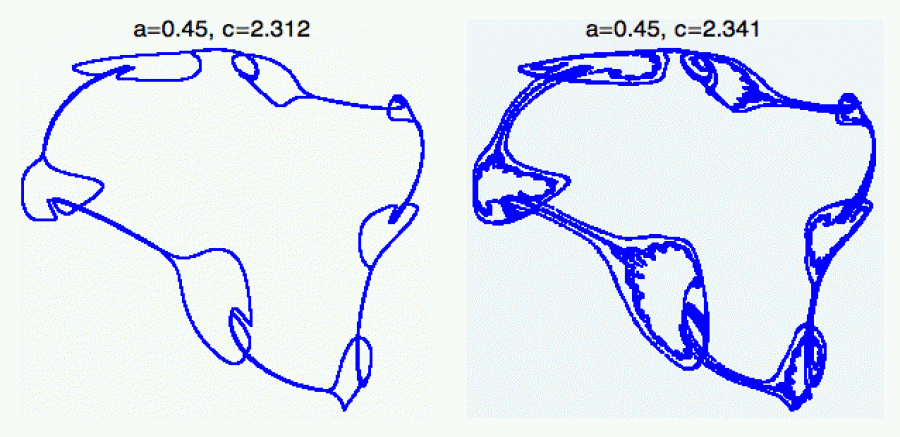
Tady jsem pro to samé áčko trochu zvětšil céčko. Když si tento obrázek porovnáte s předchozím, opět vidíte, že chaos předchozí struktury ještě úplně nesežral, ale pokud budete s céčkem pokračovat nahoru, nakonec jizvy předchozích orbit vyhladíte.

Na tyhle krasavce jsem narazil úplně náhodou (taky vidíte, že céčko už jsem musel navolit na tři desetinná čísla, jinak bych viděl jen obyčejnou periodickou orbitu). Ovšem jak takové orbity vzniknou, nemám vůbec tušení.

A těsně před vypuknutím chaosu se dokonce zahalí do této krajkoviny.

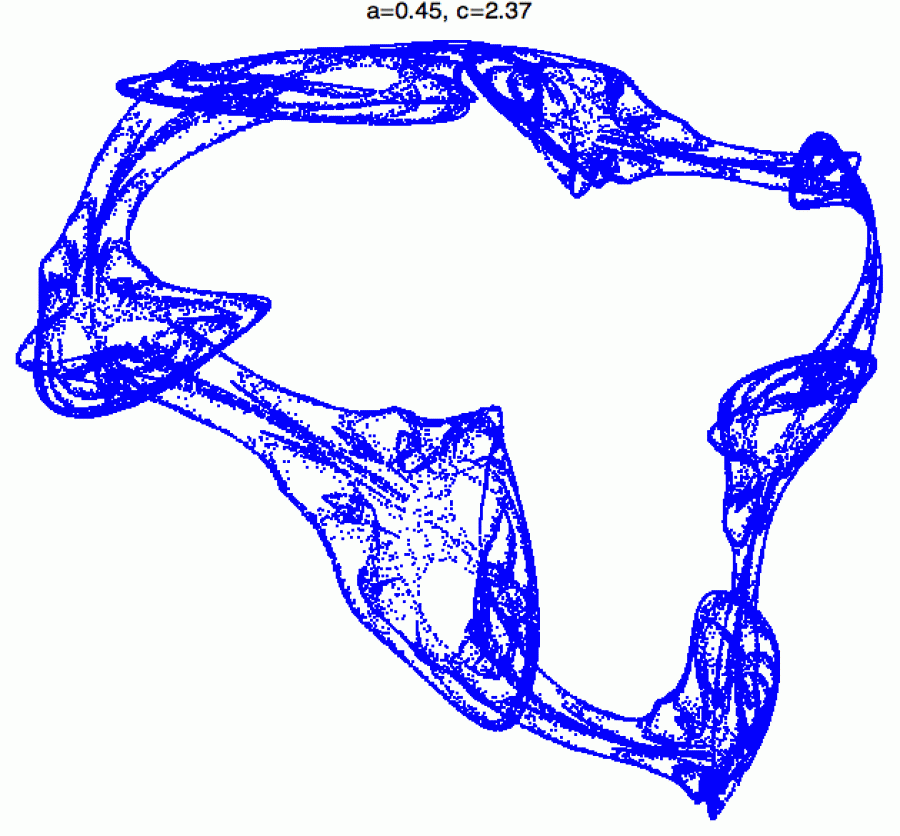
A pak už stačí malé ťuknutí do céčka a komplexní orbita z předchozích obrázků se začne rozplývat v chaotickém příboji.

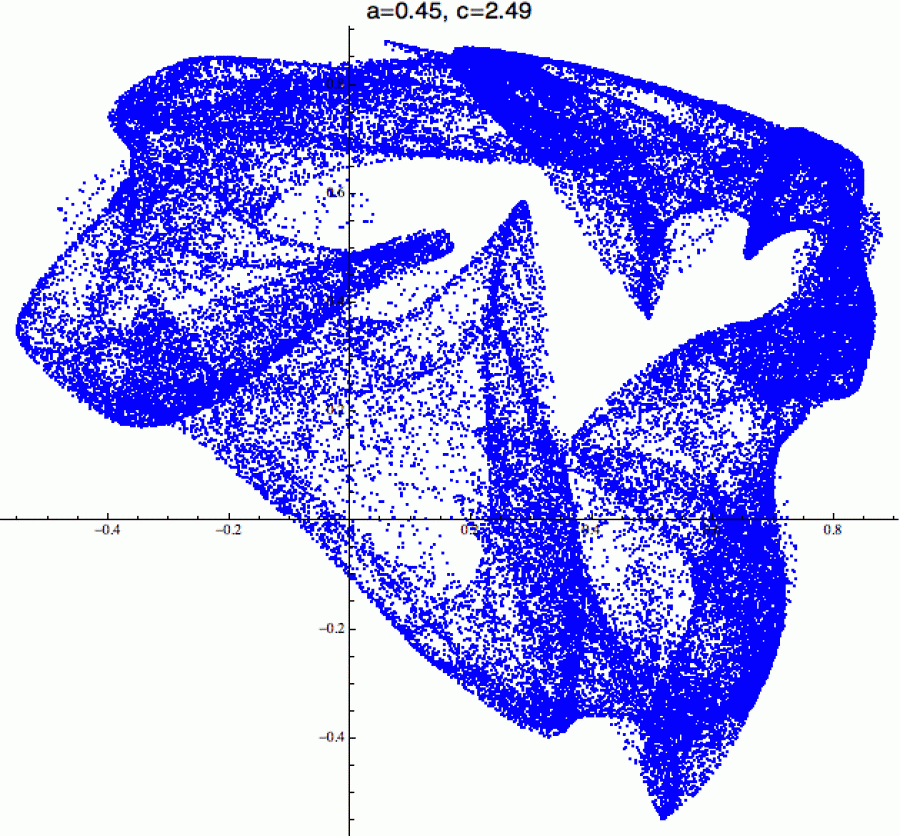
Celé to vypadá, jako když upustíte na zem jemný závoj. Všimněte si ale, že ten závoj je trochu jiný než ty předchozí, protože jsme se k němu dostali jinou posloupností bifurkací, takže jsou v něm vyřezány jizvy jiných uzavřených křivek. Nakonec se ale - stejně jako ve všech předchozích případech - dostaneme k chaotickému režimu ze začátku, ve kterém jsou všechny stopy jakéhokoliv řádu spolehlivě vymazány. Orbita už se pak nedrží žádné pevné struktury, ale hopsá si po prostoru jako opilá puberťačka v Kostelci na diskotéce, chraplavě vykřikujíc „Entropie vítězí“.

Z té citlivé závislosti na počátečních podmínkách plyne ještě jeden důležitý filozofický poznatek. Abychom mohli přesně predikovat chaotickou orbitu do budoucnosti, museli bychom umět spočítat její počáteční podmínky s libovolnou přesností. To ale nemusí být vždy možné: nejen proto, že zatím nemáme dostatečně citlivé přístroje, ale také proto, že sám prostor může být na subkvantové úrovni fundamentálně diskrétní anebo alespoň zvířený takovým způsobem, že se v něm přesná poloha zjistit nedá. Pak je samozřejmě s dlouhodobou predikcí chaotických systémů definitivní utrum.

Nabízí se tedy změna paradigmatu. Nasadíme si brýle statistiky a už se nebudeme ptát, zda za rok bude systém tady anebo tamhle, ale budeme se ptát, jaká je pravděpodobnost, že za rok bude systém v této oblasti, anebo v tamté. Z posledního obrázku je vidět, že pravděpodobnostní počet se na popis takových systémů hodí lépe. Některé oblasti mají z pohledu orbity větší šanci na návštěvu než jiné a zkoumat průměrnou hustotu bodů je obecně snazší, než se trápit s přesnou polohou každého z nich (tento pohled rozvíjí např. tzv. ergodická teorie).

A proto i my příště opustíme deterministický svět a vydáme se do říše náhod.

Pokud jste si pustili Lorenzův atraktor dynamicky, možná vás napadlo, že ty chaotické rotace kolem dvou ohnisek by se měly dát algoritmicky přetvořit v posloupnost tónů. A přesně to realizoval Steve Gilliland na následujícím oddechovém videu s pomocí programu FractMus.

Článek je redakčně upravenou verzí blogového příspěvku na serveru iDNES.cz. Publikováno s laskavým svolením autora.

Další díly a původní texty jsou dostupné na blogu Jana Řeháčka.

Autor: Jan Řeháček