My, lidé, počítáme v soustavě desítkové, protože máme deset prstů. Počítače mají prsty jen dva (proud teče, anebo neteče), a tak počítají v soustavě dvojkové. V dnešním Matykání se právě této soustavě podíváme na zoubky. Na oba.

Jen co se naši předkové naučili používat mozkovnu ke složitějším operacím, než jen k výpočtu únikové cesty před rozmrzelým mamutem, seznali, že věci kolem nás existují v různých kvantitách. Někdy narazíme na jednoho chlupatého masodárce, jindy na tři a někdy na stádo čítající 25 hlav a odpovídající počet chobotů. A protože kvantita měla na životní styl tlupy rozhodující vliv, zrodila se potřeba si ji navzájem sdělovat. A z tohoto zájmu vznikla čísla, o něco později i počty a nakonec sama matematika.

V mysli většiny lidí jsou čísla nerozlučně spjata s jejich dekadickým zápisem (tedy zápisem v desítkové soustavě). To ale není jediný možný způsob, jak danou kvantitu zaznamenat. Abychom se mohli popasovat s problémem počítání v jiných číselných systémech, musíme ve svém myšlení v první řadě oddělit abstraktní pojem kvantity od zcela konkrétního zápisu daného množství v určitém všeobecně přijatém formalismu.

Představte si, že se blížíte k osamocenému dubisku v poli se skupinkou cizinců. „Strom!“ zvoláte s nadšením, a pokud jste jako prezident, přátelsky jej obejmete. Ovšem to, co je pro vás „strom“, je pro Angličana „the tree“, pro Němce „der Baum“ a pro Poláka „drzewo“. Nezúčastněný pozorovatel by si mohl myslet, že každý koukáte na něco jiného. Ale není tomu tak. Strom, ten objektivně existující dub před vámi, je pro všechny pozorovatele úplně stejný, přestože jste mu každý přiřadil jinou verbální nálepku.

S čísly je to podobné. Představme si, že máme na stole sto dvacet devět piškotů. To je zcela reálná, jednoznačně určená a v tomto případě zcela hmatatelná kvantita. Na vašem mentálním displeji vám nejspíš automaticky naskočí číslovka 129. Ale pozor - to už je pouze desítková (dekadická) nálepka, kterou na kvantitu připlácnete ve svém konkrétním desítkovém jazyce. Čtyřprstý Marťan pocházející z jiné planety by mohl při pohledu na tu samou hromádku piškotů klidně vytasit osmičkovou číslovku 201 a měl by svým způsobem také pravdu (viz následující sekce). Kdybychom se mu snažili podstrčit naši dekadickou číslovku 129, koukal by na nás jako zjara - stejně jako ten Angličan, který zná strom pouze jako „tree“. Zkrátka než se pustíme do tvrdého počítání, musíme být schopni ve své vlastní hlavě jasně rozlišit pozorované množství (konkrétní hromádku piškotů na stole) od nějaké pomocné nálepky (129 pro pětiprsté lidi, CXXIX pro staré Římany a třeba 201 pro čtyřprsté Marťany).

Zkrocení kvantity a její zapřažení do myšlenkového jha nebyl jednoduchý zápas. Na jeho počátku byl počet zářezů na opasku, kterým si lovci navzájem sdělovali počet přemožených mamutů. To by ale v případě jejich přemnožení nebylo právě praktické, a tak lidstvo přešlo k nejrůznějším symbolickým zápisům. K nejpropracovanějším patřily římské číslice. Namísto 44 zářezů byste si na opasek jednoduše vyškrábali XLIV (tedy pokud by se nějací mamuti takových krásných číslic dožili). Tento způsob zápisu byl velkým krokem dopředu, protože zavedl mezi symboly jakousi hierarchii, byť tato nebyla zrovna nejlépe uzpůsobena pro praktické počítání - např. číslovky předřazené hodnotu ubírají (IX = 9), zatímco číslovky zařazené ji zvyšují (XI = 11). A teď se v tom, kozle, vyznej. Nebo si dvě takové římské vymyšlenosti sečti.

Nakonec se lidstvo propracovalo k tzv. pozičním systémům. A o nich bude tento příspěvek. V první části se podíváme na jejich mechaniku a nahlédneme jim trochu pod kapotu. Druhá část bude věnovaná aplikacím těchto systémů v počítačích.

Protože budu různě žonglovat s číselnými zápisy, dohodněme se, že pokud napíšu 129, bude to znamenat klasicky sto dvacet devět, tak jak jsme zvyklí v desítkové soustavě. Pokud budu chtít použít zápis v nějakém jiném systému, třeba v osmičkovém (jako ti čtyřprstí Marťani), napíšu dané číslovky v závorce - např. (201) - s tím, že z kontextu bude patrné, v jakém systému máme číslovky interpretovat.

Násobení budu provádět znakem * (takže 2 * 7 je dva krát sedm). Dále budeme potřebovat mocniny, pro které si vypůjčím znak ^ (příklad: 10^2 bude znamenat deset na druhou). A konečně ze střední školy vám připomenu, že nultá mocnina kladného čísla je vždy jednička (příklad: 10^0=1). Proč? Proto!

Poziční číselné systémy

Abychom mohli desítkovou soustavu zobecnit, musíme nejdřív přesně pochopit, jak vlastně funguje. Desítková soustava rozkládá dané číslo na mocniny desítky (10^0=1, 10^1=10, 10^2=100, 10^3=1000 atd.) a při čtení číslovky zprava doleva přesně vidíme, kolik kterých mocnin je v čísle obsaženo. Tomu kouzelnému číslu (zde 10), jehož mocniny při rozkladu používáme, se říká základ. Takže našich 129 piškotů znamená, že v kvantitě na stole je obsaženo 9 jednotek (nulté mocniny), 2 desítky (první mocniny) a 1 stovka (druhé mocniny). Symbolicky 129 = 9 * 1 + 2 * 10 + 1 * 100.

Při interpretaci číslovek z jiných číselných systémů postupujeme obdobně, jen místo mocnin 10 používáme mocniny nějakého jiného základu a to je celá věda. Jméno systému se pak většinou odvozuje od tohoto základu (dvojkový/binární, trojkový/ternární, osmičkový/oktální, desítkový/dekadický/decimální, šestnáctkový/hexadecimální atd.)

Jako příklad si vezměme třeba zmíněných (201) zapsaných v osmičkové (oktální) soustavě. V této soustavě jsou základními stavebními kameny mocniny osmi - tj. 8^0=1, 8^1=8, 8^2=64, 8^3=512 atd. Číslo v závorce nám de facto říká, kolik kterých stavebních kamenů v našem čísle vlastně máme. Převod zpátky do standardní (desítkové) soustavy je poměrně jednoduchý, jen nezapomeňme místo mocnin desítky sčítat mocniny osmičky (opět zleva doprava). V osmičkovém čísle (201) máme jednu nultou mocninu (1), nula prvních mocnin (8) a dvě druhé mocniny (64). Suma sumárum to dělá 1 * 1 + 0 * 8 + 2 * 64 = 129. Výsledné množství piškotů je stejné! To jsme si oddychli... (mimochodem, osmičkové číslo můžete skládat i zleva doprava, ale musíte si nejdřív správně spočítat, jakou nejvyšší mocninu základu v něm máte - zde druhou: 129 = 2 * 64 + 0 * 8 + 1 * 1).

O něco tvrdší oříšek je, když nám někdo zadá kvantitu (v desítkové soustavě) a pak nás požádá, abychom ji převedli do nějaké jiné - třeba opět do osmičkové, tedy se základem 8. Ve školách se na to konto učí různé algoritmy, vzorečky a postupy, ale dá se to zvládnout prostými kupeckými počty. Naším cílem je vyjádřit zadané číslo pouze pomocí mocnin daného základu (zde 8), a tím vypátrat jeho osmičkové číslovky (všimněte si v předchozím příkladu, že osmičkové číslovky jsou ty „koeficientíky“ stojící při různých mocninách osmičky!). Na tento problém se můžeme dívat tak, že si představíme bankovky v nominální hodnotě mocnin základu - v tomto případě 1, 8, 64, 512, 4096,... a pak se pokusíme zadané číslo „zaplatit“ těmito bankovkami. Kdo dobře ovládá aritmetiku, měl by to zvládnout selským rozumem. Vezměme si například číslo 700 a vyjádřeme jej v osmičkové soustavě. Jinými slovy, máme provést platbu částky 700 a k dispozici máme pouze výše uvedené bankovky, přičemž vyšší bankovky mají přednost (tím chci pouze říci, že máte-li zaplatit 20 Kč, a v peněžence máte jednu dvacetikorunu a dvě desetikoruny, tak na pult položíte tu dvacku). Kolik jakých osmičkových bankovek tedy vysolíme při zaplacení 700 Kč?

V první řadě se podíváme, jaká nejvyšší mocnina daného základu je v našem čísle obsažena (tedy jakou nejvyšší bankovku budeme potřebovat), a pak budeme ve zbytku lovit mocniny menší (tj. zbytek částky budeme doplácet bankovkami s nižší hodnotou).

Největší bankovka (mocnina osmičky) v čísle 700 obsažená je 8^3=512 (tou další, což je 4096, už bychom přeplatili). Tato bankovka je v našem čísle obsažena jen jednou, s tím že nám zbyde k doplacení 700-512, což je 188. Teď už nám ta „pětisetdvanáctikoruna“ nepomůže, takže sáhneme po nejbližší nižší bankovce, kterou je „šedesátičtyřkoruna“. Číslo 64 je v našem zbytku obsaženo dvakrát (třikrát už bychom přeplatili: 3 * 64 = 192). Takže na stůl vyplázneme dvě „šedesátičtyřkoruny“ a zbyde nám k doplacení: 188 - 2*64 = 60. No a ten poslední zbytek, tedy 60, už lehce proplatíme „osmikorunami“ (první mocniny našeho základu) a „korunami“ (nulté mocniny). Kdo ovládá malou násobilku, ví, že „osmikorun“ budeme potřebovat sedm, protože 7 * 8 = 56 (8 * 8 = 64 a to už bychom opět přeplatili). Zůstanou nám k doplacení čtyři kačky, které uhradíme čtyřmi „jednokorunami“. Takže 700 Kč se zaplatí takto: 1*512 + 2*64 + 7*8 + 4*1. Anebo pomocí mocnin: 700 = 1 * 8^3 + 2 * 8^2 + 7 * 8^1 + 4 * 8^0. Tímto se nám povedlo částku 700 vyjádřit pomocí našich „bankovek“ (mocnin osmičky) a to je vše, co potřebujeme k zápisu tohoto čísla v osmičkové soustavě. Teď už si jen z rovnice vytáhneme koeficienty stojící u mocnin osmičky: 700 = (1274). A je to. Na levé straně máme desítkový zápis, na pravé osmičkový. Je to něco, jako bychom napsali: „strom“ = „tree“.

Protože tohle je poměrně zapařený výpočet, dáme si ještě jeden příklad. Převedeme si (dekadické) číslo 19 do dvojkové soustavy. Mocniny dvojky jistě znáte - v naší peněžence se tentokrát budou nacházet bankovky o hodnotě 1, 2, 4, 8, 16, 32,... Naším úkolem opět je pomocí těchto bankovek „zaplatit“ částku 19 Kč.

Nuže, nejvyšší bankovka, kterou naši částku nepřeplatíme, je 16 (2^4). Ta je v něm obsažena právě jednou a zbyde nám (pro další splátky) 19-16 = 3. Další nižší bankovka je 8 a ta v tom zbytku není obsažena ani jednou. Další je 4 a ani ta ve zbytku obsažena není. Teprve bankovka s hodnotou 2 (dvoukoruna) v našem zbytku obsažena je, a to jednou. Odečteme 3-1*2 a zůstane nám pro finální krok pouze 1, což splatíme jednou korunou. Máme tedy 19 Kč = jedna šestnáctikoruna, nula osmikorun, nula čtyřkorun, jedna dvoukoruna a jedna koruna. Symbolicky: 19 = 1 * 2^4 + 0 * 2^3 + 0 * 2^2 + 1 * 2^1 + 1 * 2^0. A koeficienty stojící u mocnin dvojky nám opět vytvoří dvojkový zápis daného čísla: 19 = (10011). Ve finálním účtu musíme zaznamenat i bankovky, které jsme nepoužili (!), protože jinak by se nám číslovky pošouply někam, kam nepatří. Kdybychom napsali pouze (111), tak bychom dostali úplně jiné číslo - zde konkrétně 7.

Ale na to jsme zvyklí i z desítkové soustavy, že nuly se musí vypisovat: 2078 je něco úplně jiného než 278! Na procvičení tohoto bankovního postupu si můžete zkusit ověřit, že číslo 54 se v pětkové soustavě zapíše jako (204).

Mimochodem, všimněte si, že v soustavě osmičkové použijete pouze číslovky 0 až 7, protože jakmile se při počítání jednotek dostanete k 8, tak už jste u dalšího stavebního kamene (vyššího řádu) a můžete těch 8 de facto napsat jako (10). Tomu odpovídá, že 8 Kč nezaplatíte osmi „jednokorunami“, ale jednou „osmikorunou“ (to je pravidlo o použití nejvyšší možné bankovky). Takže číslovku 8 v osmičkové soustavě vůbec nepotřebujeme (stejně jako v desítkové nepotřebujeme zvláštní symbol pro „deset“ - místo toho napíšeme zkráceně „jedna nula“). Rozmyslete si, že v osmičkové soustavě je přechod od (77) ke (100) vlastně to samé, co v desítkové přechod od 99 ke 100. Obecně tedy platí, že v číselné soustavě o základu N potřebujeme pouze symboly pro číslovky 0, 1, ... N-1. Konkrétně ve dvojkové si vystačíme s 0 a 1.

Pokud je náš základ menší než deset, nemáme problém. Pak prostě jako symboly používáme pouze číslovky, které potřebujeme, a zbylé necháme koňovi. Horší to je, když chceme počítat v soustavě, řekněme, šestnáctkové. V ní budeme potřebovat symboly pro čísla od nuly až do patnáctky (a pro patnáctku nemůžeme použít zápis jedna-pět, protože to by v šestnáctkové soustavě znamenalo 116+51, což je 21, a z toho by vznikl pěkný maglajs). V praxi se to řeší tak, že od nuly až do devítky bereme standardní číslice z desítkové soustavy, a pro ty další si pak půjčujeme písmenka s následujícími významy: a=10, b=11, c=12, d=13, e=14 a f=15. Pokud nám tedy někdo zadá číslo v šestnáctkové soustavě jako (7b1), tak nezpanikaříme, ale opět ho rozepíšeme v mocninách 16 s tím, že písmenkům přisoudíme výše uvedený význam (b tedy bude reprezentovat 11). A teď si na to šestnáctkové číslo můžeme posvítit (a pokud si nejste jistí v kramflecích, čtěte to opět zprava doleva, počínaje jednotkami): (7b1) = 1*1 + 11*16^1 + 7*16^2 = 1969 (jedenáctka pochází z prostředního béčka!). Takže šestnáctkové číslo (7b1) odpovídá v desítkové soustavě číslu 1969.

Někdy je jedna tabulka lepší než tisíc příkladů, takže tady je prvních dvacet čísel v různých soustavách. Můžete si je ověřit sami za domácí cvičení.

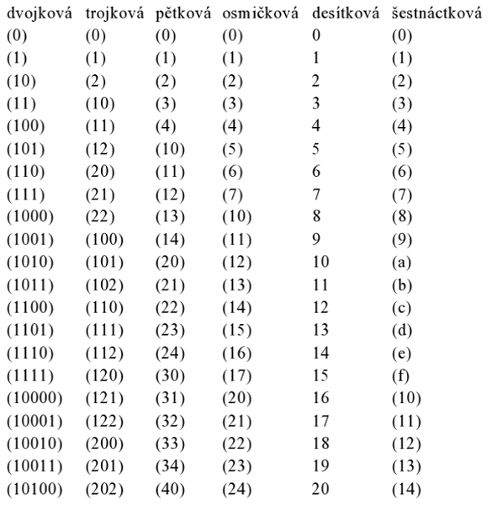
A tady je nádavkem ještě pár větších čísel v rozmezí od 248 do 258. Ať nežeru.

Sečteno a podtrženo: každý řádek vyjadřuje de facto stejnou kvantitu. Předposlední sloupek si můžete představit jako její vyjádření v „češtině“ (něco, na co jste zvyklí), zatímco v ostatních sloupcích vidíte vyjádření téže kvantity v „cizích jazycích“.

Bity, bajty a hexadecimální příšerky

S tím vším, co bylo řečeno, bych teď mohl článek uzavřít konstatováním, že počítače počítají v soustavě dvojkové (binární), a místo pracného převádění bychom mohli zajít na pivo. Protože se ale určitě doma nudíte, tak se v tom budu ještě chvilku rejpat.

Nejdřív se podívejme, jak se v takové dvojkové soustavě počítá. Je to podobné jako v desítkové - tedy sčítáme odpovídající číslovky, a pokud se dostaneme „přes desítku“, přesněji „přes dvojku“, tak přenášíme do vyššího řádu.

Zkusme si třeba počítačově sečíst 5 a 6, což je ve dvojkové soustavě zapsáno jako (101) a (110). Napíšeme si čísla pod sebe a jedem. Zprava doleva!

101
110

Jedna a nula je jedna, takže vpravo napíšeme jedničku. Prostřední sloupec: nula a jedna je jedna, napíšeme opět jedničku. Levý sloupec: jedna a jedna je ve dvojkové soustavě (10), takže napíšeme nulu (a jedničku přeneseme do vyššího řádu). Tam už nic jiného není, takže jedničku napíšeme na čtvrtou pozici (zprava) a jsme hotovi. Dostali jsme výsledek ve dvojkové soustavě (1011) a to není nic jiného než jedenáct (1*8 + 0*4 + 1*2 + 1*1) - jak ostatně očekáváme. Ve skutečnosti je sčítání celých čísel o něco málo komplikovanější, ale v zásadě probíhá tak, jak jsme si ukázali.

Dvojkovým číslovkám - v posledním příkladu 1,0,1,1 - se říká bity, a jak plyne z předchozí sekce, každý takový bit může nabývat pouze hodnotu nula nebo jedna, což si můžeme vyložit jako „ne“ a „ano“. Bit je tedy v jistém smyslu nejmenší jednotkou informace. To, zda venku prší nebo neprší, se dá zakódovat jako 0=neprší a 1=prší. Spočítání bitů (dvojkových číslovek) nám umožní určit, kolik paměti bude náš počítač potřebovat, aby si mohl daný výsledek „zapamatovat“. Třeba v tom posledním výpočtu jsme se dobrali k dvojkovému výsledku (1011), což jsou čtyři binární číslovky. Aby si je tedy náš počítač mohl „pamatovat“, bude potřebovat 4 bity. Když se podíváte na poslední tabulku nahoře, zjistíte, že na číslo 258 už bychom potřebovali 9 bitů, jinak se nám do paměti nevejde. Čím větší číslo, tím více bitů na jeho vyjádření potřebujeme. V desítkové soustavě je to ostatně podobné: větší čísla spotřebují na své vyjádření víc dekadických číslic.

Chvilka oddechu (zhruba 4 zalapání po dechu): Představte si, že jste kapitánem přepravní lodi a děláte si inventuru: jeden zákazník stěhuje piano do Číny, druhý chce přepravit do Thajska čtyři basy Prazdroje, třetí potřebuje dopravit 80 pytlů cementů na Tchaj-wan, čtvrtý si nechal ve Škodovce vyrobit náhradní ložisko do vietnamského kolotoče, a pátý si objednal převoz živého slona z Indie do Laosu. Když budete takový náklad v úložném prostoru rovnat, tak z toho chytíte amok, protože ty bedny a pytle a klece a přepravky k sobě prostě nepasujou a nepasujou. Z toho důvodu si přepravci vymysleli báječnou věc: kontejner. Ten má normalizované rozměry, takže se lehce skladuje i překládá z lodi na loď, a co si naložíte dovnitř, je kapitánovi šumafuk. Klidně pojízdnou míchačku betonu.

V počítačích to funguje podobně. Vzhledem k tomu, že různá čísla zabírají různý počet bitů (podle toho, jak jsou velká), naše výpočetní miláčky by z jejich skladování brzy rozbolela binární hlavička. Proto si programátoři za účelem usnadnění manipulace vymysleli malé normalizované „kontejnery“ o velikosti 8 bitů (říká se jim bajty - anglicky byte) a s nimi pak v počítači šibují, jak uznají za vhodné. Jeden bajt je tedy roven osmi bitům (i když existují exotické systémy, které mají kontejnery nastavené maličko jinak). Prakticky všechno, s čím v počítačích přijdete do styku, se přenáší či skladuje pomocí těchto bajtů (kontejnerů). Až si jednou roboti a androidi sepíšou své vlastní Evangelium podle sv. Jana, bude bezpochyby začínat slovy: „Na počátku byl Bajt“.

Pokud jste „bajt“ (byte) nikdy neviděli, tady je malý příklad: (10011101). Tak ho vidí interně počítač. Je to vlastně jenom malá skupinka 8 binárních číslovek (bitů). Do jednoho bajtu se tedy dá nacpat 256 = 2^8 různých hodnot - ve dvojkové soustavě zapsaných od 0=(00000000) až po 255=(11111111). Co hodnoty znamenají, záleží na konkrétní aplikaci. Především můžeme každý bajt převést do desítkové soustavy a podívat se, jaké číslo vlastně reprezentuje. Náš příklad (10011101) odpovídá číslu 157 – „pravý“ bit opět reprezentuje jednotky, a dále směrem doleva jsou pak zaznamenány další mocniny dvojky. Tam, kde má dvojkový zápis méně než 8 binárních číslovek, ho zleva doplníme nulami, aby byl náš kontejner hezky vyplněn. Takže číslo 3 s dvojkovým zápisem (11) odpovídá bajtu (00000011).

Interpretace bajtů se ale nemusí omezovat na čísla mezi 0 a 255. Pokud pracujete na londýnském OPBH a děláte si zrovna soupis realitních nabídek, „byty“ vám pomohou evidovat volné byty. Ale vážně - bajty mohou stejně dobře jako čísla reprezentovat i obrázky nebo písmenka.

U grafiky se to dělá takto. Každý obrázek se skládá z pixelů - tedy z bodíků na obrazovce. Má-li obrázek rozměry 400x300 pixelů, skládá se vlastně ze 120 000 malých svítivých teček. Na to, abychom jej nějak podchytili, potřebujeme specifikovat, jakou má každý pixel barvu. Pokud nebudeme příliš nároční a vystačíme si s 256 barvami, tak si můžeme udělat tabulku barev, která každému bajtu (tedy číslu mezi 0 a 255) přiřadí jednu konkrétní barvu. Jeden každý pixel pak podle tabulky zaznamenáme jedním bajtem (bajt nám řekne, jakou má příslušný pixel barvu). Všechny barevné pixely pak řádek po řádku - jako když čteme knihu - zaznamenáme někam na disk a hnedle máme obrázek převedený do formátu, který lze v počítači uchovat - jako posloupnost bajtů. V tomto příkladu bychom spotřebovali 120 000 bajtů, neboli 120 kilobajtů, čili 120 kilo, jak říkají ajťáci. Moderní obrázky jsou navíc komprimované, takže ve skutečnosti je těch bajtů potřeba o něco méně. Komprimaci si můžete představit, jako když zedníci zdí řadu cihel. Místo, aby Franta řekl: „Hele, budu potřebovat cihlu, cihlu, cihlu, cihlu, cihlu, překládku, cihlu, cihlu, cihlu, cihlu, cihlu a cihlu,“ tak v rychlosti zahlásí: „Hele, potřebuju pět cihel, překládku a šest cihel". Všimněte si, o co je druhá verze kratší - je totiž komprimovaná!

+++

S textem je to ještě jednodušší. Základem úspěchu je opět tabulka, která nám umožní každému znaku (písmenku, číslici nebo interpunkčnímu znaménku) přiřadit číslo mezi 0 a 255. To potom převedeme do dvojkové soustavy a dostaneme opět jeden bajt (byte), se kterým už si náš počítač lehce poradí. Nejznámější takovou tabulkou je ASCII (tady je i s oktálním a hexadecimálním zápisem). V této tabulce má např. malé „p“ hodnotu 112, malé „e“ 101 a malé „s“ 115. Když si tato tři čísla převedete do dvojkové (binární) soustavy a nalevo je vycpete nulami, aby měly osm pozic, dostanete: „01110000“, „01100101“ a „01110011“. Tyto tři bajty tedy v počítači reprezentují slovo „pes“. Teprve v okamžiku, kdy si otevřete webovou stránku nebo editor, vám počítač ty tři bajty opět zobrazí jako písmenka „p“, „e“ a „s“.

V tabulce ASCII vidíte, že všechna anglická písmenka, číslice i běžné znaky se vešly do rozmezí 0-127. Nabízí se tedy otázka, jaké znaky přiřadit bajtům odpovídajícím číslům 128-255. V internetovém pravěku (tedy kolem roku 2000) počítače moc paměti neměly, a proto byla patrná snaha minimalizovat velikost souborů tím, že se do volného prostoru v tabulce ASCII nastěhovala různá bezprizorní písmenka z jiných jazyků. Západoevropské země si do něj nacpaly různé znaky, které se v anglické abecedě nepoužívají (např. norské „œ“, španělské „ñ“ či francouzské „ç“). Češi rovněž nelenili, když do horní poloviny ASCII vpašovali písmenka s háčky a čárkami, a také Rusové zjistili, že azbuka se do rozmezí pohodlně vejde.

Tím ovšem vznikl velký problém. Zatímco spodní polovina tabulky ASCII (0-127) byla pro celý svět stejná, horní polovinu (128-255) si každý vykládal po svém - někdo jako azbuku, někdo západoevropsky a někdo hezky česky. Aby se to nepopletlo, zavedl se pojem „kódování“, který stanovil, jak se horní polovina tabulky ASCII (tedy de facto bajty začínající jedničkou) má vlastně interpretovat. Jenže zdaleka ne všichni uživatelé byli schopni si kódování správně nastavit, nemluvě o tom, že mnohé programy používaly automaticky nějaké úplně jiné, než uživatel očekával, a tak vznikl písmenkový galimatyáš. Místo abyste se potěšili pohledem na precizně zvládnutou diakritiku, tak se na vás kolikrát z emailu vysypaly nějaké tatarské klikyháky. Navíc japonské či čínské znaky se do horní poloviny ASCII nevešly vůbec.

Naštěstí svět počítačů za posledních dvacet let pokročil rázně technologicky kupředu, takže už nebylo nutné minimalizovat velikost textových souborů „bajtovým“ škudlením. A tak se nakonec internetová rada starších rozhodla, že se rozloučí s myšlenkou „jeden znak, jeden bajt“ a rozšíří tabulku ASCII tak, aby se daly zobrazit i exotičtější písmenkové soustavy. Rozšířená verze se jmenuje Unicode a dokáže obsloužit prakticky všechny velké světové jazyky (a bez překrývání!). Unicode se mimochodem často zapisuje v soustavě šestnáctkové (hexadecimální), ve které je rozmezí pro jeden bajt od „00“ po „ff“, proto při listování tabulkou uvidíte spoustu „divných“ čísel. Lehce si ale spočítáte, že „ff“ skutečně odpovídá desítkovému 255 (občas se místo malých používají velká písmenka, tak se nenechte rozhodit, pokud někde místo „ff“ uvidíte „FF“).

Základní tabulka Unicode obsahuje 65536 znaků, což je 16^4 = 256^2, takže se pohodlně vejde do dvou bajtů. Její znaky se často zapisují ve formě U plus 4 hexadecimální číslovky - např. „U+8CF7“. Dva bajty jsou tedy „8C“ a „F7“. Když si šestnáctkové číslo (8cf7) převedete na desítkové, obdržíte 36087, což je pořadí tohoto znaku v tabulce Unicode. Zde jde o písmenko Han z čínské abecedy.

+++

Skutečnost, že se jeden bajt dá hexadecimálně zapsat v rozmezí „00“ až „ff“, se někdy používá k sofistikovanějšímu kódování barev (v něm ale budeme na každou barvu potřebovat 3 bajty). Každá barva se dá rozložit na červenou (red), zelenou (green) a modrou (blue) komponentu. Tedy dá se namíchat z určitého počtu dílků červené, zelené a modré. Tuto operaci si můžete představit jako matlání barev na paletě. A počet dílků budeme samozřejmě držet mezi 0 a 255, aby se nám vešel do jednoho bajtu. První bajt nám tedy řekne, kolik dílků červené naše barva má, druhý bajt zachytí podíl zelené a třetí modré. Podle anglických názvů barev se tomuto typu záznamu říká „RGB code“.

Například čistá červená obsahuje 255 dílků červené, 0 dílků zelené a 0 dílků modré. Její RGB kód je tedy (255,0,0). Když si tři čísla převedete do hexadecimální (šestnáctkové) soustavy, dostanete FF, 0 a 0 a po doplnění každé komponenty na dva znaky a jejich spojení v kompaktní formát dostaneme výsledný hexadecimální výraz pro červenou jako „FF0000“ (někdy doplněný anglickým znakem pro číslo na „#FF0000“). Mějte na paměti, že tento slepenec vznikl spojením tří hexadecimálních čísel - jedno pro každou barevnou komponentu. Nedívejte se na něj jako na jedno celistvé šestnáctkové číslo.

A opačným směrem to funguje podobně. Pokud chcete rozšifrovat barvu, jejíž hexadecimální „slepenec“ je „#4B761F“, tak si ho nejprve rozřezáte na individuální dvouznakové komponenty: „4B“, „76“, „1F“. Tato šestnáctková čísla si převedete do desítkové soustavy (viz výše) a dostanete: 75, 118 (pozor, i těch „76“ je zapsáno šestnáctkově, takže si musíme i zde udělat přepočet: 7*16 + 6*1 = 118) a 31. Naše barva „#4B761F“ se tedy skládá ze 75 dílků červené,118 dílků zelené a 31 dílků modré.

Při práci s barvami na webu se někdy hodí hexadecimální tabulky. Pokud se vám nějaká barva líbí, ale chtěli byste do ní přikápnout trochu červené, tak prostě první (červenou) komponentu lehce navýšíte. V předchozím příkladu by to mohlo být třeba „#4E761F“ (zde jsem přidal tři dílky červené, tj. zvýšil jsem 75 na 78 a převedl zpět do hexadecimální soustavy).

Článek je redakčně upravenou verzí blogového příspěvku na serveru iDNES.cz. Publikováno s laskavým svolením autora.

Další díly a původní texty jsou dostupné na blogu Jana Řeháčka.

Mohlo by vás také zajímat:

Matykání I: Hudba sfér
Matykání II: Chcete vidět nekonečno?
Matykání III: Jak se dopočítat nekonečna
Matykání IV: Jak se nedopočítat nekonečna
Matykání V: Tajemný svět prvočísel
Matykání VI: Na konečné nekonečné řady
Matykání VII: Moje nekonečno je větší než to tvoje
Matykání VIII: Živočichozpyt číselné osy
Matykání IX: Mají zlomky rodiče?
Matykání X: Jak komunikovat s mimozemšťankami
Matykání XI: Proč má oktáva 12 půltónů?
Matykání XII: Olbersův paradox

Autor: Jan Řeháček