Statistika se může jevit jako skládka bizarních vzorečků, jejichž smyslem je vyextrahovat z lesnických tabulek pravděpodobnost úmrtí chrousta. Základy statistické magie se naštěstí dají pochopit pomocí mechanismu náhodné proměnné.
Hned na začátku musím říci, že lví podíl na špatném renomé statistiky mají někteří horliví kantoři, kteří nebohou číslovědu nekompromisně zavlečou do džungle kombinatorických vzorečků, ve které se jakákoliv myšlenková podstata spolehlivě ztratí v hustém porostu binomických koeficientů. Studenti, místo aby se naučili vyhodnocovat data a rozlišovat statisticky významné trendy od nahodilých, se pak plácají od variací k permutacím, teskně dumají, zda při výběru barevných míčků z osudí záleží na jejich pořadí, a při počítání kombinací se trápí s opakovanými elementy. Ne že by ta trocha myšlenkové disciplíny študákům uškodila, ale smutným výsledkem této drezúry bývá brunátný puberťák, skřípající zubama a snažící se spočítat, jaká je pravděpodobnost, že uhodnete bankovní heslo složené z pěti písmen, dvou čísel a jednoho interpunkčního znaménka, nebo jaká je šance, že v hasičské tombole vyhrajete dva objekty téže barvy. Přitom většina pravděpodobností, se kterými se v praktickém životě setkáme, se nezíská z kombinatorických vzorečků, ale podstatně snadněji z empiricky naměřených dat.
Statistika patří k bouřlivě se rozvíjejícím odvětvím. Informační revoluce je v plném zuřu (schválně kdo pozná, co to znamená), statistické algoritmy se používají v netušené škále od spamovacích filtrů až po google-translate a firmy topící se ve vlastních datech zoufale hledají plavčíky, kteří při pohovoru neomdlí, zaslechnou-li výraz „lineární regrese“. Kdybych mohl dát mladým zájemcům o matematiku jednu radu, řekl bych jim, že pokud si zatím v královně věd nenašli oblíbené hájemství, tak ať se dobře naučí statistiku (zejména bayesovskou analýzu). To jim podstatně usnadní uplatnění na pracovním trhu.
Srdcem statistické analýzy a vstupní branou do jejího křivolakého bludiště je pojem náhodné proměnné, což je jakýsi zásobník, který místo nábojů produkuje statistické údaje (obvykle čísla, ale výjimečně i písmenka či jiné těstoviny).
Zda jsou ty údaje skutečně náhodné, nebo jen pseudonáhodné, a zda je jejich nahodilost způsobena přílišnou komplexitou problému, nedostatečně určenými počátečními podmínkami či svobodnou vůlí nějakého vykutáleného jedince, je z praktického pohledu celkem irelevantní. Tuto filozofickou meditační platformu opatrně překročíme a podíváme se, jak se vlastnosti velmi široké škály souborů dat dají charakterizovat pomocí souhrnných profilů a co všechno se z nich můžeme dozvědět.
Náhodná veličina
V životě se se setkáváme se spoustou kvantit, jejichž výpočet je natolik komplexní, že se na ně můžeme bez uzardění dívat jako na výsledek náhody - nedají se dopředu přesně určit. Počet panen po vyhození deseti mincí do vzduchu, čas potřebný k dojetí do práce, „vytočené“ číslo rulety, HDP Bruneje za rok 2019, první písmenko další zprávy na serveru iDnes atd.

Náhodná proměnná (veličina) je pohodlný zastřešující mechanismus, který nám umožní o těchto kvantitách přemýšlet nějakým sjednocujícím a srozumitelným způsobem. Můžeme si ji opět představit jako skříňku s trpaslíkem, do které bouchneme pěstí, načež trpaslík mručivě zakleje, provede nějaký náhodný úkon (vyhodí deset mincí do vzduchu nebo si půjčí naše auto a dojede s ním do práce) a na výstupu nám naservíruje hodnotu X (počet panen či délku cesty ve vteřinách). A kolikrát do té skříňky bouchneme, tolik hodnot X nám nabídne.
Náhodná veličina trochu připomíná funkce v tom, že generuje číselné hodnoty. Pouze u funkcí je to proces zcela deterministický a průhledný: pokud vložíte stejný vstup, tak se vám na výstupu objeví vždy stejné číslo. Například kulička shozená z výsuvné plošiny dopadne na zem v čase, který závisí pouze na výšce plošiny, a pokud experiment zopakujeme, dostaneme vždy ten samý výsledek.
U náhodných veličin se výstupní hodnota bude naopak vždy trochu lišit (protože vstupních parametrů je většinou moc a nedají se dost dobře kontrolovat). Pokud budeme uvažovat například čas potřebný k dojetí do práce, bude výsledek každé realizace záviset nejen na hustotě provozu a přízni semaforů, ale i na nečekaných jevech, jako je bouračka na trase, objížďka či náhlá průtrž mračen. Já například dojedu do práce většinou za 17-18 minut. Ale už jsem to zajel i za 15 (v noci) a na druhou stranu mi to jednou trvalo 30, když opravovali silnici.
Také značení je trochu jiné. U funkcí se obvykle ptáme, jaká je výstupní hodnota y pro zadané x. U náhodných veličin nás nezajímá ani tak konkrétní hodnota x, která se na výstupu ze skříňky objeví, jako spíš její pravděpodobnost. Tedy jaká je šance, že náhodná veličina X bude mít konkrétní hodnotu x, popř. že bude ležet v intervalu (a, b). To se zapíše pomocí pravděpodobností takto:
P(X=x) pro první možnost a P(a<X<b) pro druhou
(to, že se proměnná jako taková značí velkým X, zatímco její konkrétní číselná hodnota malým x, je trochu matoucí, ale bohužel se to tak používá)
Tak jako funkce popisují procesy deterministické, náhodné proměnné popisují procesy náhodné. A protože není proces jako proces, je těch náhodných proměnných celá řada - zrovna tak jako funkcí. Čísla získaná házením kostkou jsou v principu zcela jiná než ta, která nasbíráte u východu z kina, když se budete vycházejících návštěvníků dotazovat na tělesnou výšku. V prvním případě jsou čísla rovnoměrně rozdělená mezi 1 až 6, zatímco v tom druhém budou některé výšky pravděpodobnější než jiné. Narazit na dámu vysokou 165 cm asi nebude problém. U 180 cm byste se před kinem pěkně načekali...
Mimochodem, v učebnicích se i náhodná veličina často prezentuje jako tradiční funkce, kam se jako vstup strká náhodný jev a na výstupu pak vytéká jeho kvantitativní zhmotnění v podobě reálného čísla. To sebou ale obvykle nese komplikace v podobě teorie míry, a proto se pro potřeby Matykání přidržím jednoduššího popisu. Do skříňky nic házet nebudeme, prostě do ní bouchneme jako do ruské televize a trpaslík už se postará, abychom neodešli s prázdnou.
Náhodná veličina je tedy nástroj, jak zkrotit příval dat do úhledného kap-kap-kap. Z pohledu matematiky je důležité, zda je náhodná proměnná diskrétní (celé číslo či nějaká kategorie, která se na něj dá převést), anebo spojitá, kdy je na výstupu číslo reálné. Diskrétní veličinou může být například den v týdnu, kdy se náhodně vybraný člověk narodí. Spojitou pak bude třeba délka jeho života v sekundách.
Klíčovým pojmem pro pochopení náhodné veličiny je její rozdělení, což je jakýsi přehled všech možných hodnot a jejich četností v daném procesu či datovém souboru (zkrátka v těch číslech, kterými nás trpaslík na požádání zásobuje). Z rozdělení náhodné veličiny velmi rychle poznáme, které hodnoty můžeme čekat častěji a které méně často, a také z něho můžeme vypočítat další zajímavé statistické údaje.
Nejprve se podíváme na příklad diskrétního rozdělení. Představme si, že stojíme někde za městem u poměrně nefrekventované křižovatky a zaznamenáváme si, z kterého směru do ní vjíždí auta. Toto definuje náhodnou veličinu se čtyřmi hodnotami (Sever, Východ, Jih a Západ). Když sečteme výsledky celodenního monitorování, dostaneme souhrnný záznam četností (viz vlevo dole), kterému říkáme histogram náhodné veličiny (do křižovatky vjelo 12 aut ze severu atd.).
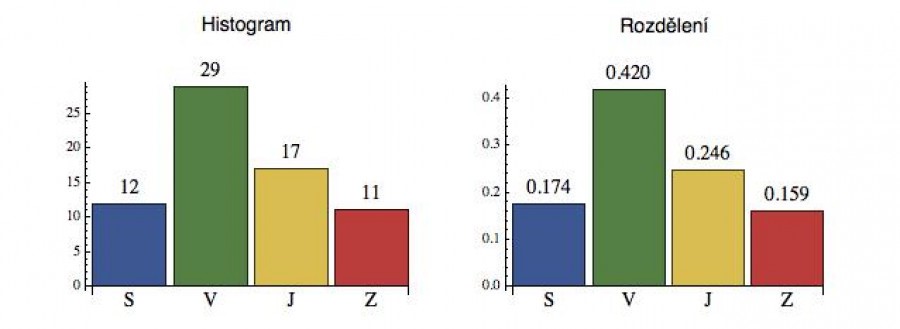
Když si ta čísla v histogramu vydělíme celkovým počtem zaznamenaných vjezdů (69), dostaneme velmi dobrý odhad pravděpodobnosti (na obrázku vpravo), že do křižovatky vjede vozidlo z daného směru. Takto normalizovanému histogramu říkáme rozdělení náhodné veličiny (někdy se slovo „rozdělení“ používá neformálně i jako synonymum pro „náhodnou veličinu“ jako takovou).
Diskrétní náhodná veličina tedy není nic jiného než soubor hodnot s příslušnými pravděpodobnostmi. Ty hodnoty jsou většinou čísla, ale mohou to být i kategorické proměnné (jako právě u tohoto příkladu). To znamená, že v tomto případě nebudeme moci spočítat třeba průměrný směr, ze kterého nám vozidla do křižovatky vjíždí (leda bychom ty nálepky SVJZ přepočítali na úhly), ale na druhou stranu díky empiricky naměřeným pravděpodobnostem můžeme z tabulky odečíst, jaká je šance, že nám do křižovatky vjede vozidlo z jihu (P = 0.246) nebo dvě vozidla ze severu za sebou (P = 0.174*0.174 = 0.03). Žádnou permutací ani kombinací se to spočítat nedá, protože kombinatorika - ani jiná součást matematiky - nemůže tušit, že paní Nováková na severu právě vyštvala svého muže koupit pekařské droždí, takže tento v době našeho pozorování projíždí v plném trysku a zuřu křižovatkou.
Všimněte si, že z toho rozdělení se v žádném případě nedá spočítat, jaká bude další hodnota, kterou nám trpaslík na vstupu naservíruje.
U spojitých veličin je definice náhodné proměnné o něco komplikovanější. Zadáme interval, ze kterého bude trpaslík naše čísla vybírat, a funkci f, která nám umožní počítat pravděpodobnosti (ta funkce je tak trochu spojitým histogramem).
Ale pozor, i když obecně platí, že vyšší funkční hodnoty indikují, že body z tohoto okolí jsou pravděpodobnější, f(x) není přímo pravděpodobnost, že nám trpaslík na výstupu vyhodí bod x (body samy o sobě mají u spojitých rozdělení nulovou pravděpodobnost). Proto se té funkci říká hustota pravděpodobnosti (pravděpodobnost z ní spočítáte podobně, jako počítáte hmotu ze znalosti hustoty - tedy v obecném případě integrací).
Pravděpodobnost, že náhodná veličina X leží v nějakém podintervalu (a, b), je daná plochou pod funkcí f(x) na tomto intervalu. Na dalším obrázku vpravo je to vyznačeno pro podinterval (4, 6) pro funkci definovanou na intervalu (0, 10). Plocha té červené části tedy odpovídá hodnotě
P(4 ≤ X < 6)
U diskrétního rozdělení (obrázek vlevo) by nám pro tutéž pravděpodobnost stačil součet přes hodnoty X splňující uvedenou podmínku: 0.27 + 0.17 = 0.44. U spojitého ty hodnoty, zakódované ve funkci f, musíme integrovat (integrál je spojitou verzí součtu). Ale hrůzu z toho mít nemusíte. V 21. století za vás integraci provede nějaký software - jen mu musíte říci, jaké rozdělení (tedy jakou funkci) uvažujete a odkud kam tu pravděpodobnost chcete spočítat.
Na ose x tedy máme hodnoty naší náhodné proměnné a na ose y jejich pravděpodobnosti (resp. hustotu pravděpodobnosti - v případě spojitém)
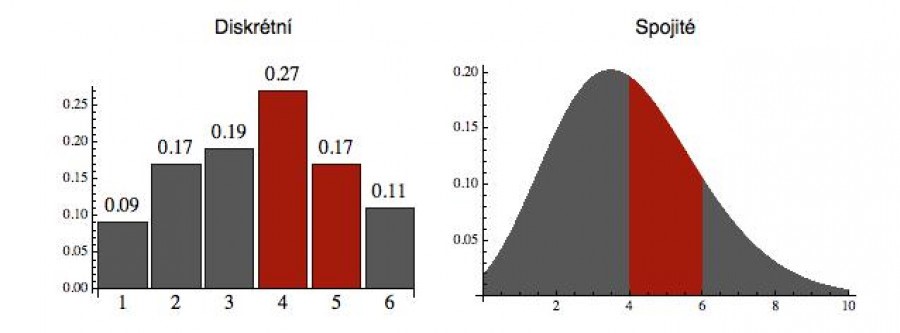
Ještě jednou zdůrazním, že u diskrétního rozdělení může mít jedna konkrétní hodnota (bod) kladnou pravděpodobnost - např. P(X=4) = 0.27. U spojitých je P(X=4) = 0, protože plocha pod křivkou od 4 do 4 je nula. Proto mají body (tj. jednotlivé konkrétní hodnoty) u spojitých rozdělení nulovou pravděpodobnost.
To odpovídá intuitivní představě, že pokud je v osudí konečný počet čísel (třeba 10), tak šance, že si jedno konkrétní vybereme, je nenulová (zde 10 %). Pokud jsou ale v osudí všechna reálná čísla z nějakého intervalu (a mají stejnou šanci tažení), pak je pravděpodobnost, že si vybereme jedno konkrétní - třeba jedničku - nulová (může za to jako obvykle „limita“: vezměte si reálná čísla mezi 0 a 10 a spočítejte si, jaká je pravděpodobnost, že to vámi tažené bude mezi 0,9 a 1,1. Krátký výpočet ukáže, že P(0,9<X<1,1) = 0.2/10. A jak se ten interval kolem jedničky zmenšuje, zmenšuje se i příslušná pravděpodobnost a limitně se blíží nule).
Jen tak ledasjakou křivku si ale pro funkci definující hustotu pravděpodobnosti vybrat nemůžeme. Protože souhrn všech možností nám musí dát stoprocentní jistotu (např. máme stoprocentní jistotu, že při hodu mincí nám padne panna, nebo orel), celková plocha pod křivkou musí být rovna 1 - jednu z hodnot definičního intervalu nám trpaslík prostě vyhodit musí (to platí i pro diskrétní veličinu: když si posčítáte pravděpodobnosti přes všechny možné hodnoty X, musíte taky dostat 1). Pokud daná funkce tuto podmínku nesplňuje, musíme ji nejprve vydělit její celkovou plochou (za předpokladu, že je konečná) a teprve pak můžeme tuto funkci použít pro definici rozdělení. To je také důvod, proč ve funkcích popisujících spojité náhodné proměnné „plavou“ různé normalizační konstanty (ale ruku na srdce: to je pořád lepší, než aby se do těch funkcí dostali normalizační kádři).
Kolik takových funkcí je? Samozřejmě nekonečně mnoho. Naštěstí v praxi se používá jen několik základních typů funkcí, které popisují náhodné jevy, se kterými se v aplikacích setkáváme nejčastěji.
V levé části dalšího obrázku je slavná Gaussova křivka, která popisuje spojité náhodné veličiny, které mají tzv. normální rozdělení (např. výška, IQ, chyba měření). Je to v podstatě kvadratická exponenciála, která v sobě obsahuje dva důležité parametry. Parametr m udává, kde má křivka „střed“ (tedy kde dosahuje maximální hodnoty) a parametr s ukazuje její rozptyl - tedy zhruba řečeno její šířku.
V pravé části je pak tzv. Gamma rozdělení (popisující např. pojistné nároky nebo dešťové srážky), které má také dva parametry (obvykle se jim říká škálový a tvarový parametr) a ty si můžete nastavit tak, aby výsledná hustota pravděpodobnosti co nejlépe popisovala vaši náhodnou veličinu či naměřená data.
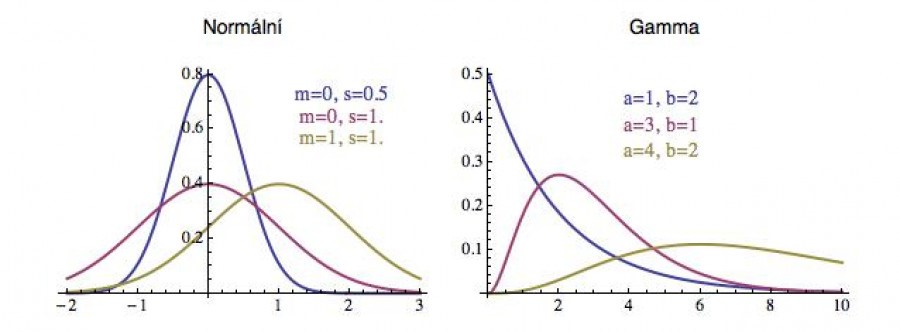
Jak obecně poznat, zda mají experimentálně naměřená data normální, nebo gama rozdělení (nebo nějaké úplně jiné), je poměrně obtížná otázka a často se o ní - pro daná data - vedou spory. Pokud víte, jaký typ rozdělení sledovaný proces má, tak stačí jen dostatečně přesně odhadnout parametry z naměřených dat a máte hustotu doma.
Dobrý statistický software by měl také obsahovat malý program, který dokáže vaše data načíst a udělat z nich solidní odhad té pravděpodobnostní funkce (většinou to dělá tak, že každý datový bodík „obalí“ malou Gaussovu křivku centrovanou v tom bodě, a na konec je všechny posčítá).
Histogram hysterických historiků
Letopočty jsou jako slova. Některé přejdeme téměř bez povšimnutí a nad jinými si s chutí zahysterčíme. Myslím, že byste lehce uhodli, které jsou ty „citlivé“.
Představme si náhodnou veličinu, spočívající v tom, že trpaslík poté, co mu bouchneme do skříňky, odběhne na blog iDnes, vybere si náhodně nějaký článek a z něho si náhodně vybere nějaký letopočet (pokud tam žádný není, tak si vybere jiný článek) a tento nám vyhodí na výstupu. Jaké bude rozdělení této diskrétní náhodné veličiny?
Na následujícím obrázku jsem projel blogy za poslední 4 roky, vycucal z nich všechny letopočty a sestavil jejich histogram (pouze od roku 1900, protože ty starší jsou zmiňovány jen výjimečně).
Z této četnosti (histogramu) bychom pak po vydělení celkovým počtem všech nalezených letopočtů dostali kýžené pravděpodobnostní rozdělení.
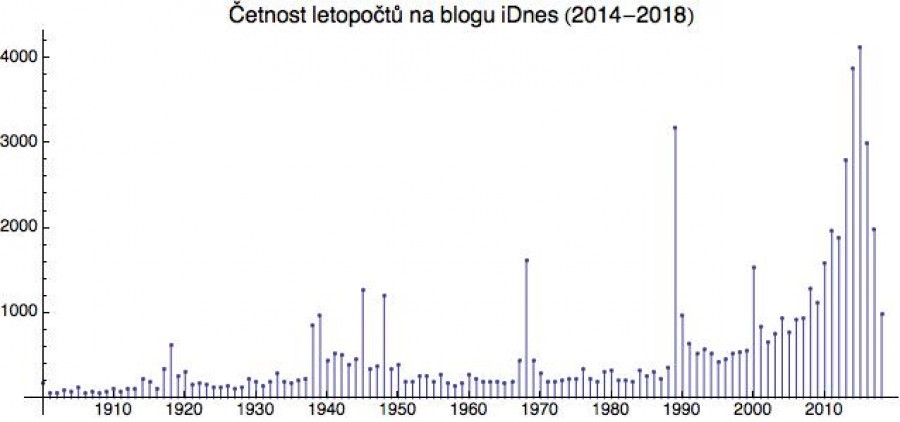
Pod drobnohled jsem si dal letopočet 1968. Když se podíváte na
následující časovou řadu, vidíte, že rok 1968 zmiňujeme obvykle v srpnu. V jiných měsících jsou odkazy poměrně sporadické. Pravděpodobnost
nalezení letopočtu 1968 v blozích je tedy v měsíci srpnu podstatně
vyšší než jindy. Tento postřeh vede ve statistice k zavedení velmi
důležitého pojmu „podmíněná pravděpodobnost“ (ale na ten se
podíváme až někdy v budoucnosti).
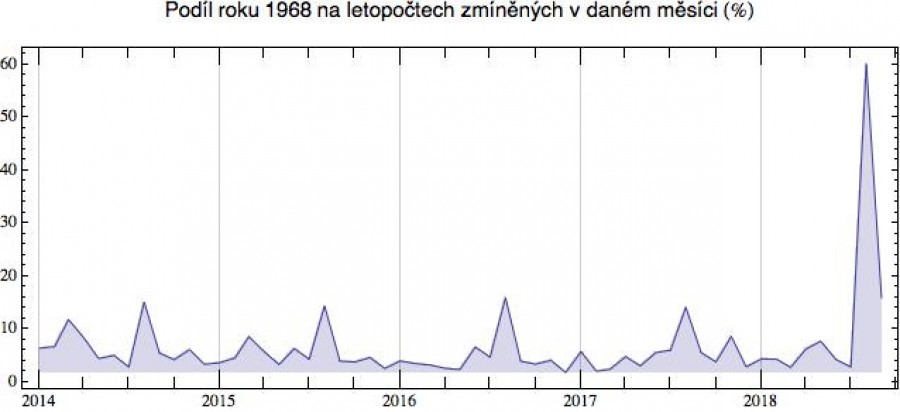
(zajímavý výkmit je v únoru 2014, kdy ruská intervence na Ukrajině zřejmě mnoha blogerům zavdala příčinu k historickým analogiím s rokem 1968)
A když už jsem se pustil do zkoumání blogů iDnes pohledem náhodných veličin, ukážu vám ještě jednu spojitou (nebo spíše kvazispojitou). Je jí karma článku (tj. čtenářské ohodnocení). Ta samozřejmě také článek od článku náhodně kolísá, a když si spočítáte její rozdělení, dostanete následující obrázek (a tady jsem právě použil software, který sám převádí získaná data na pravděpodobnostní funkci a sám se také postará, aby celková plocha pod funkcí byla 1).
>> karma je na ose x, její pravděpodobnost na ose y
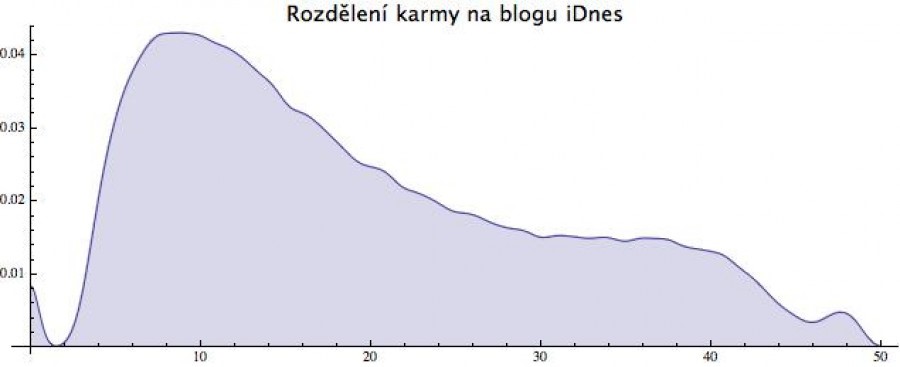
Vidíte z něho, že náhodně vylovený článek bude mít pravděpodobně
karmu kolem 10. Toto rozdělení má dále malý výkmit na začátku,
způsobený tím, že pokud článek propadne (nezíská dostatečný počet
čtenářů), tak mu zůstane karma 0 a jeden (zajímavější)
výkmit na konci, který způsobují články, které se proderou na výsluní
přízně čtenářů (ať třaskavostí tématu, zpracováním či
umístěním v nějakém výběru), a zde pak lehce nasbírají karmu kolem
48.
Když se na tu karmovou funkci podíváte, zjistíte, že trochu připomíná červenou verzi gama rozdělení. Až na ty dva výkmity. Pak bude na vás, zda si jako model pro náhodnou generaci karmy vyberete gama funkci (s tím, že tam bude nějaká ta chybička), nebo budete listovat statistickými příručkami v naději, že objevíte lepší rozdělení, anebo se sami pokusíte tu funkci popsat interpolací.
Důležité je, že pravděpodobnostní funkce představuje určitou signaturu daného procesu. Pokud byste si příští rok zapisovali všechny karmy a na konci roku je opět převedli na náhodnou veličinu, dostali byste skoro určitě velmi podobnou funkci. Tvar té funkce je tedy něco jako statistický otisk prstů, podle něhož můžete náhodný proces často identifikovat.
Pokud mi dáte číslo, řekněme 32.8, a zeptáte se mě, zda je to karma článku na iDnes, anebo aktuální teplota v nějakém světovém městě, tak to samozřejmě nebudu vědět. Možné by bylo obojí. Když mi ale takových čísel dáte milion, tak si z nich nabrnkám hustotu pravděpodobnosti, a pokud bude vypadat jako to nahoře, tak vím, že jste mi dali vzorek karmy, pokud bude jiné, dali jste mi pravděpodobně nějaká teplotní data bůhví odkud.
Tohoto principu se v moderní datové analýze velmi často používá například při strojovém určování entit (např. zda Josef Čapek, zmíněný v nějakém článku, je bývalý slávistický fotbalista, anebo známý malíř) anebo při detekci bankovních podvodů (i naše bankovní či nákupní aktivity mají jistou statistickou signaturu, a pokud se od ní aktuální data příliš liší, může to zvednout varovný praporek).
K čemu je to všechno dobré
Nabízí se samozřejmě otázka, k čemu je taková náhodná veličina dobrá, když z ní konkrétní hodnotu experimentu v reálném životě stejně nevyčteme. Generátor náhodných čísel vám dokáže nagenerovat tiket do loterie, ale navržená čísla se s těmi taženými asi moc shodovat nebudou.
Odpověď je, že někdy tu konkrétní hodnotu ani znát nemusíme a stačí nám, když známe rozdělení příslušné náhodné veličiny (tedy když víme, jaké hodnoty nabývá a s jakými pravděpodobnostmi).
Představte si třeba, že projektujete parkoviště před obchodním domem a potřebujete vědět, na kolik parkovacích míst ho „nadimenzovat“. Když přestřelíte, zbytečně vyplýtváte místo i asfalt, když podstřelíte a kapacita bude příliš malá, zákazníci budou remcat, že musí parkovat v záložních lokalitách. Majitel obchoďáku je ochoten tolerovat nutnost použití záložního prostoru v 5 % případů. Kolik míst tedy naprojektovat?
Náhodnou veličinou X zde bude počet vozidel na srovnatelném parkovišti. Trpaslík tedy na každé bouchnutí vyběhne ven před nějaký podobný obchoďák a spočítá, kolik je na parkovišti zrovna aut. Když nastřádáte dostatečně mnoho dat, můžete si udělat rozdělení této náhodné veličiny (je to diskrétní proměnná, takže dostanete v podstatě histogram) a pak si položit otázku, jaké musí být x aby
P(X < x) = .95
Z následujícího histogramu vidíme, že počet aut na parkovišti kolísá mezi 17 a 43. Ta první hodnota se v souboru dat objevila 1x, poslední 2x, u ostatních to vidíte vždy nad sloupečkem. Pak už ty četnosti pouze převedeme na pravděpodobnosti (vydělíme počtem měření: 500) a začneme odzadu pravděpodobnosti sčítat. Tam, kde dosáhneme 5 %, se zastavíme. To bude počet aut, pro který lze očekávat, že „přetečení parkoviště“ nenastane častěji než v 5 % případů.
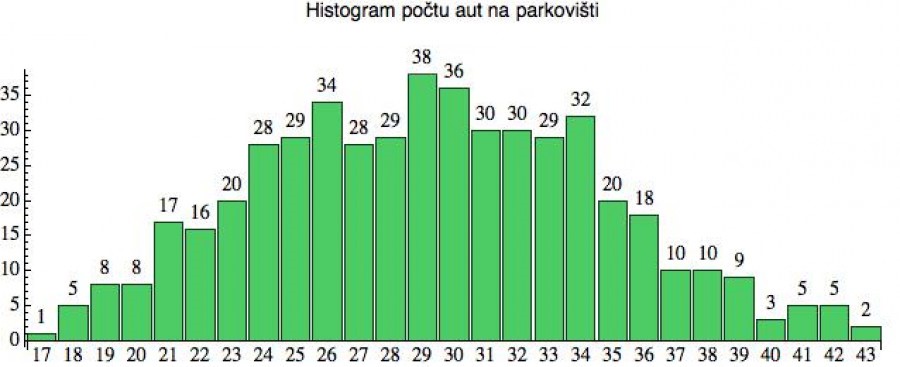
A vlastně to ani na pravděpodobnosti převádět nemusíme. Dá se to určit
přímo z četností. Celkový počet měření je 500, takže z toho 5 % je 25.
Pomalu tedy začneme četnosti (zprava!) sčítat, a jakmile se
dotáhneme na 25, tak skončíme. Takže jedem (zprava): 2 + 5 + 5 + 3
+ 9 = 24 a to je dostatečně blízko. Další člen už by nás hodil přes 25.
Optimální počet míst na parkovišti tedy bude někde kolem 38 (vzhledem k uvedené toleranci).
Všimněte si, že majiteli podniku je srdečně jedno, zda budou jeho zákazníci muset zajíždět na odlehlé parkoviště v dubnu nebo v říjnu, ve středu nebo v sobotu. Jemu jde pouze o to, aby to nebylo častěji než v 5 % případů - a to je něco, co se z toho rozdělení spočítat dá (a doslova na prstech).
(a teď něco složitějšího - pro mimořádně otrlé jedince)
Někdy nastane situace, že byste potřebovali generátor náhodných čísel, který neplive čísla rovnoměrně rozdělená mezi 0 a 1 (což dělá většina generátorů náhodných čísel), ale poskytuje hodnoty, které mají přesně stejné rozdělení jako nějaký reálný proces X (např. momentální venkovní teplota).
Otázka tedy je, jak si obecně nabrnkat generátor náhodných čísel, jehož rozdělení (tedy jeho hustota pravděpodobnosti) bude mít nějaký předem zadaný tvar. Na dalším obrázku vlevo jsem jedno takové rozdělení vyznačil anglickou zkratkou PDF (probability density function). A chceme vyprodukovat čísla, která budou mít přesně takové rozdělení.
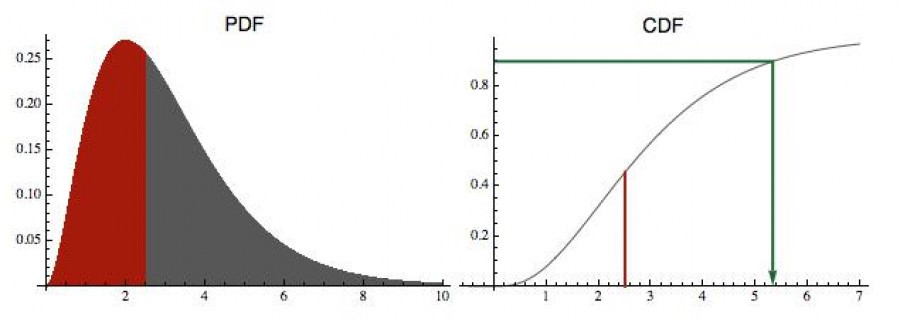
Tento generátor se sestaví pomocí tzv. distribuční funkce, na obrázku
označené CDF (cumulative
distribution function). Ta je pro dané x definovaná jako plocha pod PDF od
minus nekonečna až po x. Neboli pravděpodobnost, že náhodná veličina tou
PDF určená je menší než x.
CDF(x) = P(X<x) = plocha pod PDF nalevo od x
V našem případě má náhodná veličina pouze kladné hodnoty, takže plochu (naakumulovanou pravděpodobnost) začínáme de facto počítat od bodu 0. A pro každé x tuto hodnotu vyneseme do grafu funkce CDF. V pravé části obrázku je to pro x = 2.5 vyznačeno červenou úsečkou. Velikost odpovídající červené plochy z levé části obrázku je tedy zhruba 0,45. Protože celková plocha pod PDF je 1 (je to hustota pravděpodobnosti), musí ta CDF směrem doprava konvergovat k 1.
Tak a teď vlastní postup: náhodně si vyberete číslo z intervalu (0, 1) - to většina programovacích jazyků umí - nanesete ho na osu y a z grafu funkce CDF pak odečtete hodnotu x, která se do tohoto čísla zobrazí (viz zelená šipečka). Na obrázku mi standardní generátor vybral z jednotkového intervalu číslo 0.9 a tomu odpovídá na ose x hodnota zhruba 5,28. A to bude jedno z čísel, které mi nový generátor („ušitý“ na rozdělení odpovídající předložené PDF) nabídne. Jinými slovy: vyberete si rovnoměrně y z intervalu (0, 1), zelenou šipečkou mu najdete partnera na ose x a toto číslo vyhodíte na výstupu. Rozdělení této náhodné veličiny vám přesně vytvoří tu křivku na předchozím obrázku nalevo. Když si to rozmyslíte, tak vlastně používáme inverzní funkci k té kumulativní CDF (z hodnoty y určujeme hodnotu x).
Proč to funguje? Protože CDF je de facto integrálem té PDF (počítá naakumulovanou plochu). Tam, kde je funkce PDF „vysoká“ (kde jsou nejpravděpodobnější hodnoty naší náhodné veličiny), tam její plocha poroste nejrychleji, takže CDF (vpravo) bude mít pro tyto hodnoty x velkou derivaci (poroste strmě). A když se podíváte, jak z toho intervalu (0, 1) na ose y náhodně „střílíte“ ty zelené zalomené šipečky na osu x, tak je jasné, že největší šanci „zasáhnout“ křivku CDF mají právě v místech vysokého růstu (kde je ta CDF křivka strmá, respektive ta PDF křivka vysoká). Je to stejný princip, jaký do nás kdysi hustili při vojenské přípravě: je daleko snazší zasáhnout vzpřímeného vojáka než ležícího.
Mimochodem, specializovaný statistický software většinou umí ta nejznámější rozdělení opět vygenerovat sám, takže vám tuto práci ušetří.
Purista by mohl namítnout, že náhodná čísla, která mají rozdělení jako ta PDF z předchozího obrázku, vlastně zase tak úplně náhodná nejsou, protože se nejčastěji „motají“ kolem hodnoty 2. Pokud vás to irituje, můžete jim klidně říkat „skoro náhodná“. Faktem je, že úplně čirá náhodnost, kdy je rozdělení rovnoměrné, a příslušná rozdělovací funkce (PDF) je de facto konstantní, se v přírodě zase tak často nevyskytuje. Realistická data jsou většinou kombinací pevně daných zákonitostí a přimísené náhody. Proto je taky v tom normálním rozdělení parametr zahrnující šířku Gaussovy křivky. Čím více nahodilosti v datech máte, tím bude křivka širší (o tom více příště, kdy se podíváme na průměry a rozptyly náhodných veličin).
Sekce jauvajs: Binomické rozdělení
V minulém Matykání jsem používal náhodnou veličinu spočívající v tom, že trpaslík vyhodí N mincí do vzduchu a po dopadu spočítá, kolik mu padlo panen. Toto je diskrétní náhodná proměnná k, která může nabývat hodnot 0 až N (více než N panen nám jistě nepadne). Ten počet panen k ale není rozdělen rovnoměrně. Některé hodnoty jsou pravděpodobnější než jiné. V tabulce napravo, vidíte možné hodnoty k a jejich pravděpodobnosti P pro N =10.
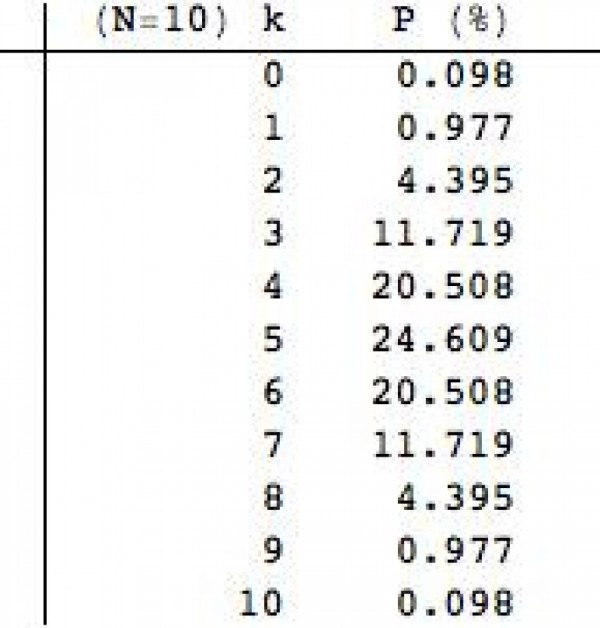
Jak asi očekáváte, nejpravděpodobnější je, že vám padne pět panen.
Čtyři nebo šest už je méně pravděpodobná varianta a nula nebo deset je
téměř vyloučeno, což odpovídá naší reálné zkušenosti.
Tento typ náhodné veličiny je speciálním příkladem tzv. binomického rozdělení, které spočívá v provedení N pokusů (např. hod korunou), jejichž výsledkem je buď „úspěch“ (panna), anebo „neúspěch“ (orel). Nic jiného se stát nemůže. Za předpokladu, že pravděpodobnost „úspěchu“ je p a pravděpodobnost neúspěchu q (kde q = 1-p), tak pro pravděpodobnost dosažení k „úspěchů“ v N pokusech dostaneme binomický vzoreček:
P(X=k) = B(N,k) * p^k * q^(N-k)
Pokud máme k úspěchů, tak musíme mít N-k neúspěchů, což vysvětluje poslední dva členy. Jejich pravděpodobnosti je nutno pronásobit (jsou to nezávislé jevy). Ten první, nejdůležitější, člen odráží skutečnost, že k úspěchů se může vyskytnout kdekoliv mezi N pokusy. Číslo B(N,k) se jmenuje binomický koeficient (popř. kombinační číslo) a ukazuje nám, kolika způsoby můžeme z N pokusů vybrat k „úspěchů“ (v angličtině se proto tento symbol často čte „N choose k“, zatímco v češtině převládá výslovnost „N nad k“).
Jeho definice je celkem známá:
B(N,k) = N! / k! * (N-k)! = N*(N-1)*...(N-k+1) / 1*2*...*k
příklad: B(5,2) = 5*4 / 2 = 10
Tedy vybrat dva „úspěchy“ z pěti pokusů lze deseti způsoby. Ten první úspěch může nastat kdekoliv mezi pěti pokusy, zatímco na druhý už zbývají jen čtyři možnosti. Závěrečné vydělení dvěma je proto, že ty „úspěchy“ se mohou prohodit (obecně je tam permutace k prvků).
Binomické koeficienty možná znáte i ze slavného Pascalova trojúhelníku anebo z binomické věty - tedy z rozvoje výrazu (x+y)^n.
A teď už si úvodní tabulku můžete ověřit sami. V našem konkrétním
případě (hod korunou) je p = q = 0.5, takže pro pravděpodobnost, že nám
padnou k = 3 panny z N = 10 hodů, dostaneme:
B(10,3) * 0.5^3 * 0.5^7 = 120 * 0.5^10 = 0.117188... (skoro 12 %)
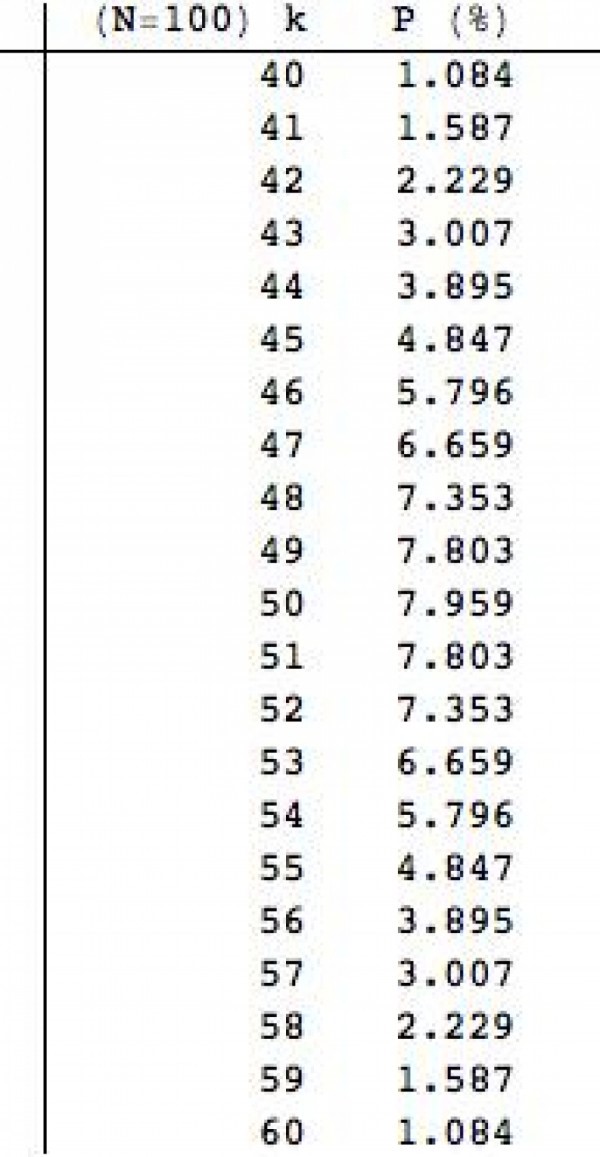
Pokud zvedneme počet házených mincí na N = 100, dostaneme jako nejpravděpodobnější počet panen k = 50 (tabulka vlevo). Tady už je možností neúrekom, a proto je ta nejvyšší pravděpodobnost o něco menší, aby se dostalo i na ostatní „káčka“.
Když si sečtete pravděpodobnosti v první tabulce pro k = 4, 5, 6 (což je 40 až 60 procent z celkového počtu hodů), dostanete cca 65 %. Když si ten samý propočet uděláte pro N = 100, tedy sečtete všechny pravděpodobnosti od k = 40 do k = 60, dostanete podstatně vyšší číslo - cca 96 %.
A to bylo smyslem první části minulého Matykání. Čím více mincemi házíte, tím je těžší pro celkový počet panen dostat se mimo nějaký procentuálně definovaný interval kolem středové hodnoty.
Článek je redakčně upravenou verzí blogového příspěvku na serveru
iDNES.cz. Publikováno s laskavým svolením autora.
Další díly a původní texty jsou dostupné na blogu Jana Řeháčka.




