Kdybych měl ukázat prstem na jednu matematickou disciplínu, jejíž vytrvalé ignorování má nejzhoubnější politické důsledky, byla by to statistika. Bez ní jsme vydáni napospas demagogickým argumentům obratných propagandistů.
Ten říká to a ten zas tohle a všichni dohromady kecáme až moc. Číst v dnešní době noviny není zážitek pro slabé nátury. Žijeme ve světě plném komplexních procesů s mnoha vstupy a výstupy. Z neustálého propojování příčin a důsledků postupně vznikla chaotická motanice akcí a reakcí a jediný způsob, jak se z toho bludiště proudů a protiproudů nezbláznit a z běsnícího moře událostí vylovit jakés takés zdání pořádku, je podívat se na něj prizmatem statistiky.
Takový náhled probíhá ve dvou rovinách. V rovině pravděpodobnostní se rozloučíme se starým viděním světa jako struktury vybudované na jistotách a smíříme se s tím, že většina netriviálních mechanismů, se kterými se v životě setkáváme, má náhodný charakter a že nejpřesnější informace, kterou z nich můžeme vyždímat, je pravděpodobnost, že věci dopadnou tak, jak očekáváme. Nemáme jistotu, že zítra bude pršet, ale je tu 35% šance, že bude. Nemáme jistotu, že nás vezmou na vysokou, ale na 80 % to dopadne. Nemáme jistotu, že si před odjezdem na dovolenou nevyvrtneme kotník, ale na 99 % se nám tato nepříjemnost vyhne. Pravdě se tedy podobá prakticky všechno, ale různou měrou.
V rovině statistické zase opustíme ne zcela reálnou představu, že se nám podaří plně pochopit běh světa, skládajícího se ze sedmi miliard racionálních i iracionálních bytostí, a místo abychom studovali chování jedné každé z nich a snažili se z nich vydedukovat schémata sociálních zákonitostí, soustředíme se na chování společnosti jako celku a budeme sledovat pouze její základní charakteristiky a zprůměrované ukazatele. Ty se dají předvídat lépe a úspěšněji než individuální hodnoty. Tímto směrem se kdysi vydala i statistická fyzika, když při zkoumání termodynamiky zjistila, že nemá smysl (je to výpočetně nezvladatelné) monitorovat polohy a rychlosti každé jednotlivé částečky srážející se s ostatními molekulami v klokotající polévce, a místo toho se pustila do popisu makroukazatelů, jako jsou teplota nebo tlak.
Moderní doba nás zaplavuje přívalovým deštěm vjemů a postřehů, které je potřeba roztřídit a posléze z nich vylouhovat nějaké smysluplné závěry. Internet se stal obrovským úložištěm informací a statistika je jedním z mála nástrojů, kterými lze tuto kolosální masu smysluplně zkrotit. A že toho v ní je. Od záznamů obchodních transakcí přes geografická data až po indikátory sentimentu, jimiž dnem i nocí zaplavujeme diskusní fóra.
Ovšem ne vždy se to louhování obejde bez společenských rizik. Firmy sledují své zákazníky, vlády sledují své občany, a jak ukázal skandál kolem firmy Cambridge Analytica (která vysávala uživatelské informace z Facebooku, aby je pak obratem ruky používala pro politickou analýzu) i pro sběr dat platí stará osvědčená zásada - všeho s mírou. Já se ale nebudu zabývat právní stránkou věci a omezím se na matematiku.
Statistika je všude kolem nás. Zpravodajství nám neoznamují, co na zákaz kouření říká ten nebo ten, ale naservírují nám rozložení názorů podle demografické šablony. Sadaři si postěžují, kolik procent meruněk jim letos pomrzlo, nikoliv které konkrétní stromy se odebraly na věčnost. Televizní reklamy vám přijdou střelené, protože nejsou cílené na vás, inteligentního čtenáře, ale na průměrného spotřebitele. A když se váš počítač setká s neznámým jazykem, nezavolá do filologického ústavu, aby rychle poslali odborníka, ale rozloží nalezený text na po sobě následující dvojice písmen (takže třeba „text“ se rozpadne ne „te“, „ex“ a „xt“), ty spočítá a vzniklé proporce porovná se statistickými profily jednotlivých jazyků (v češtině například prakticky nenajdete oblíbené anglické „th“ nebo „wh“, zatímco v angličtině se zase nedaří v češtině běžným dvojicím jako „zd“ nebo „vl“).
Přesto se mnoho matematiků - o laické veřejnosti ani nemluvě - dívá na statistiku trochu úkosem. Pro ně je to jenom taková kuchařka, jak z daných datových ingrediencí uvařit více méně stravitelnou polévku. Nicméně pro mladé talenty v sobě skrývá obrovské pole pro aplikace. A pokud bude informační revoluce alespoň z poloviny tak úspěšná jako ta industriální, mohou se čerství absolventi statistických oborů těšit na tisíce nových pracovních příležitostí.
Co je statistika
Představte si, že stojíte u fotbalového hřiště, na kterém dva fotbalisté, slavný Lionel Messi a méně slavný Franta Koudelka, právě trénují střely do růžku branky (lidově „do vinglu“). Jejich bilance je pomocí průmětů do roviny branky vyznačena na obrázku níže.
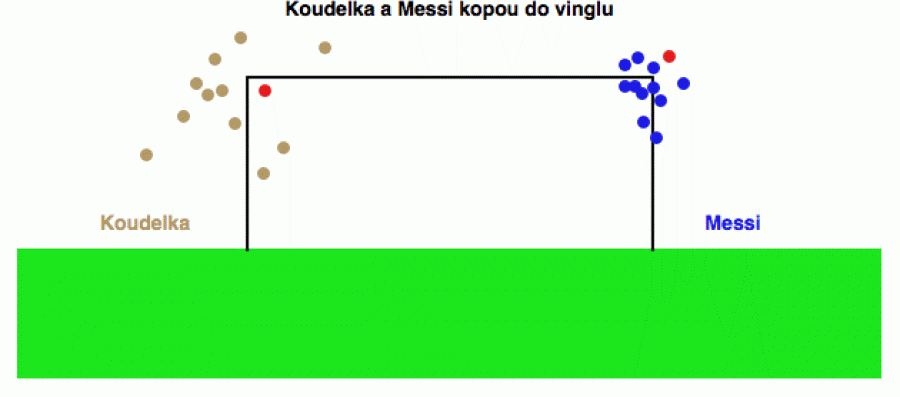
Právě v okamžiku, kdy oba fotbalisté kopou „červenou sérii“, jede
kolem pozorovatel, pan Všetečka, který sice fotbalu nerozumí, ale později v hospodě se rád podělí o své pozorování: „Chlapi, ten náš Franta
Koudelka to zavěsil jak profík, to je pane fotbalista! Ale ten nekopa Messi
byl úplně mimo, ten by byl i zadarmo drahej.“
Připadá vám to za vlasy přitažené? V internetových diskusích se s takovým zkratkovitým uvažováním můžeme setkat každý den. Někdo narazí na hodného uprchlíka a hned vytroubí do světa ódu na multikulti. Někdo narazí na uprchlíka zlého a rázem je z něho promovaný xenofob honoris kauza. Jenže každé naše pozorování je jen střípkem celkové mozaiky a bez znalosti ostatních kamínků nemá žádný smysl vyvozovat z naší izolované zkušenosti jakékoliv závěry. To, že tenhle migrant je doktor a tamhle ten jen pasáček koz, není podstatné. To, co by nás mělo zajímat je, jaká procenta z nich jsou lidé slušní, vzdělaní, charakterní a pracovití, a jak se tato procenta vztahují k charakteristikám převládající populace. To rozhodne o tom, zda jejich příchod bude přínosem nebo ne.
Problém spočívá v tom, že změřit tyto charakteristiky v celé sledované skupině, je prakticky nemožné, a tak se volky nevolky musíme uchýlit k odebrání vzorků. A to je věda sama o sobě, protože ne vždy se podaří namixovat je dostatečně reprezentativním způsobem. To je, jako by k nám z vesmíru dorazili Marťani, zašli si na ženský basketbalový zápas a přímým pozorováním hráček a diváků dospěli k závěru, že na Zemi jsou ženy vyšší než muži. Se vzorky musí člověk (i Marťan) nakládat velmi opatrně.
Zjednodušeně řečeno, statistika funguje na třech úrovních.
1. Ta nejzákladnější spočívá v prostém spočítání výsledků a tu známe všichni z praktického života. Koudelka dal tři góly (z toho jeden do vinglu), Messi dal čtyři a z nich tři do růžku. V této formě konzumujeme povolební statistiky, přehledy vzdělanosti jednotlivých národů nebo údaje o nakažení lišek vzteklinou. K rozklíčování informací nám zde bohatě postačí základní škola.
2. Na vyšší úrovni, které se říká deskriptivní statistika, se snažíme z daných dat vyextrahovat další užitečné informace o jejich povaze, například kde mají střed (těžiště), zda jsou symetrická nebo zda se dají vygenerovat některým ze standardních statistických procesů. Na obrázku nahoře například vidíme, že Koudelkovy pokusy mají podstatně větší rozptyl než Messiho, protože Franta nemá svou kopací techniku tak jemně vybroušenou. Tyto dodatečné informace nám umožňují lépe pochopit, jak se daný datový soubor chová a co od něho lze očekávat.
3. Prediktivní statistika se pak snaží využít obdržené údaje k předpovědím o chování systému. Pokud bychom například získali další vzorek „vinglových“ kopů našich protagonistů, mohli bychom porovnáním s výše uvedenými daty zjistit, zda pochází od Messiho nebo od Koudelky. Takto funguje třeba již zmíněná detekce jazyků. Výsledkem samozřejmě není odpověď typu ano-ne, ale pravděpodobnostní odhad: „tak tento text bude na 90 % švédština, na 75 % norština a na 25 % dánština“.
Jak jsem již poznamenal výše, o vlastnostech daného systému nerozhoduje jedno pozorování nebo jeden jediný vzorek. Důležité je chování celého souboru za delší časový interval. To, že to Messimu jednou nebo dvakrát ulítne, nic neznamená - koneckonců je to taky jenom člověk. Jeho talent se projeví v tom, že pokud těch kopů bude sto, Messi z nich dá 60 vinglů, zatímco Koudelka jenom 20.
Na tom je mimochodem založeno pojišťovnictví. Určité třídy řidičů (podle věku, vzdělání atd.) mají určité dispozice k zapříčinění nehod - i když se v každé skupině najdou individua, která jezdí jako makotřask. Úkolem pojišťováků je zjistit statistické profily jednotlivých tříd a podle zjištěných rizik pak nastavit výši pojistného. Pokud máte takové a takové charakteristiky, pravděpodobnost nehody bude X.
A takto funguje většina komplikovanějších životních situací. Představme si třeba dva kandidáty na pozici manažera ve dvou různých firmách. Pan Lukáš je poměrně dobře připravený a má i delší praxi, ale při pohovoru měl smůlu - předseda přijímací komise se zrovna špatně vyspal a Lukáš vyletěl. Na druhé straně pan Mirek přípravu trochu odflákl a ani jeho praxe zatím není postačující, ale měl kliku. Jeho „předseda“ byl ten den v dobrém rozmaru a Mirka přijal. Jeden výsledek nám samozřejmě o kvalitách Lukáše a Mirka nic neříká (stejně jako jedna série kopů nic nevypovídá o fotbalových kvalitách pana Messiho nebo Koudelky). Teprve kdybychom je oba nechali podstoupit 100 přijímacích řízení, uviděli bychom, že Lukáš je v nich o něco úspěšnější (ovšem v životě těch 100 přijímacích řízení obvykle nepodstupujeme, a proto je důležité mít na své straně - kromě praxe a dovedností - i paní Štěstěnu).
Proto je statistika hnacím motorem dvou důležitých společenských mechanismů: demokratických voleb a volného trhu. Každý máme nějaký názor na směřování společnosti. Někdo by chtěl nižší daně a někdo vyšší. Někdo by chtěl otevřené hranice a někdo zavřené na petlici (a obehnané ostnatým drátem). Jak ale najít uspokojivé řešení, když máme každý jinou osobní zkušenost a jiný názor? V průběhu historie se ukázalo, že nejbezpečnější variantou je obvykle ta, kterou podporuje většina dané populace. Je to tak trochu jako dotaz na publikum v soutěžní hře „Chcete být milionářem“. Ne každý v tom publiku dané otázce rozumí a je schopen ji správně zodpovědět, ale protože chybné názory jsou většinou náhodně a rovnoměrně rozdělené mezi čtyři nabízené možnosti, ten správný názor od informované části publika statisticky převáží, byť třeba jen o fous.
Volný trh funguje na podobném principu. Budou zítra akcie Microsoftu obchodovat na vyšší cenové hladině nebo na nižší? Každý máme jinou zkušenost a jiné očekávání. Někdo má důvody myslet si, že Microsoft se už přežil, a vsadí si na pokles. Někdo se naopak domnívá, že Microsoft své produkty úspěšně inovoval a bude spíše nakupovat. O tom, která tendence nakonec převládne a kudy se cena akcií začne ubírat, rozhodne statistika.
Samozřejmě ani demokracie, ani trh nepředstavují bezchybný mechanismus. V obou případech se najdou mazaní jedinci, kteří se statistiku pokusí podrýt a přesvědčit své spoluhráče, že to jak vidí skutečnost právě oni, je směrodatné. A v obou případech skutečně dochází k manipulacím. I demokratické procesy občas navedou na přistávací dráhu historie začínajícího diktátora a i ve volném trhu dochází ke vzniku nekontrolovatelných bublin. Ale lepší mechanismus, jak řídit komplexní socio-ekonomické procesy, jsme zatím neobjevili.
Co je pravděpodobnost
Pravděpodobnost nějakého náhodného jevu je číslo mezi nulou a jedničkou, které vyjadřuje šanci, že se zmíněný náhodný jev skutečně realizuje (někdy se také udává v procentech - tedy jako číslo mezi 0 % a 100 %). Nula znamená nemožné, jednička jisté. Stejně jako většina objektů v matematice, náhodné jevy mohou být buď diskrétní (hod kostkou či korunou), a nebo spojité (hod šipkou na terč - zde je realizací bod uvnitř kružnice ohraničující terč). Ty diskrétní obvykle počítáme, ty spojité měříme.
Ze školy si připomeneme, že pravděpodobnost je počet (míra) realizací, které vedou k našemu jevu, vydělený počtem (mírou) všech možných realizací. Tedy ve zkratce: počet příznivých možností dělený počtem všech možností. Klasickým případem je hod kostkou. Pokud náš jev A bude spočívat v tom, že nám padne pětka, bude jeho pravděpodobnost rovna P(A) = 1/6, protože existuje šest možných realizací hodu, z nichž k našemu jevu vede jediná: padne nám 5. To samozřejmě neznamená, že každý šestý hod bude pětka. Ale pokud tou kostkou budeme házet celý večer, zhruba šestina z nich skutečně budou pětky (to „zhruba“ je tam proto, že skutečná definice počítá s limitou pro nekonečný počet hodů).
Výpočet si můžeme usnadnit některým ze vzorečků, kterými se pravděpodobnost řídí. Nebudu je zde vyčítat všechny, ale zmíním tři nejznámější.
1. Pokud máme dva komplementární jevy A, A' (tedy alespoň jeden z nich musí nastat), pak součet jejich pravděpodobností je jedna: P(A) + P(A') = 1. Je-li pravděpodobnost, že zítra bude pršet 25%, pak pravděpodobnost, že zítra pršet nebude je 75 %. Ale pozor, to neznamená, že s tou samou pravděpodobností bude svítit sluníčko. Pršet a nepršet jsou komplementární jevy (jeden z nich jistě nastane), déšť a sluníčko nikoliv: klidně může nepršet i nebýt slunečno.
2. Pokud máme dva jevy A a B, které sice nejsou komplementární (opačné), ale vzájemně se vylučují, pak pravděpodobnost, že nastane alespoň jeden z nich, je rovna součtu: P(A nebo B) = P(A) + P(B). Takže pravděpodobnost, že nám na kostce padne číslo menší než 3, si složíme ze dvou jevů: A (padne nám 1) a B (padne nám 2). Takže P(A nebo B) = P(A) + P(B) = 1/6 + 1/6 = 1/3.
3. Pro dva nezávislé jevy A, B pak platí, že pravděpodobnost jejich současné realizace je rovna součinu: P(A a současně B) = P(A) * P(B). Tedy pravděpodobnost, že nám padne pětka dvakrát za sebou je P(A a B) = (1/6) * (1/6) = 1/36. Nebo je-li pravděpodobnost, že naše učitelka bude blondýna 20%, a pravděpodobnost, že bude hubatá 40%, pak pravděpodobnost, že ve škole narazíme na hubatou blondýnu bude 8% (0.2 x 0.4 = 0.08).
Hlouběji se do teorie pravděpodobnosti pouštět nebudu, ale spočítáme si na závěr dva příklady pro diskrétní i spojité jevy, aby bylo lépe vidět, jak tahle habaďůra funguje.
Jednoduchý příklad diskrétní
Jaká je pravděpodobnost, že nám při hodu dvěma kostkami padne součet 9?
Protože obě kostky mají 6 stran, je počet všech možností (jmenovatel) roven 6 * 6 = 36. Ne všechny jsou ovšem příznivé našemu jevu. Realizace dvojhodu, které nám dají součet 9, jsou tyto čtyři: 3 + 6, 4 + 5, 5 + 4 a 6 + 3. Žádná jiná možnost neexistuje, takže výsledná pravděpodobnost bude 4/36 = 1/9.
Než se s kostkami rozloučíme, chtěl bych se zmínit o jednom zdánlivém klamu. Protože pravděpodobnost, že hodíme šestku (jev A), je 1/6, mohli bychom propadnout dojmu, že pokud hodíme kostkou šestkrát, bude pravděpodobnost, že uvidíme alespoň jednu šestku rovna 1, tedy jistota. Ale tak jednoduché to není, pravděpodobnosti se nedají takto bezostyšně násobit (ještě lépe je to vidět na hodu korunou - tam je pravděpodobnost, že nám padne orel 1/2, takže by se mohlo zdát, že stačí hodit dvakrát a alespoň jeden orel nám padne - z vlastní zkušenosti ale víme, že to není pravda).
Pro výpočet bude vhodné přejít ke komplementárnímu jevu A'. Je jednodušší spočítat, jaká je pravděpodobnost, že v šesti hodech neuvidíme žádnou šestku. Ta je pro jeden hod rovna 5/6, a protože hody jsou nezávislé (to, co nám padne, není závislé na výsledku předchozích hodů), dostaneme P(A') = (5/6)^6 = 5^6/6^6 = 15625/46656, což je bratru 0.335. No a pro žádanou pravděpodobnost P(A) dostaneme z komplementárního vztahu: P(A) = 1 - P(A') = 0.665. Takže to, že v šesti hodech uvidíme alespoň jednu šestku, je sice docela pravděpodobné (66.5 %), ale zdaleka ne jisté. Dobře si to rozmyslete.
Složitější příklad diskrétní
Pozveme-li si na večírek N přátel, jaká je pravděpodobnost, že alespoň dva z nich budou mít stejné narozeniny?
Toto je problém úzce spojený se známým paradoxem narozenin, který říká, že stačí, aby se večírku účastnilo 23 lidí, a pravděpodobnost, že dva z nich budou mít stejné narozeniny, překročí 50 % (počet 23 je menší, než by se nám intuitivně mohlo zdát, proto paradox). A teď k výpočtu. Stejně jako v předchozím případě si vypomůžeme komplementárním jevem. Tedy jaká je pravděpodobnost, že mezi N přáteli budou mít všichni rozdílné narozeniny.
Na to se můžeme dívat tak, že každý z účastníků večírku si přinese číslo mezi 1 a 365 a ptáme se, jaká je pravděpodobnost P(A), že dva z N účastníků budou mít stejné číslo, respektive (v té komplementární formulaci), jaká je pravděpodobnost P(A'), že si všech N účastníků přinese různá čísla.
Pokud si to dobře rozmyslíte, dospějete pro P(A') k tomuto výsledku:
(365/365) * (364/365) * (363/365) * (362/365) *...
kde první závorka reprezentuje prvního účastníka, druhá druhého a tak dále až dospějeme k N členům. Každý z účastníků má celkem 365 možností, a proto mají všichni v čitateli 365. Aby ovšem měli různá vybraná čísla (narozeniny), budeme jim muset začít zmenšovat jmenovatele. První účastník si může vybrat číslo, jaké chce - tedy má 365 možností příznivých jevu A'. Ten druhý (pokud chce být v souladu s jevem A') má ovšem možností pouze 364 (nesmí si vybrat číslo, které si vybral první účastník). No a třetí účastník už má k dispozici pouze 363 možností, čtvrtý 362 atd.
Takže pro konkrétní N si snadno spočítáme, jaká je ta komplementární pravděpodobnost. Např. pro N = 5 účastníků dostaneme:
P(A') = (365/365) * (364/365) * (363/365) * (362/365) * (361/365) = 0.972864
a tím pádem pro jev původní nám vyjde
P(A) = 1 - P(A') = 0.0271356
Tedy pro 5 lidí je pravděpodobnost společných narozenin zhruba 2.7 %. To je dost málo. Ale když si budete postupně navyšovat N, pravděpodobnost utěšeně poroste, a pro N = 23 (kdy ve vzorečku budete mít 23 součinitelů) vám P(A) poprvé překročí hranici 50 % (pro N = 22 budete mít pouze 47.5 %).
Kdo tomu nevěří, může si zkusit interaktivní příklad zde.
Jednoduchý příklad spojitý
Představme si, že stojíme na rotující plošině (rotoped), v ruce máme revolver a míříme na 30centimetrový balonek vzdálený od plošiny 5 metrů. Pak nám někdo zaváže oči, roztočí nás a my v náhodném okamžiku stiskneme spoušť. Jaká je pravděpodobnost, že zasáhneme balonek?
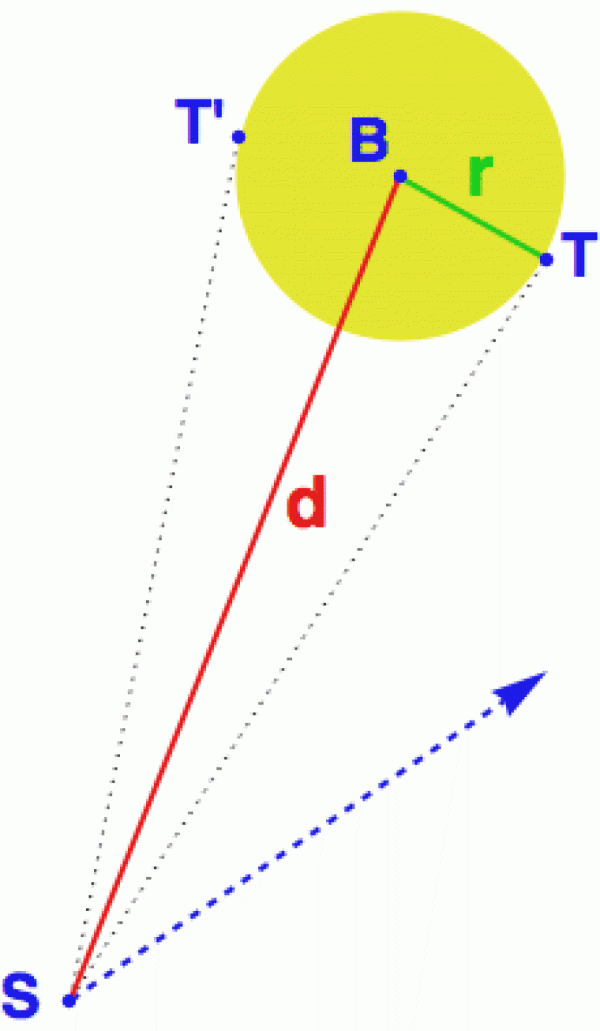
Když si to rozmyslíme, naše náhodně vyslaná střela pohybující se po modré trajektorii zasáhne balonek právě tehdy, pokud se vejde do úhlu TST'. Používáme tedy stejnou metodu, jen místo vypočítávání různých variant je budeme měřit. V čitateli dostaneme 360 stupňů (to je míra všech možných směrových variant našeho revolveru) a ve jmenovateli se nám objeví úhel TST' (ve stupních), který odpovídá směrům, pro které revolver balonek zasáhne.
No a zbytek už je celkem jednoduchá geometrie.
Trojúhelník TSB má pravý úhel v bodě T (tam je vytečkovaná tečna kolmá na poloměr), takže z goniometrických funkcí zjistíme snadno úhel BST (který je polovinou hledaného úhlu).
sin(BST) = r/d = .3/5 = .06
tím pádem úhel nám vychází nějakých 3.44°. Jeho dvojnásobek vydělíme 360° a máme hledanou pravděpodobnost
P = 6.88/360 = 0.019
Šance na zásah (1.9 %) je tedy mizivá, nikoliv však astronomická.
Složitější příklad spojitý
Představte si, že Křemílek s Vochomůrkou nalezli fotbalový míč a neviditelným inkoustem si na něm každý (zcela nezávisle) vyznačil jeden bod. Jaká je pravděpodobnost, že tyto dva body budou ve středu míče svírat pravý úhel?

Především si musíme dát nějakou toleranci na pravý úhel, jinak bude pravděpodobnost nula. U spojitých veličin je totiž - na rozdíl od těch diskrétních - prakticky nemožné náhodně „trefit“ přesnou hodnotu. U hrací kostky vám klidně padne přesně 5 s nenulovou pravděpodobností 1/6. Ve spojitém případě je to složitější. Když si třeba na číselné ose vyberete náhodně bod, řekněme mezi 0 a 1, tak pravděpodobnost, že to bude přesně 0.203 - nebo jakákoliv jiná konkrétní hodnota - je nula (abyste dostali nenulovou pravděpodobnost, tak byste se museli „trefovat“ do nějakého intervalu). Ze stejného důvodu by byla pravděpodobnost v tom předchozím příkladu nula, pokud byste balonek nahradili bezrozměrným bodem. Ten prostě netrefíte.
Takže si dejme toleranci 1° a ptejme se, jaká je šance, že úhel sevřený ve středu sféry dvěma náhodně vybranými body P a Q leží v rozmezí 89° a 91°.
Na kouli se nejlépe pracuje se „zeměpisnými“ souřadnicemi, tj. s délkou a šířkou, a protože sféra je objekt zcela symetrický, umístíme severní pól do bodu P a zeměpisnou šířku budeme počítat „obráceně“ - tedy na pólu bude 0°, zatímco na rovníku bude kýžených 90° (na dalším obrázku je tato šířka vyznačena jako t).
Teď už jenom na tu sféru (s bodem P na severním pólu) umístíme další bod Q a budeme se ptát, jaká je pravděpodobnost, že tento leží velmi blízko rovníku (aby jeho „obrácená“ zeměpisná šířka byla mezi 89° a 91°).
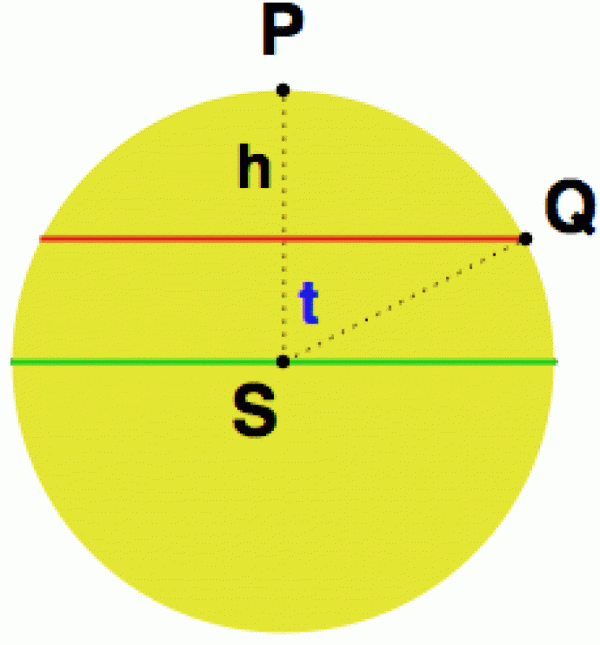
Ze symetrie stačí uvažovat pouze dění na severní polokouli a spočítat, jaká je pravděpodobnost, že se bod Q ocitne v „nudličce“ podél rovníku mezi 89° a 90° (na obrázku vpravo si ji můžete představit takto: bod Q posunete, aby jeho úhel t byl 89° a pak to bude přesně ta oblast mezi červenou rovnoběžkou a zeleným rovníkem).
Hledaná pravděpodobnost teď bude poměr mezi plochou této „nudličky“ (kam se bod Q musí trefit, aby byl „téměř kolmý“ k P) a celkovou plochou severní polokoule. Plochu nudličky získáme tak, že od povrchu severní polokoule odečteme plochu kulového vrchlíku nad příslušnou rovnoběžkou odpovídající t = 89°.
Nalistujeme si tedy vzoreček pro plochu kulového vrchlíku X = 2π r h = 2 π r2 (1-cos(t)), kde t je naše „obrácená“ šířka, a můžeme počítat. Plocha polokoule je Y = 2π r2, takže podílem X/Y bude hodnota 1-cos(t). Protože nás ale nezajímá, kdy bude bod Q v tom vrchlíku, ale kdy bude mimo - tedy v nudličce pod ním - přejdeme opět k doplňku (komplementu) a dostaneme P(A) = 1-X/Y = cos(t) a tato pravděpodobnost má pro t = 89° hodnotu 0.0174524.
Takže šance, že ty dva body budou ve středu S svírat pravý úhel (s tolerancí 1°), bude cca 1.745 %.
Tento zdánlivě nesmyslný problém jsem si vybral proto, že jeho řešení závisí podstatným způsobem na dimenzi koule. Ve dvourozměrném případě (kružnice) je délka kruhového oblouku přímo úměrná úhlu ve středu S, takže odpovídající pravděpodobnost (kdy si Křemílek s Vochomůrkou vybírají bod na kružnici) bude prostě 1/90, což je cca 1.11 % (tedy o něco méně než v 3D případě). Naopak pro vícerozměrné koule (tzv. hypersféry) se pravděpodobnost bude zvyšovat a pro kouli, řekněme, stodimenzionální už bude hraničit s jistotou (tedy 100 %). To souvisí s tím, že v mnoharozměrných prostorech jsou dva náhodně vybrané vektory téměř vždy prakticky kolmé (a k tomu se časem vrátím podrobněji).
Článek je redakčně upravenou verzí blogového příspěvku na serveru
iDNES.cz. Publikováno s laskavým svolením autora.
Další díly a původní texty jsou dostupné na blogu Jana Řeháčka.




