V období internetu by se mohlo zdát, že čísla jsou jen jakési obvody, které si „vegetí“ v kalkulačce a popíjejí střídavý elektrický proud. Kdepak. Čísla jsou velmi zajímavá zvířátka a ve skutečnosti bydlí na číselné ose v Praze 9.
Čísla jsou krví matematiky. Jsou olejem promazávajícím její komplikované soustrojí. A hrnou se na nás doslova ze všech stran. Fyzika, ekonomie, zeměměřičství, statistika a další kvantitativní disciplíny nás každý den zaplavují numerickými informacemi. Ať už je to silniční vzdálenost do Bojkovic ke strejdovi, váha štědrovečerního kapra, souřadnice zlatého pokladu na mapě, výše hrubých národních důchodů nebo vzájemná přitažlivost dvou nebeských těles, jeden každý údaj odpovídá jednomu konkrétnímu desetinnému číslu (technicky reálnému číslu). A aby se všechna ta čísla navzájem nepomíchala, matematici jim vytvořili úhlednou ubytovnu v podobě číselné osy. Najdeme ji na Proseku ve Vysočanské ulici. Anebo v učebnici aritmetiky pro 6. třídu. Teď nevím.
Nejdříve si ale řekněme, co to vlastně číslo je. Představte si, že si v řeznictví poručíte čtyřicet deka krkovičky. Paní šlehne nacvičeným forhendem flákotu na váhu a na digitálním displeji se rozsvítí údaj 403 g. To samo o sobě není ještě váha našeho nákupu. Ta krkovička s největší pravděpodobností neváží přesně 403 gramů. Váha údaje zaokrouhluje, takže její skutečná hmotnost je někde mezi 402,5 a 403,5 g. Na číselné ose proto té hmotnosti ještě neodpovídá bod, ale interval (tedy kousíček číselné osy „vocuď pocuď“). Samozřejmě bychom si mohli půjčit atomové váhy odvedle z laborky a zjistit, že krkovička váží 402,91179 gramů, ale ani to ještě není přesná váha, i když příslušný interval, ve kterém leží, už by byl podstatně užší. Teprve když bychom použili posloupnost přesnějších a přesnějších vah, tak bychom se nakonec dobrali ke zcela přesné hodnotě, vyjádřitelné číslem s nekonečným desetinným rozvojem.
Číslo je tedy jakási idealizovaná hodnota určité kvantity a na číselné ose jí odpovídá jeden jediný bod. Ten bod má pochopitelně nulovou délku, což znamená, že danou kvantitu vystihuje zcela přesně. Zda ji umíme či neumíme prakticky změřit, je něco, s čím si matematik hlavu neláme. Takové světské starosti přenechává fyzikům a inženýrům. Když si matematik usmyslí, že dostane přesně pí kilo bůčku (π = 3,141592...), tak ho prostě dostane, i kdyby musel jet do řeznictví na druhém konci města. A kdyby ho náhodou bylo o ždibíček víc, tak se jednoduše kousíčíčíček masa odkrojí, aby ho zůstalo přesně pí kilo.
Pokud fandíte moderní fyzice, tak se teď asi nad tou naivní představou trochu mračíte. Hmota se přece nedá libovolně dělit – v jistém okamžiku se dostanete na úroveň atomů a tam se přihozením dalšího atomu bůčku už dostanete „nad váhu“. A odebrat jen tak čtvrtinu atomu dost dobře nemůžete. Zda jsou reálná čísla pro náš fyzikální svět skutečně dobrým modelem, je zajímavá otázka a někdy v budoucnosti jí věnuji zvláštní příspěvek. On ten svět totiž není ani zdaleka tak spojitý, jak jsme si ještě před sto lety mysleli. Pro teď ale budeme předstírat, že známe pouze klasickou fyziku, že jakákoliv veličina se dá spojitě zmenšovat i zvětšovat a že takové zlotřilosti jako atomy, kvanta energie či Planckovy délky vůbec neexistují. A teď už k tématu.
Číselná osa
Mnoho studentů si číselnou osu představuje jako krupicovou polévku, ve které jsou jednotlivá desetinná čísla nasypaná bez ladu a skladu jako zrnka krupice. To sice není úplně špatná představa a pro mnohé účely je postačující, ale o něco lepší je představovat si číselnou osu jako rybu na talíři. Když ji nožem podélně rozkrojíte a vidličkou nadzvednete, uvidíte uvnitř kostřičku obklopenou masem - a to je zhruba představa, kterou byste si z tohoto článku měli odnést.
Ve škole do dětí hustí celou taxonomii různých typů čísel, ale podle mého soudu bude stačit, když si zapamatujete, že reálná čísla (lidověji desetinná) se dělí na čísla racionální (zlomky) a iracionální (vše ostatní). Racionální čísla tvoří kostru číselného systému a čísla iracionální jsou potom to maso, které je ke kostřičce přirostlé.
Na obrázku níže jsem racionální čísla vyznačil modře a iracionální červeně. Kdo má odvahu a zdá se mu takové dělení příliš hrubé, může si z čísel racionálních oddělit jako speciální skupinu čísla celá (tmavomodrá) a z čísel iracionálních čísla algebraická (světle červená). Čísla celá asi znáte, a pokud přijmete hru na rozkrojenou rybu, můžete jim přisoudit roli páteře. Iracionální algebraická jsou čísla, která se sice nedají zapsat jako zlomky, ale dají se pořád z celých čísel vyždímat vyřešením nějaké celočíselné polynomiální rovnice vyššího stupně (kvadratická, kubická atd.). Typickým představitelem takového algebraického čísla je odmocnina ze dvou (1,41421356...), která je řešením celočíselné kvadratické rovnice:
x² - 2 = 0
Protože čísla algebraická mají ke zlomkům poměrně blízko (i zlomky jsou mimochodem algebraická čísla, protože jsou řešením lineárních rovnic s celými čísly), můžete si je v naší hře představit jako chrupavku. Takže sečteno a podtrženo, v následujícím schématu uvidíte páteř (celá čísla), kostru (racionální čísla), chrupavku (algebraická iracionální čísla) a maso (tedy zbytek iracionálních čísel, kterým se říká čísla transcendentní).

Tento diagram znázorňuje skutečnost, že celá čísla jsou součástí
zlomků a zlomky jsou součástí algebraických čísel. Transcendentní
čísla, jak vidíte, stojí trochu stranou – jsou to takoví psanci
číselné osy. Možná si při pohledu na obrázek říkáte, zda by nebylo
lepší dělit reálná čísla na algebraická a transcendentní. Upřímně
řečeno, spousta matematiků se na to tak dívá – a mají pro to dobrý
důvod – ale protože naším konečným cílem bude v příštím díle
struktura racionálních čísel, přidržím se původního modro-červeného
dělení na zlomky a nezlomky.
Ty čtyři typy čísel se samozřejmě na číselné ose neshlukují, ale jsou mezi sebou rozptýlena. Jinými slovy jsou hezky multikulturně promíchané. Celou osu si pak můžete představit jako kolekci bodíků obarvených podle výše vyjmenovaných typů. Příklad vidíte na dalším obrázku.
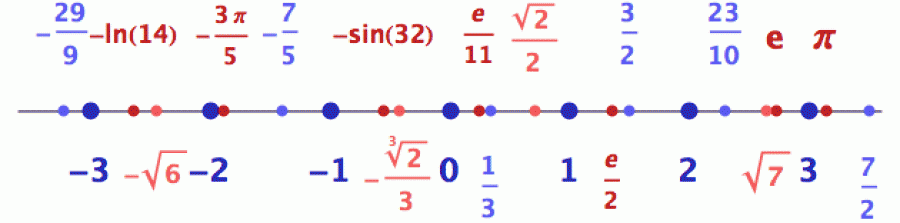
O tom, jak dokonale jsou racionální a iracionální čísla promíchaná,
svědčí i následující tvrzení: mezi každými dvěma racionálními
čísly existuje alespoň jedno iracionální a naopak – mezi každými dvěma
iracionálními čísly existuje alespoň jedno racionální. Pokud si to
chcete za domácí úkol dokázat, uvažte, že „pí krát zlomek“ je vždy
iracionální číslo (ale pozor, není to úplně jednoduchý důkaz).
Všechna čísla na obrázku jsou označena pomocí matematických symbolů. Takto zapsaná čísla se však obtížně porovnávají, protože algebraický zápis vám neřekne, zda je číslo ln(7) větší nebo menší než třeba 22/7. Proto má každé reálné číslo také svůj standardní desetinný zápis, např: 2 = 2,000..., 1/3 = 0,3333..., ln(7) = 1,94591... atd. Takové hodnoty se porovnávají daleko lépe. A zda si pro zápis toho kterého čísla vyberete desetinný rozvoj, nebo nějaký algebraický symbol, který vyjadřuje funkci toho čísla v číselném systému, je většinou na vás. V reálu je to stále ta samá hodnota – ať už ji zapisujete standardním desetinným číslem nebo nějakou funkční formulkou. Je to podobné jako když někdo tomu muži v Bílém domě říká „prezident USA“ (funkční zápis) a někdo jiný prostě Donald Trump (standardní zápis). Ale v realitě je to stále jeden a tentýž chlap.
Trocha historie
Poměrně dlouhou dobu se zdálo, že si matematika vystačí s čísly racionálními (zlomky), protože ta dokázala spolehlivě pokrýt všechny praktické výpočetní potřeby. Jejich užitečnost se – z pohledu moderní analýzy – zakládá na dvou vzájemně souvisejících vlastnostech.
1. Racionální čísla jsou v číselné ose hustě rozložená. To znamená, že ať si vezmete jakkoliv malý kousíček reálné osy – třeba interval od 0,147 do 0,148 – tak v něm nějaké racionální číslo vždy najdete (dokonce se dá ukázat, že jich v něm najdete nekonečně mnoho). To si můžete představit takto: Oba konce si napíšete jako zlomky – 147/1000 a 148/1000. Jejich aritmetický průměr je také zlomek a musí nutně ležet uvnitř toho intervalu (leží dokonce přesně v polovině). Toto tvrzení platí, i pokud se oba konce intervalu jako zlomky napsat nedají, jen je ta konstrukce pak o něco zapařenější.
2. Každé reálné číslo se dá s libovolnou přesností aproximovat racionálním číslem. To vyplývá z faktu, že každé desetinné číslo s konečným počtem míst je v podstatě zlomek. Například Ludolfovo číslo se dá postupně aproximovat těmito zlomky (se stále větší přesností):
3,1 = 31/10
3,14 = 314/100
3,141 = 3141/1000
3,1415 = 31415/10000
3,14159 = 314159/100000 atd.
Tyto dvě vlastnosti, spolu se skutečností, že v racionálních číslech (zlomcích) můžeme bez uzardění provádět všechny běžné aritmetické operace, přivedly lidstvo k názoru, že žádná jiná čísla vlastně ani neexistují. Nejsou potřeba. Všechny vlastnosti našeho vesmíru se (zdánlivě) dají popsat zlomky. Nemůžeme se proto divit, že ještě staří pythagorejci, kteří si libovali v estetice, byli formální harmonií zlomků zcela unešení, a když se jeden z nich jménem Hippasos domákl, že existují i iracionální čísla, tak ho kolegové ze zhrzené profesionální cti utopili (i když pravděpodobnější verze asi bude, že se roztěkaný Hippasos utopil sám). Svět se pythagorejcům musel jevit jako dobře seřízený hodinový strojek a ten darebák Hippasos se opovážil do útrob toho božsky tikajícího zařízení vhodit starý šroubovák.
Ještě horší bylo, že iracionální číslo, které Hippasos objevil, nebylo nějakou šílenou abstrakcí učedníkovy choré mysli, nad kterou by Pythagorova družina mohla pohrdavě mávnout rukou. Naopak, bylo to zcela legitimní a veskrze praktické číslo – konkrétně velikost úhlopříčky v jednotkovém čtverci. Když si ji spočítáte pomocí Pythagorovy věty (ta ironie!), dostanete sqrt(2), tedy odmocninu ze dvou.
+++
Podívejme se teď na klasický důkaz, že toto číslo se skutečně jako zlomek napsat nedá. Je to víceméně důkaz sporem, nic kromobyčejně těžkého. Předpokládejme tedy pro spor, že se číslo sqrt(2) dá zapsat jako zlomek, to znamená, že se dají najít dvě celá čísla M a N splňující rovnici:
sqrt(2) = M / N
Dále předpokládejme, že tento zlomek už je v základním tvaru, tedy že čísla M a N nemají žádné společné dělitele (pokud by nějaké měly, tak je prostě vykrátíme a dostaneme zlomek v základním tvaru, např. 4/6 = 2/3). Když celou rovnici vynásobíme N a umocníme ji na druhou, dostaneme:
2 N2 = M2
Je jasné, že číslo M2 je sudé (je to dvojnásobek celého čísla N2), a tudíž i samo číslo M musí být sudé (rozmyslete si proč). To znamená, že pravá strana je dělitelná 4 (sudé číslo na druhou je vždy dělitelné 4). Pak ale musí být levá strana také dělitelná 4. A z toho plyne, že N nemůže být liché číslo, protože pak by i N2 bylo liché číslo a dvojnásobek lichého čísla není nikdy dělitelný 4. My však víme, že levá strana dělitelná 4 je. Takže N je také sudé. Jenže jsou-li jak M, tak N sudá čísla, pak mají společného dělitele – konkrétně dvojku – a to je ve sporu s naším tučně vytištěným předpokladem v předchozím odstavci. Žádná taková čísla M a N tedy existovat nemohou a odmocnina ze dvou se nedá zapsat jako zlomek. Je to číslo iracionální. První v historii lidské civilizace.
+++
A od této chvíle to šlo s racionálními čísly z kopce. Postupně se ukázalo, že iracionálních čísel je nejen nekonečně mnoho, ale je jich dokonce nespočetně mnoho (viz minulé Matykání). Přesto však stále považujeme racionální čísla za kostru našeho číselného systému a jak ta kostra konkrétně vypadá, si ukážeme příště.
A teď budeme muset pár století přeskočit.
Zatímco o existenci iracionálních čísel věděli už ve starém Řecku, o transcendentních číslech se poprvé zmiňuje až Leibniz v roce 1682 a jejich moderní definici vypiloval o něco později Euler. Transcendentní čísla reprezentují kvantity, které se nedají odvodit z celých čísel pomocí algebraických rovnic. Jsou to objekty často zahalené rouškou tajemnosti a obecně se dá říci, že ukázat transcendentnost nějakého čísla je podstatně těžší než dokázat jeho iracionalitu.
Pro ilustraci se můžeme podívat na známé číslo π (3,14159..). Pokud máte rádi kuriozity, můžete si nejdřív prohlédnout první milión čísel jeho desetinného rozvoje. Iracionálnost Ludolfova čísla ukázal švýcarský matematik Johann Lambert už v roce 1761. Jeho transcendence si však musela na rigorózní důkaz počkat až do roku 1882, kdy jej publikoval německý matematik Ferdinand von Lindemann. Se základem přirozených logaritmů, tedy s číslem e (2,71828..) je to obdobné. Jeho iracionálnost odvodil švýcarský matematik Leonard Euler už v roce 1737, zatímco jeho transcendenci dokázal až francouzský matematik Charles Hermite v roce 1873.
Tím však nechci říci, že dokázat iracionalitu nějakého konkrétního čísla je v 21. století brnkačka. V předminulém Matykání jsme viděli, že stále existují poměrně důležitá čísla, o kterých to neumíme dokázat ani dnes – například hodnota Riemannovy funkce zeta v bodě 5 (desetinný rozvoj tohoto čísla je zhruba 1,036927755...) nebo tzv. Eulerova konstanta (0,5772156649...). Takže i na číselné ose má světová matematika ještě více než dost práce.
Článek je redakčně upravenou verzí blogového příspěvku na serveru
iDNES.cz. Publikováno s laskavým svolením autora.
Další díly a původní texty jsou dostupné na blogu Jana Řeháčka.




