Vlastní čísla mají spoustu zajímavých aplikací. Jednou z těch méně známých je použití spektrální analýzy pro zkoumání struktury sociálních sítí (a společenských interakcí obecně). Jejich matematickým popisem se zabývá teorie grafů.
V poslední době sílí hlasy poukazující na rozdělenou společnost. Pamatuji doby, kdy člověk s jiným politickým názorem byl prostě – a teď se podržte – člověk s jiným politickým názorem. I s takovým bylo možné zajít do hospody, na tenisový kurt či do přírody. Ale s nástupem fenoménu „polarizace“ jako by se něco podstatného zlomilo. Lidé s odlišnými názory jsou najednou nepřátelé, se kterými je nutno rázně zatočit, a ne chodit do hospody. A to není jen problém české kotliny. Velmi markantní to bylo během amerických voleb, kdy vášně cloumaly celým kontinentem.
Nehodlám tento fenomén pitvat sociologicky nebo dokonce politicky. Kdybychom se měli dobrat jeho občanských příčin, byli bychom tu do rána. V tomto Matykání se soustředím pouze na jednu metodu, která nám umožní celou situaci nějak kvantifikovat. A protože jednotlivci spolu komunikují (a tedy vyměňují si informace) převážně prostřednictvím sociálních sítí – ať už virtuálních či reálných – základním matematickým nástrojem nám bude teorie grafů, tedy disciplína zkoumající propojení individuálních elementů z dané množiny.
Reprezentační graf populace se bude skládat jednak z jednotlivců (těm budu říkat vrcholy grafu) a jednak z jejich interakcí (těm budu říkat hrany grafu). Aby se nám to matematicky nezašmodrchalo, vrcholy grafu označím přirozenými čísly – nebudu tedy říkat „vrchol Novák“, „vrchol Svoboda“ nebo dokonce „vrchol drzosti“, ale vrchol_1 či vrchol_2. Počet vrcholů bude n.
Hrany pak budou reprezentovat neuspořádané dvojice vrcholů (tj. dvojice čísel 1... n). V našem případě budou indikovat jakousi sociální „spřízněnost“. Tedy bude-li v našem grafu hrana_12, znamená to, že vrchol_1 se kamarádí s vrcholem_2. Počet hran se obvykle značí písmenkem m.
Jak se spřízněnost konkrétně realizuje, je z pohledu matematiky irrelevantní. Můžete si ji představovat jako udělování plus v diskusích, lajkování na Facebooku anebo jako výsledek nějakého dotazníku, jehož cílem bylo zjistit přátele či spojence v dané komunitě.
Podívejme se nyní na sérii 3 grafů, kde vrcholy reprezentují členy nějaké komunity (diskutéři, obyvatelé městečka atd.) a hrany reprezentují jejich spřízněnost, tedy kdo s kým vlastně „mluví“.
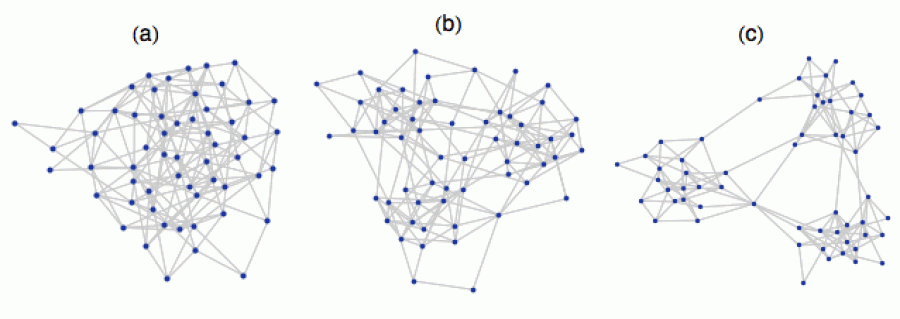
Na levém obrázku je idealizovaná (a v praxi asi nedosažitelná) situace, kdy je komunikace vedena napříč všemi složkami společnosti a lidé spolu „kamarádí“ zcela homogenně. Na prostředním obrázku už je patrná určitá diferenciace, kdy se lidé nesdružují zcela náhodně, ale tvoří určité komunity, ať už profesní, zájmové či politické. Takový graf je v podstatě realistickým popisem situace. Společenské vztahy nejsou determinované náhodným vrhem kostky, ale odrážejí určitou strukturu. V pravé části je pak extrémní verze tohoto mechanismu: zde je společnost viditelně rozdělená do „sociálních bublin“, které mezi sebou komunikují spíše sporadicky.
Samozřejmě v případě malých grafů stačí mrknout na obrázek a hned je jasno, zda je společnost kompaktní či roztříštěná. U velkých grafů (s tisícovkami vrcholů) už to tak jasné není. Proto bychom rádi definovali nějaké číslo, které nám ukáže, kde se na škále „kompaktnost–roztříštěnost“ daná populace vlastně nachází. Ono i u těch menších grafů je někdy užitečné mít k dispozici konkrétní číslo, které reálnou situaci ocení, abychom se nemuseli spoléhat na své „baj voko“. Například máme-li časovou posloupnost grafů a chceme vědět, zda se roztříštěnost zvyšuje či snižuje.
Každý graf je určen množinou svých vrcholů a hran:
G = G(V,H), kde V jsou vrcholy a H hrany
(v angličtině je to G(V,E), kde V jsou „vertices“ a E „edges“)
Klíčem k úspěchu bude následující postřeh. Jedním z důsledků existence sociálních bublin je zpomalování šíření informace. Pokud v levém grafu někomu něco řeknete a on to okamžitě vyzvoní všem svým sousedům v grafu (tedy těm, se kterými je spojen hranami), za chvíli bude novinku vědět celá vesnice.
V pravém grafu to tak jednoduché není. Novinka se poměrně rychle rozšíří pouze v rámci bubliny, do které byla vypuštěna, ale do ostatních bublin informace prosákne podstatně pomaleji, protože mezi jednotlivými komunitami neexistuje dostatek komunikátorů.
Rychlost šíření informace v grafu se dá odhadnout z jeho struktury. A naopak, známe-li rychlost šíření, můžeme z toho něco o struktuře grafu usoudit. A to bude základním kamenem dnešního Matykání.
Toto jednoduché pozorování zpracujeme matematicky ve třech fázích:
1. Naučíme se šíření nějaké substance po grafu (ať už je to informace nebo pytel cukru) popsat pomocí matic, které nám umožní na problém nasadit dobře propracovaný aparát lineární algebry.
2. Pomocí vlastních čísel odhadneme „rychlost šíření“ v grafu a z toho odvodíme míru polarizace dané komunity.
3. Pomocí vlastních vektorů se naučíme posoudit roli jednotlivých vrcholů při šíření či nešíření dané substance. To nám umožní nejen určit obrysy komunit, ale také rozlišit mezi těmi, kdo sedí zarytě uprostřed svých sociálních bublin a těmi, kdo komunikují i přes valy vystavěných barikád.
Celé této proceduře se říká „spektrální shlukování“ (spectral clustering) a my se teď na tyto tři fáze podíváme podrobněji.
1. Co s maticemi?
Nejprve pár slov o tom, jak grafy nějak rozumně matematicky uchopit.
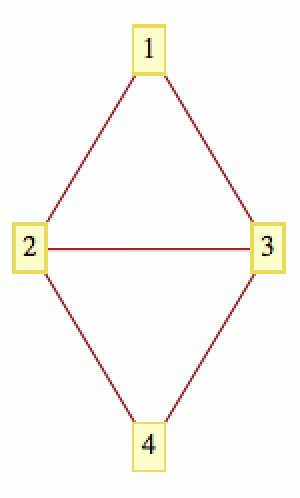
Pro spoustu praktických výpočtů můžeme graf zakódovat pomocí seznamu „sousedů“ (zde je ukázka v jazyce Python, jak se pak takový seznam používá). Pro každý vrchol v∈V prostě vypíšeme vrcholy, se kterými je v spojen hranou. Pro graf na obrázku vpravo dostaneme:
1 --> {2,3}
2 --> {1,3,4}
3 --> {1,2,4}
4 --> {2,3}
Protože ale budeme hojně využívat lineární algebru, vypomůžeme si dalším populárním nástrojem pro popis grafů, a to je tzv. „matice sousedství“ (adjacency matrix). Pro daný graf G(V,H) ji budu značit A a v té nejjednodušší podobě indikuje, které dvojice vrcholů (i,j) jsou spojeny hranou.
A(i,j) = 1, pokud (i,j)∈H, tedy pokud existuje hrana mezi vrcholy i a j
A(i,j) = 0, pokud taková hrana neexistuje (vrcholy i a j nejsou spojeny)
Pro výše uvedený graf bude mít matice A tvar:
A = ((0,1,1,0),(1,0,1,1),(1,1,0,1),(0,1,1,0))
(v komplikovanějším případě můžeme jedničky nahradit „váhami“
jednotlivých hran)
Všechny grafy v tomto Matykání budou neorientované (to znamená, že hrana mezi vrcholy i a j nemá „směr“). Pokud je i sousedem j, je také j sousedem i. Matice A je v tomto případě symetrická, neboť splňuje A(i,j) = A(j,i).
Občas se ale v aplikacích vyskytnou grafy orientované ,například chcete-li zakódovat, kdo komu dluží peníze. Hrany jsou pak uspořádané dvojice čísel a matice A bude nesymetrická (to, že vrchol i dluží peníze vrcholu j, neznamená – a v praxi je to téměř vyloučeno – že j dluží peníze i).
Počet sousedů, které daný vrchol i má (což je de facto počet nenulových prvků na i-tém řádku matice A), je další důležitou veličinou, které se říká stupeň vrcholu) i a tradičně se značí anglickou zkratkou deg(i). Pro graf na obrázku výše je deg(1) = 2, deg(2) = 3, deg(3) = 3 a deg(4) = 2.
Teď, když jsme si načrtnuli základní pojmy, podívejme se podrobněji na to, jak se vlastně uvnitř grafů něco šíří (ať už je to informace, peníze, sádlo nebo cokoliv jiného). Budeme tedy studovat dynamiku rozložení dané kvantity mezi vrcholy grafu.
Abychom mohli pracovat s reálnými čísly, představíme si něco jednoduchého, co se dá snadno dělit, třeba kilo cukru. Asi nejjednodušší mechanismus šíření je, že každý vrchol rozdělí všechen svůj cukr rovným dílem mezi sousedy. Na dalším obrázku je tento mechanismus ilustrován pro časové okamžiky označené a, b, c. Množství cukru je uvedeno zeleně.
Kromě pravidla pro šíření cukru je nutno zadat také počáteční rozložení. Pro jednoduchost jsem zde všechen cukr přidělil vrcholu 1, ten ho pak v další iteraci rozdal všem svým sousedům (půlku dostal vrchol 2 a půlku vrchol 3) a ti ho pak v dalším časovém kroku rozdělili stejným způsobem dále. K vrcholu 1 se tak dostala šestinka kila od každého z vrcholů 2 a 3, takže vrchol 1 vlastní v této iteraci dvě šestinky, tj. 1/3 (pro zbylé vrcholy si ta zelená čísla lehce dopočítáte).
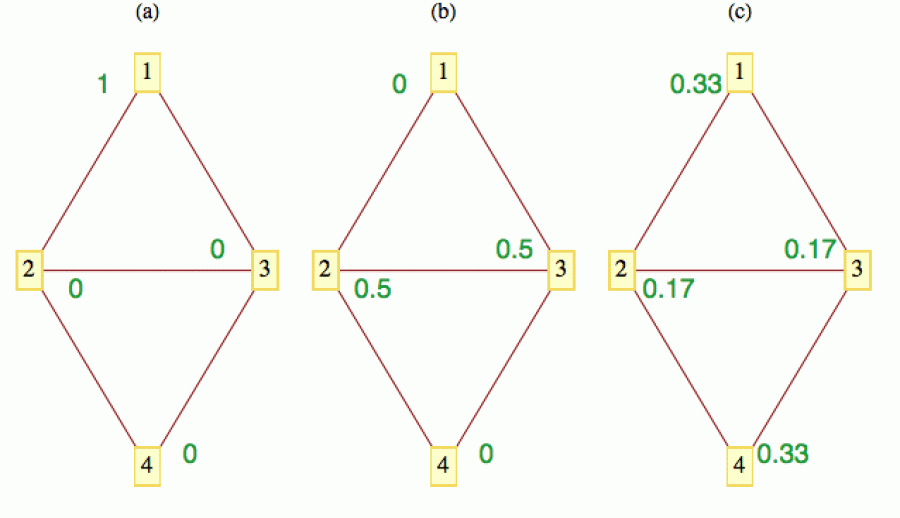
Tímto způsobem si můžeme „tok cukru“ grafem lehce spočítat na prstech a žádnou vyšší matematiku k tomu nepotřebujeme. Je to ale postup zdlouhavý a nepohodlný. Po několika krocích by nás pravděpodobně věčné počítání, kdo má komu kolik poslat, omrzelo.
Protože ta cukrová dynamika je lineární (pokud máte dvakrát více cukru, tak každý váš soused dostane dvojnásobný příděl), pokusíme se tento proces namodelovat pomocí násobení matic. Pro graf s n vrcholy si označíme rozdělení cukru mezi vrcholy v čase t pomocí vektoru:
c(t) = (c1, c2, c3, ... , cn)
kde reálné číslo ci nám říká, kolik má i-tý vrchol cukru (v čase
t).
Když si tu výše simulovanou dynamiku „toku grafem“ rozepíšeme pomocí těchto cukrových vektorů (což jsou ta zelená čísla), dostaneme pro první dva kroky:
(0,0,1,0) --> (0,1/2,1/2,0) --> (1/3,1/6,1/6,1/3) --> ...
čili symbolicky c(0) --> c(1) --> c(2)
zde c(i) není i-tá složka, ale celý cukrový vektor c v čase i
Kruciální otázka je, zda by se nám nepodařilo najít nějakou matici M (typu nxn) tak, aby se tato posloupnost v čase se vyvíjejících cukrových koncentrací dala popsat vynásobením této matice a stávajícího cukrového vektoru c. Taková matice bude popisovat přechod od jednoho rozložení v čase t k následujícímu v čase t + 1.
(*) c(t + 1) = M.c(t)
Představme si, jak toto násobení funguje. Vlevo bude i-tá složka vektoru c(t + 1) reprezentovat nové množství cukru, který bude mít i-tý vrchol v čase t + 1. Napravo bude i-tá složka skalárním součinem i-tého řádku matice M a „starého“ cukrového vektoru c(t). Toto množství by mělo reflektovat součet příspěvků od všech vrcholů se kterými je vrchol i spojen.
Přirozeným kandidátem pro M je matice sousedství A, jejíž i-tý řádek (a sloupek) v sobě nese informaci o tom, kdo je a kdo není sousedem vrcholu i. Na i-tém řádku mají vrcholy, které nejsou spojeny s i, nulu, takže od nich podle očekávání i-tý vrchol nic nedostane. Cukrové příspěvky dostane pouze od vrcholů j, které mají na i-tém řádku jedničky (tedy od jéček, které jsou s íčkem spojeny). Jen musíme mít na paměti, že tito sousedé nepředají íčkovi všechen svůj cukr, ale pouze proporcionální podíl (podle toho, kolik mají sami sousedů). Musíme tedy všechny ty jedničky vydělit počtem sousedů každého jéčka.
Tenhle závěrečný oříšek poměrně lehce vyřešíme tím, že v matici A vydělíme j-tý sloupec stupněm j-tého vrcholu, tedy číslem deg(j), které nám udává, kolik má jéčko sousedů (tj. každý sloupec matice A vydělíme počtem jedniček v tom sloupci).
Kouzelná matice M bude mít tedy následující tvar:
M(i,j) = 1/deg(j), pokud je (i,j)∈H
(a M(i,j) = 0 v ostatních případech)
Pro nahoře uvedený příklad bude mít matice M (4x4) tvar:
(0,1/3,1/3,0)
(1/2,0,1/3,1/2)
(1/2,1/3,0,1/2)
(0,1/3,1/3,0)
Všimněte si, že díky vydělení mají všechny sloupky součet 1 (pozor, to je něco jiného než jednotková délka, kde nás zajímá odmocnina ze součtu čtverců). Takovým maticím se obecně říká stochastické nebo též přechodové, protože ukazují, jak systém přechází z jednoho stavu do druhého (v našem případě jak přejít od jednoho rozložení cukru k druhému).
Můžete si sami ověřit, že
M.(1,0,0,0) = (0,0.5,0.5,0)
a v dalším kroku
M.(0,0.5,0.5,0) = (0.333,0.166,0.166,0.333)
Tímto se nám podařilo cukrovou dynamiku kompletně převést na maticové násobení. Nebudeme tedy při přechodu z času t k času t + 1 muset koumat, kdo má kolik cukru a kdo má kolik sousedů, ale prostě ten cukrový vektor v čase t pronásobíme maticí M a dostaneme okamžitě rozložení cukru v čase t + 1. A nepotřebujeme k tomu žádné účetní knihy.
Schematicky se to vydělení stupněm dá provést tak, že si zadefinujeme tzv. matici stupňů D (která má na diagonále stupně jednotlivých vrcholů a jinde nuly) a matici A pak vynásobíme zprava maticí D-1 (která bude mít na diagonále reciproké hodnoty těchto stupňů, tedy 1/deg(j)). Matici M tedy definujeme jednoduchým vztahem:
M = A.D-1
Pro náš minigraf bude D = ((2,0,0,0),(0,3,0,0),(0,0,3,0),(0,0,0,2))
Matici M se říká Markovova matice a velmi úzce souvisí s maticí popisující náhodné procházky. Má ale jednu malou vadu na kráse, na rozdíl od matice A není symetrická. Proto se v praxi používají různé symetrizace této matice, kterým se obecně říká Laplaciány grafu.
Předminule jsme viděli, že podobné matice mají stejné spektrum (kolekci vlastních čísel) a úzce související vlastní vektory. Ta symetrizace se tudíž nejlépe provede tak, že najdeme symetrickou matici, která je matici M podobná (obvykle M pronásobíme zprava maticí, která bude mít na diagonále odmocniny ze stupňů všech vrcholů, a zleva její inverzí). Výsledkem bude Laplacián L, tedy symetrická matice, podobná té Markovově.
Přestože Laplacián L má některé výpočetní výhody (jeho vlastní vektory jsou např. ortogonální), pro začátečníky je stravitelnější Markovova matice M, protože velmi názorně popisuje tu cukrovou dynamiku. Proto si ve zbytku dnešního Matykání vystačíme s ní. Zájemci o spektrální analýzu grafů by se ale s Laplaciány měli seznámit, nejlépe na podnikovém večírku ve stavu mírně podroušeném (což znamená, že si pod ochrannou rouškou notně přihýbáte).
2. Co s vlastními čísly?
Dynamika popsaná rovnicí (*) je závislá na chování vyšších mocnin matice M. Rozložení cukru v čase t bude totiž rovno:
c(t) = Mt.c(0), kde c(0) je počáteční rozložení.
V předminulém Matykání jsme viděli, že vyšší mocniny matic se nejlépe počítají z jejich rozkladu do vlastních vektorů. Proto nás nepřekvapí, že základní vlastnosti cukrové dynamiky se dají odvodit z vlastních čísel matice M (a jemnější aspekty pak z jejích vlastních vektorů). Podívejme se na ně.
Jedno vlastní číslo (a příslušný vlastní vektor) se dá uhodnout. Vezmeme si náš testovací graf a představíme si, že jako počáteční rozložení cukru c(0) dáme každému vrcholu množství odpovídající jeho stupni (zelená čísla na obrázku vpravo). Tady se to další rozdělení c(1) dá spočítat z ruky. Když každý rozdělí svůj podíl cukru rovnoměrně mezi sousedy, v čase t = 1 dostaneme přesně to samé rozdělení. Každý totiž na svého souseda přesune jeden dílek cukru (protože v počátečním rozdělení měl každý přesně tolik dílků co sousedů). Ale současně každý dostane jeden dílek od všech sousedů, takže po provedení cukrové transakce jsou všichni „na svém“.
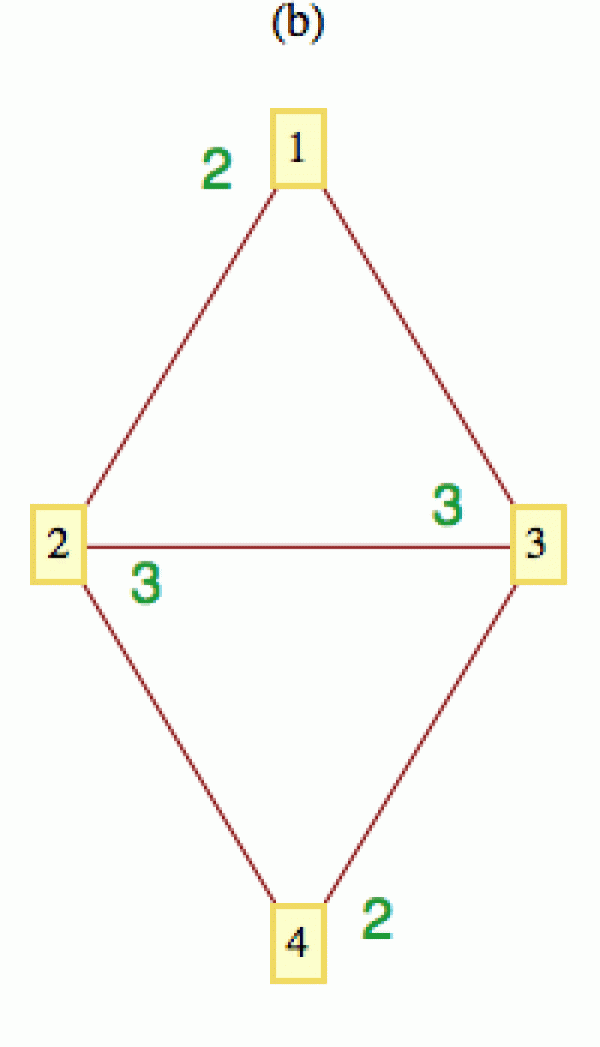
Zapsáno maticově je to prakticky definice vlastního čísla:
M.c(0) = 1*c(0)
Aniž bychom tedy s maticí M cokoliv provedli, zjistili jsme, že má jedno vlastní číslo 1. Jemu odpovídající vlastní vektor c(0) je pak tvořen vektorem stupňů. Tedy
c(0) = (deg(1), deg(2), ... deg(n))
(ten vektor c(0) můžete samozřejmě libovolně normalizovat tak, aby celkové množství cukru v oběhu bylo, řekněme, jedno kilo – ale není to nutné – předminule jsme viděli, že vlastní vektory se dají libovolně přeškálovat, aniž by ztratily své „kouzelné“ vlastnosti)
Tomuto vlastnímu číslu 1 (a jeho vlastnímu vektoru c(0)) se říká triviální, protože je má každý graf a není nutno je počítat. S ostatními už budeme mít trochu práce.
Trocha teorie: matice typu nxn má obecně n vlastních čísel (a tedy také n vlastních vektorů). Díky tomu, že M je podobná symetrické matici, její vlastní čísla budou reálná (podrobnosti zde) a všechny vlastní vektory budou existovat. Pro symetrickou matici - jako např. Laplacián L - budou ty vektory dokonce ortogonální (podrobnosti zde). Pro nesymetrickou, jako je například naše Markovova matice M, musíme ty laplaceovské pronásobit příslušnou přechodovou maticí mezi L a M, takže ortogonalitu ztratí, ale jejich existence zůstane nenarušena.
Z toho, že naše matice M je stochastická, tj. její sloupce mají jednotkový součet, navíc vyždímáme informaci, že všechna vlastní čísla leží v uzavřeném intervalu [-1,1], tj. jejich absolutní hodnota je maximálně jedna (podrobnosti zde). Pokud budete pracovat s Laplaciány, musíte dávat pozor, jak jsou přesně definované, protože každý technický detail jejich konstrukce ovlivňuje jak celkovou polohu spektra, tak hodnotu triviálního vlastního čísla. Kdo by se v tom chtěl šťourat hlouběji, může se mrknout na Geršgorinovu větu nebo na Perron-Frobeniovu větu.
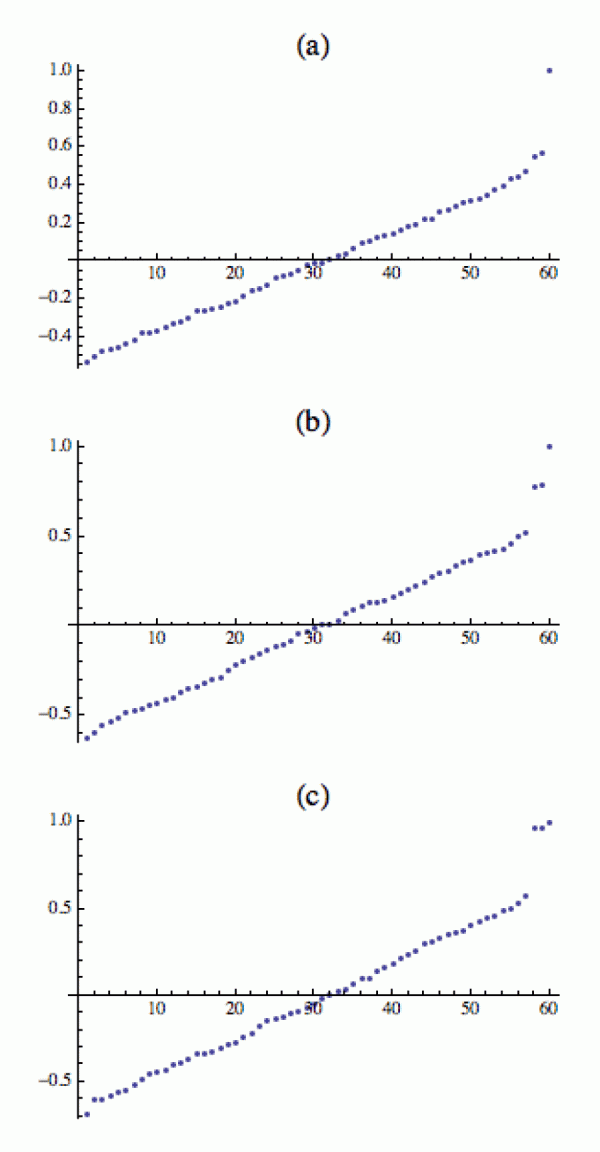
My si ale vezmeme příklad z Jáchyma a celou matici prostě hodíme do stroje. A stroj za nás všechna zbývající vlastní čísla (a jejich vlastní vektory) spočítá. Abychom se v tom trochu zorientovali, podívejme se na spektra tří grafů z úvodní sekce, tedy na vlastní čísla jejich matic M (zde seřazená podle velikosti).
Vidíte, že všechny mají vpravo triviální vlastní číslo 1 a nalevo od něho pak n-1 zbylých vlastních čísel různě rozložených v intervalu -1,1 podle vlastností příslušné matice M (a tedy příslušného grafu G). Můžete si zkusit odpozorovat nějakou pracovní hypotézu, jak všechna ta čísla (zejm. na pravém okraji) souvisí se strukturou grafu.
My se ale nejprve podíváme, jak to spektrum souvisí s cukrovou dynamikou. Každé počáteční rozložení c si rozepíšeme jako lineární kombinaci vlastních vektorů ui:
c = a1 u1 + a2 u2 + ... +
an un
(kde vektory jsou seřazené sestupně podle vlastních čísel, tj. ten první
je triviální)
Když n-dimenzionální vektor c pronásobíme maticí M (abychom dostali rozdělení cukru v dalším okamžiku), v každém sčítanci nám z definice vyskočí příslušné vlastní číslo λ:
(**) M.c = λ1 a1 u1 + λ2 a2 u2 + ... + λn an un
a když tento proces opakujeme (tedy přecházíme k vyšším a vyšším mocninám M, reprezentujícím další časové okamžiky), napravo nám vyskakují vyšší a vyšší mocniny vlastních čísel (to si dobře rozmyslete). Vše ostatní (tedy áčka a účka) zůstává stejné.
A teď už nám jen stačí si ze školy vzpomenout, jak se chovají geometrické posloupnosti. Když umocňujeme jedničku, neděje se pochopitelně nic. Jednička na miliontou je pořád jenom jednička. Ten první člen se tedy nemění. Všechny ostatní, kde vlastní čísla splňují IλnI < 1, budou konvergovat k nule. Výsledně tedy z naší rovnice vymizí a cukrová dynamika dospěje k ekvilibriu, které je násobkem prvního (triviálního) vektoru, a tedy násobkem stupňů grafu. Zajímavé je, že se k tomuto ekvilibriu propracujete zcela nezávisle na tom, komu jste na počátku svěřili kolik cukru. I když třeba dáte všechen cukr svému oblíbenci v grafu, vrcholu 99, asymptoticky to VŽDY dopadne tak, že každý má nakonec množství cukru přesně úměrné počtu sousedů, tedy přesně podle počtu svých konexí (jaké jsou sociálně politické implikace tohoto faktu si můžete rozmyslet sami).
Ty zbylé členy v rovnici (**) představují jakési oscilační módy. Důležité je, že nevymizí stejně rychle (!). Schválně chvíli umocňujte čísla 0,1 a 0,9. Uvidíte, že zatímco v prvním případě jste u nuly cobydup, v tom druhém se k nule budete blížit velmi pomalu a neochotně.
A podobně funguje naše cukrová dynamika. Vlastní čísla, která jsou (v absolutní hodnotě) blízko nule, vyšumí z rovnice (**) téměř okamžitě. Naopak ta, která jsou blízko jedničce (tedy triviálnímu vlastnímu číslu), odpovídají komponentám, jejichž vliv na dynamiku mizí velmi pomalu. Tyto komponenty v podstatě odpovídají hranicím mezi jednotlivými bublinami, které tok cukru – či jiné substance – grafem zpomalují (to uvidíme v další sekci).
To, že vlastní čísla blízká jedničce indikují počet „bublin“ v našem grafu, se dá nahlédnout ze spojitosti. Pokud má graf na začátku, řekněme, tři zcela oddělené bubliny, jeho spektrum bude mít tři triviální vlastní čísla (tedy tři jedničky), protože konstrukce, kterou jsme provedli na začátku této sekce, se dá provést v každé bublině zvlášť. Když nyní do grafu přidáme několik málo hran a bubliny trochu propojíme, celková struktura matice M se příliš nezmění, a tudíž se (ze spojitosti) příliš nezmění ani její spektrum. Jedna z těch tří jedniček zůstane zachována a ty dvě další se nepatrně zmenší a vytvoří dvě skoro jedničkové hodnoty, které vidíme na předchozím trojobrázku vpravo dole.
Na tom samém obrázku si ještě všimněte panelu (b), který ukazuje, že rovnoměrným přidáváním hran ke grafu (c) se dvě netriviální vlastní čísla budou od jedničky vzdalovat, a to také zhruba rovnoměrně. Pokud budeme hrany stále přidávat, bubliny nakonec splynou v graf (a) a ta dvě vlastní čísla se obě propadnou až na hodnotu, kde budou prakticky nerozlišitelná od náhodného šumu (ta předchozí vlastní čísla v podstatě reprezentují krátkodobé oscilační módy dané náhodným výběrem hran).
Podívejme se pro zajímavost, co se stane, pokud hrany budeme přidávat jen na rozhraní dvou bublin v pravé části každého grafu. Pak ty dvě bubliny splynou a de facto vznikne graf, který bude mít místo tří pouze dvě bubliny.
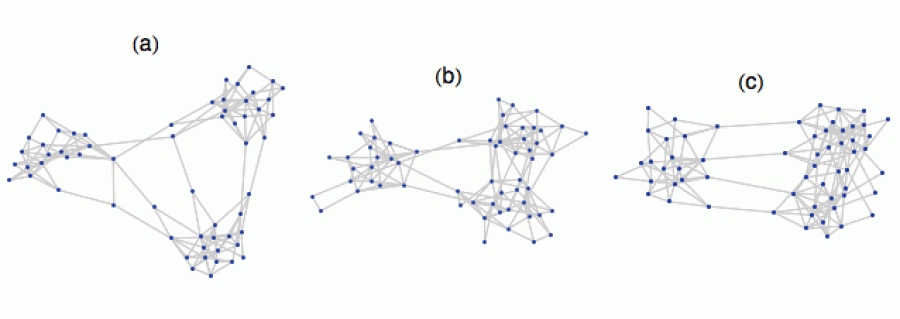
Na dalším obrázku vpravo jsou spektra těch samých tří grafů.
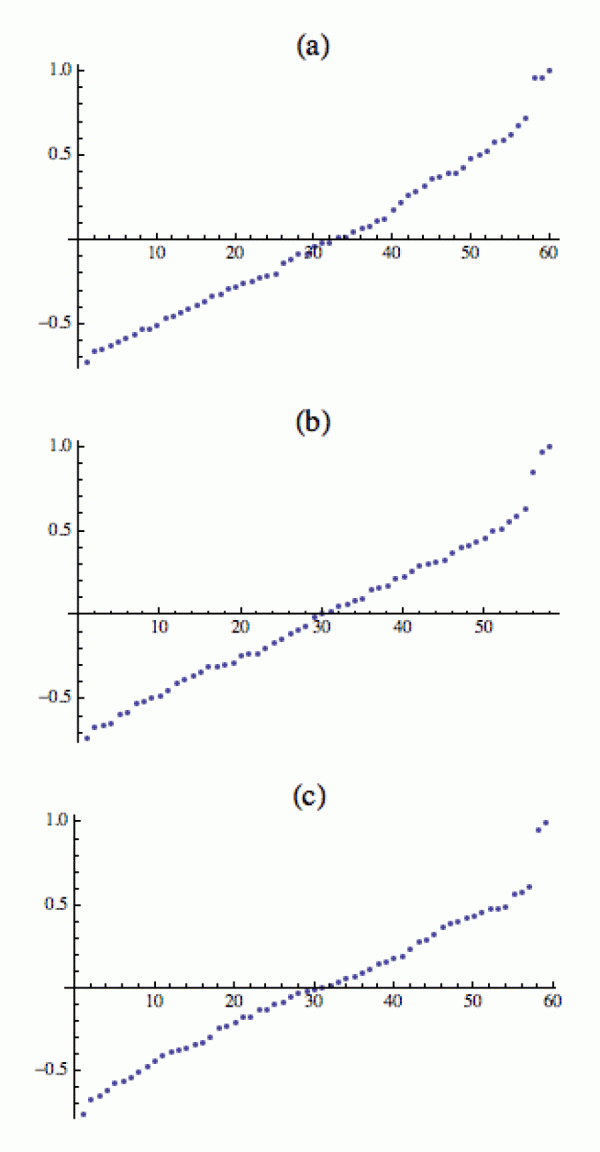
Vlastní čísla matice M tento proces krásně obnažují. Jak přidáváme hrany mezi obě pravé bubliny, jedna skoro jednička pomalu cestuje dolů a výsledně splyne se zbytkem spektra. To je přesně ten okamžik, kdy se ty pravé bubliny už prakticky nedají rozlišit, protože je mezi nimi příliš mnoho komunikátorů.
Ta druhá skoro jednička ale (na rozdíl od předchozího příkladu) zůstává poblíž jedničky, protože bublina vlevo je stále osamocena – pravé bubliny vlastně vytvořily jakousi koalici. A příkop mezi koalicí a levou bublinou se nezměnil (na předchozím trojobrázku jsem rovnoměrně zasypal všechny příkopy, a proto ve spektru sestoupily obě skoro jedničky).
Pochopitelně, pokud vystartujeme, řekněme, s pěti bublinami, tak to spektrum bude mít prostě pět vlastních čísel poblíž 1. Jednak jedničku samotnou a pak čtyři další, jejichž blízkost k jedničce bude záviset na tom, do jaké míry jsou bubliny izolované – tedy kolik mají interakcí/komunikátorů se „zbytkem světa“.
Sečteno a podtrženo: každé vlastní číslo odpovídá určitému módu „cukrové dynamiky“ (s tím, že role jednotlivých vrcholů při těchto oscilacích je určena příslušným vlastním vrcholem). Čím je vlastní číslo blíže jedničce, tím pomaleji daný oscilační mód „vyšumí“. A každá sociální bublina v grafu jedno takové vlastní číslo generuje.
Tohoto poznatku lze využít v praktických aplikacích. Většina shlukovacích algoritmů (které v grafu hledají uzavřené sociální bubliny) po vás vyžaduje odhadovaný počet komunit (což je pro grafy s mnoha tisíci vrcholů poměrně obtížné). Pohled na spektrum vám pomůže odhadnout, kolik z vašich komunit je uzavřených (vlastní čísla hodně blízko k jedničce) či částečně uzavřených (vlastní čísla jakž takž blízko k jedničce). I to je však pro velké grafy do jisté míry subjektivní odhad, protože musíte rozhodnout, co to ta blízkost jedničce vlastně znamená (tedy kolik komunikátorů mezi bublinami jste ochotni připustit). Jako poměrně dobrá heuristika pak funguje největší díra v horní části spektra. Tedy místo, kde se vlastní čísla najednou propadnou.
A jak tedy změřit rozdělenou společnost? Ze spektra se dá odvodit několik zajímavých indikátorů. Jedním z nich je v každém čase t spočítat průměr několika prvních netriviálních vlastních čísel a čím je tento průměr blíž k jedničce, tím je společnost rozdělenější. Jiný přístup spočívá ve spočítání spektra pro náhodný graf se stejným počtem vrcholů a hran a kumulativní rozdíl mezi oběma spektry pak také kvantifikuje rozdělenost společnosti. Pokud je graf společnosti kompaktní, příslušný náhodný graf bude mít velmi podobné spektrum.
Mimochodem, kdo dobře studoval geometrické řady, tak si možná vzpomene, že konvergence k nule se může dít v zásadě dvěma způsoby. Pokud umocňujete, řekněme, 0.5 na vyšší a vyšší mocniny, výsledek se monotónně zmenšuje, až vymizí úplně. Pro záporné koeficienty, řekněme -0.5, do nuly doskáčete tak, že budete alternovat mezi pozitivními a negativními čísly (jejichž absolutní hodnota se bude zmenšovat k nule).
Pro cukrovou dynamiku to funguje podobně. Jsou-li vlastní čísla záporná (ale v absolutní hodnotě pod jedničkou), příslušné členy v rovnici (**) se budou zmenšovat, ale alternujícím způsobem (tj. neustálým prohazováním znaménka). Protože stopa matice M (součet prvků na diagonále) je nula, součet všech vlastních čísel musí být taky nula (podrobnosti zde). To znamená, že alternujících módů musí být poměrně dost (musí nejen vyrušit všechny nealternující módy, ale ještě vykompenzovat tu triviální jedničku). Pro zajímavost dodám, že pokud jsou alternující módy extrémní (tj. vlastní čísla jsou blízká -1), v grafu se začnou objevovat komponenty, které mají bipartitní charakter. To je ale pro sociální grafy velmi vzácný úkaz, takže si s ním nebudeme lámat hlavu.
3. Co s vlastními vektory?
Vzhledem k tomu, že pro graf s n vrcholy dostaneme z matice M přesně n vlastních čísel, mohlo by se zdát, že každé z nich je nějakým způsobem spojeno s jedním vrcholem grafu. Tak tomu ale není. Každé vlastní číslo je odrazem vlastností celého grafu a v podstatě ukazuje, jakou rychlostí rozkladová komponenta daná příslušným vlastním vektorem ui z cukrového vektoru „odezní“.
U vlastních vektorů je tomu jinak. Každá z jeho n souřadnic skutečně odpovídá jednomu z vrcholů grafu (přesně v tom pořadí, v jakém jsou reprezentovány v matici sousedství A). Tedy první souřadnice ukazuje na „množství cukru“ v prvním vrcholu, druhá v druhém atd. Vlastní vektory matice M – stejně jako cukrové vektory – jsou s vrcholy grafu nerozlučně spojeny.
Zvídavý čtenář si při pohledu na rozkladovou rovnici (**) pomyslí, co se asi děje se vším tím cukrem, který je obsažen v těch netriviálních komponentách, konvergujících s přibývajícím časem k nule. Z mechaniky našeho procesu jasně vyplývá, že celkové množství cukru v grafu se nemění. Jak se tedy ten cukr může z rovnic vytrácet? On se taky ve skutečnosti nevytrácí. Zatímco cukrové vektory c mají nezáporné souřadnice (ukazující kolik cukru ten který vrchol má), každý z vlastních vektorů ui je pouze abstraktním vektorem z příslušného n-dimenzionálního prostoru a nemusí mít nutně kladné souřadnice. Podívejme se na to podrobněji.
Triviální vektor samozřejmě kladné (resp. nezáporné) souřadnice má – to jsme viděli v předchozí sekci. Ale netriviální vlastní vektory jsou mixované, tedy míchají kladné souřadnice se zápornými. Dokonce se dá ukázat, že pro stochastické matice (a M takovou je) jsou jejich netriviální vlastní vektory „vybalancované“, to znamená, že prostý součet všech jejich souřadnic je roven nule. Jinými slovy, ty kladné a záporné souřadnice vektoru se přesně vyruší (nápověda k důkazu je zde a zde).
O zákon zachování cukru tedy strach mít nemusíme, každý z těch netriviálních korekčních členů je přesně vybalancovaný (jeho celková „hmota“ je rovna nule). Přestože vliv těchto komponent postupně slábne, na celkové množství cukru v grafu to nemá vliv (v každém z netriviálních vlastních vektorů jsou kladné a záporné odchylky od ekvilibria přesně vyvážené). Ať je pokles daný vlastním číslem jakýkoliv, něco krát nula bude vždy nula.
Aby nás moc nerozbolela hlava, podívejme se na konkrétní příklad. Vezměme si dvoubublinový graf s 50 vrcholy: pro jednoduchost očísluji jeho pravou „frakci“ 1-25, levou 26-50. Spektrum (vpravo) má podle očekávání dvě vlastní čísla blízko jedničce: jednak tu triviální jedničku jako takovou (tu má každý graf) a pak druhou skoro jedničku, která nám prozrazuje, že tento graf vznikl mutací dvou zcela oddělených grafů.
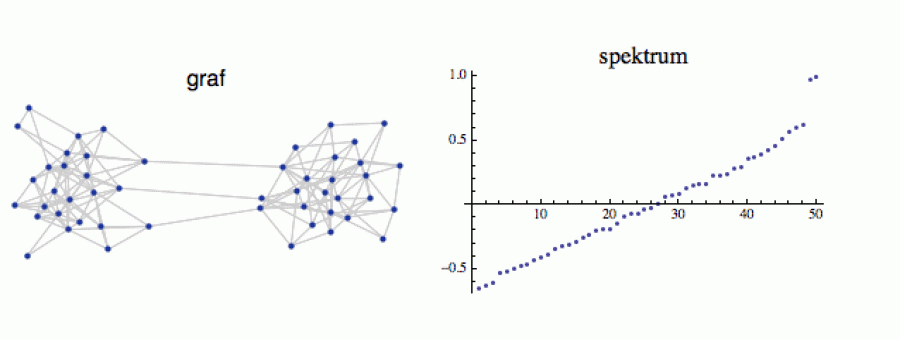
Nyní se podívejme na první tři vlastní vektory. Protože pracujeme ve vysokodimenzionálním prostoru (v tomto případě je n = 50), zobrazím je trochu netradičním způsobem. Prostě vynesu jejich 50 souřadnic za sebou, jako by to byly členy nějaké posloupnosti, a spojím je čarou.
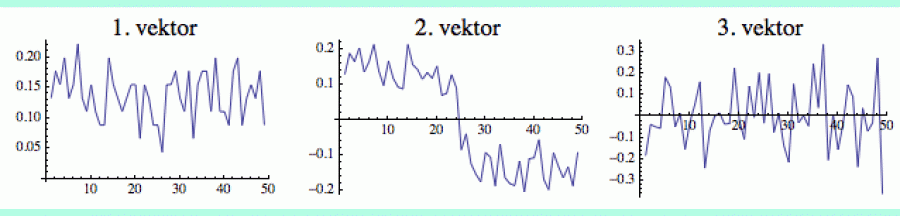
První vektor je triviální a jeho souřadnice jsou vesměs kladné: i-té číslo ukazuje (normalizovaný) počet sousedů i-tého vrcholu. Ta kladnost je věcí konvence. Klidně jsem mohl vektor vynásobit -1 a pak by všechny souřadnice byly záporné. Důležité je, že mají stejné znaménko (to je mimochodem jeden z důsledků již zmíněné Perron-Frobeniovy věty).
Prostřední obrázek ukazuje vlastní vektor příslušný prvnímu netriviálnímu vlastnímu číslu (což je v tomto případě „skoro-jednička“ λ = 0.96). Tento vektor má velmi specifickou strukturu. Jeho souřadnice z pravé bubliny (vrcholy 1-25) mají kladnou hodnotu, v levé bublině (vrcholy 26-50) jsou souřadnice záporné. Ten první netriviální vektor nám tedy přesně prozradí, kdo je v které bublině.
I tento fenomén lze pochopit ze spojitosti. Předtím, než se dvě bubliny „slily“, existovaly v oddělené formě, a graf měl tudíž dva triviální vlastní vektory (jeden pro pravou bublinu, druhý pro levou), jejichž souřadnice měly vesměs stejné znaménko. Protože ale po „slití“ musely být vlastní vektory vybalancované, nezbylo jim než vzít hodnoty z jedné bubliny s jedním znaménkem a z druhé s opačným.
Všechny ostatní netriviální vlastní vektory už vypadají podobně jako ten z pravé části obrázku. I ony jsou vybalancované, ale už neukazují žádnou další strukturu a jsou v podstatě rozloženy náhodně (protože kromě respektování dvou počátečních bublin jsem hrany v grafu G přiděloval náhodně). Vzhledem k tomu, že jejich vlastní čísla jsou poměrně malá, jejich vliv na cukrovou dynamiku v grafu poměrně rychle vymizí.
Struktura patrná na tom prostředním obrázku je základem algoritmů využívajících spektrálních vlastností grafů k jejich rozdělení na více či méně uzavřené komunity. V našem případě by stačilo do jedné komunity umístit vrcholy, v nichž má ten první netriviální vlastní vektor kladné souřadnice, a do druhé komunity ty se zápornými souřadnicemi. Díky našemu očíslování bylo rozdělení do komunit očividné, ale u grafů s mnoha tisíci vrcholy se takový algoritmus hodí.
Samozřejmě, pokud má graf tři nebo více komunit, pak musíme použít i další netriviální vektory. A protože máme jen dvě možná znaménka (plus a minus), je pak třeba výsledky kombinovat. Další trojice obrázků ukazuje první tři vlastní vektory grafu se třemi komunitami (pravá část dnešního úvodního obrázku). Ty sedí v pozicích: 1-20, 21-40 a 41-60.
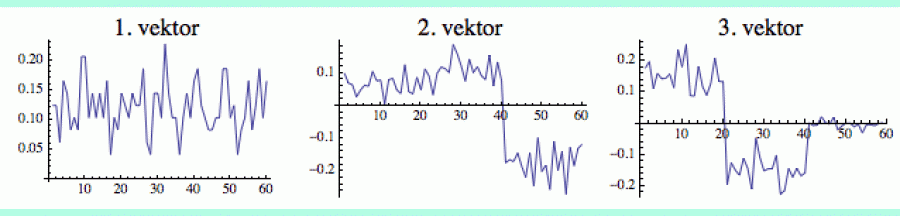
V tomto případě má i ten třetí vektor velmi viditelnou strukturu, kterou můžeme použít k nalezení všech komunit (ten druhý vektor totiž nedokázal rozlišit mezi 1. a 2. komunitou). Teprve čtvrtý vektor (a další za ním) by ukázal náhodné rozložení, jak jsme to viděli v předchozím případě.
Ale to není všechno. Vlastní vektory nám nejen ukazují, kdo patří do jaké komunity, ale i jakou roli ve své komunitě hraje. Tedy zda je zapšklým „partajníkem“, který komunikuje pouze se svými pobratimy, anebo zda patří k těm několika komunikátorům interagujícím i s lidmi v jiných komunitách.
Na dalším obrázku vlevo jsem vzal dvoubublinový graf, a protože každá souřadnice vlastního vektoru odpovídá jednomu vrcholu, obarvil jsem vrcholy podle hodnoty souřadnic prvního netriviálního vektoru. Čím kladnější, tím modřejší, a čím zápornější, tím červenější. Barva je zde indikátorem komunity. „Pravičáci“ modře, „levičáci“ červeně.
Protože si tento graf můžeme představit jako malou modifikaci dvou zcela oddělených grafů (odpovídajících oběma bublinám), který měl každý svůj vlastní triviální vektor úměrný stupňům vrcholů, i zde jsou barevné odstíny zhruba úměrné počtu sousedů každého vrcholu. Ale ne úplně přesně (jsou to jen jakési skoro stupně). Např. dva vrcholy v západní oblasti modré bubliny jsou o něco světlejší, než bychom podle jejich vysokého stupně čekali (a totéž platí pro vrcholy ve východní oblasti červené bubliny). Protože tyto vrcholy komunikují i s „protější“ stranou (která má opačné znaménko), na jejich barevném tónu se to projevilo.
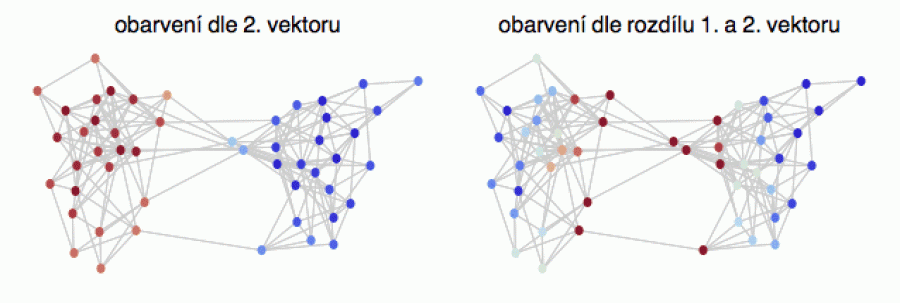
A to otevírá následující možnost. Spočítáme si, jakou barvu by měl daný vrchol mít (na základě stupně, a tedy 1. vektoru) a kterou barvu skutečně má (na základě skoro stupně a tedy 2. vektoru), a z jejich rozdílu spočítáme nové barevné ohodnocení (pravá část obrázku). Technicky zde vrcholy barvíme podle rozdílu prvního a druhého vlastního vektoru (ten druhý vezmeme v absolutní hodnotě – abychom nemuseli manipulovat se zápornými „skoro stupni“).
Vidíte, že ty „zapšklé“ vrcholy uvnitř obou komunit teď mají modré odstíny (radikální stoupenci, kteří by si s druhou stranou nikdy nezadali), zatímco vrcholy komunikující i se svými ideologickými oponenty jsou obarveny červeně (to jsou umírnění stoupenci své ideologie).
Z pohledu strukturální analýzy grafů se tedy dá říci, že každý netriviální člen v rovnici (**) odpovídá určitému rozdělení grafu na modré „klaďase“ a červené „záporáky“ podle vlastního vektoru. Tyto členy představují korekce „cukrové dynamiky“. Čím je vlastní číslo (v absolutní hodnotě) blíž k jedničce, tím pomaleji daná odchylka odezní. Architektura grafu se pak dá odečíst z těchto vlastních čísel (a jejich vektorů), neboť reprezentují odchylky s největší „trvanlivostí“.
V praxi se tento typ spektrální analýzy používá ve třech základních rovinách:
V první – v rovině vlastních čísel – slouží ke zkoumání jednolitosti, respektive roztříštěnosti grafu jako celku. V druhé – v rovině individuálních vlastních vektorů – zkoumá funkční role jednotlivých vrcholů grafu z pohledu jeho vnitřní struktury. A konečně ve třetí rovině – o té jsem se zatím nezmínil – si můžeme vzít prvních k netriviálních vektorů (kde k se obvykle volí podle toho, kolik vlastních čísel je „blízko“ jedničce) a z jejich i-tých souřadnic vytvořit reprezentaci i-tého vrcholu (a tedy celého grafu) v nějakém k-dimenzionálním prostoru. Tomuto triku se říká vnoření grafu (graph embedding) a z něho lze odvodit další užitečné vlastnosti (viz např. toto pdf). Spousta softwarových knihoven ho nabízí jako standardní vybavení.
Pro české čtenáře bych ještě rád vypíchl fakt, že lví podíl na rozvoji této disciplíny měl český matematik Miroslav Fiedler, jehož článek z roku 1973 ukázal na důležitou roli matic a jejích spektrálních vlastností v teorii grafů. Na jeho počest se tomu prvnímu netriviálnímu vektoru říká Fiedlerův vektor.
Článek je redakčně upravenou verzí blogového příspěvku na serveru iDNES.cz. Publikováno s laskavým svolením autora. Další díly a původní texty jsou dostupné na blogu Jana Řeháčka.