Dnes si posvítíme na jednu z nejfantastičtějších struktur celé elementární matematiky. Nejprve se podíváme na konstrukci racionálních čísel (zlomků) pomocí Fordových kružnic a potom na výsledný Stern-Brocotův strom.
V minulém Matykání jsme si řekli, že racionální čísla tvoří jakousi kostru našeho číselného systému, a to přesto že je jich pouze spočetně mnoho (všech desetinných čísel je nespočetně mnoho). Vlastnosti této kostry určují – stejně jako u lidského těla – strukturu celého systému, a proto je jejich poznání klíčem ke studiu reálných čísel.
Protože všechny zlomky větší než 1 (např. 5/3 nebo 21/10) vzniknou jako převrácená hodnota čísel menších než 1 (tedy 3/5 a 10/21), pro pochopení struktury racionálních čísel nám stačí, když se omezíme na zlomky mezi 0 a 1. Pro ty, které jsou větší než 1, pak objevenou strukturu prostě převrátíme vzhůru nohama a pro záporné hodnoty ji opatříme slušivým minusem.
Bohužel, ve škole se racionální čísla (zlomky) definují způsobem, který jejich vzájemné propojení spíše zahaluje, než odkrývá. Když jsem byl na základce, tak nám paní učitelka nejprve vysvětlila, že zlomky dostaneme jako podíly celých čísel, a potom nám pro lepší vizuální představu nakreslila na tabuli zhruba tento obrázek: rozdělením jednotkové úsečky na n stejných dílků dostaneme všechny n-tiny (tedy třetiny, čtvrtiny, pětiny atd.).
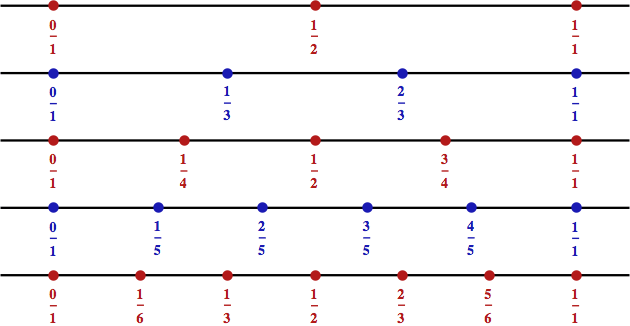
To není špatná představa (a pro přímočarou dětskou duši je možná i stravitelnější), ale má dva lehké nedostatky.
Za prvé: Co chvíli musíte zápasit s faktem, že ne všechny zlomky, které si takto nabrnkáte, jsou v základním tvaru (tj. nedají se zkrátit). Například pro šestiny je v základním tvaru pouze 1/6 a 5/6. Ostatní se zkrátit dají, takže na dané úsečce vidíme i čísla, která se objevila už v předchozích krocích (např. 2/6 = 1/3).
Za druhé: Tím, že pětiny, šestiny, sedminy atd. vyrábíme odděleně, tak není vidět žádné propojení, které by prostupovalo napříč jednotlivými patry. Zlomky si vytváří jakési uzavřené komunity (pětiny kamarádí pouze s pětinami) a jejich globální vztahy jsou zcela neprůhledné.
Oba tyto nedostatky odstraníme, pokud si vytvoříme racionální čísla pomocí Fordových kružnic. Než tak učiníme, podívejme se, jak můžeme s pomocí kružnic zkonstruovat celá čísla.
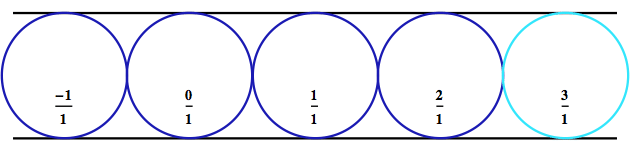
Mezi dvě přímky „nakutálíme“ kružnice a tam, kde se ty kružnice
dotýkají podlahy (osy x), si vyznačíme jejich polohu. Pokud si zvolíme
jednotky tak, že poloměr kružnic je 1/2 (a tedy průměr je 1), vyjdou nám
dotykové body přesně v celých číslech: ... -1, 0, 1, 2, 3, ... (na
obrázku jsem celá čísla zapsal už jako zlomky). Pro pochopení Fordových
kružnic je důležité si uvědomit, že každé další celé číslo (zde na
obrázku jsem si vybral číslo 3) dostaneme tak, že do „štěrbiny“ vpravo
vepíšeme kružnici, která se dotýká následujících tří kružnic:
předchozí kružnice, „podlahy“ a „stropu“ (a nezapomeňte, že na
přímku se díváme jako na kružnici s nekonečným poloměrem). Taková
kružnice existuje právě jedna – ta bleděmodrá. Je to podobné, jako když
jste na střední škole vepisovali kružnici do trojúhelníku – tam se
kružnice také musela dotýkat tří objektů. A takto si vytvoříme všechna
celá čísla. Postupně vpisujeme další a další kružnice a zapisujeme si
do notýsku, kde se dotýkají podlahy (osy x).
Koho zajímají geometrické problémy související s tečnými kružnicemi, může se podívat na Apolloniovu úlohu (anglicky Problem of Apollonius), popřípadě na Descartes' Theorem.
Fordovy kružnice
Fordovy kružnice zobecňují předchozí konstrukci a ukazují, co by se stalo, kdybychom kružnice začali vepisovat nejen na konec řady, ale i do mezilehlých prostorů na podlaze.
Protože jsme si řekli, že stačí, když pochopíme strukturu racionálních čísel mezi 0 a 1, začneme tím, že si z předchozího obrázku vypůjčíme dva modré kruhy odpovídající 0 a 1, pomalu začneme vpisovat kružnice mezi ně a budeme zkoumat, kde se dotýkají osy x (tedy podlahy).
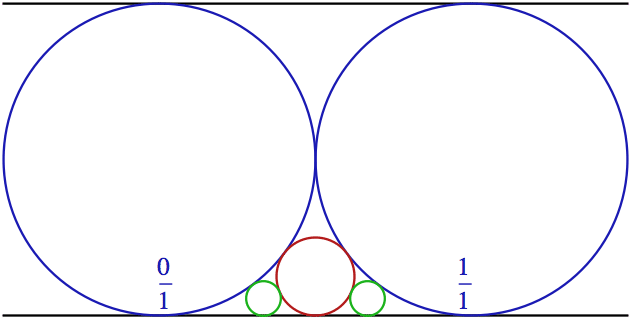
První červená kružnice je jednoduchá. Celý obrázek je symetrický,
protože dvě modré kružnice mají stejnou velikost, takže dotek s osou x (podlahou) musí být přesně mezi 0 a 1 – tedy v bodě 1/2. A máme první
opravdové racionální číslo!
Dál už to tak jednoduché není. Zelené kružnice neleží mezi stejně velkými kružnicemi, takže symetrie nám zde nepomůže. Pokud hádáte na 1/4, tak prohádáte zimník. Je potřeba si udělat výpočet. Kdo se na něj chce podívat, může si v závěru článku přečíst přílohu Jauvajs. Tady vám jenom prozradím, že zelené kružnice se dotýkají podlahy v bodech 1/3 a 2/3. A máme další dvě racionální čísla. A současně další dvě Fordovy kružnice.
Co je na této konstrukci vlastně fantastického? Ze střední školy si možná pamatujete, že z pohledu analytické geometrie je kružnice popsána kvadratickou rovnicí. Při hledání bodů dotyku tedy v podstatě řešíme soustavy kvadratických rovnic. A to znamená, že nám jako řešení mohou vzniknout odmocniny – tedy čísla iracionální – a to i v případě, že parametry kvadratických rovnic jsou celá čísla (viz sekce Jauvajs). Přesto v této konstrukci při hledání dotykových bodů dostáváme pouze zlomky a to je takový malý zázrak. Velký zázrak je pak to, že takto dostaneme úplně všechny zlomky (to ale uvidíme až příště).
Na dalším obrázku vám ukážu, jak hledání Fordových kružnic pokračuje. V prvním sledu do 4 štěrbin z předchozího obrázku vepíšeme 4 fialové kružnice. Tím dostaneme 8 štěrbin a do nich vepíšeme 8 žlutých kružnic. Barevně jsem vyznačil také dotykové body – tedy racionální čísla, která kružnice de facto reprezentují.
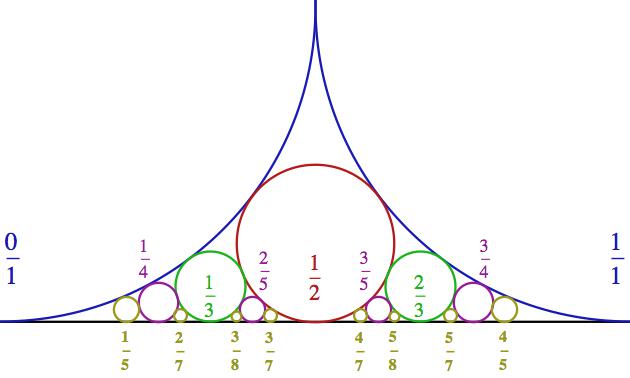
(větší verze Fordových kruhů je zde)
Za zmínku stojí, že každá zelená kružnice vyprodukuje dvě fialové kružnice po straně. A obdobně každá fialová kružnice dá vzniknout dvěma žlutým. Toto pozorování se nám bude hodit při konstrukci Stern-Brocotova stromu. Na obrázku je teď 16 štěrbin, a pokud bychom chtěli, mohli bychom v produkci zlomků pokračovat tak, že bychom do nich vepsali 16 malilinkatých kružnic. A potom 32, 64 a tak dále, až bychom si nasekali všechna racionální čísla mezi 0 a 1.
Všimněte si, že každá kružnice se kromě podlahy dotýká přesně dvou kružnic nad sebou. To nám umožňuje definovat dva „rodiče“ pro každou kružnici a potažmo pro každý zlomek. Na dalším obrázku si to ukážeme ve výřezu.
Mezi podlahu a kružnice odpovídající zlomkům 4/7 a 3/5 jsme vepsali oranžovou kružnici a výpočtem (viz sekce Jauvajs) jsme zjistili, že se tato dotýká podlahy v bodě 7/12. Takže rodiče zlomku 7/12 jsou 3/5 a 4/7. Koho při tom určíme jako „tátu“ a koho jako „mámu“, je věcí konvence. Protože táta je v životě obvykle větší, vyberu pro něj kružnici s větším poloměrem. A protože (jak uvidíme níže) poloměr kružnice odpovídající zlomku a/b je 1/2b2, tak za tátu považuji vždy číslo s menším jmenovatelem.
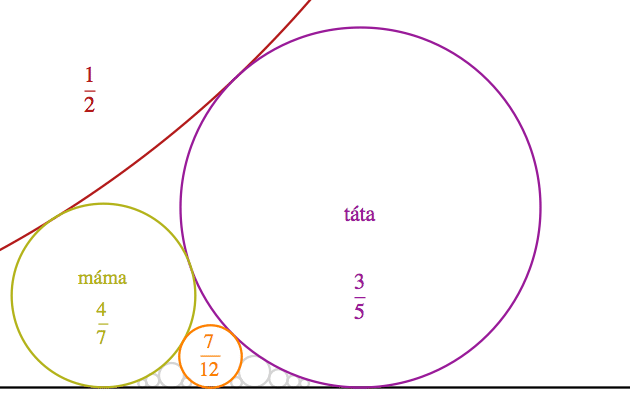
Možná jste si všimli, že oranžový zlomek vznikne tak, že zlomky
rodičovské prostě „blbě sečteme“ – jako to dělají někteří
lajdáci na základní škole – tedy sečteme čitatele a jmenovatele
zvlášť. Zlomky se takhle samozřejmě nesčítají, ale dotykový bod nově
zplozené kružnice se přesně takhle spočítat dá (technické podrobnosti v závěru článku). Díky této vlastnosti také nikdy nedostaneme zlomek,
který by nebyl v základním tvaru (tj. který by se dal zkrátit).
Mimochodem, v angličtině se tečným kružnicím říká kissing circles (líbající se kružnice), takže vidíme, že na zplození potomka se kružnice nadřou podstatně méně než lidé – stačí se políbit. I s pojmenováním potomka jsou potom menší potíže. Prostě tatínka a maminku „blbě sečteme“ a je hotovo. Za domácí úkol si můžete spočítat, jaké zlomky odpovídají světle šedým kružnicím (ta šedá nejvíc nalevo odpovídá zlomku 19/33).
Vepsané kružnice jsou samozřejmě menší a menší a po chvíli nejsou vidět ani na tomto výřezu, takže by se hodil nějaký schematický diagram, kam bychom si mohli zapisovat racionální čísla tak, jak nám je Fordovy kružnice vyplivují. Takový diagram existuje a říká se mu Stern-Brocotův strom (zde je míněn strom binární, nikoliv kaštan).
Stern-Brocotův strom
Stern-Brocotův strom se snaží výše popsanou strukturu zachytit ve formě přehledného diagramu. To se většinou dělá tak, že zaznamenáme pouze pojítko mezi zlomkem a jeho maminkou – koneckonců pupeční šňůra nás poutá také pouze k maminkám. Tatínky si z diagramu musíte odvodit sami (a to tak, že si „nad daným zlomkem“ najdete nejbližší zlomek na druhé straně – tedy je-li maminka nalevo, najdete tatínka napravo a naopak).
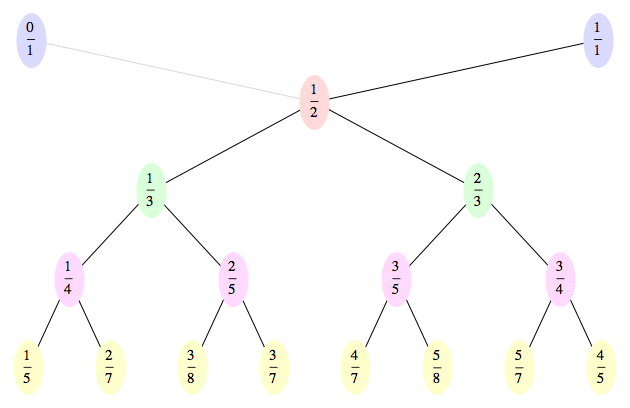
Nejprve se podívejme na zjednodušenou verzi tohoto stromu, která odpovídá druhému obrázku předchozí sekce. Je s ním i barevně sladěna (tedy modrým kružnicím odpovídají modrá pole atd.)
Na následujícím obrázku přidáme další dvě úrovně. Tentokrát jsem je
všechny obarvil žlutě, pouze dva zlomky jsem cvičně označil zeleně,
abyste si mohli natrénovat své schopnosti při určování rodičů. Pro tyto
dva zlomky jsem obarvil maminky červeně a tatínky modře. Pokud si chcete
hledání rodičů dále procvičit, najděte si v levé části spodní řady
číslo 4/15. Jeho maminku a tatínka si vyhledejte v diagramu a ověřte si,
že když maminku s tatínkem „blbě sečtete", dostanete skutečně 4/15.
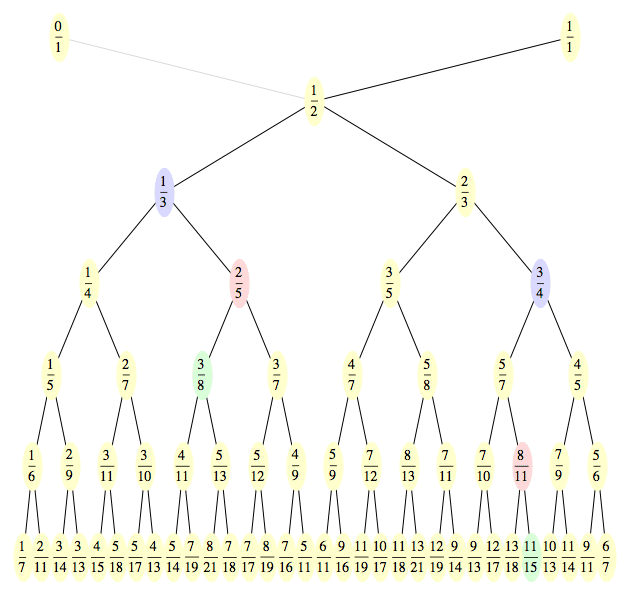(větší verze Stern Brocotova stromu je zde)
Tady vidíte vztahy mezi zlomky jako na dlani. Zlomek 3/7 je tatínkem zlomku
7/16 a zlomek 5/8 je babičkou (z matčiny strany) zlomku 9/14. Ze školního
diagramu by to tak lehce odvodit nešlo.
A závěrem ještě malá zajímavost: v jednom z článků fraktální série jsem popsal roli samopodobnosti při vzniku těchto fascinujících geometrických obrazců. Vzhledem k tomu, že fraktály jsou v této sérii generovány pomocí prosté kvadratické rovnice, nabízí se otázka, kde se v rovnicích ta samopodobnost bere. A tady vidíme odpověď: samopodobnost není v rovnicích, ale je zabudována přímo v našem číselném systému.
Každý úplný binární strom je totiž samopodobný, to znamená, že jeho části jsou podobné celku. Když se postavíte do dvou libovolných uzlů – třeba do těch, co jsou na předchozím obrázku označeny modře – a podíváte se pod sebe, tak vidíte v podstatě identickou strukturu: dva uzly přímo pod sebou a z každého vybíhají další dva uzly, a z nich zase dva poduzly a tak dále až do nekonečna. Konkrétní čísla, která pod sebou vidíte, jsou pro dva modré uzly samozřejmě jiná, ale základní struktura grafu je stejná.
S těmi různými čísly se to však dá zaonačit ještě následujícím fíglem. Představte si, že jste v Londýně a vidíte budovu, která se nápadně podobá květinářství, pouze je na ní napsáno „Flower Shop“. Kdyby se jmenovala „Květinářství“, tak koukáte na přesnou kopii toho, co máte doma na rohu. Tomu se dá pomoci tím, že si výraz „flower shop“ naťukáte do překladače, a ejhle! Dostanete skutečně „květinářství“. Takže dvě prodejny jsou si nejen podobné, ale po příslušném překladu jsou takřka identické. Ale museli jsme trochu ťuknout.
Se stromem to funguje obdobně, jen si musíme najít vhodný překladač. Existuje zázračná formulka, která vám všechny zlomky pod prvním modrým bodem (1/3) převede na ty druhé (pod 3/4) a není ani moc komplikovaná – je to podíl dvou lineárních polynomů.
(-3x + 2) / (-5x + 3)
Když do ní za x dosadíte 1/3, dostanete 3/4. Modrý bod se převedl na modrý bod. A teď se podíváme pod ně. Dosadíme-li 1/4, dostaneme 5/7, a když dosadíme 2/5, vyjdou nám 4/5. Zatím dobrý, všechno šlape. Uzly, které mají stejnou pozici vzhledem k oběma modrým bodům, se skutečně převádí na sebe. A teď se podíváme o úroveň níž. Udělejte z prvního modrého bodu cik-cak a dostanete se do 3/8. Ty si dosadíme do formulky a vyjde nám 7/9. A to je přesně stejné cik-cak z druhého bodu! Pokud si stále myslíte, že je to podvod, zkuste další úroveň. Do formulky dosadíme třeba 4/9 a vyjde nám 6/7. Přesně bod, který očekáváme! Jinými slovy, vzoreček nám přesně převede všechny zlomky pod prvním modrým bodem na odpovídající zlomky pod tím druhým.
Kouzlo? Bezesporu. Matematika je plná kouzel.
Wikipedia: Ford
Circles
Wikipedia:
Stern-Brocot Tree
Příloha: Jauvajs! To bolí! Do hlavy ne!
(pouze pro otrlé)
Pro zájemce ještě pár technických detailů o tom, jak se dotykové body počítají.
Představme si, že máme dvě líbající se kružnice (viz obrázek níže) a chtěli bychom spočítat, kde leží kružnice, která tímto polibkem vznikne – tedy ta, která je vepsaná mezi ně a podlahu (ta oranžová).
Nejdříve si musíme zavést značení. První kružnice bude mít střed v bodě (a/b, 1/2b2) a ta druhá v bodě (c/d, 1/2d2). Pokud vás zajímá, odkud se vzal výraz pro druhou souřadnici, pak vězte, že u prvních (modrých) kružnic nahoře je to vidět přímo z geometrie – např. kruh pro bod 0 má střed v bodě (0/1, 1/2). U dalších to pak vyplývá z výpočtu. Celkově nám první (x-ová) souřadnice středu ukazuje, kde se kruh dotýká podlahy, a po ní tedy paseme především – jak za chvíli uvidíme, je to vždy nějaký zlomek. Druhá souřadnice – jak již bylo naznačeno – se pak dopočítá a je vždy rovna výrazu: jedna lomeno dvakrát jmenovatel toho zlomku na druhou.
A ještě jedna vlastnost je pro konstrukci důležitá. Pokud se dvě Fordovy kružnice dotýkají, tak x-ové souřadnice jejich středů, tedy a/b a c/d, splňují vztah (ad - bc)2 = 1. U prvních kružnic je to opět vidět z geometrie (jsou to kružnice reprezentující čísla 0/1 a 1/1) a pro ty další to vyplyne z výpočtu (proč je to důležité, uvidíme příště). A teď už k vlastní konstrukci.
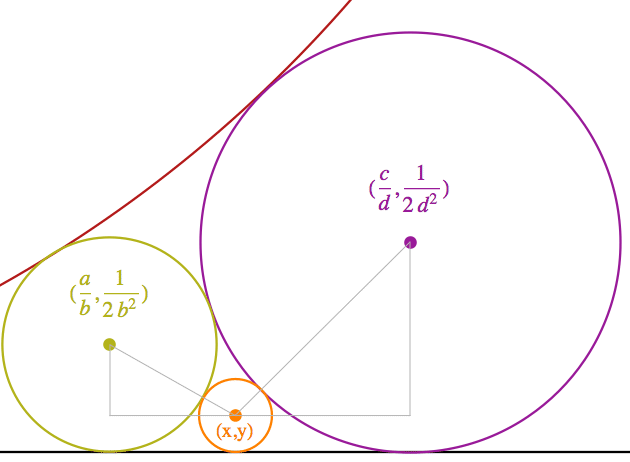
Fialová a žlutá kružnice jsou zadány (takže čísla a, b, c, d známe) a my chceme spočítat kružnici oranžovou, která se dotýká podlahy (osy x) a obou daných kružnic. To znamená, že chceme znát souřadnice jejího středu
(x,y) a poloměr r (tím bude kružnice plně určená). Na první
pohled máme tři neznámé (x, y, r), takže bychom potřebovali tři rovnice.
Naštěstí z toho, že kružnice se dotýká podlahy (osy x), vyplývá, že
její poloměr je roven souřadnici y, takže máme jen dvě neznámé
(x,y) a stačí nám tedy pro ně najít dvě rovnice. Ty vyplynou z Pythagorovy
věty pro dva pravoúhlé trojúhelníky vyznačené šedě na obrázku.
Vodorovná přepona je rozdíl x-ových souřadnic, svislá je rozdíl y-ových a přepona je součet poloměrů. Protože poloměr je ale roven y-ové
souřadnici středu, je přepona rovna součtu těchto souřadnic.
Když si tuto slovní verzi Pythagorovy věty přepíšeme do symbolů, dostaneme dvě kvadratické rovnice – jednu pro každý šedý trojúhelník. To jsou ty modré rovnice. No a zbytek je už jen algebraická manipulace. Nejprve dva členy s y roznásobíme a obě modré rovnice zjednodušíme na ty červené. Pak první červenou vynásobíme b2 a tu druhou d2. A protože obě rovnice budou mít napravo 2y, jejich levé strany se také musí rovnat a to nám dá zelenou rovnici. Tady už jsme eliminovali y, takže máme pouze jednu rovnici pro jednu neznámou (a, b, c, d jsou daná čísla).
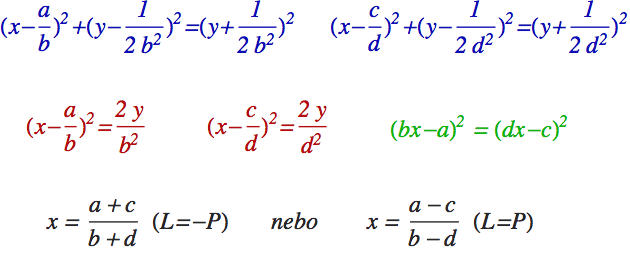
A teď už si jen uvědomíme, že pokud se dva zelené čtverce rovnají
(symbolicky L2 = P2), tak je buď levá závorka stejná
jako ta pravá (L = P), a nebo se závorka nalevo rovná minus závorce napravo
(L = -P). Odtud dostaneme dvě řešení, která jsou zapsána černě. To
první nám dá oranžovou kružnici (vidíte v něm oba zlomky „blbě
sečtené“), zatímco to druhé představuje kružnici červenou (která se
také dotýká obou kružnic a podlahy, takže není divu, že nám vyjde v řešení). Koneckonců máme kvadratickou rovnici, takže dvě řešení nás
nesmí překvapit.
Nakonec dosadíme právě spočítané x do jedné z těch červených rovnic a dopočítáme y. Je to jen trocha algebry, takže to nechám na vás, ale budete při tom v závěru potřebovat výše zmíněný vztah (ad - bc)2 = 1.
A to už je pro dnešek opravdu vše.
Článek je redakčně upravenou verzí blogového příspěvku na serveru
iDNES.cz. Publikováno s laskavým svolením autora.
Další díly a původní texty jsou dostupné na blogu Jana Řeháčka.
