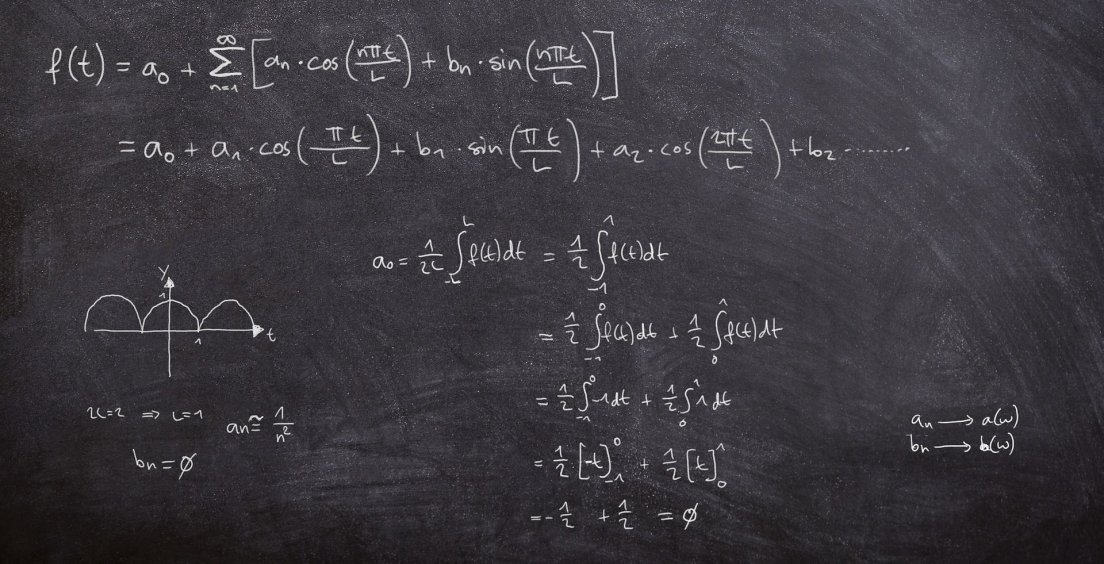U rovnice dítě stálo, z plna hrdla křičelo. Tak nějak si výuku matematiky představuje většina populace. A právem. Soustavy lineárních rovnic jsou od nepaměti obávaným strašákem středoškoláků, kteří by raději hřešili, než řešili.
Víte, proč říkáme „jedu DO Polska, Rakouska či Norska“, ale „jedu NA Slovensko“? Nevíte? No přece proto, že jazyk nemá logiku. Zatímco matematik si své věty a definice hezky seje do pečlivě narýsovaných brázd, čeština roste jako dříví v lese a svá semínka si v džungli gramatiky rozhazuje, jak se jí (nebo větru) zrovna zlíbí. Tu něco vypučí, tamhle se něco ujme a výsledkem je ten báječný dešťový prales, který s očima otevřenýma dokořán labužnicky procházíme a žasneme, jak jsme se tenhle jazyk vůbec mohli naučit.
Při tom divokém způsobu setby se tu a tam stane, že se v jazyce objeví díra. Ukáže se, že v podrostu bučiny existují holinky, kam zkrátka žádné semínko nenalétlo. Anebo že tam nalétlo nějaké, které nemělo.Vezměme si třeba dvojici sloves „řešit“ a „hřešit“. Pokud hřešíme, pak výsledkem našeho snažení je hřích. My matematici trávíme značnou část svých životů tím, že řešíme. Ale myslíte, že nás matička čeština za toto bohulibé úsilí odmění nějakým tím „říchem“? Kdepak. Ani ťuk. A pokud bychom se chtěli nazvat „říšníky“, vypadali bychom spíše jako poblázněný spolek přátel římského impéria. Semínka jazyka si prostě klíčí, jak chtějí.
A přitom se mi kolikrát stane, že na nějaké nerozorané mezi matematického velkostatku objevím šťavnatý trs lineárních rovnic. Pěkně si tam roste a čeká, až ho někdo vyřeší. Jak by bylo na světě krásně, kdybych si v takovém okamžiku mohl pomyslet: „To je ale fikaná lineární soustava, ta by, panečku, stála za řích.“
Lineární soustavy
Tak se na nějakou jednoduchou soustavu rovnou podívejme:
x - 3y = 2
-2x + y = 1
Hledáme zde dvě neznámá čísla x a y splňující výše uvedené vztahy.
Protože rovnice fungují jako misky vah, můžeme obsah té první dvojice misek dvakrát přihodit ke druhé a rovnováha zůstane zachována. Technicky řečeno: k druhé rovnici přičteme dvojnásobek první, a tím se zbavíme první neznámé:
-5y = 5
To už je jedna rovnice pro jednu neznámou, kterou lehce vyřešíme (y = -1) a z první rovnice pak dopočítáme zbytek (x = -1).
Na tomto místě bych rád vypíchnul, že je naprosto jedno, jak jsme své neznámé pojmenovali. Klidně jsme jim mohli říkat r a s nebo Karel a Petr. Rovnice by se pak daly přepsat jako:
Karel - 3 Petr = 2
-2 Karel + Petr = 1
ale řešení bude stále stejné: Karel i Petr se rovná -1.
Tím se dostáváme k první důležité abstrakci lineární algebry. Vzhledem k tomu, že na jménu proměnných nezáleží, při řešení rovnic s sebou nemusíme tahat všechna ta písmenka, ale bohatě stačí, když budeme upravovat pouze koeficienty.
Ta předchozí rovnice se tedy v abstraktním (maticovém) tvaru zapíše
1 -3 | 2
-2 1 | 1
Tomu, co je před oddělovníkem „|“, se říká matice soustavy, to, co je za ním, je vektor pravé strany a celé dohromady se to jmenuje „rozšířená matice soustavy“. Místo rovnic se spoustou neužitečných písmenek šibujeme pouze s řádky této matice.
Ta první úprava výše tuto rozšířenou matici převede na jednodušší tvar:
1 -3 | 2
0 -5 | 5
a z druhé řádky (rovnice) už je to řešení opět vidět.
Tato jednoduchá manipulace je základem jedné z nejběžnějších metod řešení větších soustav lineárních rovnic: vezmeme si to číslo vlevo nahoře (tedy na maticové pozici 1-1) a s jeho pomocí vynulujeme první sloupec (tak, že k ostatním řádkům přičítáme násobky jiných řádků - nejprve toho prvního). Pak si vezmeme číslo na pozici 2-2 a s jeho pomocí vynulujeme druhý sloupec. A takto pokračujeme dále, až máme pod hlavní diagonálou (tedy pozicemi i-i) samé nuly.
Úplně triviální to není, protože se občas stane, že číslo, pomocí kterého bychom chtěli provádět úpravy, je nula (a pak musíme rovnice – tedy řádky – trochu proházet), ale základní myšlenka je jasná. Pomocí elementárních úprav se snažíme rovnice (tedy řádky rozšířené matice) nahradit jednoduššími ekvivalenty, které se pak v závěru dají vyřešit „z ruky“.
Tomuto procesu se říká „Gaussova eliminace“ a vede k tzv. schodovitému (či odstupňovanému) tvaru soustavy, ze kterého se dá řešení, jakož i geometrická struktura matice, lépe vypozorovat.
Zatímco rozšířená matice je výborná pro praktické počítání, pro teoretický vhled do mechaniky řešení se lépe hodí geometrický rámec z minulého Matykání, kdy se na matice díváme jako na zobrazení.
Vezměme si rovnice:
2Manon + 2Frufru = 4
Manon + Frufru = 2
(pro počestné občany: 2x + 2y = 4, x + y = 2)
Pokud si označíme matici soustavy A = ((2,2),(1,1)) a vektor pravé strany b = (4,2), pak hledáme vektor u = (x,y), takový, že A.u = b.
Matice A má rozměr 2 x 2 a reprezentuje tedy zobrazení z R2 do R2.
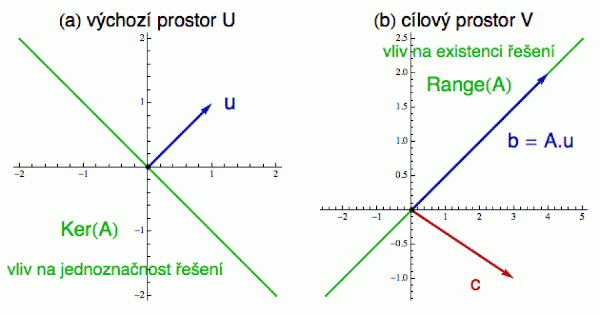
Můžete si každý vektor u vlevo představovat jako balistickou raketu, kterou matice A odpálí (přenese) do bodu A.u nacházejícího se v nepřátelském území vpravo. Při řešení se vlastně ptáme, odkud musíme raketu u odpálit, aby zasáhla nepřátelský vektor b.
Minule jsme si řekli, že každý z obou prostorů obsahuje jeden důležitý podprostor (na obrázku jsou vyznačeny zeleně).
Prostor U obsahuje nulový podprostor Ker(A), tedy množinu vektorů, které se zobrazují do nuly (A.u = 0), zatímco cílový prostor obsahuje obor hodnot Range(A), což jsou v podstatě lineární kombinace sloupců matice A. Ten Range si lze představit také jako množinu všech vektorů ve V, které lze „zasáhnout“ z území U pomocí raket naváděných maticí A.
Tyto podprostory nám pomohou určit, kdy řešení existuje a kdy je jednoznačné. Vezměme si vektor h∈Ker(A) splňující A.h = 0 (této rovnici se říká homogenní soustava určená maticí A a dostaneme ji tak, že vektor pravých stran nahradíme triviálním vektorem, skládajícím se z příslušného počtu nul). Tento vztah de facto popisuje, které rakety z prostoru U zasáhnou počátek prostoru V. Libovolný vektor h z podprostoru Ker(A) můžeme přičíst k nalezenému řešení nehomogenní soustavy A.u = b a dostaneme další řešení: A.(u + h) = A.u + A.h = A.u = b. Pokud je tedy nulový podprostor netriviální (obsahuje alespoň jeden netriviální vektor), pak naše původní (nehomogenní) soustava nemá jednoznačné řešení.
Obor hodnot (zelený podprostor vpravo) naopak umožňuje vyšetřit, zda vůbec nějaké řešení existuje. Pokud je vektor b součástí tohoto podprostoru, řešení problému A.u = b existuje. Pokud ne (jako např. vektor c), příslušná soustava (A.u = c) řešení nemá (pouze ta zelená přímka se dá z „území“ U zasáhnout raketami).
V našem konkrétním příkladu Manon-Frufru je Range(A) množina všech kombinací sloupců (2,1) a ještě jednou (2,1), což je přímka určená vektorem (2,1). Vektor b = (4,2) na ní leží (to je dost klika) a tím je existence řešení zaručena (něco z prostoru U tenhle vektor určitě zasáhne). Kdybych vektor b posunul mimo zelenou přímku (třeba do pozice c), řešení by neexistovalo.
Jednoznačnost řešení ovšem čekat nemůžeme, protože nulový prostor (a to je nutno spočítat z definice) je tvořen násobky vektoru h = (1,-1). Ke každému řešení rovnice A.u = b (jedno partikulární řešení je např. u = (1,1)) tedy můžeme takový násobek přičíst a stále to bude naši soustavu řešit.
Obecné řešení je v podstatě posunutý nulový prostor a v našem případě ho můžeme zapsat jako u = (1,-1) + t(1,1), kde t je zmíněný násobek, tj. libovolné reálné číslo. Nulový prostor je zde 1D, takže jsme přirozeně dostali 1 volitelný parametr v obecném řešení. Pokud by nulovým prostorem byla rovina, dostali bychom 2 atd.
Existence nulového prostoru se hodí, pokud na naše řešení chceme naložit další podmínky. Např. budeme-li požadovat, aby leželo na ose x (tj. y = 0). Z obecného řešení vidíme, že musíme najít t splňující -1 + t = 0. Takže t = 1 a partikulární řešení ležící na ose x bude u = (1,-1) + 1(1,1) = (2,0).
Možná namítnete, že celá tahle podprostorová šaráda se dala odhadnout selským rozumem, protože druhá rovnice je prostě násobkem té první. To je pravda. Ale pokud budete mít 7 rovnic se 7 neznámými, tak tam už ta existence a jednoznačnost tak jasná nebude, protože vnitřní strukturu matice A jen tak lehce neprokouknete.
Většinu černé práce za vás dnes sice udělají počítače, které vám ty podprostory prozradí, ale vy je musíte umět správně interpretovat. Mimochodem, u rovnice Karel-Petr je situace trochu jiná. Nulový prostor je zde triviální (řešením homogenní rovnice je pouze triviální vektor (0,0)), takže o jednoznačnost je postaráno. Existence také není problém, protože oborem hodnot je zde celý prostor V, takže libovolný vektor b se dá z území U zasáhnout.
Zajímavé je, že v okamžiku, kdy jsme tu všeobecnou existenci ztratili (obor hodnot se smrskl z 2D pro Karel-Petr do 1D pro Manon-Frufru), tak jsme ztratili i jednoznačnost (nulový prostor zbytněl z 0D na 1D). To není náhoda, ale jedna z velmi důležitých vět lineární algebry, která říká, že:
(*) dim Ker(A) + dim Range(A) = dim U
tj. součet dimenzí obou zelených podprostorů je roven dimenzi výchozího
prostoru.
Pokud tedy dimenze range(A) klesne (existence řešení se stane problematickou), tak musí současně vzrůst dimenze nulového prostoru (a tím pádem ztratíme i jednoznačnost). Jako by ty dimenze měly společný rozpočet. Když tady uberete, tak tamhle musíte přidat. Zjistíme-li, že range(A) má stejnou dimenzi jako výchozí prostor U (jako je tomu v případě Karel-Petr), tak už nulový vektor nemusíme počítat, protože předchozí věta nám zajišťuje, že bude 0D (bude to pouze triviální vektor sedící v počátku).
V této sekci jsme řešili dvě rovnice pro dvě neznámé (matice A byla typu 2x2). Obecný případ, kdy máme m rovnic pro n neznámých, se dá zasadit do stejného rámce (matice A bude typu mxn). Prostor U bude n-dimenzionální, prostor V m-dimenzionální.
Matice obdélníkové
(tuto sekci můžete v případě ohrožení života přeskočit)
Než se začneme montovat do čtvercových matic (typu nxn), podívejme se ve stručnosti na dva patologické případy: na soustavy nedourčené, kdy máme více neznámých než rovnic (m<n), a na soustavy přeurčené (m>n), kdy máme naopak více rovnic než neznámých.
V případě nedourčených soustav je obdélníková matice „naležato“ a výchozí prostor U má vyšší dimenzi než cílový prostor V. Báze prostoru U, skládající se z n vektorů, dokáže v typickém případě „vyplnit“ cílový prostor V, takže s existencí většinou problémy nejsou. Z věty o dimenzi (*) pak ale vyplývá, že dostaneme netriviální nulový prostor (protože dim Range(A) nemůže být větší než dimenze cílového prostoru V), takže řešení nebude jednoznačné. Stejně jako u soustavy Manon-Frufru dostaneme parametrické řešení, kde počet parametrů odpovídá dimenzi nulového prostoru (viz parametrická rovnice přímky, roviny či nějakého komplikovanějšího podprostoru).
Úmyslně jsem použil slovo „typický“, protože i v nedourčeném případě by se nám mohlo stát, že sloupce matice A (tedy obrazy bázových vektorů prostoru U) prostor V nevyplní (představte si třeba, že všechny sloupce leží v jedné přímce, tj. jsou kolineární) a pak můžeme mít i v tomto případě problémy s existencí (pokud nám vektor b padne mimo tu přímku).
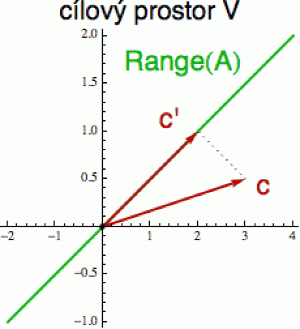
V případě přeurčených soustav je obdélníková matice „nastojato“ a výchozí prostor U má nižší dimenzi než cílový prostor V. Jeho báze, skládající se z n vektorů, v tomto případě nemá šanci „vyplnit“ cílový prostor V (např. kombinacemi dvou vektorů 3D prostor nikdy nevyplníte), takže Range(A) bude mít vždy nižší dimenzi než cílový prostor V. Těch n sloupců matice nám dá typicky n-dimenzionální podprostor m-dimenzionálního prostoru V (n < m). Tím slovem „typicky“ předpokládám, že sloupce jsou nezávislé. Pokud ne, tak bude Range(A) ještě o něco „hubenější“.
Protože Range(A) je v tomto případě jen malou částí cílového prostoru V, typický (náhodně vybraný) vektor b v něm nebude ležet a soustava A.u = b nebude mít řešení. V takovém případě můžeme zkusit vektor c promítnout do podprostoru V (na obrázku vpravo jsem tu projekci označil c') a jako náhradní řešení pak uvažovat rovnici A.u = c', která už řešení mít bude. Není to sice to pravý vořechový, ale nic jiného vám nezbývá. Takto můžete mimochodem nahlížet třeba na lineární regresi. Pokud se snažíte vést přímku více než dvěma body, máte přeurčený systém, protože od její rovnice očekáváte příliš mnoho. Metoda nejmenších čtverců pak de facto ten neposlušný vektor c „natlačí zpátky“ do podprostoru Range(A), tj. promítne ho do vektoru c'.
I tato analýza by se v podstatě dala udělat selským rozumem. Přeurčené systémy kladou na proměnné příliš mnoho podmínek, a tak typicky nemají řešení. Nedourčené zase proměnné nedokážou dostatečně svázat, takže si řešení běhají po podprostoru pomocí parametrů, místo aby slušně seděla na jednom místě.
Musíme mít ale stále na zřeteli, že slovo „typicky“ není radno přeceňovat. I přeurčený systém může mít řešení (pokud se vektor b „trefí“ do podprostoru range(A)). A nedourčený systém nemusí mít žádné řešení, jak jsem naznačil výše.
Např. systém x + y + z = 1 a 2x + 2y + 2z = 3 je nedourčený, ale řešení nemá. Range(A) je zde přímka určená vektorem (1,2) a vektor b = (1,3) na ní prostě neleží a neleží.
Jinými slovy, ty „typické“ případy nám dají jistou intuici pro to, jak se lineární systémy obecně chovají, ale v konkrétních případech musíme vždy (třeba i za pomoci počítačů) vyšetřit charakter obou „zelených“ podprostorů.
Matice čtvercové
V praxi se nejčastěji setkáváme s maticemi čtvercovými, které odpovídají situaci, kdy máme n rovnic pro n neznámých.
V tomto případě si musíme pohlídat, zda se n bázových vektorů z výchozího prostoru zobrazí na vektory lineárně nezávislé (což je – opět ve smyslu náhodného výběru – typický případ). Pokud ano, tak se z nich dá zrekonstruovat celý cílový prostor, což znamená, že řešení systému A.u = b existuje pro každou pravou stranu b (obor hodnot Range(A) má dimenzi n). Z věty o dimenzi (*) vyplývá, že nulový prostor má dimenzi 0 (dim U - dim Range(A) = n-n = 0) a je to tedy pouze triviální vektor. Každé řešení je tedy jednoznačné.
Pokud jsou obrazy bázových vektorů (tj. sloupce matice A) lineárně závislé, pak nastanou potíže. Range(A) bude pouze podprostor menší dimenze než n a pro vektory b, které se do něj nevejdou, řešení existovat nebude. Současně z věty o dimenzi vyplyne, že nulový prostor bude mít dimenzi alespoň 1, takže řešení (pro vektory b, které se do Range(A) vejdou) nebude jednoznačné. Tyto dvě eventuality rozdělují čtvercové matice na regulární a singulární.
Čtvercové matice mají celou řadu speciálních vlastností, protože výchozí i cílový prostor má stejnou dimenzi (můžete si představit, že matice A operuje na jednom a tom samém n-dimenzionálním prostoru).
Minule jsme viděli, že pro ně můžeme definovat vlastní čísla a v některých případech i tzv. inverzní matici A-1, která splňuje rovnici
A.A-1 = A-1.A = I
(kde I je jednotková
matice)
Pokud takovou matici máte, můžete soustavu A.u = b vynásobit (zleva) inverzní maticí a řešení pak dostanete obratem ruky: u = A-1.b
K nejzajímavějším charakteristikám čtvercových matic patří determinant. Značí se svislými čarami – anebo prostě det(A) – a je to skalár (obvykle reálné číslo), který z dané matice A obdržíme následujícím způsobem (na obrázku je ilustrace pro typ 5x5). Z prvního řádku si vybereme nějaké číslo (červeně) a vyškrtneme příslušný sloupec. Pak si na druhém řádku z nevyškrtnutých sloupců vybereme další prvek a jeho sloupec také vyškrtneme. A takto pokračujeme, až získáme n čísel, z každého sloupce i řádku právě jedno.

Takový výběr odpovídá permutaci n čísel (bez opakování). V našem případě je to permutace (21354). Na prvním řádku jsme si vybrali druhý sloupec, na druhém první, na třetím třetí, na čtvrtém pátý a na pátém čtvrtý. Pokud bychom si vybrali čísla na hlavní diagonále, zaznamenali bychom je triviální permutací (12345). No a teď ta zakroužkovaná čísla pronásobíme a výsledné součiny (ten na obrázku je -72) sečteme pro všechny možné permutace (tedy přes všechny možné výběry, kde z každého řádku i sloupce vybíráme právě jeden prvek). A aby to nebylo tak jednoduché, tak liché permutace vezmeme s opačným znaménkem (de facto je odečítáme), zatímco permutace sudé vezmeme tak, jak jsou. Determinant matice na obrázku je tedy roven 208 (ale pokud nejste pojištěni, raději ho takhle nepočítejte).
Permutace se dělí na sudé a liché podle toho, kolik transpozic (prohození) musíme udělat, abychom ji dostali z té triviální. Tu naši červenou (21354) dostaneme z té triviální (12345) prohozením 1 a 2 a následným prohozením 4 a 5. Potřebovali jsme tudíž dvě prohození (transpozice), takže naše permutace je sudá. Při výpočtu determinantu bychom tedy příslušný součin -72 vzali tak, jak je.
Pro malé matice se tato definice dá přeformulovat a zjednodušit. Pro matice typu 2x2 existují pouze dvě možné permutace. Triviální (12), která je sudá (má 0 transpozic), a pak jedna netriviální (21), která je lichá (neb obsahuje jednu transpozici – prohození 1 a 2). Matice A = ((a,b),(c,d)) má determinant a * d – b * c. První člen pochází z první permutace a druhý z druhé (a protože je lichá, změnili jsme mu znaménko).
Pro matice 3x3 se výpočet ještě dá ošulit pomocí různých speciálních pravidel, ale pro vyšší typy už je nalezení determinantu recept na akutní bolest hlavy. Obvykle se počítá tak, že se pomocí různých rozvojových formulek převede na výpočet několika determinantů nižší dimenze. Anebo se dá spočítat šalamounsky naprogramovaným počítačem (pokud ho máte, tak si jako zajímavůstku můžete ověřit, že determinant je součinem všech vlastních čísel matice).
Na první pohled by se mohlo zdát, že taková šílená definice nemůže mít žádné kloudné vlastnosti. Ale opak je pravdou. Determinant det(A) patří k nejužitečnějším nástrojům lineární algebry.
Jednak má zajímavé algebraické vlastnosti, platí například, že determinant součinu matic je součinem jejich determinantů: det(A.B) = det(A).det(B). A jednak má zajímavé geometrické vlastnosti: když si ze sloupců matice A sestavíte pravidelný rovnoběžnostěn, pak jeho objem bude roven absolutní hodnotě determinantu matice A. Takový výpočet je kupodivu rychlejší než pracně počítat různé výšky a podstavy.
A má i spoustu praktických aplikací. Například čtvercové lineární soustavy s regulární maticí se dají poměrně rychle vyřešit pomocí Cramerova pravidla. Rovnice A.u = b má explicitní řešení
ui = det(Ai)/det(A)
kde Ai je matice, která vznikne nahrazením i-tého sloupce matice A vektorem b.
A v neposlední řadě nám determinant umožňuje rychle rozhodnout, zda je daná (čtvercová) matice regulární, nebo singulární.
Je to vlastně zázrak, že jedno jediné číslo dokáže tak dovedně v kostce charakterizovat celou matici.
Matice regulární a singulární
Každý dobrý film má své klaďasy a hříšníky. A mají je i matice (tím ovšem netvrdím, že by se skripta z lineární algebry měla zfilmovat – to by se asi na Barrandově musel vyhlásit stav ohrožení – i když z Gaussovy eliminace by se možná detektivka udělat dala - já bych se kupříkladu s chutí podíval, jak pan rada Vacátko počítá algebraický doplněk v adjungované matici)
V minulé sekci jsme viděli, že o vlastnostech soustav n rovnic s n proměnnými rozhoduje, zda se jejich maticím při zobrazování bázových vektorů podařilo uchovat jejich nezávislost. Pokud ano, s existencí řešení ani s jeho jednoznačností nejsou potíže. Takovým maticím se říká regulární. To jsou klaďasky. Pokud ne, musíme při řešení našlapovat velmi opatrně. Příslušným maticím pak říkáme singulární a ty hrají roli hříšnic.
Singularita matice je výrazem určitého defektu. Jeho velikost můžeme – jak jsme minule nakousli – kvantifikovat dimenzí oboru hodnot (hodnost matice se často značí anglickým slovem „rank“, které přímo evokuje pozici ve vojenské hierarchii). Pokud má Range(A) dimenzi n, matice má plnou hodnost. Čím je hodnost nižší, tím je matice „defektnější“ (v tom smyslu, že kombinace jejích sloupců dokáže zrekonstruovat menší a menší část prostoru V).
Zajímavé je, že tu hodnost můžeme poměřovat jak lineárními kombinacemi sloupců, tak lineárními kombinacemi řádků a v obou případech dostaneme stejné číslo (tj. stejnou dimenzi) – což je další z fundamentálních vět lineární algebry.
(Ještě zajímavější je, že o hodnosti se ve své nekonformní učebnici života zmiňuje i Jára Cimrman, byť v trochu jiném významu. V úvodu závěrečné kapitoly poznamenává: „Manon i Frufru dnes byly mimořádně milé a vstřícné. Až je mi ta jejich hodnost podezřelá.“)
Matice mají celou řadu vlastností a demarkační linie mezi klaďaskami a hříšnicemi se táhne napříč jejich výčtem jako hraniční příkop. Hříšnice jsou hříšnicemi ve všech aspektech a klaďasky naopak. Následující tabulka podává stručný souhrn nejběžnějších rozdílů mezi oběma typy matic (pro určitost budu předpokládat, že jsou typu nxn a operují na prostoru U).

(matice soustavy Karel-Petr je regulární, Frufru-Manon je
singulární)
Zhruba se dá říci, že singulární matice suplují roli 0 ve vícerozměrném kontextu. Rozdíl mezi singulárními a regulárními maticemi je podobný jako rozdíl mezi nulou a nenulovými čísly na reálné ose (každé číslo je vlastně matice 1x1). Nula je zde hříšníkem a libovolné nenulové číslo klaďasem. Spoustu výše uvedených vlastností lze přímo přeložit do jazyka reálné osy, což můžeme použít jako mnemotechnickou pomůcku.
Začneme třeba tím, že nula jako jediné číslo nemá svůj inverzní prvek (vlastnost 9), protože 0-1 = 1/0 neexistuje, zatímco třeba 3-1 = 1/3. Homogenní rovnice ax = 0 má pro nenulové číslo a pouze triviální řešení (vlastnost 7), zatímco pro a = 0 má řešení nekonečně mnoho (každé reálné číslo). Nehomogenní rovnice ax = b má pro nenulové číslo a řešení pro každé b (vlastnost 4), zatímco pokud je a = 0, pak má řešení jen pro jednu velmi speciální hodnotu b (b = 0).
Za domácí cvičení si můžete rozmyslet, jaký je nulový prostor Ker(a) a obor hodnot Range(a), pokud se na to číslo budeme dívat jako na lineární zobrazení z R1 do R1 dané formulkou y = ax.
Článek je redakčně upravenou verzí blogového příspěvku na serveru iDNES.cz. Publikováno s laskavým svolením autora. Další díly a původní texty jsou dostupné na blogu Jana Řeháčka.