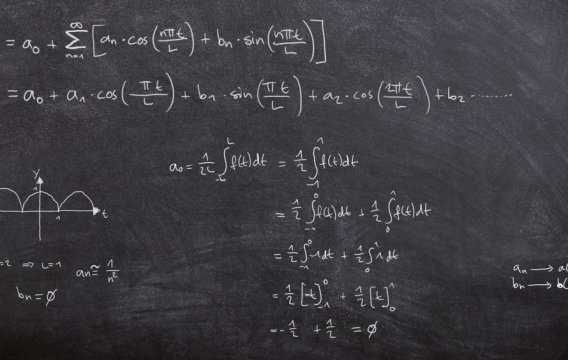Uprostřed 18. století se presbyteriánský duchovní Thomas Bayes zabýval statistickými aspekty existence zázraků. Při tom narazil na zajímavé tvrzení, které se ironií osudu stalo výchozím bodem pro naši cestu k umělé inteligenci.
Tchoř Šuperka se vracel z parfumerie v dobrém rozmaru. Konečně mu objednali Chanel No. 5 v průmyslové koncentraci. Když dorazil ke stoleté lípě, stezička domů se rozdvojila na dvě zhruba stejně dlouhé větve a Šuperka si jako obvykle jednu z nich zcela náhodně vybral. Dnes zvolil pravou a to neměl dělat. Odkudsi zpoza pařezu se vynořila neviditelná ruka nadhozu a pic-ho, majzla Šuperku dřevěnou paličkou po hlavě. Tchoř otupěle zavrávoral, pacičkou zatápal kolem sebe, ale po chvíli se oklepal a pokračoval dál. Prvních pár dní příhodě nevěnoval pozornost - koneckonců neštěstí nechodí po lidech, ale po tchořích - ale když ho asi za měsíc opět klepla palička a opět v pravé větvi stezky, někde v jeho lasicovitém mozku se rozsvítila žárovička a od té doby začal při návratu z parfumerie preferovat levou větev.
Tak nějak si představuju reakci inteligentního organismu. Všichni máme v hlavě určitý model reality, který nám umožňuje v tomto bizarním a mnohdy záludném světě jakž takž přežít. Ten model ale není neměnný. Každý den ho konfrontujeme s novými poznatky a pozorováními. Známkou inteligentního života je, že na jejich základě dokáže svůj vnitřní model reality pružně pozměnit, či dokonce radikálně překopat, pokud se od něho nová data význačně odlišují. Naše adaptabilita je nutností nejen proto, že své prostředí v průběhu života stále lépe poznáváme, ale i proto, že ono se samo o sobě mění. Fungovat na bázi nějakého neměnného algoritmu by bylo vběhnutím na slepou větvičku evoluce.
Pokud budeme chtít vymyslet umělou inteligenci, musíme ji především naučit, jak se učit (machine learning), tedy jak se přizpůsobit měnícím se podmínkám a jak efektivně reagovat na nová data, ať už budou pocházet ze smyslových sensorů robota, anebo z aktuálních vstupů nějakého softwaru.
Jedním z mechanismů, který takovou aktualizaci umožňuje, je Bayesova věta - matematické tvrzení, které ve svých důsledcích ukazuje, jak měnit parametry statistického modelu v závislosti na pozorovaných datech. Tak dalekosáhlé aplikace reverend Bayes ve své době nemohl samozřejmě tušit. V jeho bádání šlo spíše o elementární pravděpodobnostní úvahy, pomocí kterých se pokoušel přijít na kloub nejrůznějším zázrakům.
Thomas Bayes vystudoval logiku a teologii a k pravděpodobnosti se dostal až v závěrečné fázi svého života. Jeho zápisky posmrtně utřídil Richard Price a v roce 1763 je vydal ve sborníku skotské královské akademie věd. Bayesovo dědictví dlouhou dobu přežívalo jen v zaprášených učebnicích statistiky. Teprve ve druhé polovině 20. století, v souvislosti s rozvojem výpočetní techniky, se jeho věta stala základem bouřlivě se rozvíjejících kvantitativních metod. Kdyby se dnes Thomas Bayes zúčastnil nějaké moderní konference o strojovém učení a slyšel své jméno v každé druhé přednášce, asi by to považoval za zázrak (mimochodem, aby si pan reverend přišel na své, v sekci „Frekventisté versus bayesiáni“ se podíváme, jaká je vlastně pravděpodobnost, že existuje Bůh).
Podmíněná pravděpodobnost
Věci se nejlépe posuzují v kontextu. Tisícovka nalezená na chodníku bezdomovcem má cenu zlata, zatímco pro průměrného miliardáře nestojí za ohnutí hřbetu. Zatím jsme se na pravděpodobnost dívali jako na absolutní číslo zhruba vyjadřující poměrnou četnost daného jevu při dostatečně mnoha opakováních. To je náhled postačující pro trápení studentů u maturitních písemek, ale v praxi často potřebujeme vědět, jakou máme šanci na úspěch ne v nějakém abstraktním absolutnu, ale ve zcela konkrétních podmínkách.
Farmáře nezajímá, jaká je obecná pravděpodobnost dobré sklizně, ale jaká je šance na plnou stodolu v případě mimořádně suchého jara. Kuřáka nezajímá, jaká je pravděpodobnost plicních komplikací v běžné populaci, ale jak si v tomto ohledu stojí vyznavači nikotinu. Pokud si vyberete náhodný blog a zeptáte se, jaká je pravděpodobnost, že v něm najdete slovo „banka“, zjistíte, že je to zhruba 2.5 %. Pokud se ovšem omezíte pouze na blogy obsahující slovo „finanční“, zjistíte, že ta samá pravděpodobnost najednou vyskočí na 14 %. Kontext dokáže podstatně změnit výsledek.
Pravděpodobnosti nějakého jevu A, za předpokladu, že nastal jev B, se říká podmíněná pravděpodobnost a značí se svislicí "|": P(A | B). Pravděpodobnost, že mi při hodu kostkou padne šestka, je 1/6. Pokud vám ale prozradím, že mi padlo sudé číslo, pak pravděpodobnost šestky vzroste na 1/3 (protože už existují jen tři rovnocenné možnosti: 2, 4, 6). Takže symbolicky (ať si zvykneme na notaci):
P(šestka | sudé) = 1/3
Podmíněnost bychom samozřejmě mohli také obrátit a zeptat se, jaká je pravděpodobnost, že nám padne sudé číslo, za předpokladu, že jsme hodili šestku.
P(sudé | šestka) = 1
Ta je v tomto případě triviální (100%), ale aspoň hned na začátku vidíme, že P(A | B) a P(B | A) jsou obecně dvě zcela jiné pravděpodobnosti.
To vidíme i ze schematického obrázku.
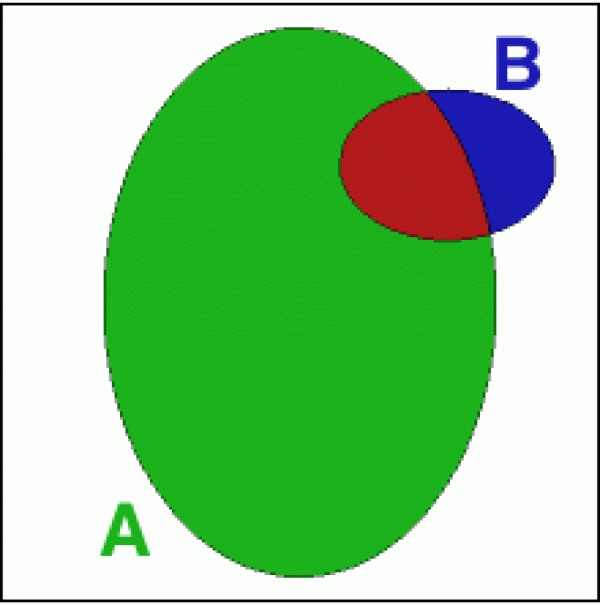
Představme si pravděpodobnost nějakého jevu jako plochu naznačené elipsy (a to není zase tak za vlasy přitažený náhled - ve vyšší matematice je pravděpodobnostní počet v jistém smyslu odnoží teorie míry, což je disciplína zabývající se počítáním obsahů a objemů).
Jev A má větší plochu (vzhledem k rámečku symbolicky reprezentujícímu „všechny možnosti“) a bude tedy pravděpodobnější než jev B.
V této reprezentaci se na pravděpodobnost P(A | B) můžeme dívat tak, že náš „vesmír“ (rámeček) všech možností zkolaboval do množiny B a všechny úvahy o jevu A budeme posuzovat pouze zevnitř této množiny. Jak se jev A chová mimo rámec množiny B, nemá na pravděpodobnost P(A | B) žádný vliv.
Nezajímá nás tedy plocha A vzhledem k celkovému rámečku (což by byla pravděpodobnost jevu A), ale pouze plocha vyseknutá množinou A uvnitř množiny B. Tedy jak velký je průnik (červený) vzhledem k celkové ploše B (modrá plus červená). Symbolicky si můžeme zapsat vzoreček pro podmíněnou pravděpodobnost takto:
P(A | B) = P(A a současně B) / P(B)
a nebo množinově pomocí průniku
(*) P(A | B) = P(A ∩ B) / P(B)
Opět vidíme přímo z geometrie obrázku, že P(A | B) a P(B | A) jsou dvě různá čísla - červená část zaujímá zcela jiný podíl obou množin.
Pokud se stane, že P(A|B) = P(A), tedy jev B pravděpodobnost A nijak neovlivní, tak říkáme, že jevy A a B jsou nezávislé. Z rovnice (*) potom vyplývá, že P(A ∩ B) = P(A) * P(B). Výše jsme viděli, že nález slova „banka“ v blogu a nález slova „finanční" nejsou nezávislé, protože jakmile najdeme slovo „finanční“, pravděpodobnost nálezu slova „banka“ se zvýší: P(banka | finanční) > P(banka). Budeme-li ale uvažovat, zda jméno blogera začíná na J, nebo ne, pak takový jev a nález slova „banka“ v blogu nezávislé budou, protože začáteční písmeno blogerova jména nemá na výskyt slova „banka“ v blogu žádný vliv.
Podívejme se ještě na jeden příklad.
Jako fotbalový fanoušek si vedete statistiky všech střel na bránu ve stávajícím ligovém ročníku a uvažujete následující dva jevy:
G - daná střela vedla ke gólu
J - daná střela byla „jedenáctka“ (tedy penalta)
Pak P(G | J) je pravděpodobnost gólu za předpokladu, že daná střela přišla z penalty (tedy že náhodně vybraná penalta povede ke gólu) - a ta je dost vysoká, odhadl bych ji tak na 70 %.
Na druhé straně P(J | G) je pravděpodobnost penalty za předpokladu, že daná střela vedla ke gólu (tedy že náhodně vybraný gól byl způsoben penaltou) - a ta je poměrně nízká, protože penalt se obecně moc nekope, odhadl bych ji na méně než 30 %.
V tomto případě tedy platí P(G | J) > P(J | G).
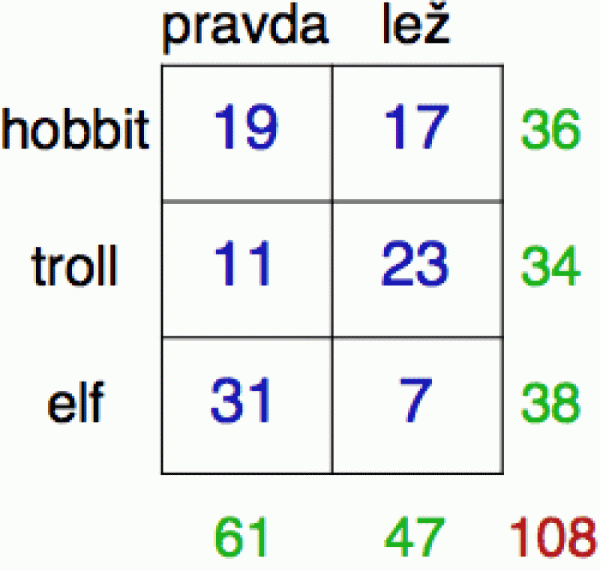
Výbornou pomůckou pro pochopení podmíněné pravděpodobnosti jsou tzv. kontingenční tabulky, které přehledně zaznamenávají empirickou četnost určitých jevů.
Představme si tabulku pravdivosti výroků pohádkových bytostí (viz vpravo). Pro každou z nich si zaznamenáme, zda mluvila pravdu či lhala, a souhrnné počty pro daný typ bytosti vyneseme do příslušného řádku (řádkové a sloupkové součty jsou v zeleném).
Vidíme, že elfové mluví většinou (ale ne vždy) pravdu, trollové obvykle lžou a hobiti to mají tak půl na půl.
Z tabulky si odhadneme všechny potřebné pravděpodobnosti.
P(troll) = 34/108 = 0.315
P(bytost lže) = 47/108 = 0.435
Nás budou zajímat podmíněné pravděpodobnosti. Tedy jak závisí sklon ke lhaní na typu bytosti:
P(lež | hobit) = 17/36 = 0.472
P(lež | troll) = 23/34 = 0.676
P(lež | elf) = 7/38 = 0.184 (to jsou pašáci!)
a opět se můžeme přesvědčit, že ta „inverzní“ pravděpodobnost je jiná.
P(troll | lež) = 23/47 = 0.489
což je de facto pravděpodobnost, že náhodně odchycená pohádková bytost je troll, za předpokladu, že nám u výslechu zalhala. Každá data, která získáme, nám umožňují přesnější odhad pravděpodobností. Když nám v pytli přinesli lapeného výtečníka, měli jsme 31.5% šanci, že je to troll. V okamžiku, kdy se z pytle ozvala lež, pravděpodobnost stoupla na 48.9 %.
Bayesova věta
V předchozí sekci jsme viděli, že podmíněná pravděpodobnost není symetrická, tj. P(A | B) a P(B | A) jsou dvě různé různé veličiny. Přesto jsou svázány poměrně jednoduchým vztahem prostřednictvím Bayesovy věty.
Na to, jak je pro moderní statistiku důležitá, se dá odvodit celkem jednoduše. Začneme tím, že si napíšeme definiční vztahy:
P(A | B) = P(A ∩ B) / P(B)
P(B | A) = P(A ∩ B) / P(A)
a uvědomíme si, že průnik, který obsahují, je stejný. Proto si ho z obou rovnic vyjádříme a porovnáme:
P(A | B) * P(B) = P(B | A) * P(A)
odtud pak prostým vydělením získáme Bayesův zákon, který nám umožňuje spočítat jeden typ podmíněné pravděpodobnosti z toho druhého („inverzního“).
(**) P(B | A) = P(A | B) * P(B) / P(A)
V praxi se k vyčíslení jmenovatele P(A) velmi často používá rozdělení na pravděpodobnost odpovídající jevu B a jevu komplementárnímu B':
(***) P(A) = P(A | B) * P(A) + P(A | B') * P(B')
To se hodí zejména tam, kde lze veličiny na pravé straně snadno spočítat ze zadání a de facto odpovídá množinové rovnosti
A = (A ∩ B) ∪ (A ∩ B')
(viz zelená a červená část na prvním obrázku)
V obecnějším případě se ve jmenovateli dá použít rozdělení všech jevů na N částí. Podívejme se na příklad.
Předpokládejme, že v populaci máme 10 % uživatelů nějaké drogy. Firma Farmaka vyvinula na tuto drogu poměrně spolehlivý test. Pro uživatele drogy vygeneruje v 98 % případů pozitivní nález, zatímco u neuživatelů ukáže v 95 % negativní nález (v prvním případě se tedy test „sekne“ pouze ve 2 % případů, ve druhém v 5 %).
Jaká je pravděpodobnost, že náhodně vybraný jedinec s pozitivním nálezem drogu skutečně užívá? Na první pohled by se mohlo zdát, že je to 98 %. Ale zdání klame.
Označme si pozitivní nález znakem „X“ a užívání, resp. neužívání drogy písmenky D a D' (jsou to jevy komplementární). Zajímá nás tedy pravděpodobnost, ze vybraný jedinec je uživatel, za předpokladu že jeho test byl pozitivni, tedy P(D|X).
Nejprve si zapíšeme Bayesovu větu v tomto značení:
P(D|X) = P(X|D) * P(D) / P(X)
Ve jmenovateli použijeme rovnici (***):
P(X) = P(X|D) P(D) + P(X|D') P(D')
Protože „uživatelů“ je celkově 10 %, „neuživatelů“ musí být 90 %, takže:
P(X) = .98 * 0.1 + 0.05 * 0.9 = 0.143
no a z Bayese dostaneme konečný výsledek
p(D|X) = 0.98 * 0.1 / 0.143 = 0.6853
Těch necelých 70 % je tedy trochu méně, než bychom očekávali.
Pochopitelně, pokud máte k dispozici kompletní kontingenční tabulku, všechny podmíněné pravděpodobnosti si lehce spočítáte přímo z ní. Máte-li ovšem k dispozici pouze neúplné informace, pak je Bayesova věta k nezaplacení. A abyste ji dostali opravdu „do ruky“, doporučuji si podle ní spočítat P(troll | lež) a porovnat to s výše uvedeným výsledkem.
V závěru předchozí sekce jsme viděli, že každá nová informace zpřesňuje náš pravděpodobnostní model světa. Na tomto fenoménu je založena reformulace Bayesovy věty, které se říká bayesovská inference (bayesovské odvozování či rozhodování).
Bayesovská inference
Ve statistice potřebujeme často ověřit platnost nějaké hypotézy H na základě obdržených dat D (nebo nějakého jiného důkazního materiálu). Pravděpodobnost získání takových dat za předpokladu platnosti hypotézy - tedy P(D|H) - se většinou spočítá snadno.
Bayesovu větu proto používáme pro výpočet obtížnější varianty, a to je P(H|D): jak je hypotéza H pravděpodobná za předpokladu, že jsme získali (ať už výpočetně či experimentálně) data D.
(****) P(H|D) = P(D|H) P(H) / P(D)
Tato rovnice se ve statistice používá tak často, že její členy mají své vlastní názvy.
P(H) se nazývá apriorní pravděpodobnost (angl. prior), protože vyjadřuje pravděpodobnost hypotézy před tím, než jsme vzali v úvahu získaná data.
P(H|D) na levé straně se označuje jako posteriorní pravděpodobnost (posterior) a odpovídá pravděpodobnosti hypotézy poté, co jsme vzali v úvahu data D.
P(D|H) je věrohodnost (likelihood) či věrohodnostní funkce. P(D) se říká marginální věrohodnost (marginal likelihood) nebo prostě pravděpodobnost modelu a je to de facto normalizační konstanta (tedy ve smyslu, že zaručuje normální chování posteriorní pravděpodobnosti - ne, že by ji vymyslel Gustáv Husák).
Podívejme se na příklad.

Máme dvě nádoby s modrými a červenými koulemi (viz obrázek), přičemž v nádobě A jsou dvě třetiny modrých koulí, zatímco v nádobě B jsou dvě třetiny červených. Nádoby jsou uzavřené a neoznačené.
Pravděpodobnost, že si z nádoby A vytáhneme červenou kouli, je tedy 1/3, zatímco pro modrou kouli jsou to 2/3 (a pro nádobu B obráceně).
Nyní si jednu z nádob náhodně vybereme a poté požádáme asistentku, aby z ní náhodně vybrala 10 koulí (přičemž každou vybranou zase vloží zpátky). To budou naše data D. Jak je naznačeno na obrázku vespodu, asistentka vytáhla 6 modrých koulí a 4 červené.
Selským rozumem bychom řekli, že na základě těchto dat jsme si pravděpodobně vybrali nádobu A. Bayesovská inference nám umožní tuto pravděpodobnost přesně vyčíslit.
Nejprve budeme potřebovat pravděpodobnosti vytažení daného kulového ansámblu D za předpokladu, že jsme je tahali z nádoby A, respektive B.
Protože v nádobce A mají modré koule pravděpodobnost 2/3, platí
P(D|A) = (2/3)^6 * (1/3)^4 = 0.00108
zatímco pro nádobku B dostaneme
P(D|B) = (2/3)^4 * (1/3)^6 = 0.00027
(viz analýza binomického rozdělení v této sekci Jauvajs, jen jsem zde potlačil binomický koeficient, který je v obou případech stejný a zkrátí se)
Výběr nádobky A a B jsou komplementární jevy (jednu si vybrat musíme), takže ve jmenovateli Bayesovy formulky můžeme použít stejný trik jako v předchozím případě.
P(A|D) = P(D|A) * P(A) / P(D) = P(D|A) * P(A) / (P(D|A) * P(A) + P(D|B) * P(B))
Počáteční (apriorní) pravděpodobnost výběru nádobky A bude 0.5, protože jsme vybírali zcela náhodně (hodili jsme si korunou). P(B) bude tím pádem také 0.5, takže tuto hodnotu vytkneme a zkrátíme
P(A|D) = P(D|A) / (P(D|A) + P(D|B))
a to je na základě předchozího výpočtu
P(A|D) = 0.00108 / (0.00108 + 0.00027) = 0.8
Po zohlednění dat jsme byli schopni pravděpodobnost výběru nádoby A zpřesnit z apriorních 50 % na posteriorních 80 %. Můžete si sami zkusit, jaký vliv na aktualizaci pravděpodobnosti bude mít jiný výběr koulí ze zvolené nádoby (další zajímavý příklad v angličtině najdete zde).
Většina náhodných veličin v sobě obsahuje určité parametry X (např. normální rozdělení obsahuje dva: průměr μ a rozptyl σ). Představme si, že máme generátor náhodných znaků, který generuje "A" s pravděpodobností X a "B" s pravděpodobností 1-X. Pokud známe parametr X, lehce si pro konkretní data D="ABBBAABAA" spočítáme podmíněnou pravděpodobnost P(D|X).
Bayesova věta nám i zde umožňuje zakousnout se do opačného problému. Máme určitá data D, ale nevíme, jak byl jejich generátor seřízen. Neznáme X. Bayesova věta nám ho sice neprozradí (to se u náhodných procesů ani nedá očekávat), ale pro každé X nám spočítá pravděpodobnost tohoto parametru pro obdržená data D, tedy P(X|D). V tomto případě má inferenční vzoreček tuto podobu:
P(X|D) = P(D|X) P(X) / P(D)
Jeho použití už je ale velmi technická záležitost (obzvlášť pro spojité proměnné, kde se musí ve jmenovateli namísto součtu integrovat), navíc X i D mohou být vektory, což formulce na jednoduchosti nepřidá, takže se v tomto místě s inferencí raději diskrétně rozloučíme.
Ještě se ale na chvíli vrátím k tchoři Šuperkovi - tedy k tomu, proč je bayesovská analýza základem mnoha metod směřujících k umělé inteligenci. Ať už jsme lidi, tchoři nebo roboti, náš vnitřní model (reprezentovaný, řekněme, hypotézou či nějakými parametry) má pro každý aspekt reality určitou apriorní pravděpodobnost. Na základě nově obdržených dat (rána paličkou do hlavy či výběr koulí ze zvolené nádoby) jsme schopni tuto hodnotu zpřesnit a dostat posteriorní pravděpodobnost. Propočítáním různých modelů si pak můžeme vybrat ten, který je vzhledem k získaným datům nejpravděpodobnější.
Tchoř Šuperka si riskantnost pravé stezičky aktualizoval z apriorního fifty-fifty na podstatně vyšší posteriorní hodnotu instinktivně (pochybuji, že Křemílek s Vochomůrkou holdují bayesovské statistice). Roboty to budeme muset naučit explicitně.
Frekventisté versus bayesiáni
Společnost je rozdělená, kam jen oko pohlédne. Levičáci versus pravičáci, horňáci versus dolňáci, sluníčkáři versus xenofobové, sparťani versus slávisti. A tak nás ani moc nepřekvapí, že i uvnitř statistiky zuří lítá válka mezi dvěma nesmiřitelnými tábory. O to, jak se vlastně dívat na pravděpodobnost, se už několik dekád přou frekventisté a bayesiáni. A přestože jejich spor má z velké části povahu interpretační, občas vede k odlišným numerickým výsledkům.
Zhruba řečeno, pro frekventistu je pravděpodobnost objektivní hodnotou, která ukazuje limitní chování četnosti daného jevu. Pro bayesiána je pravděpodobnost naopak subjektivní hodnotou, kterou můžeme v případě potřeby aktualizovat (zpřesňovat) zohledněním nových faktů či dat podle principů bayesovské inference.
To, jak jsme se zatím na pravděpodobnost dívali, byl v podstatě frekventistický náhled. Ovšem i ten bayesiánský má něco do sebe. Mnoho pravděpodobností, se kterými se v životě setkáme, má charakter subjektivního ohodnocení. Pokud řeknete „mám pocit, že je 60% šance, že Sparta zítra porazí Bohemku“, vyjadřujete tím pouze svůj subjektivní pocit, který by se jen těžko podepíral nějakou matematickou konstrukcí - i když vám nic nebrání si tu výslednou pravděpodobnost interpretovat frekventisticky: kdyby se hypoteticky dalo sehrát 100 utkání mezi Spartou a Bohemians v jejich zítřejších sestavách, zhruba v 60 z nich by vyhrála Sparta.
Pro frekventistu je tedy pravděpodobnost jakousi idealizovanou frekvencí daného jevu, zatímco pro bayesiána je spíše vyjádřením „stupně víry“ (degree of belief) v to, že daný proces bude mít daný výsledek.
A právě tento „stupeň víryL upoutal pozornost mnoha filosofů a teologů, kteří se bayesovské analýzy chytili v naději, že se jim podaří postavit náboženské pojmy na pevnější kvantitativní podklad. Kuriózní je, že reverendova věta je volána na lavici svědků jak pro důkaz existence Boha, tak pro jeho vyvrácení.
Abyste viděli, jakým způsobem se snaží zastánci vyšších sil namontovat Bayese do svých úvah, ukážu vám jeden příklad, který je založený na článku Joe Cartera: Pravděpodobnost Boha (The Probability of God) a v podstatě se opírá o stejnojmennou knihu Stephena Unwina. Holt, když pánbů dopustí, i matika spustí.
Jako základ našich úvah si vezmeme inferenční verzi Bayesovy věty (****) a k ní přidáme komplementární formulku (**), takže dostaneme (stejně jako v příkladu s nádobami)
P(B|A) = P(A|B) * P(B) / (P(A|B) * P(B) + P(A|B') * P(B'))
kde B je existence Boha, B' jeho neexistence a A je „argumentační podpora“.
Protože na pravé straně máme zlomek, můžeme ho „vykrátit“ výrazem P(A|B') a po zavedení pomocného „božího indikátoru“ (Divine Indicator Scale)
D = P(A|B) / P(A|B')
dostaneme z Bayesova vztahu tento vzoreček
(*****) P(B|A) = D * P(B) / (D * P(B) + 1 – P(B))
kde jsme využili komplementarity: tedy Bůh buď je, anebo není, nic mezi tím, což znamená, že P(B) + P(B') = 1. Hodnota P(B) je apriorní pravděpodobností (výše citovaný článek ji nazývá P-before), zatímco P(B|A) je pravděpodobností posteriorní (P-after).
Klíčovou proměnnou je tu samozřejmě „Déčko“, které autor interpretuje jako podíl pravděpodobností dané argumentace v případě, že Bůh existuje, respektive neexistuje.
Autor si pak vybere 6 argumentačních oblastí a subjektivně (!) pro každou určí, jaké to Déčko je. Pokud je např. D = 5, znamená to, že daný argument je 5x pravděpodobnější v případě existence Boha než v případě jeho neexistence. D = 0,5 zase znamená, že takovýto argument je o něco pravděpodobnější při neexistenci Boha.
Výpočet zahájíme s apriorním odhadem fifty-fifty (to samo o sobě je trochu kontroverzní), tj. P(B) = 0.5, a pak tuto pravděpodobnost 6x aktualizujeme podle formulky (*****), ale už s těmi subjektivně zvolenými Déčky, přičemž posteriorní (výstupní) pravděpodobnost z jednoho kroku je vždy vložena jako apriorní (vstupní) do kroku následujícího.
Tady je těch šest argumentů (i s jejich Déčky a v angličtině):
1. uznání všeobecného dobra (D = 10) recognition of goodness
2. existence morálního zla (D = 0.5) existence of moral evil
3. existence přírodního zla (D = 0.1) existence of natural evil
4. zázraky v rámci přírodních zákonů (D = 2) intra-natural
miracles
--- např. přítel se uzdraví, poté co se za něho modlíte
5. zázraky mimo rámec přírodních zákonů (D = 1) extra-natural
miracles
--- např. někdo mrtvý je vzkříšen
6. náboženské zážitky (D = 2) religious experiences
Když si tato Déčka postupně dosadíte do rovnice (*****) s tím, že začnete na 50 %, vyjde vám nakonec 66.666 % (takovejch šestek!), takže Bayesova věta podle Unwina „posiluje“ argument o existenci Boha (Carter s jeho hodnotami ovšem polemizuje a nahradí je svými vlastními, které mu napočítají pravděpodobnost boží existence dokonce 99%).
Alelůja!!! Nu, i tak se dá „aplikovat“ matematika.
Douška: Bayesovské sítě
Když jsem byl mladý, považoval jsem za téměř jisté, že se umělé inteligence nedočkám. Teď jsem podstatně starší a myslím, že je reálná šance, že se s ní potkám. Počítačoví experti se domnívají, že dosažení obávané singularity v průběhu první poloviny století je zhruba fifty-fifty (a to se zřejmě neobejde bez těžkých společenských a morálních dilemat).
Přesto patří umělá inteligence k bouřlivě se rozvíjejícím odvětvím, jak ve smyslu základního výzkumu, tak ve smyslu technologických aplikací. Na cestě od pasívních programů mechanicky vykonávajících zadané instrukce k plně autonomním androidům jsme urazili obrovský kus cesty. A přestože Turingův test stále odolává, dokážeme už sestrojit komponenty, které rozpoznávají předměty i řeč, dokáží se poučit z nově nabytých „zkušeností“ a jsou schopny vést primitivní komunikaci.
Protože modifikace vnitřního modelu reality na základě nových dat patří k základním znakům inteligence, není divu, že se s bayesovskou inferencí setkáváme i v jejích umělých pobratimech, od robotiky až po automatizované systémy. Která z mnoha cest nakonec zvítězí, se jen těžko odhaduje, ale protože v dnešním Matykání hraje prim reverend Bayes, zmíním se na závěr o bayesovských sítích.
Výpočet statistických parametrů bayesovskou inferencí je citlivý na množství vstupních dat. Problém nastane v okamžiku, kdy má studovaný systém tolik parametrů, že jejich přesné určení (obzvlášť pro velké datové soubory) začne představovat výpočetní obtíže. Náš model pohádkových bytostí obsahoval pouze jednu proměnnou (prolhanost) se dvěma hodnotami (lže/nelže). K dobrému statistickému modelu pro 3 bytosti by nám stačily 3 parametry - pravděpodobnost, že daný typ lže (a ty by se daly lehce odhadnout z kontingenční tabulky).
Pokud pracujete s N proměnnými a každá má dvě či více hodnot, musíte při aplikaci Bayesova zákona vzít v úvahu všechny možné kombinace. Počet parametrů pak roste exponenciálně s N. Bayesovské sítě umožňují při výpočtu pravděpodobností daného modelu vzít v úvahu pouze ty proměnné, které jsou v daném kontextu relevantní. Obvykle jsou definovány pomocí orientovaných acyklických grafů, pro které se používá anglická zkratka DAG (directed acyclic graph).
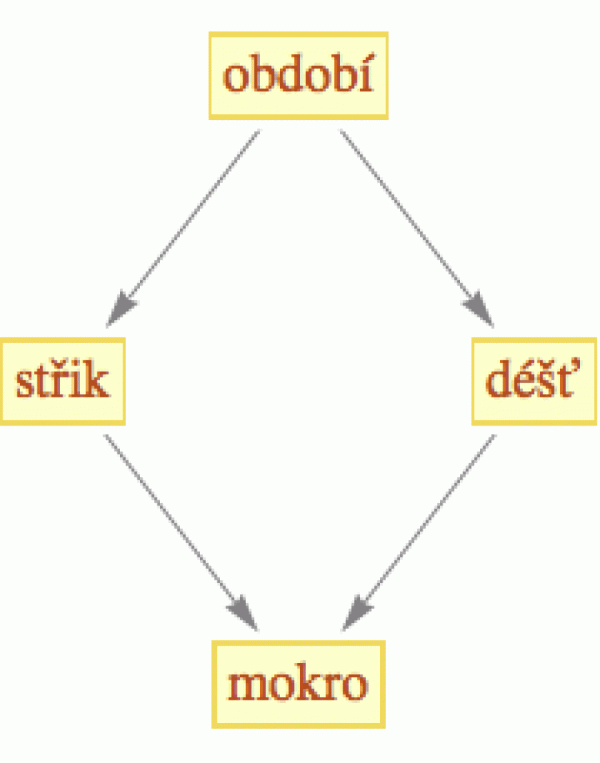
Sestavme si jednoduchý model, který popisuje, proč je trávník na zahradě mokrý (viz obrázek). Protože jsme právě instalovali nákladnou ostřikovací baterii, jsou pouze dvě možnosti: buď zavlažovač, a nebo déšť. Přitom jak zavlažovač, tak déšť závisí na období. V období vláhy bude vyšší pravděpodobnost na přirozených srážkách, v období sucha bude pravděpodobnějším zdrojem zavlažení umělý postřik.
Při výpočtu pravděpodobností našeho modelu si tedy nemusíme lámat hlavu, jaká je pravděpodobnost deště v závislosti na období, zapnutí zavlažovače a mokrosti trávníku (což by nám při binárních hodnotách dalo 8 možností), ale stačí nám odhadnout, jaká je šance na déšť v obou obdobích. To znamená, že nám k popisu stačí pouze 2 parametry:
P(déšť | období sucha) a P(déšť | období vláhy)
Zbývající proměnné - zavlažovač a mokrý trávník - déšť neovlivní (další příklady, včetně odhadu úspory parametrů, najdete v této pdf prezentaci).
Celá bayesovská inference, která by bez tohoto zjednodušení mohla mít stovky proměnných, je pak výpočetně daleko stravitelnější. To se hodí např. pro expertní diagnostické systémy, které se pokouší z rozsáhlých dat odvodit pravděpodobnosti různých nemocí v závislosti na pozorovaných symptomech (příslušná bayesovská síť pak může vypadat takto).
Kromě toho, že se dají snadněji interpretovat, mají bayesovské sítě ještě jednu výhodu. Podle některých odborníků mohou posloužit i pro určení kauzality, což je z praktického hlediska často důležitější než všechny podmíněné pravděpodobnosti světa (minule jsme například viděli, že korelace v žádném případě kauzalitu neimplikuje). Pokud vás tento aspekt zajímá, mrkněte se sem.
Článek je redakčně upravenou verzí blogového příspěvku na serveru
iDNES.cz. Publikováno s laskavým svolením autora.
Další díly a původní texty jsou dostupné na blogu Jana Řeháčka.