Dnes poklepeme na jeden z úhelných kamenů moderní matematiky - na pojem limity. Při té příležitosti nahlédneme pod kapotu spojitým funkcím a také se podíváme, co s tím vším má společného policie.

Matička příroda nemá ráda šoky. Preferuje spojitost a postupný přechod. Drtivá většina funkcí, se kterými se v praxi setkáme, její přání respektuje a má tu báječnou vlastnost, že pokud jen malilinko změníme vstupní hodnoty, hodnoty na výstupu se také o mnoho nezmění. Bez toho by byl život na této planetě hotovým martýriem. Vezměme si třeba takovou teplotní rozpínavost. Ze školních škamen si pamatujeme, že teplem se kolejnice roztahují, ale je to naštěstí jev velmi pozvolný. S každým stupněm se kolejnice prodlouží jen o chloupek. Jen si považte to pozdvižení na vsi, kdyby se při přechodu z teploty 24,67 °C na 24,68 °C kolejnice najednou prodloužila o celý metr. Z toho by chudáci strojvedoucí dostali minimálně žaludeční vředy. Náhlé skokové změny nejsou žádoucí a v přírodě se s nimi díky umírněným fyzikálním zákonům v podstatě nesetkáme.

Spojitosti vděčíme i za to, že můžeme v dalekohledu pozorovat dráhu zajíce hopkajícího po poli. Jeho poloha - jako funkce času - je také spojitá. Změní-li se čas jen o pár vteřin, zajícova poloha se změní maximálně o pár metrů, takže hopsálek nevypadne z našeho zorného pole a my máme šanci přizpůsobit směr dalekohledu jeho nové poloze. Kdyby se poloha zajíce změnila během jedné vteřiny, řekněme, o sto metrů, bylo by zhola nemožné ho sledovat.

Dříve než se do spojitosti zakousneme, řekneme si něco o limitách, které s ní velice úzce souvisí. Jde o poměrně náročnou disciplínu, proto nebudu příliš zacházet do technických detailů. Kdo vydrží až do finiše, může si v samotném závěru protáhnout mozkové závity větou o dvou policajtech. Ta nám umožňuje některé komplikovanější limity spočítat.

Slovo do pranice: Limita

Každá kultura má své rituály dospívání. Říká se, že z indiánského chlapce se stává kmenový bojovník, když skolí svého prvního jelena. S trochou nadsázky bychom mohli říci, že mladý počtář se stane platným matematikem, když spočítá svou první limitu. Limita je ten moment, kdy se do běžných kupeckých počtů vloudí přízrak nekonečna.

Hlavní roli v této pohádce bude hrát nekonečná posloupnost čísel. Tady je příklad (posloupnost reciprokých hodnot 1/n):

1/1, 1/2, 1/3, 1/4, 1/5, 1/6, 1/7, 1/8, 1/9, 1/10...

Když si tato čísla představíte, popřípadě vyčíslíte na kalkulačce, zjistíte, že mají jednu zajímavou vlastnost. Básník by řekl „stávají se menšími a ještě menšími až budou nejmenšími na celém světě". O něco techničtěji – jejich hodnoty se stále více přibližují k nule. Jak ale takovou skutečnost zachytit formálně?

Naivně bychom mohli říci, že poslední člen posloupnosti bude nula, jenže nekonečná posloupnost poslední člen nemá. A tak si matematici místo něj vymysleli limitu. Když si představíte, že podél posloupnosti jedete v tramvaji a zapisujete si její hodnoty, tak limita je číslo, které by se ve vašem zápisníčku objevilo, kdyby se vám podařilo dojet až na konečnou. Tedy vlastně nekonečnou.

Je to něco podobného, co jsme viděli u nekonečných řad. Jediný rozdíl je, že tam jsme při výletu podél řady její členy sčítali, zatímco tady pouze vyčíslujeme jejich hodnotu (což je většinou o dost jednodušší). Na součty nekonečných řad se můžeme dívat jako na speciální případ limit (matematici na to mají takové jedno kouzelné zaříkávadlo: „součet nekonečné řady je limita posloupnosti jejích částečných součtů“. To se vám bude jednou hodit, až budete na námluvách u své milé a při sváteční večeři budete mít z druhé strany strýčka podivína z Matematického ústavu Akademie věd).

Zkrátka limita je číslo, ke kterému se členové dané posloupnosti více a více přibližují. Technicky říkáme, že taková posloupnost k limitě konverguje (blíží se). Ovšem zdaleka ne každá posloupnost má svou limitu. Pokud se posloupnost k ničemu neblíží, tak prostě řekneme, že žádnou limitu nemá. Například následující posloupnost si jen tak nezávazně poskakuje a limitu má na háku.

0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1...

Ani další posloupnost limitu nemá, přestože by se na první pohled mohlo zdát, že bude mít limitu nula. Ale není tomu tak.

1.2, 1.1, 1.0, 0.9, 0.8, 0.7, 0.6, 0.5, 0.4, ...

Zatímco u první posloupnosti se čísla sice také zmenšovala, ale s menší a menší intenzitou (takže nakonec do té nuly krásně dosedla jako přistávající letadlo), zde nám hodnoty ubývají rovnoměrně a je jen otázkou času, kdy se dostanou pod nulu. Ani tam se však klesání nezastaví a hodnoty pokračují v pádu do záporných čísel (někdy v této situaci říkáme, že posloupnost má za limitu minus nekonečno).

Aby bylo jasné, že limita nemusí být nutně nula, tady je poslední příklad:

2/1, 5/4, 10/9, 17/16, 26/25, 37/36, ...

- tady bychom n-tý člen mohli zapsat vzorečkem jako x_n = (n²+1)/n²

Limitou této posloupnosti, tedy hodnotou, kterou byste nalezli na jejím „konci“, je 1.

Z uvedených příkladů je jasné, že by bylo dobré mít nějakou definici limity, abychom nemuseli hádat, zda ji daná posloupnost má a nebo nemá. A řekneme si ji nejprve pro posloupnost bodů, protože geometricky je to trochu názornější (koneckonců číslo není nic jiného než bod na číselné ose, takže jakmile pochopíte definici limity pro bod, můžete se na výše uvedené posloupnosti dívat jako na speciální případy).

Tak jedem.

Bod x je limitou posloupnosti bodů x₁, x₂, x₃, ..., pokud platí, že pro každé okolí bodu x (ať je jakkoli malinké) se celá posloupnost od jistého indexu do tohoto okolí vejde (tedy že se v něm bude celá nalézat).

Intuitivně je jasné, co chceme říci. Pokud konvergujete k soše koně na Václavském náměstí (tj. sv. Václav je limitou vaší trajektorie), tak je jasné, že od jistého okamžiku se vaše životní dráha (dívejme se na ni jako na posloupnost poloh) bude nalézat v katastru hlavního města Prahy (tedy v okolí „koně“). Důležitá jsou v této definici dvě slova. Za prvé: musí to platit pro každé okolí (jinak byste si to katastrem města Prahy mohli namířit třeba do Libně a definice limity by to nepoznala), to znamená, že i pro menší územní celky, jako je Praha 1 nebo dokonce okolí Václavského náměstí, musí platit, že od jistého okamžiku se vaše trajektorie bude nalézat uvnitř tohoto celku. A za druhé, posloupnost nemusí v okolí ležet celá - bohatě postačí, pokud v něm bude počínaje od jistého indexu dál. Jinými slovy, limitě je jedno, co jste dělali, než jste přijeli do Prahy. Můžete si klidně brouzdat Saharou, ale dříve nebo později se musíte začít stahovat ke koni. Technicky říkáme, že limita vyjadřuje asymptotické chování dané posloupnosti. Tedy to, co posloupnost dělá „v nekonečnu“, přesněji pro velké hodnoty indexu n. Co si posloupnost dělá v úvodu, to hodnotu limity (a její existenci) neohrozí.

Abyste si mohli udělat vlastní obrázek, tady je pár příkladů bodových posloupností:

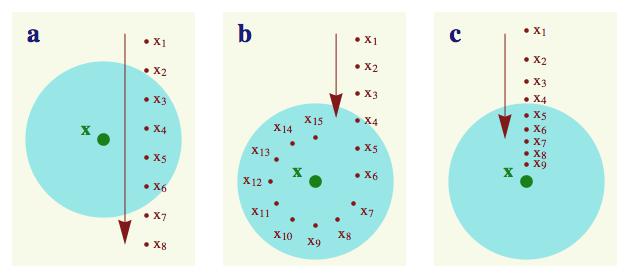
Posloupnost na obrázku a sice do vyznačeného okolí (světle zelené) vběhne, ale poměrně rychle z něho zase vyběhne, takže tato posloupnost k bodu x nekonverguje.

Posloupnost na obrázku b se od jistého indexu ve vyznačeném okolí skutečně udrží (představte si, že od bodu x₁₅ posloupnost dál obíhá kolem bodu x ve stejné vzdálenosti - jako jakási planeta), ale posloupnost přesto k x nekonverguje. Ona se sice zdržuje bodu x „na dohled“, ale nepřibližuje se k němu. Tady vidíme, proč je v definici nutno trvat na výrazu „pro každé okolí bodu x“. Když totiž poloměr světle zeleného kotoučku zredukujeme zhruba na třetinu, „kroužící posloupnost“ se najednou do okolí nevejde (a to ani „od jistého indexu“). Proto ani tato posloupnost bodů k x nekonverguje. Nemá limitu.

Teprve na obrázku c máme příklad posloupnosti, která k bodu x konverguje (bod x je její limitou). Samozřejmě si ji musíte představit jako nekonečnou, tedy za bodem x₉ následuje x₁₀, x₁₁, x₁₂ a tak dále. Vidíte sami, že i když kotouček podstatně zmenšíte, od jistého bodu se posloupnost do kotoučku stejně zase dostane a zůstane v něm. Ten „jistý bod“ už sice nebude x₅ (jako na obrázku), ale bude to třeba bod x₆₇, ale to nevadí. Počínaje tímto bodem se zbytek posloupnosti do okolí (kotoučku) už vejde. A přesně o to v definici limity jde.

Specializace na čísla je potom nabíledni. Číslo je bodem na číselné ose, jeho okolím je interval - tedy množina bodů, které se od daného čísla moc neliší - a dokazování existence limit se tím redukuje na žonglování s různými nerovnostmi. Toho vás ale ušetřím.

Upřímně řečeno, z čistě praktického hlediska vytušíte, zda daná posloupnost x_n má limitu a nebo ne, když si do ní dosadíte několik zvětšujících se hodnot n (např. n=10, 100, 1000 a 10000) a spočítáte si příslušné členy na kalkulačce. Většinou lehce zjistíte, zda se to k něčemu blíží či ne. Samozřejmě na technické škole by vás profesor za takový přístup vyrazil od zkoušky, ale v praxi to funguje docela dobře (protože příroda nám většinou - na rozdíl od pana profesora - nedává „špeky“).

Jako cvičení si můžete zkusit ověřit, že posloupnost n²/exp(n) konverguje k nule, zatímco posloupnost (n³ + n)/(n³ - 3) konverguje k jedničce. Technicky to zapíšeme takto:

lim n²/exp(n) = 0

lim (n³ + n)/(n³ - 3) = 1

s tím, že pod znakem limity někdy najdete malý symbol: n šipka nekonečno (což čteme limita posloupnosti ... pro n blížící se k nekonečnu).

Spojité funkce

Minule jsme si řekli, že funkce je spojitá, pokud malé změně na vstupu (x) odpovídá malá změna na výstupu (y). To je ale trochu vágní, protože některé funkce se mohou změnit velmi rychle, aniž by ztratily spojitost. Ne vždy máme po ruce obrázek a zadání pouze dvou nebo tří hodnot může být matoucí. Vezměme si třeba následující funkci, jejíž hodnotu jsme si vyčíslili v bodě x. Pak jsme si poměrně blízko vybrali testovací bod X a také zde spočítali funkční hodnotu (to jsou ty zelené úsečky). Přestože se vstupní hodnoty x a X moc neliší, hodnoty na výstupu, tedy f(x) a f(X), se změnily velmi podstatně. Kdybychom neměli obrázek, klidně bychom mohli naši funkci podezřívat z nespojitosti.

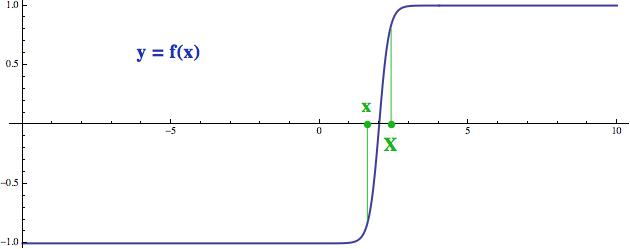
Na zjištění případné nespojitosti nám nestačí vzít si jen dva body. To je příliš hrubý mechanismus. Potřebovali bychom si okolí bodu x, ve kterém tušíme nespojitost, „osahat“ bližšími a bližšími testovacími hodnotami. A takovou „rukou šátralkou“, která nám umožní si okolí bodu x prozkoumat v libovolném rozlišení, je právě limita. Jejím prostřednictvím můžeme do inkriminovaného okolí vyslat posloupnost testovacích vstupních bodů pomalu se blížících k hodnotě x a přitom sledovat chování příslušných funkčních hodnot.

Podívejme se nejdřív, jak by to vypadalo v případě spojité funkce.

Vezmeme si nějaký bod x (ve kterém zjišťujeme spojitost), necháme k němu dokonvergovat nějakou posloupnost x₁, x₂, x₃, x₄, ... (na obrázku jsem pochopitelně znázornil pouze první tři) a spočítáme si funkční hodnoty v těchto bodech. Ty si označíme y₁, y₂, y₃, y₄... Funkční hodnotu v bodě x si označíme jako obvykle písmenkem y, tedy y = f(x). Na obrázku dole si všimněte, že jak se posloupnost x_n hezky přibližuje hodnotě x, posloupnost y_n se stejně hezky přibližuje hodnotě y. A to platí, ať si tu posloupnost x_n vybereme jakkoliv!

Podívejme se teď na mechaniku této funkce prostřednictvím trpaslíka v krabičce z minulého Matykání. Postavíme se ke vstupu a k výstupu pošleme kamaráda Frantu, aby nám hlásil, co se bude dít. Pak začneme do vstupu házet naše konvergující čísílka x_n a zeptáme se Franty, zda to, co vidí na výstupu, taky konverguje (tedy blíží se nějaké hodnotě). Franta po chvíli zahlásí, že jeho ypsilonka skutečně k čemusi konvergují. A tady nás napadne, že když všechna jeho ypsilonka jsou beztak jen výstupem toho, co jsme tam z naší strany naházeli, tak třeba ta Frantova tajemná limita bude prostě taky jen výstupem, pokud trpaslíkovi nabídneme tu naši limitu. Vezmeme tedy bodík x, hodíme ho do funkce a Franta vzápětí radostně hlásí: "No, čoveče, to co mi tady vylezlo na výstupu (tedy y), je přesně to, k čemu ta moje posloupnost konverguje!"

A to je přesně to, co charakterizuje spojitost.

Funkce f je spojitá v bodě x, pokud pro každou posloupnost bodů x₁, x₂, ... konvergujících k x, posloupnost příslušných funkčních hodnot (y₁, y₂, ...) konverguje k f(x), což jsme si výše označili písmenkem y.

Vidíme tedy, že spojité funkce v jistém smyslu „respektují“ limity. Mám pro vás další kouzelné zaříkávadlo, až budete sedět vedle podivínského strýčka: „funkční hodnota v limitě je limita funkčních hodnot“. Ten bude panečku koukat, co z vás leze za moudra.

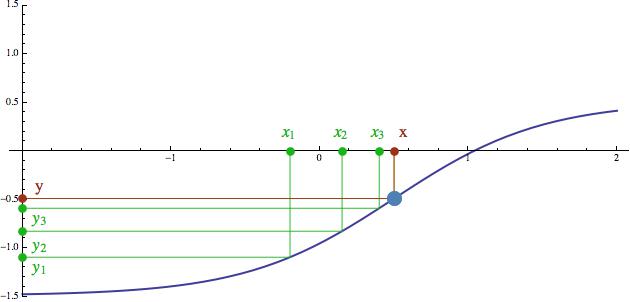
Podívejme se teď, co se stane, když funkce spojitost ztratí. Vezmeme si tu předchozí a v bodě x jí trochu „natrhneme sako“.

Vidíme, že i tady nám funkční hodnoty (tedy body y₁, y₂, y₃, ...) k něčemu konvergují, ale to, k čemu konvergují, už není f(x). Je to nějaké úplně jiné číslo, které jsem na obrázku dole označil jako L. Na ose y tedy máme k dispozici dvě různé hodnoty. Jednak L, ke kterému konvergují výstupy (funkční hodnoty), a jednak y, což je funkční hodnota v bodě, ke kterému konvergovaly vstupy. Nespojité funkce tedy limity „nerespektují“.

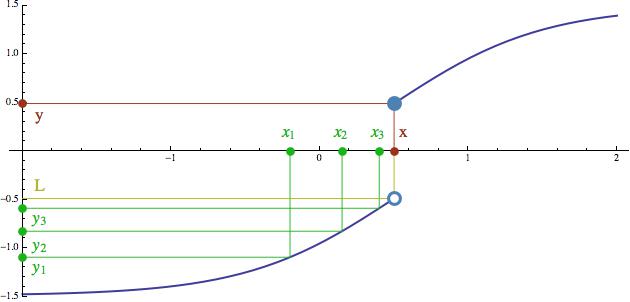
(prázdné kolečko indikuje, že v bodě x už máme používat tu horní větev)

Pokud trpaslíkovi naházíte na vstup posloupnost konvergujících x-ových hodnot, tak hodnoty na výstupu nespojité funkce buď nebudou konvergovat vůbec, a nebo budou konvergovat k něčemu jinému než k y. Franta bude zklamán.

Teď si určitě říkáte, k čemu je takováto šílenost dobrá. V první řadě je dobrá k tomu, aby byl veledůležitý pojem spojitosti postaven na solidní rigorózní základ. Tedy abychom dokázali přesně říci, které funkce jsou spojité a které ne, a v jakých bodech. Ale také nám umožňuje některé funkce dodefinovat v bodech, ve kterých se originální definice nedá použít, ale ke kterým se dá „dokonvergovat“ pomocí vhodně zvolené posloupnosti. To znamená, že pokud pro nějaké zatrolené x nejsme schopni zjistit hodnotu f(x), můžeme ji nahradit hodnotou L a odůvodnit to tvrzením, že se snažíme vytvořit funkci, která je spojitá. To vám každý soudce sežere, protože nespojité funkce nemá nikdo rád. Minule jsme například viděli Minkowského funkci, která se dá sice krásně definovat pro racionální čísla, ale pro iracionální ne. Na předposledním obrázku si představte, že červená hodnota x je nějaké iracionální číslo. Hodnota funkce v bodě x se z definice zjistit nedá. Musíme si tedy nabrnkat posloupnost racionálních bodů, která k x konverguje (to jsou ty zelené bodíky na ose x), pak se podíváme, k čemu nám konvergují jejich obrazy (zelené bodíky na ose y) a tuto hodnotu prohlásíme za funkční hodnotu v bodě x, tedy f(x) neboli přímo y. Chceme totiž, aby funkce, kterou konstruujeme, byla spojitá. Pokud bychom na spojitosti netrvali, mohli bychom si samozřejmě hodnotu Minkowského funkce v iracionálních bodech vymyslet zcela libovolně, ale taková funkce by pak byla k ničemu. A to nás pomalu přivádí k hlavnímu tématu dne. K policejnímu sboru.

Funkce sin(x)/x je krásná funkce (graf uvidíte za chvilku), která je definovaná všude s výjimkou počátku (x=0). Tam bychom museli dělit nulou a to se v matematice neodpouští. Ukazuje se však, že s pomocí limity si funkci můžeme v počátku krásně dodefinovat a učinit z ní občansky spořádanou a všude spojitou funkci. Musíme ale najít nějakou posloupnost, která konverguje k nule (to bude naše „ruka šátralka“), a s její pomocí pak zjistíme, jak se funkce v okolí nuly chová, a tedy jaká hodnota v nule by se jí tak asi „šikla“. K tomuto účelu budeme potřebovat jednu technickou větu o limitách.

Sekce jauvajs: Věta o dvou policajtech

(jen pro otrlé jedince)

Obrazný smysl této věty je jednoduchý. Pokud dva policajti vedou zločince mezi sebou a oba mají namířeno do stejného místa (řekněme k policejní stanici), pak zmíněnému zlosynovi nezbyde, než se odebrat tamtéž. Těžko byste mohli kráčet k hlavnímu nádraží, když vás za každý loket drží jeden policajt a oba mají namířeno na policejní stanici. Technicky řečeno - pokud oba policajti konvergují k bodu A, milému zloději nezbyde než konvergovat tamtéž.

S limitami je to podobné. Budeme uvažovat tři posloupnosti, a to tak že posloupnost, která nás zajímá (budu jí říkat b), bude vždy vklíněna mezi dvě postranní posloupnosti a a c. Přesně tak, jako je zločinec vklíněn mezi dva policisty. Věta o dvou policajtech pak říká, že pokud dvě postranní posloupnosti konvergují ke stejné limitě (tj. policajti mají namířeno do stejného místa), pak posloupnost b musí mít nutně tu samou limitu (zločinec musí volky nevolky konvergovat tam, co policisté).

Abych trochu zpřesnil tu „vklíněnost“, každý člen posloupnosti b bude menší než příslušný člen posloupnosti c a větší než příslušný člen posloupnosti a. Pokud si členy označíme jako a_n, b_n a c_n, budou od jistého indexu platit tyto nerovnosti:

a_n < b_n < c_n

A teď už se podívejme na funkci sin(x)/x v nule.

Na ose x si vybereme posloupnost x_n = 1/n, která k nule konverguje, a budeme se snažit zjistit, k čemu konvergují příslušné funkční hodnoty y_n. Budeme tedy počítat limitu sin(1/n)/(1/n).

Limitu si můžete zkusit sami najít na kalkulačce. Já vám ji ale dokážu pomocí věty o dvou policajtech. Nejdříve si musíme připravit nějaké ty nerovnosti a to uděláme z geometrie. Představme si kruhovou výseč s jednotkovým poloměrem a dva trojúhelníky, tak jak to vidíme na obrázku. Úhel výseče si označíme písmenkem x. Naznačená výška trojúhelníku ABC pak bude sin(x) a strana BD se bude rovnat tan(x). To je čistě středoškolská geometrie (délka strany AC je taky jedna - poloměr kružnice).

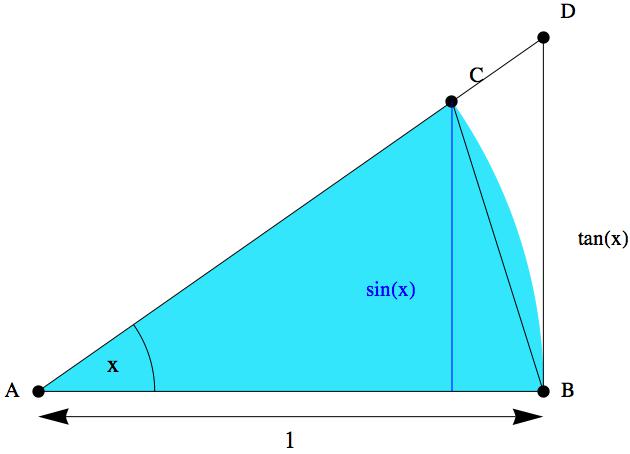
Z obrázku je vidět, že obsah naznačené kruhové výseče je menší než obsah trojúhelníku ABD, ale větší než obsah trojúhelníku ABC. Máme tedy schematicky:

obsah (ABC) < obsah (výseč) < obsah (ABD)

No a už se nám tam ty dva policajti po stranách rýsují. Budeme to ale muset všechno vyčíslit pomocí proměnné x a trochu algebraicky pofackovat. Obsah výseče jednotkového kruhu (jejíž úhel v radiánech je x) se rovná x/2. Obsahy trojúhelníků dostaneme z klasického „základna (ta je rovna 1) krát výška děleno dvěma“. Takže máme:

sin(x)/2 < x/2 < tan(x)/2

a po vynásobení 2 dostaneme:

sin(x) < x < tan(x)

Teď obě strany vydělíme hodnotou sin(x) a vezmeme převrácené hodnoty (čímž se nám obrátí smysl všech nerovností - rozmyslete si to: pokud je x < y pak platí 1/x > 1/y). Pokud je úhel x v prvním kvadrantu, sinus i kosinus jsou kladné, takže nám vyjde:

cos(x) < sin(x)/x < 1

(pokud se vám to s tou převrácenou hodnotou nezdá, můžete si alternativně analyzovat obě nerovnosti odděleně pomocí algebraických úprav a dostanete to samé)

A teď si vezmeme speciální hodnotu x = 1/n a dostaneme se konečně k posloupnostem:

cos(1/n) < sin(1/n) / (1/n) < 1

Máme kýžené posloupnosti s tím, že zločinec je uprostřed a policajti po obou stranách. Napravo je konstantní posloupnost 1, takže ta má limitu 1. Nalevo je spojitá funkce kosinus, uvnitř máme posloupnost, která konverguje k nule, takže funkční hodnoty budou konvergovat k hodnotě cos(0), což je taky 1. Takže zločinec uprostřed nemá jiného zbytí než také konvergovat k 1.

Quod erat demonstrandum.

Posloupnost sin(1/n) / (1/n) tedy konverguje k 1.

Co jsme to ukázali? Vzali jsme si funkci, která nebyla v nule definovaná. Nedala se v ní vyčíslit. Proto jsme si vzali posloupnost 1/n, která k nule konverguje, a ukázali jsme, že jak se potichoučku polehoučku blížíme nule, posloupnost příslušných funkčních hodnot (to je ta poslední věta předchozího odstavce) konverguje k 1. Je tedy přirozené dodefinovat tuto funkci v nule jedničkou. Instruujeme tedy trpaslíka, že pokud mu někdo na vstup hodí 0, tak ať nepanikaří a prostě na výstup vyhodí 1. Tím jsme mazaně obešli skutečnost, že nulou se dělit nesmí a tímto postupem dostali krásnou spojitou funkci s následujícím grafem.

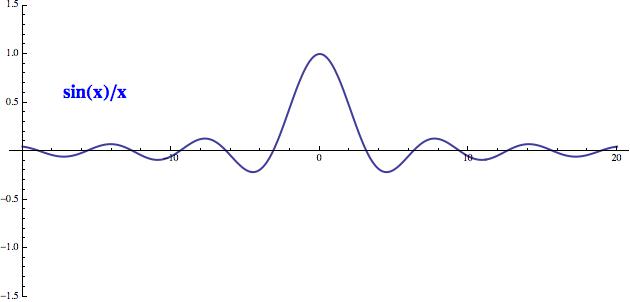
Všimněte si, že v nule není ani stopa po nějakém problému. A to všechno jsme zvládli díky větě o dvou policajtech. Česká policie by si věru mohla do štítu vepsat heslo: „Chránit a pomáhat s počítáním limit“.

Článek je redakčně upravenou verzí blogového příspěvku na serveru iDNES.cz. Publikováno s laskavým svolením autora.

Další díly a původní texty jsou dostupné na blogu Jana Řeháčka.

Autor: Jan Řeháček