Napadlo vás někdy, proč není celá noční obloha ozářená, když je ve vesmíru nekonečně mnoho hvězd? Pokud ano, tak nejste sami. Podobnou myšlenkou se už v roce 1823 zabýval německý astronom Heinrich Olbers.
Nebojte se, nemám v úmyslu fušovat do řemesla astronomům a fyzikům. Jen si dnes ukážeme, jak si v naší vlastní hlavě můžeme pomocí racionálních čísel vytvořit projektivní model vesmíru, který nám umožní, abychom o tomto paradoxu mohli přemýšlet takříkajíc na vlastní pěst. A tyto úvahy nám na oplátku poskytnou zajímavou vizualizaci racionálních čísel.
Olbersův paradox spočívá zhruba v této úvaze: Pokud je vesmír nekonečný a obsahuje nekonečně mnoho náhodně rozložených hvězd, tak by se každá linie pohledu, vedená z našeho oka, měla po čase s nějakou hvězdou protnout, a celá noční obloha by tudíž měla svítit.
Samozřejmě, abychom se s problémem mohli opravdu popasovat, museli bychom vzít v úvahu celou řadu faktorů, které leží mimo zónu matematiky – např. rozložení a svítivost hvězd anebo optické a geometrické vlastnosti mezilehlého prostoru. Jak to s Olbersovým paradoxem ve skutečnosti je, proto přenechám povolanějším.
Dnes se vás jen pokusím přesvědčit, že nekonečný počet hvězd nemusí nutně znamenat, že každý pohled, který směrem do vesmíru vrhneme, musí dříve nebo později protnout povrch nějaké hvězdy. Nejprve si však musíme vytvořit co nejkonkrétnější představu racionálních čísel, na kterých bude začátek této myšlenkové expedice založen.
Racionální čísla
Na obrázku níže jsem zaznamenal všechna racionální čísla na intervalu (0, 1) s tím, že levý okraj odpovídá nule a pravý jedničce. Na n-tou linku vynesu zlomky v základním tvaru, jejichž jmenovatel je přesně n. Řádek nula můžeme přeskočit, protože nulou se ve slušné společnosti nedělí. Na řádku jedna vidíme dva body odpovídající zlomkům 0/1 a 1/1. Na řádku dvě máme uprostřed zlomek 1/2 a na řádku tři sedí zlomky 1/3 a 2/3 - přesně tam, kde by měly podle zákonitostí číselné osy sedět. Na řádku čtyři vidíme pouze 1/4 a 3/4 (2/4 jsem vynechal, protože nejsou v základním tvaru – už je máme zachycené výše jako 1/2). Jinými slovy, řádky odpovídající prvočíselným jmenovatelům v sobě nesou všechny možné bodíky (to jsou ty plné řádky), zatímco u řádků, které odpovídají složeným jmenovatelům, jsou některé body vynechané (tam, kde by čitatel byl soudělný se jmenovatelem – např. na dvanáctém řádku přeskakuji zlomky: 2/12, 3/12, 4/12, 6/12, 8/12, 9/12 a 10/12). A tento obrázek pochopitelně pokračuje dál směrem „dolů“ – zlomky se jmenovatelem 101, 102 a tak dále.
A teď si představte, že všechny barevné kotoučky jsou skutečně jen malilinkaté bezrozměrné bodíky a že všechny popadají jako zralé hrušky na zem. I z těch řádků „dole“, které na obrázku nevidíte. To, co pak na zemi najdete, jsou přesně racionální čísla (mezi 0 a 1). A jako taková mají dvě důležité vlastnosti. Za prvé je jich nekonečně mnoho, což je vidět například z toho, že už jen čísel tvaru 1/2, 1/3, 1/4, ... (to je ta levá okrajová větev) je nekonečně mnoho. A za druhé jsou na intervalu (0, 1) rozložené zcela hustě. Tedy nenajdete na něm žádný kousek „země“, na kterém by žádné zlomky nebyly. Přesněji, každý otevřený interval, byť by byl sebemenší, nějaké to racionální číslo obsahuje. Přitom však nezapomeňte, že kompletně jimi „zem“ pokryta není. Většina čísel je stále iracionální.
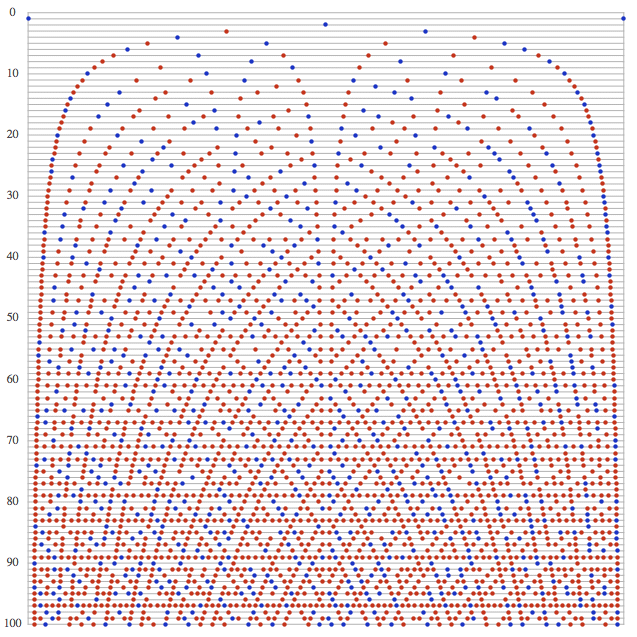 (bodíky jsem rozlišil na modré a červené především proto,
aby nebyl obrázek tak fádní, ale koho to zajímá, tak modré body
odpovídají zlomkům M/N, pro které je komplexní číslo M+iN gaussovské
prvočíslo – pro naše dnešní potřeby je to však irelevantní)
(bodíky jsem rozlišil na modré a červené především proto,
aby nebyl obrázek tak fádní, ale koho to zajímá, tak modré body
odpovídají zlomkům M/N, pro které je komplexní číslo M+iN gaussovské
prvočíslo – pro naše dnešní potřeby je to však irelevantní)
Než postoupíme dál, rád bych poznamenal, že hustota racionálních čísel na jednotkovém intervalu trochu připomíná rozložení hvězd na noční obloze. Když básník mluví o „nebi posetém hvězdami“, odvolává se v podstatě na podobný pojem hustoty, který používají matematici. Tedy v každém kousku oblohy (můžete si ho představit jako pomyslný kotouček měsíce) nějakou hvězdu najdeme. Zda je v případě hvězd tato poetická představa správná, je otázka pro astronomy.
My si teď sestrojíme jednoduchý model vesmíru a začneme šťourat do Olbersova paradoxu.
Model A
Jako základ si vezmeme jednotkový interval (0, 1), který představuje svislá černá čára dole, a pomocí zelených bodíků si na něm vyznačíme racionální čísla (aby byly vidět, tak jsem je musel nakreslit jako puntíky, ale i nadále si je budeme představovat jako malilinké bezrozměrné body). Na obrázku je jich samozřejmě jen konečně mnoho, ty ostatní si musíte vybájit ve vlastní fantazii. Z fialového bodu vlevo budeme náš pomalu vznikající vesmír pozorovat.
V první řadě každým zlomkem (zeleným bodem) proložíme přímku, která prochází naším stanovištěm (fialový bod). Protože přímka je určena dvěma různými body, není to konstrukčně nic těžkého. Na „druhé“ straně černé úsečky si podél těchto přímek rozložíme hvězdy, takže na zelené body (racionální čísla) se můžeme dívat jako na projekce červených hvězd na černý strop planetária. Jak daleko hvězdy posadíte, je v podstatě jedno (ale protože každá hvězda odpovídá racionálnímu číslu M/N, můžete si je – čistě pro určitost – představit třeba ve vzdálenosti M + N od černé úsečky.
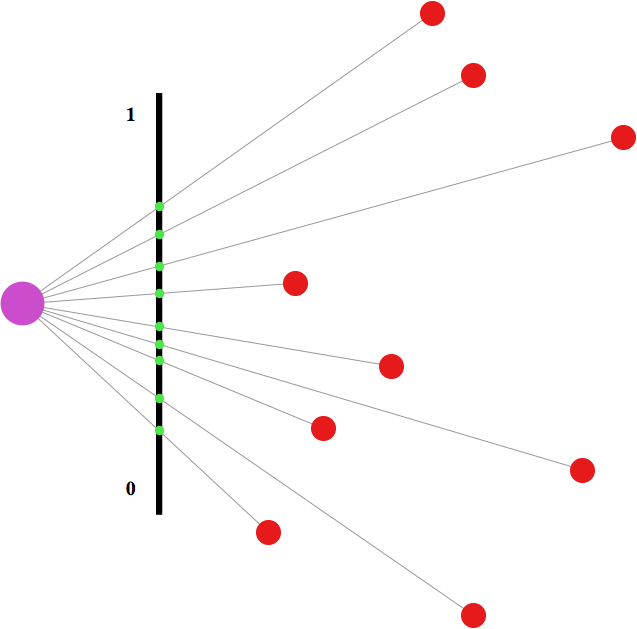
Pokud se teď posadíme do fialového bodu a pohlédneme na noční oblohu
hvězdárny (černá svislá čára), uvidíme dva typy bodů. Zelené, které
odpovídají racionálním číslům a budou „svítit“, protože za nimi
leží hvězda, a ty ostatní, které svítit nebudou.
Ostatních bodů (odpovídajících iracionálním číslům) je také nekonečně mnoho. Dokonce jsme v jednom minulém Matykání viděli, že je jich nespočetně mnoho. Tedy v jistém smyslu je jich většina. Tohle je první náznak, že to s tím úplným osvětlením oblohy možná nebude tak horké. Tady totiž máme jednoduchý model vesmíru s nekonečně mnoha hvězdami, a přesto bude strop planetária většinou tmavý (složený z černých iracionálních bodíků).
Tato úvaha má však jeden velký háček. Předpokládáme, že zelené bodíky (obrazy hvězd) jsou zcela bezrozměrné, že jsou to opravdu jen geometrické body. To však ve skutečnosti není pravda. Hvězdy za nimi mají jistě nenulový rozměr, a zelené průměty na strop planetária budou mít tudíž nějaký nenulový poloměr. Nebudou to body v pravém smyslu slova, ale malilinkaté kotoučky. Jejich poloměr bude neskutečně malý, ale nebude to nula (jako je tomu u bodů). O něco přesněji: hvězdy budou mít při pohledu z fialového stanoviště nějakou nenulovou úhlovou velikost (viz níže sekce Jauvajs). A v okamžiku, kdy zelené bodíky „přifoukneme“ na správnou velikost, tak nám třeba černé skvrny tvořené iracionálními čísly úplně vymizí (představte si dva zelené balonky, které se nedotýkají – trochu je přifouknete, balonky se najednou dotknou a černý prostor mezi nimi je fuč).
Naštěstí se ukáže, že když přifukování zelených bodíků budeme provádět opatrně, nějaký ten černý prostor mezi hvězdami nám pořád zbyde. Dokonce si v našem vylepšeném modelu budeme moci přesně určit, kolik nám ho zbyde. Za tím účelem si zcela libovolně vybereme nějaké hodně malé číslo a označíme si ho m. Pokud nemáte rádi proměnné, klidně si ho představujte jako nějaké konkrétní malé číslo – třeba 0,001.
Protože v tomto modelu hvězdy odpovídají racionálním číslům, můžeme si je očíslovat přirozenými čísly, tedy od jedné do nekonečna (odvoláváme se na to, že racionální čísla jsou spočetná, pro iracionální čísla by nám očíslování neprošlo). A teď když máme naše malé číslo m zvolené a hvězdičky hezky očíslované, můžeme začít s konstrukcí modelu.
První hvězdě na našem seznamu přisoudíme takový poloměr, že její (zelený) průmět na černý jednotkový interval bude mít velikost (přesněji délku) přesně m/2. U druhé hvězdy to zaonačíme tak, že její průmět na strop hvězdárny bude m/4, u třetí m/8, u čtvrté m/16 a tak dále. Ve jmenovateli tedy protáčíme mocniny dvojky. Hvězdy stále sedí tam, kam jsme je posadili, jenom jsme teď z jejich bodových obrazů udělali realističtější malé kotoučky s výše uvedenými velikostmi.
Z matematického pohledu jsme všechna racionální čísla (zelené tečky) „obalili“ malým intervalem, aby získala určitou velikost, která se dá změřit (a posléze i posčítat). A výpočet není nijak komplikovaný. Naše planetárium (jednotková úsečka) má délku jedna. Když sečteme velikosti všech zelených hvězdiček (tedy přesněji jejich průmětů na strop hvězdárny), tak dostaneme nekonečnou řadu m/2 + m/4 + m/8 + m/16 + m/32 + ... Z tohoto výrazu vytkneme m a dostaneme: m krát (1/2 + 1/4 + 1/8 +...). A protože nekonečná geometrická řada v závorce má součet roven 1, je celkový součet délek všech zelených úseček roven m.
V zásadě to znamená, že z celkové délky 1 bude svítit pouze část oblohy o celkové délce m. Pokud jste si číslo m představili jako 0,001, tak zbytek „oblohy“ o celkové délce 0,999 bude tmavý. Jinými slovy, budete-li se dívat z onoho fialového bodu na oblohu, v 0.1 % případů se paprsek vycházející z vašeho oka protne s nějakou hvězdou a v 99.9 % případů se s žádnou hvězdou neprotne.
Pro rejpaly poznamenávám, že součet m je de facto horním odhadem, protože průměty některých hvězd se mohou částečně překrývat. Takže svítící (zelená) část oblohy bude ve skutečnosti o něco menší.
Nastavením konstanty m si můžeme vytvořit model vesmíru, který bude zářit jako blázen (pokud je m nějaké velké číslo), ale také takový, kde bude obloha většinou temná – pokud bude číslo m velice malé (čím je m menší, tím větší část oblohy bude v našem modelu temná).
A ještě jeden technický detail. Z pohledu racionálních čísel jsme právě ukázali jednu zajímavou věc. Celá tato množina se dá pokrýt malými intervaly, jejichž souhrnná délka je m. A ta se tím pádem dá udělat libovolně malá. O množinách, které splňují tuto vlastnost, říkáme, že mají míru 0 (slovo „míra" si představte jako zobecnění slova „délka"). My jsme to sice ukázali pouze pro racionální čísla na intervalu (0,1), ale pro všechna racionální čísla se to ukáže obdobně.
Model B
Teď si vytvoříme o něco realističtější model v tom smyslu, že hvězdy budou rozhozeny po celém (dvourozměrném) prostoru. I ve třech dimenzích by to šlo, ale už by se to obtížně kreslilo. Stropem našeho planetária, ve kterém budeme hvězdy pozorovat, tentokrát nebude úsečka, ale jednotková kružnice. Jinak je princip konstrukce podobný a žádný nový trik v tomto oddílu nenajdete.
V modelu A jsme umístili zelené průměty hvězd do racionálních čísel a hvězdy jsme pak posadili na paprsky (čili polopřímky) těmito body procházejícími. V tomto modelu budeme postupovat obráceně. Nejprve si do dvourozměrného prostoru náhodně posadíme červené hvězdy (viz obrázek níže), pak si je promítneme na černou kružnici planetária a nakonec jim přisoudíme poloměry tak, aby se jejich zelené průměty opět daly sečíst geometrickou řadou.
Červených hvězd bude opět spočetné nekonečno a my si je tedy hezky očíslujeme (třeba podle vzdálenosti, takže nejbližší hvězda bude č. 1, ta další č. 2 atd.). Aby to bylo realističtější, tak na následujícím obrázku jsem zelené průměty nakreslil tak, že svou velikostí jakž takž odpovídají velikostem i vzdálenostem hvězd, které reprezentují (takže hvězdy menší nebo vzdálenější mají menší průměty). A otázka opět zní, zda lze vytvořit model vesmíru s nekonečnem hvězd, ve kterém zelené průměty nevyplní kompletně černou kružnici našeho pomyslného planetária.
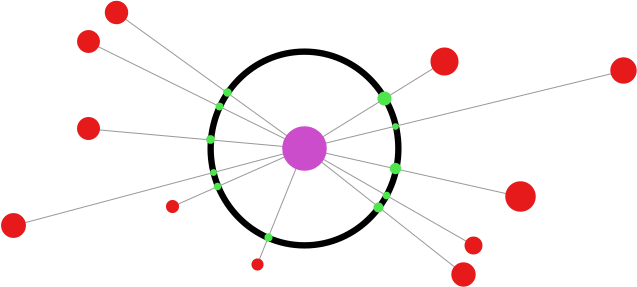
Výpočet proběhne stejně jako u modelu A s pomocí předem zvolené konstanty
m (např. 0,05). Takže první hvězdě přisoudíme takový
poloměr, aby její průmět do jednotkové kružnice byl přesně
m/2, druhá bude mít průmět m/4 a tak
dále. Průměty budu poměřovat úhlovou velikostí, takže si je můžete
představit ve stupních (nebo radiánech).
No a teď se postavíme do fialového bodu a opět si sečteme úhlový rozměr všech našich hvězd (respektive jejich obrazů na stropu planetária). Po vytknutí m dostaneme úplně stejnou geometrickou řadu, takže součet všech „zelených“ hvězdných obrazů bude opět m. A zbytek (tedy 360-m, pokud to měříme ve stupních) bude připadat na černočernou oblohu. Zase tedy vidíme, že i při náhodném rozložení hvězd si můžeme lehce zkonstruovat model vesmíru, ve kterém se paprsek z našeho oka (přímá linie viditelnosti) protne s nějakou hvězdou pouze v menšině případů. Jak malá menšina je, to opět záleží na tom, jak malé m jsme si zvolili.
Šťouralové by samozřejmě mohli namítnout, že model „tmavého“ vesmíru bychom si mohli vytvořit daleko jednodušeji tak, že by červené hvězdy stály za sebou jako vojáci v řadě. Bylo by jich potom také nekonečno, ale byly by všechny – z našeho pohledu – schované za první hvězdou a zbytek vesmíru by byl tmavý. To je sice pravda, já však budu předpokládat, že Bůh, který to všechno stvořil, není žádný škodolibý šprýmař, a že hvězdy po vesmíru rozházel víceméně náhodně.
Na závěr bych ještě rád zdůraznil, že jde pouze o model. Jeho smyslem bylo vyvrátit mylnou domněnku, že nekonečno hvězd na obloze musí nutně znamenat, že když se zadíváme do nějakého směru, tak se paprsek vyslaný z našeho oka musí vždycky protknout s nějakou hvězdou. Nemusí. Ale za určitých podmínek by samozřejmě mohl. Stejně tak bychom si totiž mohli sestrojit model vesmíru (s velkou hodnotou m), ve kterém by byly obrazy hvězd tak velké, že jejich součet by nám dal plný úhel a každý paprsek z oka by si pak nějakou hvězdu našel. Která z obou možností je ta pravá, to už je otázka pro astronomy. Na to je matematika krátká. Pro její zodpovězení bychom museli znát přesnou distribuci hvězd v pozorovaném vesmíru, jejich galaktickou strukturu atd.
Sekce jauvajs: Úhlová velikost
Aby to dnešní Matykání nebylo zase tak úplně abstraktní, podíváme se v závěru na skutečné úhlové rozměry některých nebeských těles. Představme si třeba Měsíc. Vezmeme si flintu a zamíříme na jeho „dolní“ okraj. Pak flintu maličko „přizdvihneme“ a namíříme na jeho „horní“ okraj. Úhel, o který jsme flintu museli pozvednout, se nazývá „úhlová velikost“ (v tomto případě Měsíce).
Nejprve však pár slov k měření úhlů. Úhly měříme nejčastěji ve stupních a nebo v radiánech. Plný úhel je 360 stupňů, každý stupeň má 60 úhlových minut (značeno 60') a každá minuta má 60 úhlových vteřin (60''). Objekty na obloze jsou tak malé, že se jejich úhlové rozměry většinou udávají v úhlových vteřinách. Někdy používáme pro měření úhlů radiány, které v podstatě vyjadřují velikost odpovídajícího kruhového oblouku na jednotkové kružnici. Na obrázku níže odpovídá úhlu u světlemodrý oblouček vlevo nahoře. Pokud si úhel změříte v radiánech, dostanete stejné číslo, jako když si spočítáte délku modrého obloučku (za předpokladu, že kružnice má poloměr jedna).
Takže plný úhel bude mít 2 pí radiánů a převod mezi těmito jednotkami si provedete trojčlenkou: je-li plný úhel 360 stupňů zhruba roven 6,28 radiánů, kolik je potom 55 stupňů? (6,28 * 55/360 = 0,96 radiánů). Důvod, proč matematika obecně preferuje radiány, spočívá v definici goniometrických funkcí. Kdyby se v nich používaly stupně, tak by se spousta užitečných vzorečků zaplevelila různými přepočítávacími koeficienty.
Obecně platí, že pokud počítáte jenom s úhly a nepatláte se moc v trigonometrii, tak můžete použít stupně, které jsou netechnicky založeným lidem srozumitelnější. Jenom je třeba dávat pozor na to, zda jsou úhly vyjádřeny jako desetinné stupně, a nebo pomocí stupňů-minut-vteřin. Např. 24,5 stupně se dá také zapsat jako 24 stupňů a 30 minut. Ovšem pokud se odvoláváte na nějaké vztahy z vyšší matematiky (např. pro malé úhly platí přibližná rovnice tg(x)~x), pak musíte použít radiány (tady už porovnáváte úhly s něčím jiným – zde konkrétně s poměrem stran v trojúhelníku).
Tak a teď zpátky na hvězdnou oblohu.
Úhlová velikost nebeského tělesa je veličina, která v sobě zahrnuje jak jeho skutečnou velikost (tedy poloměr r), tak jeho vzdálenost od nás (zde označenou jako d). Je to, zhruba řečeno, úhel sevřený přímkami procházejícími „koncovými“ (extrémními) body pozorovaného tělesa. Samozřejmě úhlová velikost červené hvězdy a jejího zeleného průmětu je stejná. Z toho důvodu se nám na obloze jeví Slunce a Měsíc jako zhruba stejně velké objekty, přestože Slunce je daleko větší (je však také příslušně více vzdálené).
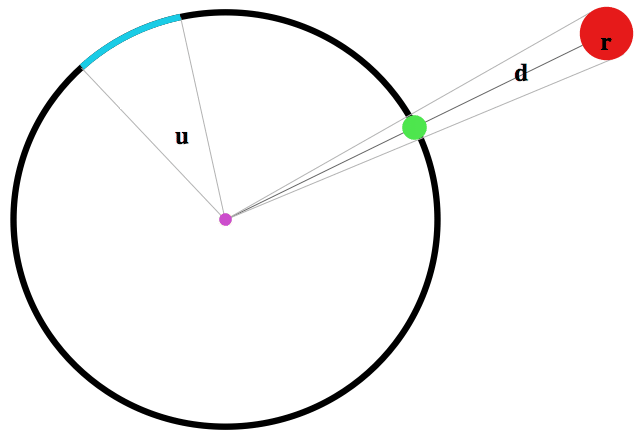
A teď konkrétní výpočet. Vzoreček pro úhlovou velikost u
je následující:
u = 2 arctg(r/d)
kde r je poloměr tělesa a d jeho vzdálenost. To se pro malé úhly dá ještě aproximovat pomocí výrazu u ~ 2 r/d (což je vlastně průměr vydělený vzdáleností). Jako příklad si vezmeme Jupiter. Když je Zemi nejblíže, nalézá se od nás 585 milionů km daleko. Jeho průměr je cca 70 tisíc km. Budeme-li vše počítat v tisících km (poloměr i vzdálenost musíme dosadit ve stejných jednotkách!), dostaneme:
u = 2 arctg(70/585000) = 0,000239316
(všimněte si, že to samé číslo dostanete i pomocí jednoduššího vzorečku)
Je to však v radiánech (použili jsme vyšší matematiku). Ve stupních by to bylo 0,0137118 (trojčlenku si sestavte za domácí úkol – dostanete u x 360 / 6,28). Pokud to chcete v minutách, vynásobte si stupňový výsledek 60: 0,8227', a pokud to chcete v úhlových vteřinách, tak ještě jednou vynásobit 60: 49,36''. Takže Jupiter se nám na obloze jeví jako kotouček s úhlovou velikostí cca 50 vteřin (když je nám nejblíž).
A co Mars? Myslíte, že se nám jeví větší nebo menší (když je nám nejblíž)?
Tak si to spočítáme. Mars se k naší planetě dokáže přiblížit na vzdálenost 56 milionů km a má poloměr 3,38 tisíc km. Takže to naházíme do vzorečku a vypadne nám cca 24,9 vteřin. Mars se nám tedy jeví zhruba jako poloviční ve srovnání s Jupiterem (ve smyslu úhlové velikosti).
A jak je to s tou zdánlivou „stejností“ Slunce a Měsíce? Slunce je od nás vzdálené 149,6 milionů km a jeho poloměr je 695,7 tisíc km. To nám dá úhlovou velikost zhruba 1 918 úhlových vteřin (to je o něco málo víc než půl stupně). Měsíc je od nás v průměru vzdálen 384 tisíc km a jeho poloměr je 1,737 tisíc km. To odpovídá úhlové velikosti 1 866 vteřin. Je tedy zdánlivě o fous menší (ale ona ta jeho vzdálenost dost kolísá, takže pokud se dostatečně přiblíží, může být i o fous větší než Slunce).
Na závěr si dáme nějakou opravdovou hvězdu, třeba Sirius. Ten je od nás vzdálen 8,6 světelných let (přepočítejte si to před dosazením na km) a má poloměr 1,19 milionů km. Pokud to všechno naházíte do stroje, vyjde vám úhlová velikost zhruba 0,006 vteřiny (Neptun, pro srovnání, se nám v nejbližším bodě zobrazuje pod úhlem cca 2 vteřiny). Sirius je tedy (úhlově vzato) podstatně menší, ale zase silně září, takže ho na obloze najdete asi snadněji než Neptun.
Další příklady úhlových velikostí (angular diameter) najdete v polovině této stránky.
Článek je redakčně upravenou verzí blogového příspěvku na serveru
iDNES.cz. Publikováno s laskavým svolením autora.
Další díly a původní texty jsou dostupné na blogu Jana Řeháčka.




