Ne nadarmo se říká, že co se v mládí naučíš, ve stáří jako když najdeš. A platí to také o matematice. Více než kdy jindy to potvrzuje současná situace. Co říká matematika o koronaviru a jak správně interpretovat pojmy, které dennodenně slýcháme v médiích?
Pokaždé, když se začne mluvit o zavedení či zrušení povinné státní maturity z matematiky, přijde na přetřes výukový obsah matematiky na středních školách. Širokou veřejností pak rezonuje názor, že většinu z toho, co se na střední škole z matematiky musíme naučit, v reálném životě nikdy nepoužijeme. Průběh funkcí v tomto pohledu není výjimkou. Rok 2020 nás však už od března přesvědčuje o opaku.
S příchodem pandemie COVID-19 všichni očima hltáme aktuální matematické modely vývoje infekce a s nastraženýma ušima posloucháme jejich interpretaci prostřednictvím ministra zdravotnictví či hlavního epidemiologa. V těchto modelech se pracuje s několika matematickými pojmy, které jsou na jednu stranu známé každému středoškolákovi, ale na druhou stranu jen málokdo přesně ví, co znamenají.
Je potřeba děsit se exponenciálního průběhu?
Příkladem často skloňovaného matematického pojmu je exponenciální průběh, případně exponenciální růst. Současný ministr zdravotnictví Roman Prymula často mluví o potřebě „zbrzdit ten nárůst, aby opravdu nešlo o exponenciální růst, ale jen o lineární“. Možná je to jen důsledek snahy o zjednodušení, ale toto vyjádření je zavádějící – staví zde totiž proti sobě pojmy exponenciální a lineární růst. Důležité však je si uvědomit, že infekce obecně mají schopnost šířit se exponenciálně, protože se šíří z lidí na lidi. To znamená, že počet nově nakažených osob je závislý na počtu již nakažených, protože každá nakažená osoba může nakazit několik dalších. Z matematického hlediska jde o přímou úměrnost mezi již nakaženou populací a přírůstkem nově nakažených osob. Za vše může právě schopnost viru šířit se exponenciálně.
Na začátku každé infekce existují zpravidla pouze jednotky nakažených. Ty se ale následující den promění v desítky. A když denní přírůstky nakažených osob přesáhnou dvojciferné hodnoty, aby se v dalších dnech proměnily ve stovky, je většina veřejnosti zděšená, překvapená a plná obav. Na jednu stranu musíme připustit, že obavy jsou na místě – je více než pravděpodobné, že počty nakažených osob budou strmě narůstat. A pokud by křivka rostla příliš rychle, mohlo by dojít k selhání zdravotního systému, jako tomu bylo například v Itálii nebo ve Španělsku. Avšak z matematického hlediska jde o zcela přirozenou věc. Ať se budou počty nakažených osob vyvíjet jakkoliv, vždy půjde o exponenciální průběh. Takže i virus, který se šíří pomalu, se ve skutečnosti šíří exponenciálně. S tím nic nenaděláme.
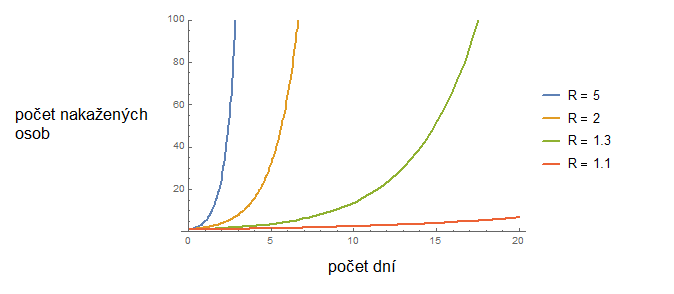
Abychom si udělali představu, zda pandemie ještě nedosáhla svého vrcholu, nebo zda je již na ústupu, není ani tak důležité sledovat počty nakažených osob, jako takzvané reprodukční číslo R, neboť právě to ovlivňuje rychlost exponenciálního růstu. Reprodukční číslo nám říká, kolik nově nakažených osob připadne v průměru na jednoho již nakaženého člověka. Například pokud jsme se před prázdninami dostali na hodnotu R = 0.5, znamená to, že na dva již nakažené lidi připadne pouze jeden nově nakažený. R = 1 znamená, že jeden nakažený člověk nakazí jednoho dalšího a až (pokud) se R dostane například na hodnotu 2, tak jeden nakažený člověk nakazí další dva lidi. Obecně můžeme říci, že čím bude R větší, tím bude šíření nákazy rychlejší a křivka nákazy (neboli exponenciála) poroste strměji. Jenže je podstatné si uvědomit, že infekce se bude šířit i další dny a (v případě R = 2) každý z těchto nově nakažených nakazí opět další dva. Tímto způsobem se bude nemoc šířit čím dál rychleji.
Klíčovým okamžikem v boji se šířením nákazy je hodnota R = 1. To je hodnota, ke které se ministr zdravotnictví v podstatě odkazoval. Zde se může zdát, že má šíření viru lineární průběh, neboť na jednoho již nakaženého připadá pouze jeden nově nakažený. Ale nemá. Stále se jedná o exponenciální křivku, pouze s koeficientem 1, a tudíž je její průběh v tomto okamžiku shodný s lineární funkcí. Z hlediska šíření viru jde však o důležitý milník, neboť jakmile hodnota reprodukčního čísla začne klesat pod 1, začne pomalu klesat i počet nově nakažených osob v populaci. I v tomto případě však půjde o exponenciální průběh křivky, ale tentokrát o exponenciální pokles. Zpočátku se počty nově nakažených budou snižovat po jednotkách, ale postupem času se situace bude vyvíjet čím dál příznivěji. Snad se toho brzy dočkáme a nepřijde mezitím ještě třetí vlna pandemie.
Budiž nám útěchou, že z matematického hlediska je nevyhnutelné, aby se exponenciální růst jednou zastavil a došlo zase k poklesu, protože počet nakažených osob nemůže růst do nekonečna. I kdybychom nezaváděli žádná opatření a nechali populaci takzvaně promořovat, měli bychom v jednu chvíli na planetě více nakažených osob, než nenakažených a křivka by začala samovolně zpomalovat. Bylo by totiž velmi pravděpodobné, že nakažený člověk potká další nakažené osoby (nebo osoby s již vytvořenou imunitu), a nemoc by se tudíž nemohla šířit dále.
Jak se počítá číslo R
Nutno přiznat, že i výše zmíněná interpretace čísla R je velmi zjednodušená. Nikdy totiž nemáme zaručeno, že každý nemocný přijde do styku pouze se zdravými jedinci a že je stoprocentně nakazí. Může existovat nemocný, který například vlivem okolností nikoho nenakazí a naopak nemocný, který půjde na oslavu a nakazí velký počet lidí. V případě hodnoty čísla R jde spíš o průměrný počet osob, který může nakazit již nakažený jedinec.
A ani samotný výpočet reprodukčního čísla není jednoduchá operace. Velmi zjednodušeně bychom si ho mohli představit jako podíl počtu nově nakažených osob s počtem již nakažených z předchozího dne. Ve skutečnosti ovšem existuje několik různých způsobů výpočtu hodnoty R. Navíc na vstupu výpočtu není jen počet nakažených osob z předchozího dne, ale za několik posledních týdnů. Díky tomu tak s číslem výrazně nezahýbají jednorázové výkyvy, jako byl například ten na Karvinsku. Svou roli při výpočtu reprodukčního čísla hraje také inkubační a infekční doba.
Častá nesprávná interpretace reprodukčního čísla je také ta, že téměř v reálném čase ukazuje účinnost opatření nebo dopad uvolňování. Ve skutečnosti má však na hodnotu čísla R vliv také inkubační doba nemoci, která může být v případě COVID-19 až dva týdny. Takže všechny výpočty ve skutečnosti zobrazují situaci v minulosti.
Šíření nákazy není jen o čísle R
I naprostému laikovi je jasné, že k šíření nemoci je zapotřebí, aby existoval někdo, kdo je nakažený a potkal se s dosud nenakaženým jedincem. Ať už tedy k tvorbě matematického modelu šíření nákazy používáme jakkoliv sofistikované metody, je neoddiskutovatelné, že pro rychlost šíření jsou důležité především dva faktory, a to nakažlivost nemoci (promítnutá do hodnoty čísla R) a počet lidí, kteří přijdou do vzájemného přímého kontaktu (tedy potenciální přenos). Zatímco nakažlivost nemoci je velmi těžké ovlivnit, neboť ta je závislá na imunitě daného jedince, případných mutací viru či nalezení vakcíny, ale třeba také na tom, jak pečlivě si kdo myje ruce, faktor potenciálního přenosu ovlivňujeme každý den tím, s kolika lidmi se setkáváme. Čím vyšší je počet lidí, s nimiž přijdeme do styku, tím vyšší je i pravděpodobnost přenosu nákazy a jejího šíření. Tento faktor se snaží vláda ovlivnit zaváděním různých opatření, ať už to je povinné nošení roušek či omezování počtu osob, které se mohou shromáždit na jednom místě.
A proto, neděsme se slova „exponenciální“, zkusme ho raději rozumně přijmout a současně pojďme udělat všechno proto, abychom pozitivně ovlivnili faktory, které ovlivnit můžeme, a reprodukční číslo snížili.