Co říká matematika o koronaviru a jak správně interpretovat pojmy, které dennodenně slýcháme v médiích?
Česká republika je od 5. října opět v nouzovém stavu. Křivka, která zachycuje počty nakažených, strmě stoupá. Pro mnoho lidí je rychlý nárůst na počátku epidemie velmi překvapující. Častým důvodem je neintuitivní pochopení pojmu exponenciální průběh, kterým jsme se zabývali už minule.
Mnozí očekávají, že počet nakažených bude každý den přibývat nějakým víceméně pravidelným tempem. Ale to je omyl. V momentě, kdy se v populaci objeví někdo nakažený novým druhem viru, obzvláště poměrně dost nakažlivým, jako je COVID-19, se virus šíří velmi rychle. Převážná část populace totiž proti němu zatím nemá vybudovanou imunitu, a tak je nárůst počtu nemocných exponenciální. Protože každý virus má v principu schopnost šířit se exponenciálně, je více než zřejmé, že počty nakažených budou přibývat. Otázkou je jak dlouho?
Abychom si udělali představu, zda epidemie ještě nedosáhla svého vrcholu, anebo už je na ústupu, není ani tak důležité sledovat naskakující čísla v celkovém počtu nakažených osob, ale hodnotu čísla R, tedy reprodukčního čísla. Toto číslo značí, kolik osob je v průměru schopen nakazit jeden nemocný. Čím je číslo větší, tím se nemoc šíří rychleji.
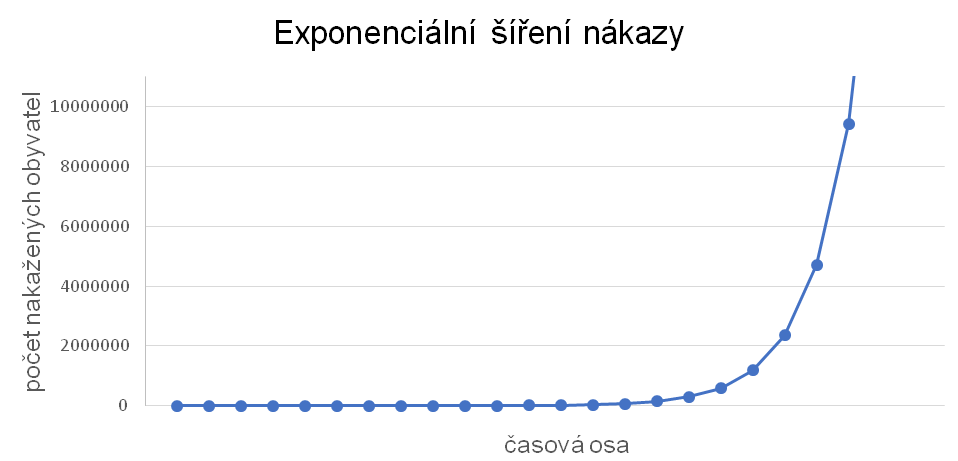
Uveďme si pro ilustraci hypotetický průběh epidemie v České republice. Na začátku března se objevily první tři případy, u kterých se prokázal pozitivní test na COVID-19. V tuto dobu se reprodukční číslo viru pohybovalo kolem hodnoty 2, což znamená, že jeden nakažený člověk může nakazit v průměru další dva lidi. Předpokládejme navíc, že nakažený jedinec je infekční během prvního týdne onemocnění. Exponenciální růst počtu nemocných znamená, že pokud se první den epidemie objeví 3 nakažení, v další fázi bude v České republice celkem 9 nakažených osob, poté 18, 36 a tak dále. Každý následující týden bude dvakrát větší přírůstek nově nakažených než předchozí týden. Tímto (exponenciálním) tempem máme na konci prvního měsíce skoro stovku nakažených, během čtvrt roku překročí počet nakažených osmnáct tisíc a do půl roku bude promořena celá republika.
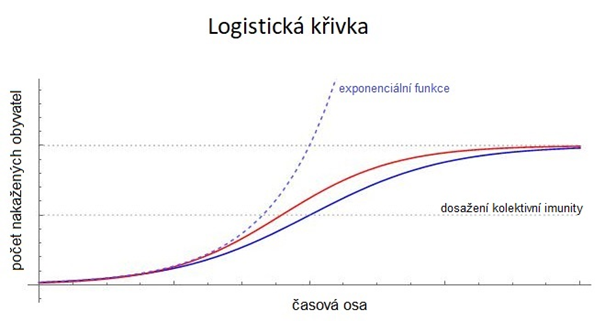
Logistická křivka
Realita ale není nikdy tak černobílá, jako jsou strohá čísla. Tento výpočet má několik nedostatků. Tím zásadním je, že ani kdybychom žádná opatření nedělali, šíření viru by se postupem času zpomalilo samo od sebe. Ve skutečnosti totiž nemůžeme předpokládat, že každý nemocný nakazí vždycky někoho dalšího. Spolu s tím jak se zvyšuje počet nakažených, klesá i počet lidí, kteří se ještě mohou nakazit. S postupným promořováním společnosti se zvyšuje pravděpodobnost, že nakažený potká opět nakaženého namísto zdravých lidí, a nemoc se tak nebude moct šířit dál takovým tempem.
Z toho důvodu v reálném světě exponenciály prakticky neexistují. Ve skutečnosti jde o takzvanou logistickou křivku. Na začátku má tato křivka průběh velmi podobný exponenciálnímu a je na ní vidět, že relativně rychle stoupá. Později se začíná růst zpomalovat, až se nakonec zastaví. Logistická křivka se používá, když chceme modelovat nějaký vývoj v čase, například pro modelování růstu populací a koncentrací v demografii, biologii, ekonomii, anebo když chceme zmapovat právě počty nakažených nemocí COVID-19 v populaci.
Tvar křivky, tzn. její exponenciální nárůst, případně pokles, závisí v případě epidemie na dvou faktorech. A to na již zmíněném čísle R - čím je hodnota reprodukčního čísla větší, tím graf roste strměji. A dále na dosažení takzvané kolektivní imunity, tedy stavu, kdy populace získá imunitu (ať už po onemocnění nebo po očkování či jinými způsoby) a šíření nemoci se tak samovolně zpomaluje. Uvádí se, že v případě nemoci COVID-19 se kolektivní imunity dosáhne při promoření 60 – 70 % obyvatelstva. Přepočteno na Českou republiku jde o zhruba 6,5 milionu obyvatel.
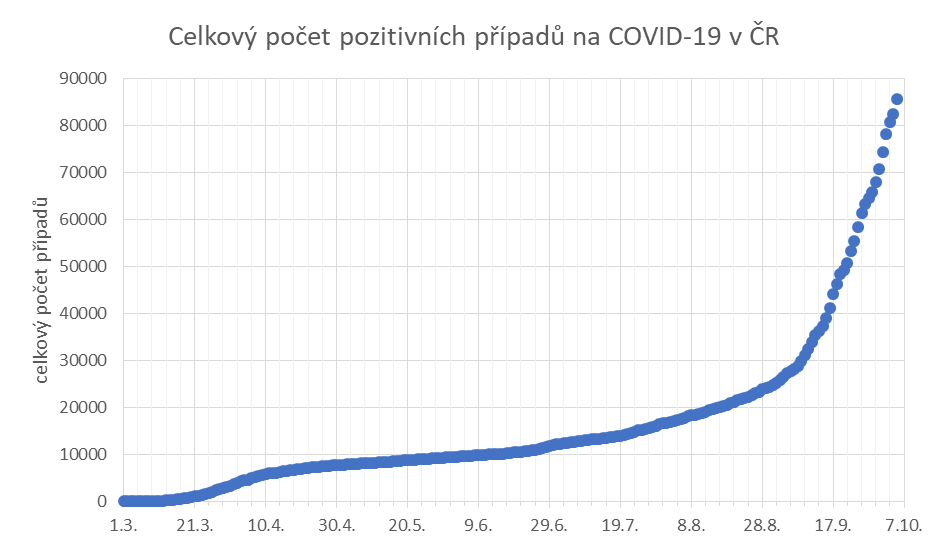
Z hlediska matematiky je rychlý nárůst počtu nakažených v začátku epidemie přirozený a měli bychom s ním počítat. Na druhou stranu v rychlosti onoho růstu tkví nebezpečí, neboť obrovský nárůst nemocných za tak krátký časový úsek může způsobit selhání zdravotního systému. Právě proto se zavádějí různá opatření, která mají exponenciálu zpomalit.
Zlom v boji proti epidemii nemusí znamenat jen to, že celkový počet nakažených vůbec neroste, nebo snad rovnou klesá. Je potřeba ho hledat jinde. Abychom si udělali představu, nakolik jsou tato opatření účinná a jak vypadá aktuální situace v boji s koronavirem, musíme se podívat na jiné grafy.
Denní nárůst počtu případů
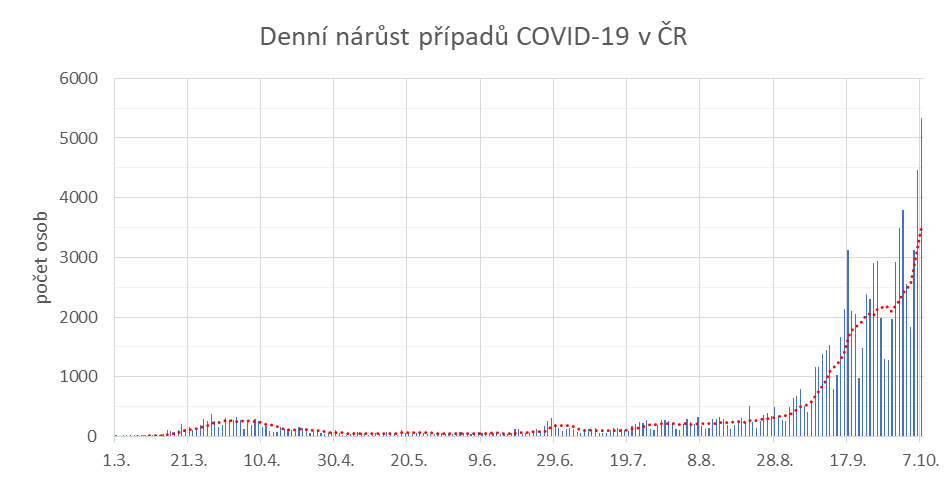
Daleko více informací o současném průběhu epidemie nám dokáže poskytnout graf, který zachycuje, kolik nových případů v zemi denně přibude.
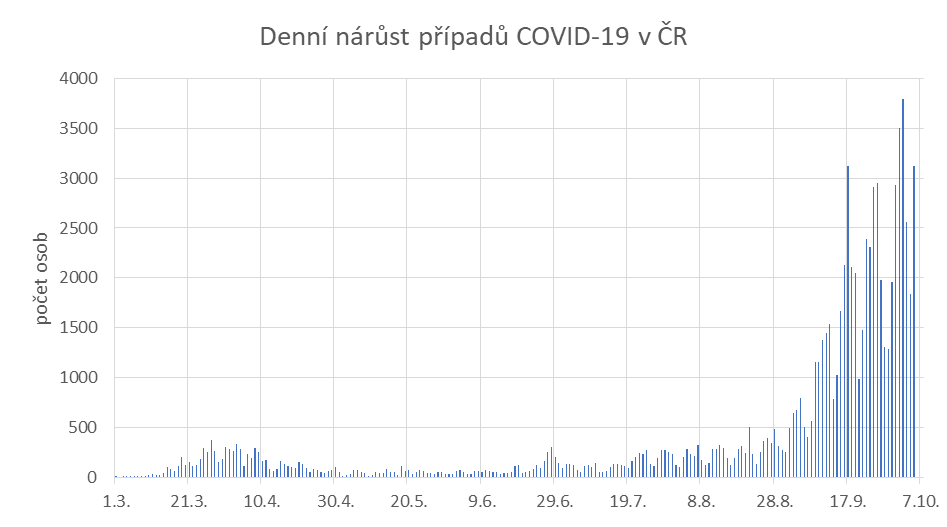
Tento graf již zobrazuje vývoj epidemie podrobněji. Dokonce z něj můžeme vyčíst, zda denní počet nakažených roste exponenciálně, anebo zda již začíná klesat. Exponenciální růst poznáme tak, že číslo značící počet pozitivních případů za daný den je vždy násobkem dne předchozího. Už při prvním pohledu na graf je vidět, že ještě nemáme vyhráno. Počet nakažených stále stoupá a patrně ještě nějakou dobu bude. Ačkoliv všichni netrpělivě čekáme na okamžik, kdy se dovíme, že denní počet potvrzených případů konečně přestal stoupat, nemusí to ještě znamenat, že máme vyhráno a noví nakažení již nebudou přibývat, vždy totiž může přijít další vlna epidemie, jako se to děje například teď.
Matoucí na grafu mohou být někdy jeho lokální výkyvy. To se týká také grafu, který zachycuje situaci u nás. Například v sobotu 3. 10. bylo pozitivně testovaných přes dva a půl tisíce osob, přičemž následující den klesl tento počet na 1 840, aby další den opět vzrostl na hodnotu přesahující tři tisíce nakažených. Čím byl onen nedělní pokles způsoben, můžeme jen odhadovat, jisté však je, že rozhodně neznamenal začátek vítězství nad epidemií.
Abychom se z podobných lokálních výkyvů předčasně neradovali, anebo naopak nehrozili, je dobré sledovat takzvaný sedmidenní klouzavý průměr neboli průměr nově nakažených osob za poslední týden. Jeho výhodou je, že zohledňuje právě dny, které statisticky vybočují tím, že je například provedeno méně testů anebo je naopak odhaleno ohnisko nákazy a počet případů nárazově naroste. Hodnoty grafu jsou u sedmidenního průměru ve srovnání s denními přírůstky víc vyrovnané, což nám umožňuje lépe vidět, zda křivka skutečně roste, klesá nebo si i přes nárazově vyšší (případně nižší) dny drží plochý tvar. Pokud se totiž stane, že v jednom dni počet pozitivních testů nárazově klesne, zatímco ve zbytek týdne tento počet roste, křivka sedmidenního průměru tímto jedním dnem nebude tolik ovlivněna.
Procentuální denní nárůst případů
Další graf, se kterým se můžeme setkat, popisuje, zda existuje nějaký trend ve vývoji nákazy. Zobrazená křivka značí, o kolik procent se počet potvrzených nakažených zvyšuje.
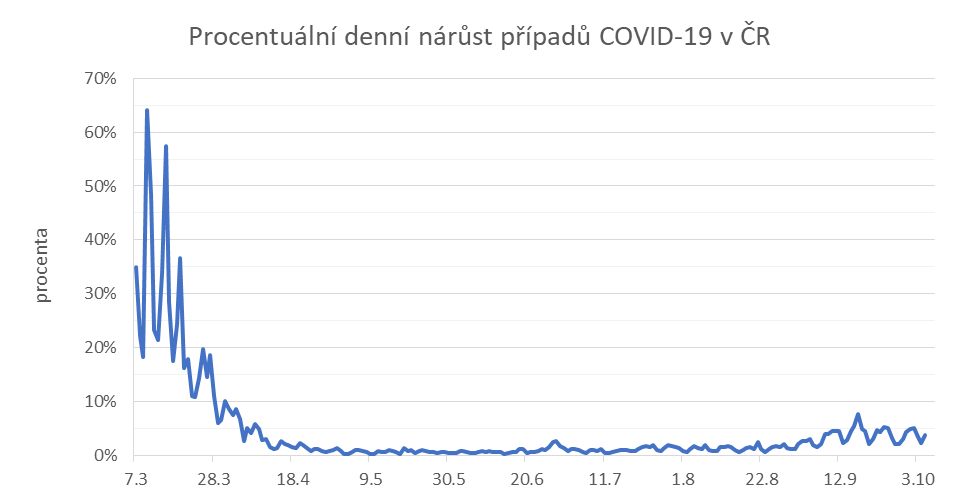
Pokud by nárůst měl zůstávat přirozený pro šíření viru, křivka by musela být zhruba vodorovná, tedy setrvat pořád například na 50 %. Pokud křivka klesá, znamená to, že se počet přenosů snižuje. Tedy jeden člověk už nenakazí tolik dalších jako na počátku epidemie a číslo R se snižuje.
Nenechme se zmást tím, že graf vyznačující denní přírůstky pozitivních případů může stále růst, kdežto graf vyznačující procentuální denní přírůstky nemusí dosahovat vysokých procent. Proto buďme obezřetní, pokud porovnáváme absolutní čísla s procenty - například nárůst 10 % z deseti tisíc je více než 50 % z tisíce. Základ, ze kterého procenta počítáme, je zcela zásadní. Proto na začátku epidemie dosahují procentuální denní přírůstky velké výkyvy – počítáme je z poměrně malého základu a tedy i přírůstky o jednotky obyvatel způsobí vysoké procentuální nárůsty.
A nakonec musíme mít na paměti, že na počet potvrzených nakažených má vliv také počet provedených testů. Obecně platí, že plošné testování je jedním z klíčových nástrojů k zastavení epidemie. Proto je snaha navyšovat počet odběrových míst či pořádat bezplatné vědecké studie. Testování jen malého počtu osob může mít za následek, že nám mnoho případů takzvaně proklouzne a tito lidé pak budou vir nevědomky šířit dál. Ani sebelepší graf nám pak neřekne, jak si v boji s koronavirem skutečně vedeme.
Pozn.: Článek byl 3. 11. upraven (exponenciální šíření nákazy bylo doplněno o infekční období, u logistické křivky byl doplněn pojem kolektivní imunita)