Metody strojového zpracování obrazu vycházejí z celé řady poznatků a matematických postupů. Hlavním cílem je přitom nalézt takové efektivní postupy, které umožní v reálném čase čili „rychle“ řešit úlohy rozpoznávání a analýzy nasnímané scény.
V současné době můžeme tyto metody nalézt v praxi třeba u mobilních telefonů, kde výrobci nabízejí stále nové a nové postupy získávání obrázků a jejich úprav. Tyto metody jsou mnohem více „odvážné“ a méně „konzervativní“ než ty, které se používají v průmyslových aplikacích, protože „novinky prodávají“.
Všechny informace, se kterými pracují počítače (a samozřejmě i mobilní telefony), jsou vlastně jen konkrétní, přesná čísla. Svět kolem nás je naproti tomu plný nepřesností. Jednou z metod strojového zpracování obrahu, která s vágností a nejednoznačnými pojmy, často obsaženými v lidské řeči, dokáže dobře pracovat, je fuzzy logika.
Aplikace fuzzy logiky
V klasické teorii množin jistý prvek do množiny buď patří, nebo nepatří. Fuzzy množina připouští částečné členství prvku v množině, takže prvku je v jistém intervalu přiřazena hodnota příslušnosti do fuzzy množiny. Velkou předností fuzzy logiky je potom také možnost překrývání jednotlivých funkcí příslušnosti.
Abychom nezůstávali jen u slovního popisu, znázorníme si na obrázku č. 1 trojúhelníkovou funkci příslušnosti, která slovně vyjadřuje nepřesnost hodnoty, například formulaci „číslo u je přibližně u0“ (pro upřesnění bychom mohli doplnit, že číslo u je jistě větší než a a jistě menší než b a čím více se hodnota čísla u přibližuje hodnotě u0, tím vyšší je jeho hodnota příslušnosti v množině).
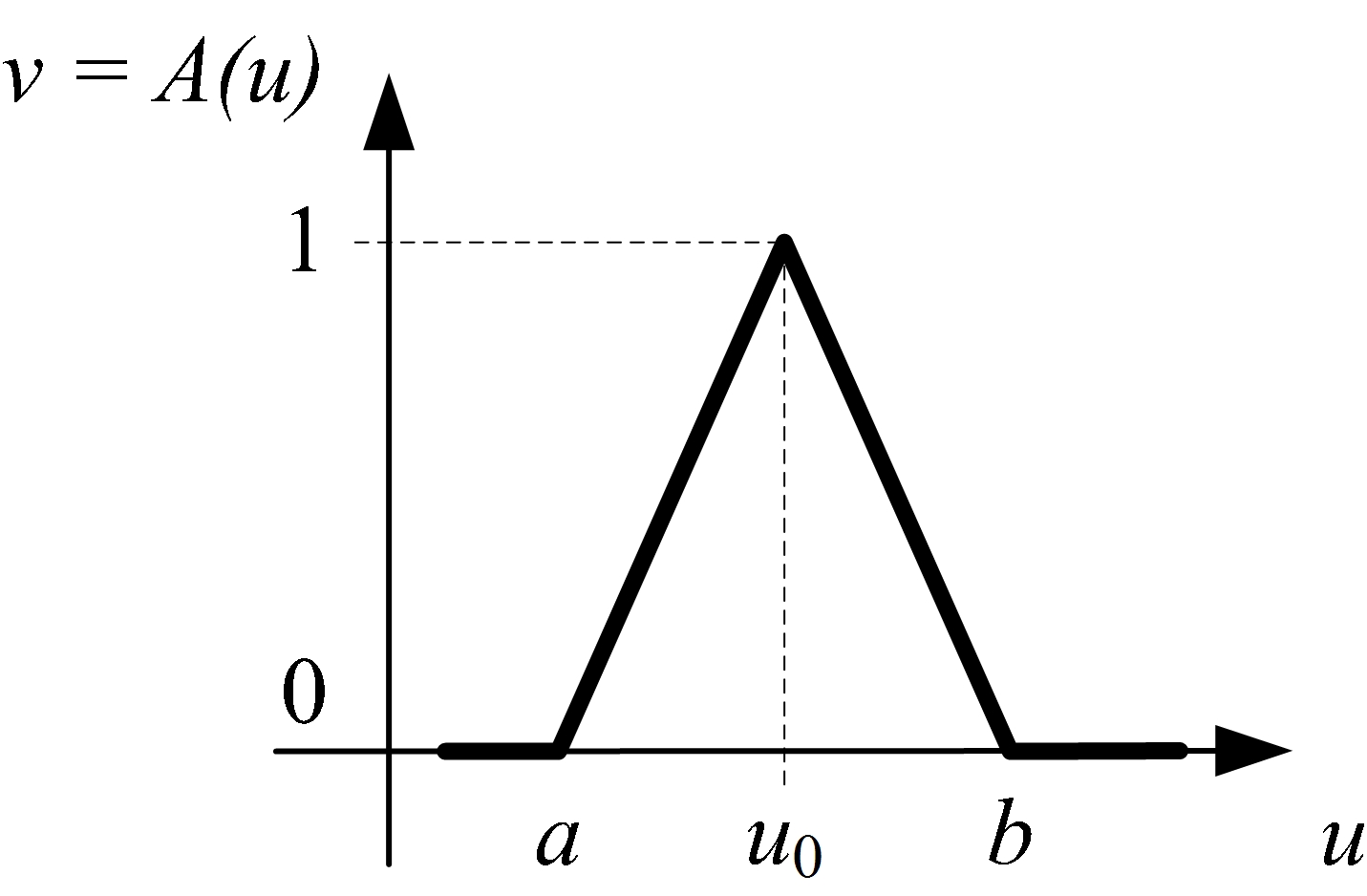 Obr. 1: Příklad funkce příslušnosti
fuzzy čísla „asi u0“
Obr. 1: Příklad funkce příslušnosti
fuzzy čísla „asi u0“
V oblasti strojového zpracování obrazu, který je složen z diskrétních obrazových prvků (pixelů) v rastru, lze metody fuzzy logiky aplikovat při hledání hran objektů v obraze, eliminaci šumu apod. Volba konkrétní funkce závisí na zkušenostech. Jednou z metod je tzv. fuzzy transformace (označovaná též jako F-transformace). Samozřejmě při vytváření vlastního výpočetního algoritmu se budeme snažit o jeho maximální efektivitu (tedy aby výpočet byl „co nejrychlejší“).
Na obr. č. 2 je vlevo znázorněn vstupní obraz, který máme dále zpracovávat. S využitím F-transformace provedeme hledání hran, tedy míst se změnou jasu v obraze, a následně další operaci (zde vyhlazení). Budeme samozřejmě vedeni snahou, aby všechny operace proběhly co možná nejrychleji, ideálně tzv. „v reálném čase“ (tedy „ihned“). V algoritmu pro hledání hran jsou použity dvě neurčité (fuzzy) hodnoty: „bílá“ a „černá“, jejichž pomocí klasifikujeme neurčité jasové hodnoty jednotlivých pixelů. Pixely označené jako „hranové body“ plníme jasovou hodnotou „nejvíce bílá“ (v našem případě 255).
 Obr. 2: Příklad práce s obrázkem
Obr. 2: Příklad práce s obrázkem
Nalezení hranových bodů nám může pomoci při další analýze scény, například při rozpoznání konkrétního objektu v obrázku. Při analýze obrazu ovšem velmi často vznikne problém s neostrými, rozmazanými nebo jinak nedokonalými snímky. Příkladem je první snímek z obr. č. 3, kde objekty vzadu jsou ostré, ale objekt vpředu je kvůli malé hloubce ostrosti optické soustavy rozmazaný. Je patrné, že změna úrovně jasu je v okolí hranových bodů rozmazaného objektu menší, než změna úrovně jasu v okolí hranových bodů ostrých objektů vzadu. Budeme aplikovat algoritmus pro F-transformaci a vhodnou volbou kroku můžeme získat vyšší míru rozlišení hran neostrého objektu, a tak i jeho hranové body.
 Obr. 3: Příklad aplikace F-transformace pro rozmazaný
obraz (zleva): původní obraz -> hledání vhodného kroku
aproximace I -> hledání vhodného kroku aproximace II -> aproximace s velkým krokem -> obraz s nalezenými hranami
Obr. 3: Příklad aplikace F-transformace pro rozmazaný
obraz (zleva): původní obraz -> hledání vhodného kroku
aproximace I -> hledání vhodného kroku aproximace II -> aproximace s velkým krokem -> obraz s nalezenými hranami
Aplikování nástrojů F-transformace umožní hledání objektů v obraze. Na obr. č. 4 je naznačena funkce algoritmu s využitím F-transformace (a zpětné F-transformace) při hledání hran v obraze. Vstupní obraz (zde označený jako f) je podroben F-transformaci (vznikne obraz F) a ten se „odečte“ od původního obrazu. Prahováním vzniklého obrazu e získáme obraz se zvýrazněnými hranami objektů v obrazu.
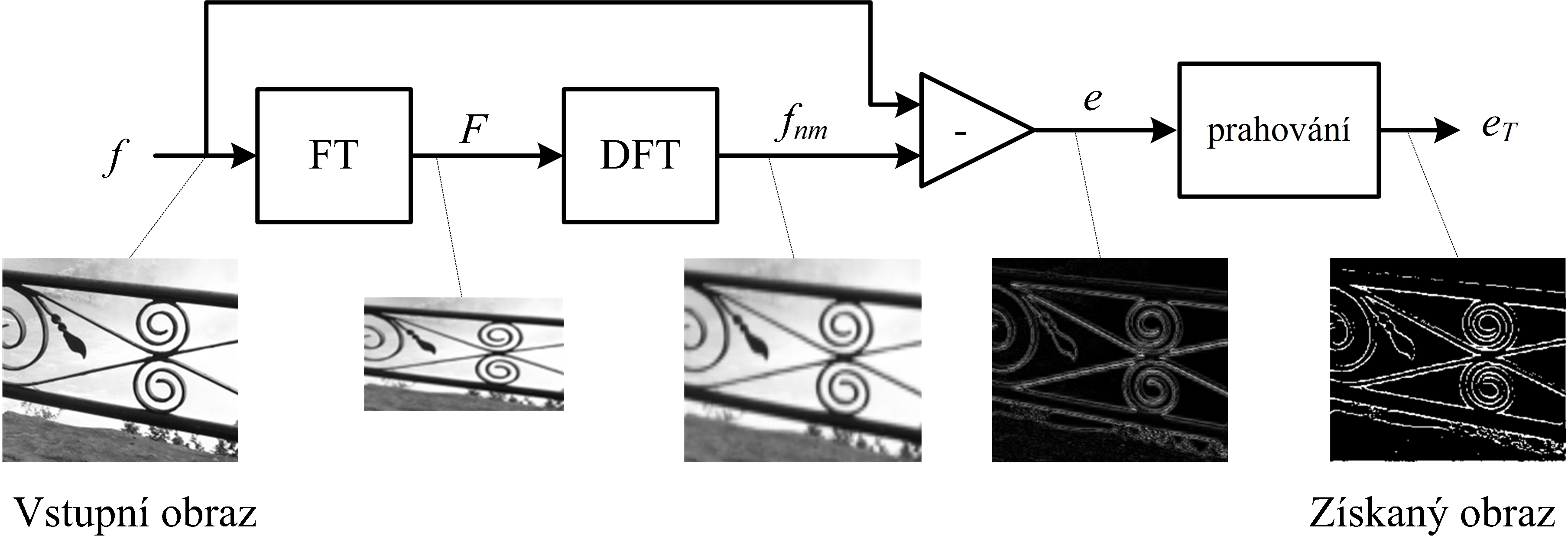 Obr. 4: Blokové schéma algoritmu pro detekci
hran
Obr. 4: Blokové schéma algoritmu pro detekci
hran
Aplikace metod využívajících fuzzy logiku nabízí velmi zajímavou alternativu a možnosti. Z uvedených příkladů je také patrné, že při strojovém zpracování obrazu je vhodné mít jisté zkušenosti a samozřejmě vhodné nástroje pro analýzu obrazu. V dalším díle se seznámíme s metodou práce při analýze obrazu, kdy není snadné získat jen jeden vhodný pohled na zkoumaný objekt a je vhodnější pracovat s pohledy několika. Této metodě se říká obrazová fúze.
Mohlo by vás zajímat:
Některé zajímavé metody strojového zpracování obrazu: Fuzzy logika
