Co nám dokáže říct moderní informatika o starověkých tělesech? Na takovou otázku se zaměřil Jan Hartman ve své bakalářské práci věnované barvení platónských a archimédovských těles. Absolvent v ní zkombinoval klasický problém a moderní metody vizualizace, a otevřel tak nové perspektivy v obou oblastech.
Představte nám, čemu jste se ve své práci věnoval?
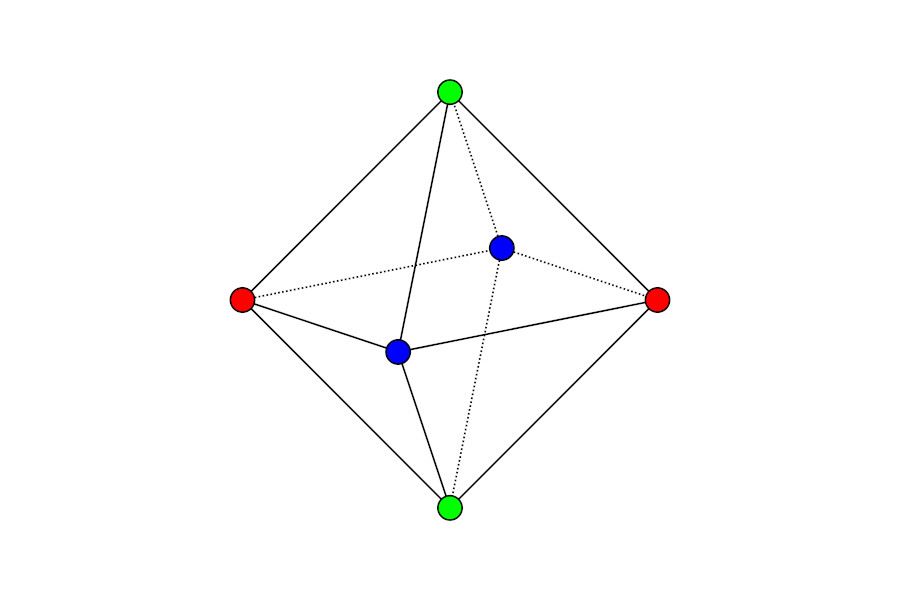
Ve své práci se věnuji barvení grafů platónských a archimédovských těles. Pod grafem nějakého tělesa si můžete představit trojrozměrnou síť, ve které jsou dva vrcholy propojeny právě tehdy, když mezi nimi vede hrana tělesa. Člověk pak může barvit vrcholy, stěny, nebo i hrany daného tělesa, ale já jsem se věnoval hlavně barvení vrcholů. Háček je v tom, že pokud jsou vrcholy propojené, nesmí mít stejnou barvu.
Zatímco platónských těles je celkem pět (čtyřstěn, krychle, osmistěn, dvanáctistěn a dvacetistěn), těch archimédovských je třináct a liší se tím, že na rozdíl od těch platónských mohou jejich stěny tvořit různé typy pravidelných mnohoúhelníků.
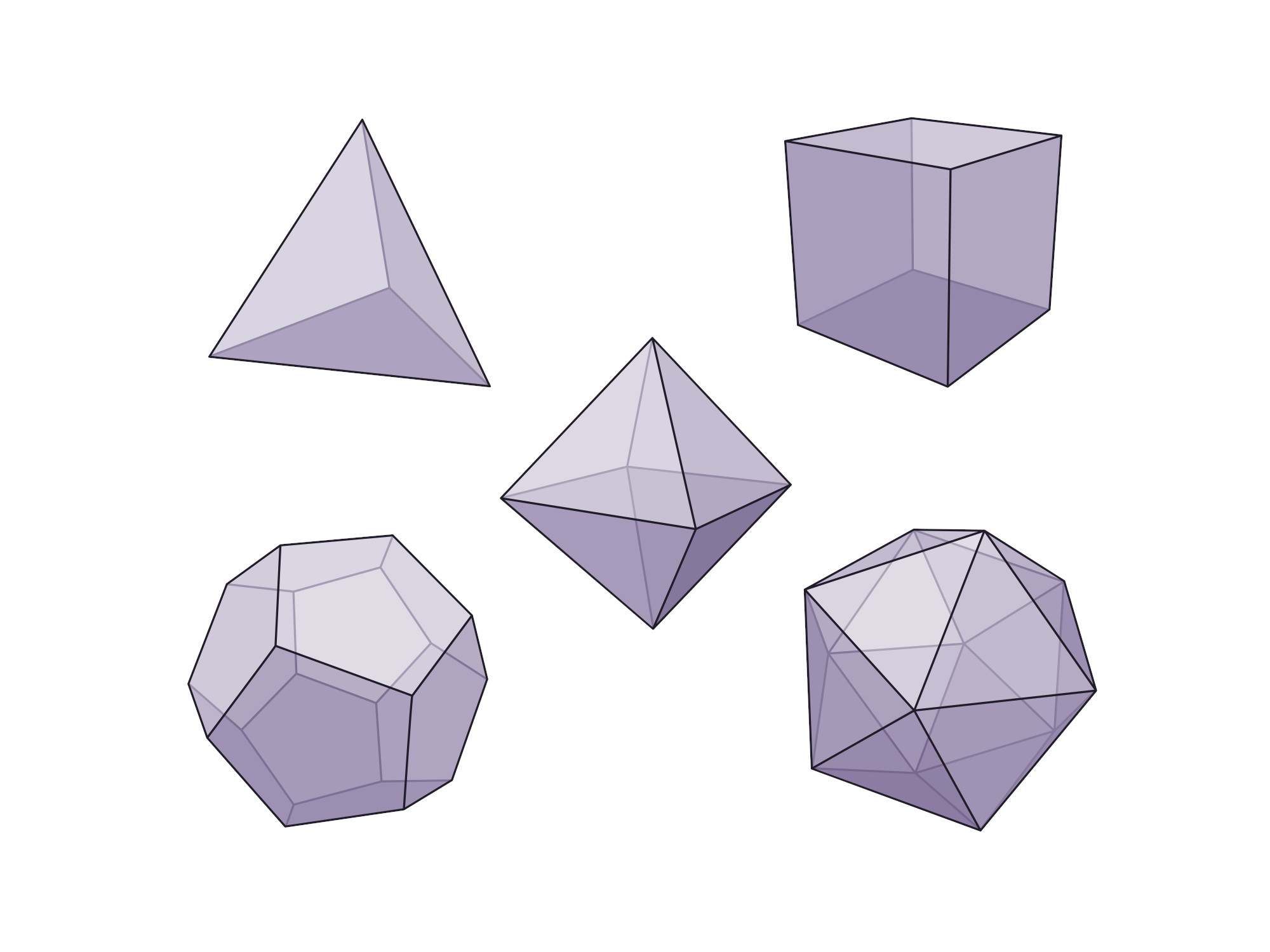
Pro připomenutí, stěny platónských těles musí všechny odpovídat právě jednomu vybranému pravidelnému mnohoúhelníku. Tato tělesa fascinují lidstvo již od starověku zejména svou bohatostí na symetrie. Například staří Řekové přisuzovali každému platónskému tělesu nějaký živel. Krychle reprezentovala zemi, dvacetistěn vodu, osmistěn vítr, čtyřstěn oheň a dvanáctistěn tzv. éter.
Právě tyto symetrie hrají v mé práci podstatnou roli. Hlavním cílem bylo totiž prozkoumat, kolik existuje různých obarvení vrcholů těchto těles, když vezmeme v potaz fakt, že některá obarvení mohou být jen rotací či „přezrcadlením“ jiných obarvení.
Co vás inspirovalo k tomu, abyste se zaměřil právě na toto téma?
Téma mě zaujalo hlavně tím, že kombinuje klasický problém barvení grafů s vysoce symetrickými trojrozměrnými tělesy. Barvení grafů si většinou spojujeme s větou o čtyřech barvách, která má následující populární interpretaci: Máme politickou mapu států a chceme státy obarvit tak, aby žádné dva sousedící neměly stejnou barvu. Z věty o čtyřech barvách vyplývá, že nám k tomu stačí pouze čtyři různé barvy. Všimněte si, že symetrie v tomto motivačním příkladu nijak nefigurují, což je škoda.
Podstatnou roli pro mě hrálo také to, že obarvení, která ve své práci počítám, se v mnoha případech dala přehledně vizualizovat. Tím pádem bylo možné podložit „suché“ výpočty pěknými obrázky a to mi jednoduše dělalo radost.
Jaký konkrétní přínos nebo využití má vaše práce?
Mým záměrem bylo spíše prozkoumat tuto hezkou část matematiky a prohloubit si v tomto směru své znalosti. Dle mého názoru má práce především estetický přínos – výsledky mi přijdou krásné a elegantní.
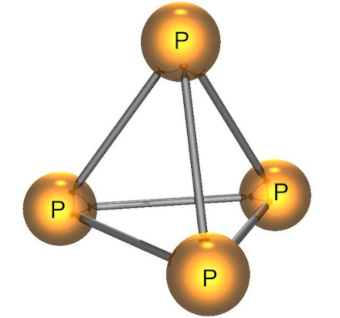
Platónská tělesa však můžeme najít skrytá ve stavbě molekul různých prvků. Například atomy fosforu v molekule bílého fosforu tvoří pravidelný čtyřstěn. A místo barev bychom si například mohli představit různé chemické prvky.
Jaké technologie a metody jste využíval?
Jelikož mi nešlo o rychlost běhu, ani o škálovatelnost mých programů, tak pro mě byl jasnou volbou Python. Konkrétně jsem pracoval především s knihovnou SageMath, která nabízí například funkce užitečné pro výpočty a vizualizace v oblasti teorie grafů. Také se mi hodily funkce pro práci s polynomy a algebraickými grupami. To ale není zdaleka vše, co knihovna SageMath poskytuje.
Co bylo při psaní práce nejtěžší? Je něco, co byste zpětně udělal jinak?
Nejtěžší pro mě bylo smysluplně strukturovat text tak, aby na sebe jednotlivá témata co možná nejplynuleji navazovala. V pozdější fázi mi také podstatnou část práce zabralo vymýšlení vlastních názvů a symbolů pro matematické relace, o kterých jsem chtěl psát, jelikož jsem nenašel žádné standardní, které bych mohl použít. Vymyslet výstižný název a k němu zavést smysluplné a intuitivní značení je pracnější, než se na první pohled zdá.
Jakým způsobem jste výsledky své práce ověřoval?
Stejným problémem jako já se zabýval i matematik Peter Cameron, ale ve své práci demonstroval výpočet pouze pro jeden konkrétní typ grafu. S jeho výsledkem jsem pak mohl porovnat výsledky mého algoritmu. Také díky menšímu počtu platónských těles a obarvení bylo možné správnost algoritmu ověřit manuálně.
Co považujete za nejdůležitější výsledek nebo závěr své práce?
Především to, že se mi povedlo implementovat algoritmus, který dokáže spočítat všechna hledaná obarvení a zároveň je pak systematicky vykreslit.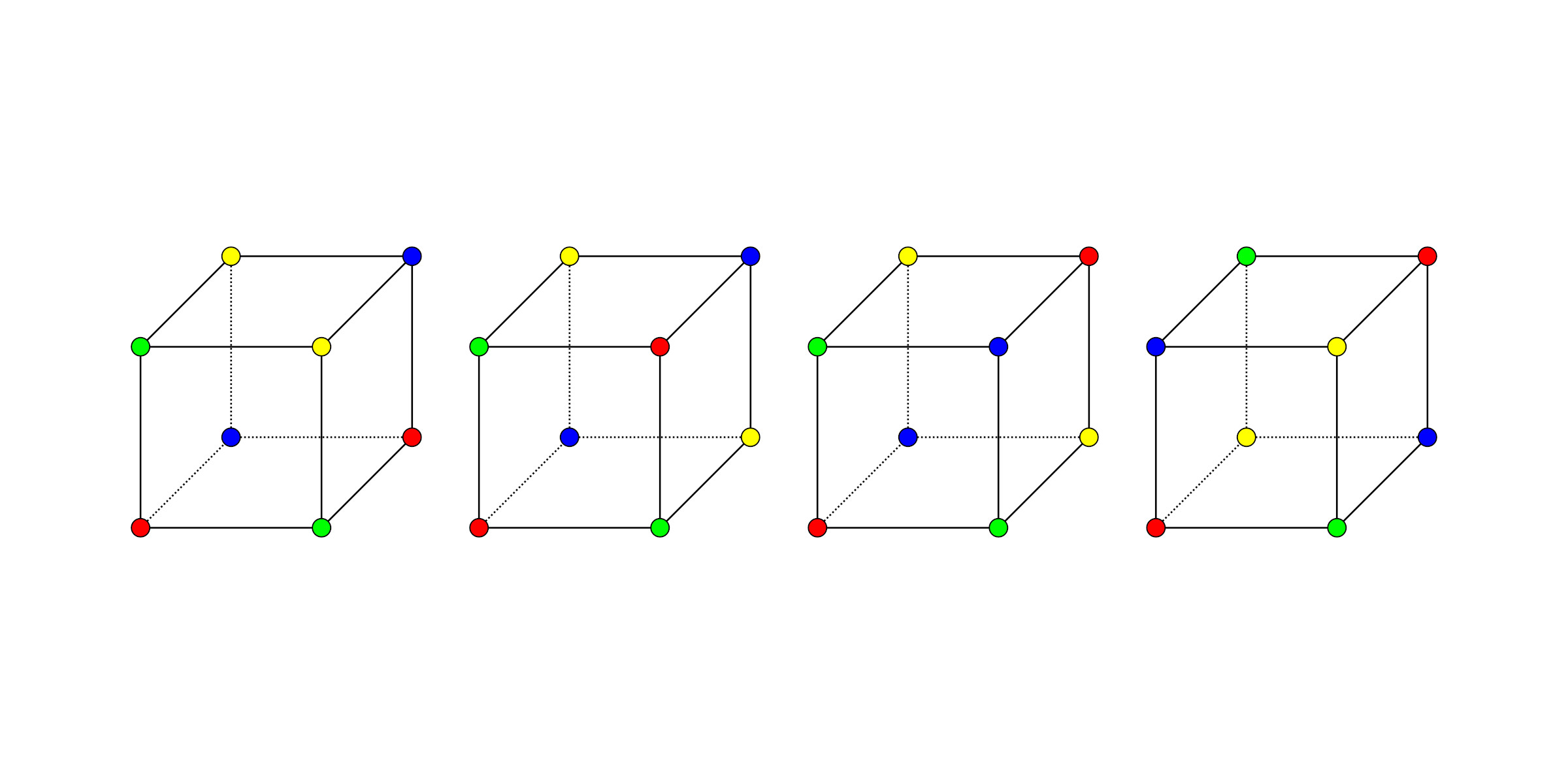
Máte pocit, že vaše práce může být inspirací pro další studenty nebo odborníky v dané oblasti?
Inspirací určitě být může. Konkrétně by bylo zajímavé pokusit se najít vzoreček, který by vyjadřoval počty hledaných obarvení. Tím pádem by zmizela nutnost obarvení generovat a počítat kolik jich je. Takový vzoreček ve tvaru polynomu máme, pokud nám stačí zohlednit pouze symetrie. Jakmile však chceme zohlednit zároveň i to, že některá obarvení jsou stejná až na prohození barev, tak na to žádný takový vzoreček zatím neexistuje.
Jaké jsou vaše plány do budoucna?
Plánuji dále pokračovat magisterským studiem oboru diskrétní modely a algoritmy u nás na MFF UK. Zároveň mi byla nabídnuta možnost vést cvičení diskrétní matematiky, na což se velmi těším. Pokud s tím budu mít dobré zkušenosti a pozitivní ohlasy, tak bych rád v budoucnu vedl více takových cvičení.
Odkazy:




