Papírová vlaštovka se silně podivným profilem křídla nerespektuje Bernoulliho rovnici o proudění. Přesto létá více než dobře. Třeba vás její výkony inspirují k letu neklidným letním vzduchem.
Pan Bernoulli promine, ale ono to opravdu letí. Málokdo by čekal, že se papírové letadélko s absurdním profilem křídla udrží ve vzduchu. A přesto to zvládá docela dobře, lépe než běžně známé vlaštovky. Sami si můžete zkusit jedno složit podle přiloženého návodu.
Všechno začalo někdy v polovině 60. let minulého století. Povoláním reklamní grafik Richard Kline se ve své newyorské kanceláři poněkud nudil a z dlouhé chvíle začal skládat netradiční papírové vlaštovky. Výkony jeho kluzáků se stále zlepšovaly. Protože nevěděl nic o mechanismu, kterým vzniká vztlak na křídle, byly nové druhy vlaštovek jen obrazem jeho vlastní fantazie, bez většího racionálního záměru.
Vystřihovánka letadélka ke stažení
Časem si překvapivých výkonů papírových letadélek všimli další lidé a začali jejich konstrukci zkoumat podrobněji. Nakonec zjistili překvapivou věc. Křídla odporují klasické představě o vzniku vztlaku. Připomíná to trochu slavný Edisonův bonmot, že kdyby znal Ohmův zákon, určitě by nevynalezl žárovku.
Jedním dechem však musíme dodat, že věda jen těžko může spoléhat na náhodu. Vynalezený profil je zkrátka výjimkou z pravidla. Právě proto si však zaslouží pozornost. Českým zájemcům tuto paradoxní vlaštovku poprvé představil Technický magazín v roce 1973 (T73, číslo 8, s. 54), který však přinesl poněkud jinou legendu o jejím vzniku. Pro celou věc to však není příliš podstatné.
Klínovitý Klineův profil
Konstruktéři podzvukových letadel od doby bratří Wrightů po současnost spoléhají na jev už dávno popsaný tzv. Bernoulliho rovnicí o proudění. Zjednodušeně z ní vyplývá, že v místech rychlejšího proudění je nižší tlak, než v místech s prouděním pomalejším. Profil klasického křídla je proto obvykle mírně vyklenutý směrem nahoru. Proudící vzduch musí po horní straně profilu urazit delší dráhu (proudí de facto rychleji) než po straně spodní, čímž na horní straně křídla vzniká podtlak (přesněji je na horní straně profilu nižší tlak než na spodní). Křídlo je pak nadnášeno díky rozdílu tlaků na horní a spodní straně. Realita je však mnohem složitější a svůj význam hraje také úhel náběhu křídla a další faktory.
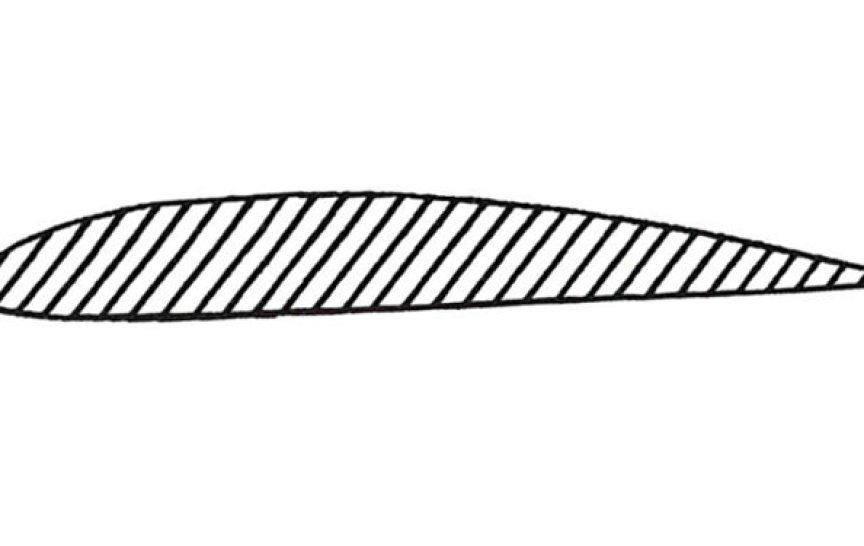
Klineův profil, který byl mimochodem patentován v USA pod značkou US3706430A, je v podstatě negací zažité konstruktérské představy. Jeho horní strana je tvořena rovinnou deskou, zespodu se klínovitě rozšiřuje a následně schodovitě prudce klesá. I při velmi malé rychlosti vytváří profil dostatečný vztlak na to, aby se vlaštovka úspěšně udržela ve vzduchu. Na pohled je to v přímém rozporu s výše řečeným.
"Rozpor je to jen zdánlivý," vysvětluje prof. Miloslav Feistauer z Katedry numerické matematiky MFF UK. "Důvodem může být skutečnost, že Bernoulliho model, z něhož vyplývá zmíněný paradox, je založen na předpokladu, že proudící vzduch je nevazká tekutina. Ve skutečnosti se i ve vzduchu projevuje viskozita, která může hrát důležitou roli."
To bylo potvrzeno odborníkem na aerodynamiku prof. Jaromírem Příhodou z Ústavu termomechaniky Akademie věd České republiky. Podle něho zde hraje důležitou roli viskozita a také tvar profilu. Za schůdkem totiž dochází k odtržení tzv. mezní vrstvy. V této oblasti je nízká rychlost proudícího vzduchu, což má za následek kladný vztlak. Vlaštovka tedy může letět.
Názor bychom však měli otestovat. V našem případě máme dvě možnosti. Jednak si můžete sami letadélko poměrně snadno sestavit a provést praktickou zkoušku, jednak nabízíme ještě trochu matematického modelování.
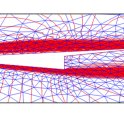
Vztlak na Klineově profilu ověřil na matematickém modelu prof. Vít Dolejší z Katedry numerické matematiky MFF UK: "Numerické řešení Navierových-Stokesových rovnic pro vazkou stlačitelnou tekutinu pomocí nespojité Galerkinovy metody dává kladný koeficient vztlaku, tedy výsledná síla profil křídla zvedá." Přiložený obrázek ukazuje isokřivky Machova čísla (poměr rychlosti tekutiny a lokální rychlosti zvuku) a trojúhelníkovou síť, na které proběhl výpočet. Je zde patrné odtržení mezní vrstvy na spodní části profilu.
Matematický model i praktická zkouška dokazují, že profil křídla, který v podstatě náhodou vynalezl Richard Kline, je funkční. Proč tedy konstruktéři nesáhli po této inovaci? Odpovídá opět prof. Příhoda: "Důvodem je tvar navrženého křídla, které je na obou koncích velmi tenké, a v důsledku možných vibrací indukovaných obtékajícím vzduchem by mohlo dojít k destrukci křídla. Kromě toho v důsledku špičaté náběžné hrany na přední straně křídla by při manévrování křídla za letu mohlo dojít naopak k zápornému vztlaku. Navíc při vysokých rychlostech by ostrá náběžná hrana měla za následek vznik nežádoucích rázových vln."
Další osudy
Richard Kline byl svým objevem nadšený dlouhou dobu. S dalšími experimentátory se pokoušel profil různě zdokonalit, zvětšovat jeho vztlak i jej přizpůsobovat reálným možnostem konstrukce. V 80. letech minulého století vydal dokonce knihu s návody na stavbu netradičních papírových letadélek The Ultimate Paper Airplane, z níž čerpáme i v tomto článku.
Každé zlepšování však s sebou přineslo další problémy, které omezovaly praktické využití. Původní představa, že profil bude stejně dobře sloužit při nízkých i nadzvukových rychlostech, se nenaplnila. Přesto však neupadl zcela v zapomnění. Relativně jednoduchá výroba zlákala letecké modeláře, z nichž někteří vytvořili i poměrně velké modely s tímto profilem.
Nakonec tedy zůstává Klineův profil spíše zajímavou rekreační hříčkou a zřejmě jedním z posledních vynálezů, které byly učiněny náhodou. V době, kdy nám reklama neustále nutí nějaké "letní inspirace", věříme, že inspiruje k letu neklidným letním vzduchem.
Matfyz.cz přeje všem čtenářům klidné a odpočinkové léto.