Prázdniny skončily, a tak je na čase trochu přitvrdit. Dnešní dávka aktualit obsahuje několik námětů k přemýšlení.
Nejnovější kvantový hlavolam – kvantoví holubi
Téměř celé století se studenti mučí snahou pochopit některé zdánlivě protismyslné závěry kvantové mechaniky, jejichž reprezentantem byla doteď tak zvaná Schrödingerova kočka, která může být podle kvantové mechaniky zároveň živá i mrtvá. Tento paradox formuloval v roce 1935 Ervin Schrödinger, aby poukázal na neúplnost kvantové teorie v oblasti přechodu mezi mikro- a makrosvětem.
Teď přišel mezinárodní tým fyziků s novým, stejně bizarním příkladem ze světa zvířat. Nazvali ho „efekt kvantového holubníku“. Je jasné, že když umístíte tři holuby do dvou holubníků, musí vždy být alespoň v jednom z nich dva holubi. Jenže podle kvantové analýzy, kterou tým provedl, žádný z holubů není schopen sdílet holubník s jiným holubem. A toto zdánlivě protismyslné tvrzení má dokonce i široké aplikace.
V klasické fyzice platí, že měření počátečního stavu nějakého systému může v principu říct vše o konečném stavu tohoto systému. V kvantové mechanice je to ale jinak. V roce 1964 učinil Yakir Aharonov objev, že v kvantové mechanice lze najít počáteční a konečné stavy systému, které jsou vzájemně zcela nezávislé. Aharonov spolu s týmem fyziků nyní použil toto zjištění a postuloval právě zmíněný „efekt kvantového holubníku“. Efekt se projeví, když pozorovatel provede posloupnost speciálních měření, během kterých zkouší umístit tři částice do dvou oddělených boxů. Napřed provede počáteční měření umístění částic (pre-selekci). Potom následuje mezilehlé zjišťování, zdali dvě částice sdílejí jeden box. Na závěr proběhne konečné měření polohy částic (post-selekce). Počáteční a konečné měření se dají uskutečnit zcela nezávisle. V mezilehlém kroku se dá provést tak zvané slabé měření, které sleduje všechny tři částice současně. Právě tehdy se ukáže, že žádné dvě částice nesdílejí společný box.
Důsledky těchto experimentů doplňují podle autorů známý Einsteinův-Podolského-Rosenův (EPR) paradox. V tomto scénáři se dvě částice, které začínají v jednom místě, stávají těsně spojené, a vznikne – teď v souvislosti s kvantovými počítači hodně probírané – kvantové provázání. Měřením stavu jedné částice se přitom ovlivní stav druhé částice i když jsou tyto od sebe vzdáleny tak daleko, že je vyloučeno jakékoliv ovlivňování způsobené efekty klasické fyziky.
Einstein kvantové provázání dokonce nazýval „strašidelným působením na dálku“. EPR je jedním ze základních objevů fyziky. Princip kvantového holubníku ho bude (pokud se jeho platnost prokáže) v jistém smyslu doplňovat. Tři částice mohou být na počátku separovány s nulovou korelací. Pak jsou uvedeny do kontaktu a nuceny interagovat vměstnáním do dvou boxů (holubníků). Během tohoto mezilehlého stavu jsou vázány silněji, než jak to dovoluje klasická fyzika. V koncovém stavu ale nejsou vázány vůbec.
Důsledky EPR paradoxu přispívají k porozumění informacím a základním fyzikálním zákonům hmoty. Autoři věří, že princip kvantového holubníku může být stejně důležitý. Vyplývá z něj totiž nová koncepce vzájemných souvislostí.
Autoři dokonce navrhují experimentální ověření své teorie. V experimentu budou tři elektrony procházet interferometrem. Ten rozděluje paprsek a určuje dvě oddělené dráhy pro elektrony, které se nakonec opět setkají. Protože existují pouze dvě možné dráhy, je možno očekávat, že minimálně dva elektrony budou sdílet jednu dráhu. Pokud tomu tak bude, budou blíž u sebe a nastane interakce. Jejich shodný elektrický náboj způsobí, že se budou odpuzovat, a jejich dráhy se budou odklánět. Tento odklon bude možno zjistit, jenže výpočty ukazují, že žádné dva ze tří elektronů nebudou sdílet stejnou dráhu a žádný odklon tedy nebude naměřen.
Tento experiment zatím nebyl proveden, autoři jsou si ale jisti svými výpočty. Jejich výsledky se některým fyzikům jeví jako „fascinující“, jinými jsou vehementně odsuzovány.
(Zdroj)
Nové solární články s uhlíkovými nanotrubicemi
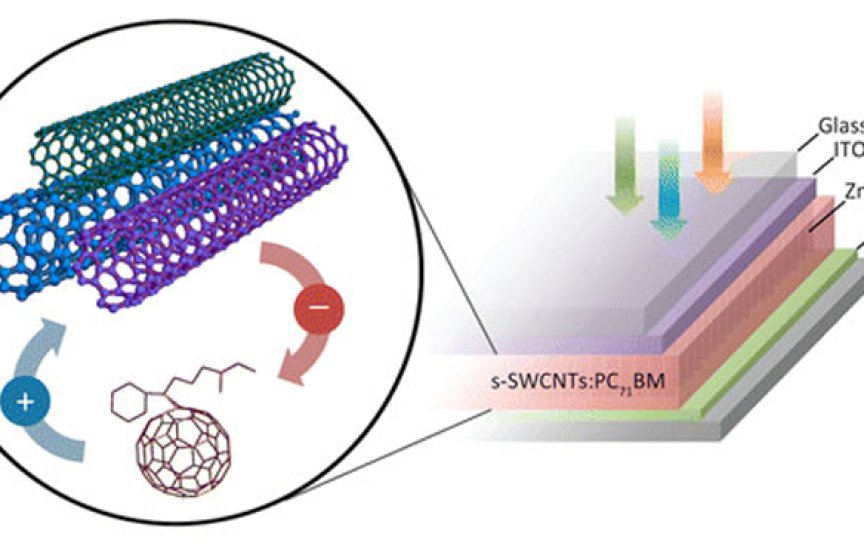
Fotovoltaické materiály ve formě tenkých vrstev jsou pro solární články výhodnější než tradiční materiály, jako je třeba křemík, protože jsou lehčí, ohebnější a levnější. Pracují tak, že ze slunečního záření zachytí foton a vytvoří pár elektron-díra (exciton). Aby vznikl elektrický proud, musí se elektron a díra rychle oddělit, jinak by se částice spojily a byly by znovu absorbovány materiálem.
Jednostěnné uhlíkové nanotrubice jsou ideálním materiálem, který absorbuje světlo v široké oblasti vlnových délek a ve kterém se nosiče náboje pohybují velkou rychlostí. Nevýhodou tenkovrstvých materiálů s nanotrubicemi jsou ale nízké hodnoty proudu a napětí, a tím i nízká účinnost přeměny energie.
Řešením by mohlo být využití jevu, který se nazývá chiralita. Pod tímto označením se skrývá asymetrie prostorového uspořádání molekul. Chirální je objekt, který není totožný se svým zrcadlovým obrazem. Američtí fyzici to zkusili a obešli problém nízkých hodnot proudu a napětí použitím polychirálních uhlíkových nanotrubic a fulerenů. Takové články absorbují světlo v širší oblasti spektra – zejména v blízké infračervené oblasti, kde zatím žádné běžně používané články nepracují.
Uhlíková nanotrubice je vrstva uhlíkových atomů pouze jeden atom silná, srolovaná do trubice o průměru kolem jednoho nanometru. Atomy tvoří hexagonální mřížku a relativní orientace mřížky k ose trubice tvoří její chiralitu. Právě v důsledku vícenásobné chirality absorbují takové články v širší oblasti spektra, což vede k vyšším hodnotám fotoproudu a vyšší účinnosti.
Nové prvky by mohly obnovit zájem o celouhlíkové sluneční články, které byly v poslední době poněkud zanedbávány. To, že nové články absorbují v širší oblasti spektra (včetně blízké infračervené), znamená, že by mohly být zvlášť užitečné jako aktivní prvky v článcích, které obsahují dva nebo více přechodů, z nichž každý absorbuje světlo jiné vlnové délky. Například přechody na čelní straně článku by mohly být zhotoveny z materiálu se širším zakázaným pásem, který by zachycoval energetičtější fotony, zatímco více se vyskytující fotony s nižší energií by mohly být zachycovány materiálem s užším zakázaným pásem, umístěným na zadní straně článku. Zkušební články dosahují účinnosti mezi 40 a 50 %.
A teď se podíváme na sluneční články a další zařízení z úplně jiného úhlu pohledu.
(Zdroj)
Superabsorpce by mohla vést k citlivějším kamerám, zdokonalit solární články nebo systémy pro optické komunikace aneb Nastoupí kvantové inženýrství?
Američtí fyzici už před časem objevili nový typ laseru, který emituje světlo kolektivně několika atomy. Jejich superradiační laser je založen na myšlence profesora Dickea z roku 1954. Robert Dicke nazval efekt „superradiací“. Vyskytuje se, pokud skupina emitorů světla, jako jsou atomy, molekuly nebo kvantové tečky vyzařuje světlo kolektivně rychlostí daleko vyšší, než stanovují pravidla klasické fyziky. Teď se k této myšlence znovu vrátil mezinárodní tým fyziků.
Emise a absorpce jsou vzájemně propojené jevy, takže systém, který vykazuje superradiaci, musí světlo také velmi dobře absorbovat. Tento jev se nazývá „superabsorpce“. Atomy, které jsou umístěné velmi blízko u sebe, mohou světlo absorbovat kolektivně. Potom není možno zjistit, který atom absorbuje určitý foton. Pokud taková skupina absorbuje foton, děje se to ve stavu kvantové superpozice všech možných excitovaných stavů, takzvaných Dickeových stavů. Přitom další absorpce vyvolává další takové stavy a každá superpozice navíc zahrnuje všechny možné způsoby, v nichž by se mohl vyskytnout úplný počet excitací.
Zvyšováním počtu Dickeových stavů se zvyšuje rychlost absorpce i emise. Protože podle kvantové mechaniky budou využity všechny možné způsoby dosažení excitace, pravděpodobnost uskutečnění události, která v našem případě znamená rychlost absorpce, bude úměrně růst.
Názorně: Dickeovy stavy tvoří určitý druh žebříčku s nerovnoměrně rozloženými příčkami, v našem případě různými rychlostmi absorpce. Stavy s polovinou atomů v excitovaném stavu mají největší počet možností uskutečnění absorpce. Aby bylo dosaženo maximální absorpce, je potřeba vybudit laserem právě tyto střední polohy.
Fyzici tento problém navrhují řešit použitím prstence molekul. Podobné prstence totiž používají rostliny při zachycování světla pro fotosyntézu. Geometrie prstence zajišťuje, že každé příčce Dickeova žebříčku připadá určitá frekvence světla, které může být absorbováno nebo emitováno. Tým ukázal, že pomocí kvantové mechaniky bude možno podpořit nebo potlačit přechody mezi jednotlivými stavy tak, aby se systém udržel na požadované příčce. To všechno by mohlo být realizováno umístěním superabsorberu do určitého vhodného prostředí, které omezuje nežádoucí přechody.
Co by to znamenalo prakticky? Pokud by se například udržovala optimální rychlost absorpce, mohl by být systém s kvantovou tečkou využíván jako detektor fotonů. Nanodráty by naopak mohly být využity k vytvoření pasti pro získávání zbylé energie, což by se zase hodilo v technologiích solárních článků a k přenosu optické energie.
Pokud budou překonány praktické překážky, může být tento nový přístup prakticky použitelný už v příštích letech. S pokračujícím technickým pokrokem je pouze otázkou času, kdy kvantové inženýrství nahradí klasické přístupy používané dnes. Podle fyziků totiž dozrál čas k tomu, abychom se naučili zapřáhnout kvantově mechanické kolektivní chování k ovládání fyzikálních procesů způsobem, který klasická fyzika neumožňnuje.
(Zdroj)
Práce byly převzaty z portálů arXiv, Nano Letters, Nature Communicetions
Další díly:
Aktuality z fyziky XVII
Aktuality z fyziky XVI
Aktuality z fyziky XV
Aktuality z fyziky XIV
Aktuality z fyziky XIII
Aktuality z fyziky XII
Aktuality z fyziky XI
Aktuality z fyziky X
Aktuality z fyziky IX
Aktuality z fyziky VIII
„Top
ten“ fyziky v roce 2014
Aktuality z fyziky VII
Aktuality z fyziky VI
Aktuality z fyziky IV
Aktuality z fyziky III
Aktuality z fyziky II
Aktuality z fyziky I
