Univerzita třetího věku (U3V), se kterou jsme se již seznámili, je skvělou příležitostí, jak jít s dobou i v seniorském věku. Posluchačům umožňuje seznamovat se s nejnovějšími poznatky z oblasti vědy, historie i kultury. Na Matfyzu budete moci v akademickém roce 2017/2018 navštěvovat v rámci U3V celkem devět kurzů z oboru fyziky, matematiky či výpočetní techniky. Jedním z nich je i Zajímavá matematika.
Proč vznikla daná odvětví matematiky? Jaký problém lidé v praxi řešili, že nastala potřeba vytvořit novou, do té doby neexistující část matematiky? Co se skrývá pod názvy matematických definic? V kurzu Zajímavá matematika si často klademe tyto a další podobné otázky, na které běžně ve škole nebývá čas. Vzniká tak pestrá mozaika témat, v níž se propojuje matematika s historií a aplikacemi.
Zabýváme se prakticky všemi oblastmi matematiky na úrovni střední školy (středoškolskou látku vždy zopakujeme) s mírným přesahem do matematiky vysokoškolské (ta je vždy srozumitelně vyložena). Vzhledem k velkému rozsahu témat kurz trvá dva roky. Oba ročníky jsou přitom na sobě nezávislé a je možné je absolvovat oba, či pouze jeden. Témata se vzájemně nekryjí, v druhém roce se věnujeme nové dosud neprobírané látce.
V prvním roce zpočátku zkoumáme elementární funkce: odmocniny, logaritmy, goniometrické funkce. Povíme si například, proč vznikla goniometrie v antice, k čemu tehdy sloužila, proč se jako „přirozený“ označuje logaritmus o podivném iracionálním základu e = 2, 71828182845904523536... Dozvíme se, jakým způsobem lidé počítali hodnoty odmocnin, sinů a logaritmů v době, kdy ještě neexistoval diferenciální počet, a zda mohou být tyto postupy inspirativní také v dnešní době.
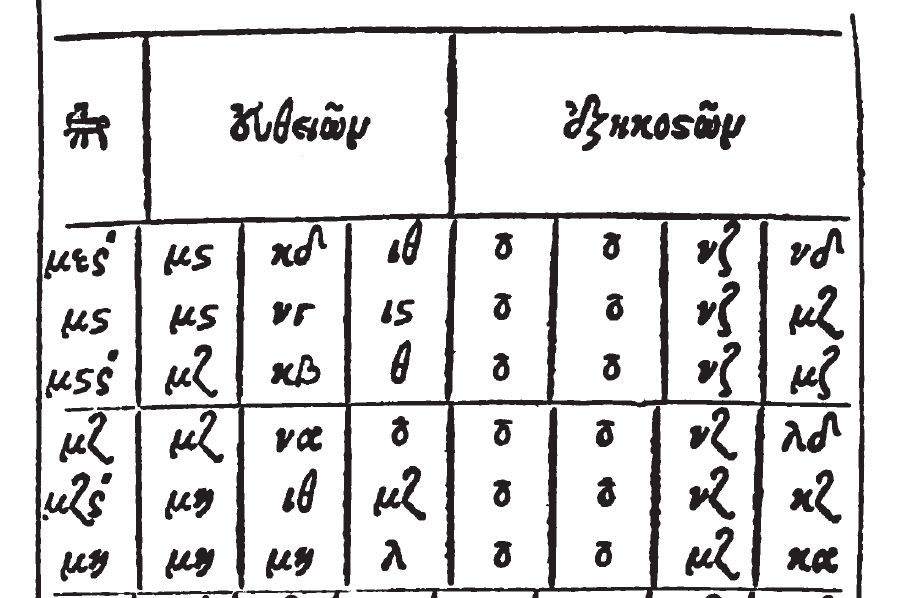
První tištěná tabulka hodnot předchůdce dnešní funkce sinus
(Grynaeus, 1538)
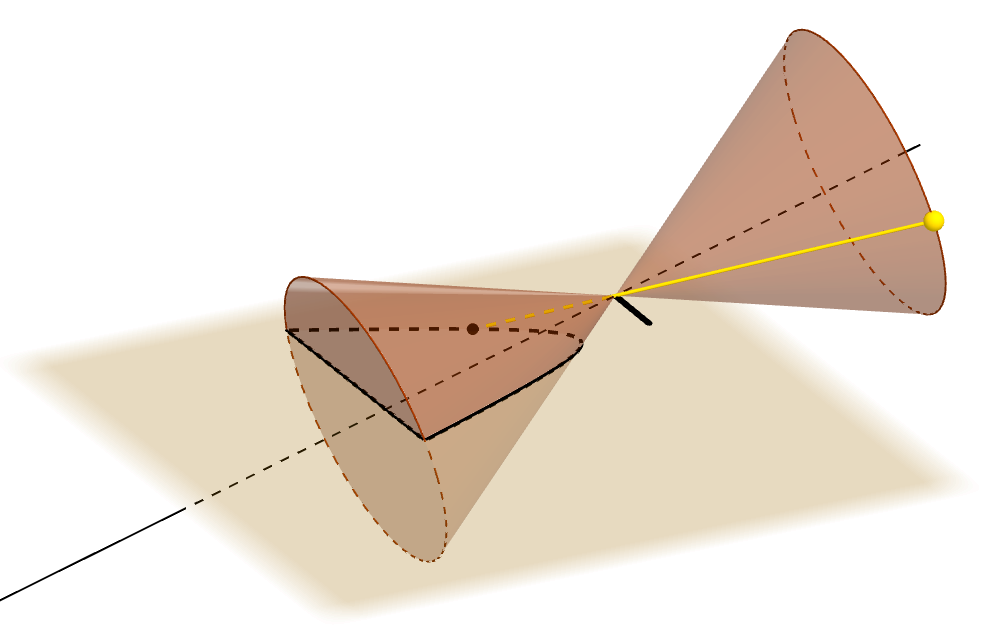
Druhým větším tématem v prvním roce je planimetrie. Řekneme si, proč v antice vznikla teorie kuželoseček. Dnes většinou známe kanonické rovnice
elipsy, paraboly a hyperboly, ale jaký příběh za těmito názvy stojí a kde
je vlastně ten kužel? Geometrie se, jak ostatně plyne z jejího názvu,
rozvíjela mimo jiné v souvislosti se zeměměřičstvím a s astronomií. Na
některé z dávných postupů se podíváme blíže, například na konstrukci
slunečních hodin.
Stín, který vrhá ukazatel slunečních hodin při pohybu Slunce po obloze v průběhu dne
Ve druhém roce se věnujeme vzniku a rozvoji diferenciálního a integrálního
počtu, s čímž souvisí také problematika definice a výpočtu obsahu a objemu. Inspirativní pro nás budou zejména postupy dochované u Archiméda ze
Syrákús a Eukleida z Alexandrie. Poté se seznámíme se základními
myšlenkami diferenciálního a integrálního počtu včetně
nejvýznamnějších aplikací (výpočty hodnot funkcí, elegantní formulace
fyzikálních zákonů atd.) Poměrně významnou epizodou je zde definice a výpočet čísla π, jehož dlouhé a barvité historii lze z velké části
porozumět právě se znalostí derivací. Derivace nám zase umožní seznámit
se prakticky s algoritmy. Díky nim totiž média čas od času referují o překonání rekordu v počtu vypočtených číslic čísla π.

Tělesa na páce, která sloužila Archimédovi při určování objemu
úseče rotačního paraboloidu
Protiváhou k matematické analýze je ve druhém roce algebra, zejména
jednotlivé číselné obory, k nimž se váže mnoho zajímavostí a historických souvislostí. Jmenovat můžeme například teorii řetězových
zlomků, která umožňuje získávat zajímavé výsledky jako například
předpovědět zatmění Slunce nebo určit, kolik tónů by měla mít hudba,
aby byla „dobrá“ (Zdalipak „naše“ hudba splňuje vypočtená
kritéria?). Podobně se budeme také ptát, proč vznikla teorie komplexních
čísel, která nemají tak názorný význam jako čísla přirozená,
racionální či reálná. Algebraickou část (a tím i celý dvouletý běh)
uzavírá řešení algebraických rovnic druhého, třetího a čtvrtého
stupně (tj. kvadratické, kubické a kvartické rovnice). Podíváme se na
důkaz neexistence obecného vzorce pro nalezení kořenů rovnice pátého a vyššího stupně, který by obsahoval pouze konečný počet čtyř
základních aritmetických operací a odmocňování. Právě tato otázka
stála u zrodu moderní algebry.
Kurzy U3V pořádané v akademickém roce 2016/2017 odstartují v týdnu od 3. října 2016. Přihlášky je možné podávat do 31. srpna. Bližší informace týkající se podávání přihlášek a přehled aktuálně vypsaných kurzů je dostupný zde.
Mohlo by vás zajímat:
Univerzita
třetího věku: Klima na naší planetě
Univerzita
třetího věku: Geometrie kolem nás
Univerzita
třetího věku: Fyzika pro nefyziky
Univerzita
třetího věku: Matematika ve starém Egyptě
Celoživotní
vzdělávání: Matfyz představuje Univerzitu třetího věku
