No tak dobře. Deskriptivu vám odpustím. Ale na sinus a kosinus se podíváme a při té příležitosti se seznámíme i s druhou základní matematickou konstantou – pí, mezi puberťáky známější pod přezdívkou „píčko“.
Jednoho dne se Alenka v říši divů probudila a ptáček, co všechno vycvrliká, jí hned po ránu prozradil, že srdcová královna přes noc mávnula kouzelným žolíkem a celá říše divů se několikanásobně zmenšila. Co ještě včera měřilo dva metry, mělo dnes na délku jen něco přes padesát centimetrů.
Alenka se začala podezřívavě rozhlížet kolem sebe, ale protože se sama také zmenšila, ničeho zvláštního si nevšimla.
Domy, které byly ještě včera desetkrát vyšší než ona sama, byly i dnes desetkrát vyšší. Vlk, který byl včera o polovinu nižší než Alenka, byl i dnes o polovinu nižší. A kaštan, který byl až do včerejška dvakrát rozložitější než topol nad řekou, byl stále dvakrát rozložitější než topol nad řekou.
Ani vzájemné úhly se nikterak významně nezměnily. Dvě větve kaštanu, které se včera křížily pod úhlem 35 stupňů, křížily se dál pod přesně tím samým úhlem. Držák lampy trčící kolmo ze stěny hostince s ní i nadále svíral vzorný pravý úhel. A dvě strany střechy spojující se podél hřebene v úhlu 60 stupňů, vytvářely i dnes přesně stejný úhel.
Jako by to mávnutí kouzelným žolíkem nezměnilo ani úhly, ani poměry velikostí.
„Kurióznější a kurióznější,“ pomyslila si Alenka.
Sinus a kosinus
Podobně jako Alenka v říši divů, staří Řekové před mnoha staletími zjistili, že rovnoměrným zvětšováním nebo zmenšováním trojúhelníků se zachovávají jejich úhly. Takovým trojúhelníkům říkáme podobné a platí pro ně, že i poměry jejich stran zůstávají neměnné, ať si máváme kouzelným žolíkem, jak chceme. Strana, která byla před zvětšením dvakrát delší, bude stále dvakrát delší. A tak antické vědátory napadlo tyto poměry pro podobné trojúhelníky tabulovat, aby se daly využít pro praktické účely. Například všechny trojúhelníky s úhly 40, 60 a 80 stupňů se budou lišit pouze svojí velikostí, ale poměry stran budou mít vesměs stejné. Pak bychom ze znalosti jedné strany mohli lehce určit strany druhé (což se hodí, pokud se druhé strany nedají změřit přímo).
Protože obecných trojúhelníků je příliš mnoho, omezili se Řekové při tabulování na trojúhelníky pravoúhlé. U těch totiž stačí znát jen jeden úhel a ty zbývající se snadno dopočítají (jeden je pravý a všechny dohromady musejí dát 180 stupňů).
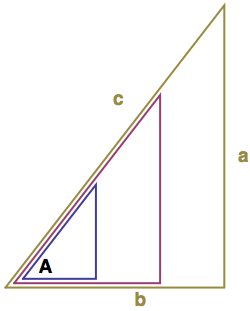
Na obrázku vpravo vidíme příklad skupiny podobných pravoúhlých trojúhelníků (ty větší jsou jen zvětšeninou nejmenšího modrého). Všechny mají úhel A vlevo dole, pravý úhel vpravo dole a úhel 90-A vpravo nahoře.
Všechny mají proto přesně stejné i poměry stran, takže stačí znát délku jedné strany, třeba c, a ty ostatní už si dopočítáme z poměrových tabulek. Pokud z nich například vyčteme, že pro tento úhel A mají příslušné podobné trojúhelníky poměr stran a ku c roven vždy a:c = 0,8, pak nám stačí vědět, že strana c měří 10 cm, a je jasné, že strana a bude splňovat a:10 = 0,8, a tedy bude dlouhá 8 cm.
Tím, že každému úhlu přiřadíme poměr odpovídajících si stran (který je pro všechny pravoúhlé trojúhelníky s daným úhlem stejný), tak z pohledu moderní matematiky vlastně definujeme funkci. Na vstupu zadáme úhel a na výstupu se nám objeví poměr určitých stran.
Stranám pravoúhlého trojúhelníku říkáme z pohledu úhlu A takto: c je přepona, b je přilehlá odvěsna, a je protilehlá odvěsna. Tyto tři strany můžeme spárovat do šesti různých poměrů, které budou odpovídat šesti funkcím. A těm souhrnně říkáme goniometrické (v angličtině též trigonometrické).
sin(A) = a:c (sinus je protilehlá ku přeponě)
cos(A) = b:c (kosinus je přilehlá ku přeponě)
tan(A) = a:b (tangens je protilehlá ku přilehlé)
cot(A) = b:a (kotangens je přilehlá ku protilehlé)
sec(A) = c:b (sekans je přepona ku přilehlé)
csc(A) = c:a (kosekans je přepona ku protilehlé)
V praxi se naštěstí používají pouze první tři. Ty zbylé uvidíte jen zřídka (třeba na výstavě matematických kuriozit). A kdo má kuriozity opravdu rád, může se mrknout na některé ještě starší verze trigonometrických funkcí.
Takto definované funkce mají ovšem jeden malý nedostatek. Omezují se pouze na úhly mezi 0 a 90 stupni. V pravoúhlém trojúhelníku nemůžete mít úhel větší než 90 stupňů. A tak dali matematici hlavy dohromady a sestrojili definici goniometrických funkcí, která se pro úhly mezi 0 a 90 stupni překrývá s tou původní, ale jinak je daleko obecnější.
Představte si bod pohybující se po jednotkové kružnici (viz obrázek níže) z počáteční polohy z (vpravo na ose x) proti směru hodinových ručiček (to je v matematice kladný směr). Polohu tohoto bodu můžeme v každém okamžiku přesně popsat pomocí úhlu, sevřeného odpovídající úsečkou v počátku: bod a odpovídá úhlu A a je jím beze zbytku určen, bod b odpovídá úhlu B atd.
Když si teď spočítáme, jaká je x-ová a y-ová souřadnice bodu a odpovídajícího úhlu A, zjistíme, že je to x = cos(A) a y = sin(A), protože ten vytečkovaný trojúhelník v pravém horním kvadrantu je pravoúhlý a jeho přepona je rovna jedné (kružnice je jednotková). Proto se zde přímo nabízí řešení dívat se na funkce kosinus a sinus jako na x-ovou a y-ovou souřadnici bodu putujícího po kružnici.
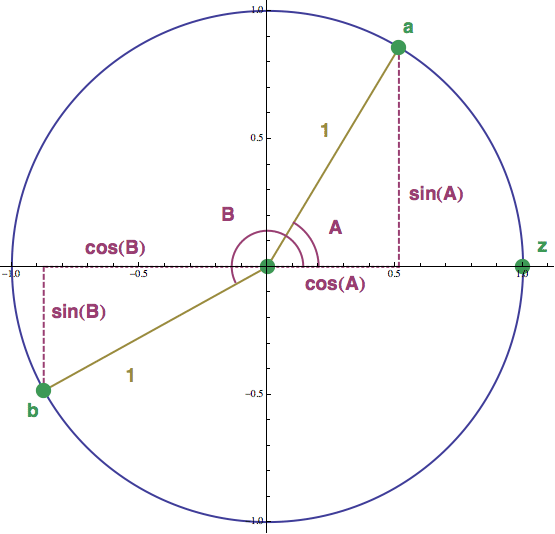
Takový přístup nám umožňuje definovat sinus a kosinus pro jakoukoliv
velikost úhlu A. Pokud je to třeba -500 stupňů, ať se nám panenky trochu
protočí, tak prostě s bodem z popojedeme o 500 stupňů po
směru hodinových ručiček (to je v matematice záporný směr) a tam, kde se zastavíme, odečteme souřadnice x a y a rázem
získáme hodnotu obou hlavních funkcí pro -500 stupňů. Zbylé funkce se pak
odvodí ze sinu a kosinu pomocí podílů (např. tan(x) = sin(x) / cos(x)), a nebo převrácených hodnot (např. sec(x) = 1/cos(x)).
Následující obrázek nám ukazuje graf obou základních funkcí (pozor úhel na ose x je v radiánech, takže jedno zakmitnutí modré sinusoidy není 360 stupňů, ale 2π radiánů, tedy cca 6,28...).
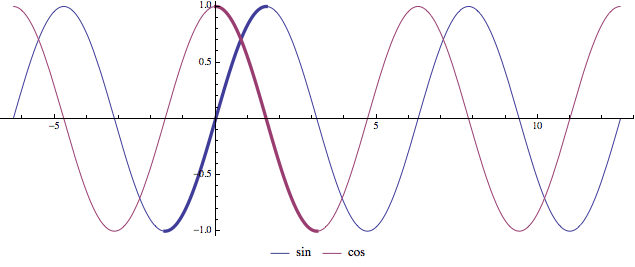
Je nasnadě, že takto zobecněné funkce se skvěle hodí k popisu vlnění
všeho druhu a ke studiu dalších periodických a oscilačních jevů. A kdekoliv se setkáte s kruhovým pohybem, jedna z těchto funkcí na vás
pravděpodobně taky vybafne.
Rozšířením definičního oboru na všechna reálná čísla jsme si ovšem zadělali na problém s inverzními funkcemi. Zatímco na základním intervalu od 0 do π/2 (pravý úhel) jsou obě funkce prosté, na celé reálné přímce už prosté nejsou, takže pro potřeby inverzních funkcí budeme muset zařadit zpátečku a definiční obor zase trochu zúžit, aby se nestalo, že dvě různé hodnoty x se zobrazí na jedno a to samé y.
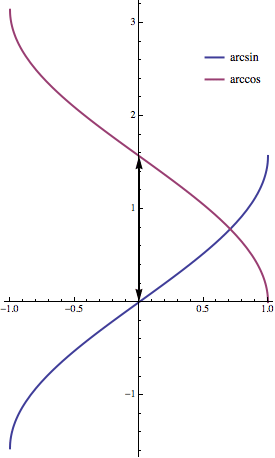
Jak to zúžení uděláme, je vcelku na nás. Nejčastěji se to provede tak, jak je naznačeno na obrázku výše. Části grafu jsou vykresleny tučně a ty reprezentují intervaly, na kterých příslušné funkce prosté jsou (základní interval je jejich součástí jak pro sinus, tak pro kosinus).
Na těchto intervalech už můžeme inverzní funkce lehce definovat (viz obrázek vpravo). Říkáme jim arkus-sinus (arcsin) a arkus-kosinus (arccos). Na některých kalkulačkách jsou také vyznačeny pomocí exponentu -1 (kterým se obecně označují inverzní funkce).
Když se vrátíme k trojúhelníkové definici, goniometrické funkce představují krabičku s trpaslíkem, kterému vhodíte dovnitř úhel a on vám vyhodí poměr určitých stran, zatímco inverznímu trpaslíkovi vhodíte na vstup poměr určitých stran a on vám na výstupu nahlásí úhel.
Přitom si všimněte, že pro obě inverzní funkce výstupní úhel na ose y obsahuje základní interval od 0 do 90 stupňů (od 0 do π/2 radiánů). Na obrázku je vyznačen černou dvojšipkou. Díky tomu můžeme vyřešit spoustu jednoduchých geometrických úloh.
Máme-li pravoúhlý trojúhelník s přeponou 3 cm a protilehlou odvěsnou 2 cm, bude poměr jejich délek 2/3. Pokud chceme zjistit úhel A, vhodíme poměr do inverzní funkce arcsin a vypadne nám 0,7297 radiánů (což je 41,8°).
Trocha magie
Protože sinus a kosinus jsou funkce definované geometricky, matematiky zajímalo, jak by se daly zapsat pomocí jednoduchých algebraických operací s proměnnou x, tedy zda by se daly vyjádřit jako kombinace jejích mocnin. Ukázalo se, že jsme-li ochotni připustit nekonečný součet, tak to skutečně lze, a to pomocí tzv. MacLaurinových řad (kromě sinu a kosinu jsem si jako ukázku vybral ještě přirozenou exponencielu a arkus-tangens). Když si to rozmyslíte, tak rovnice (2) a (3) jsou docela překvapivé: celou geometrii můžeme hodit za hlavu a definovat sinus i kosinus čistě pomocí mocnin proměnné x (úhel v radiánech). Poslední vzoreček (5) je trochu z jiného soudku, ukazuje totiž, jak se sinus dá rozepsat pomocí součinu.
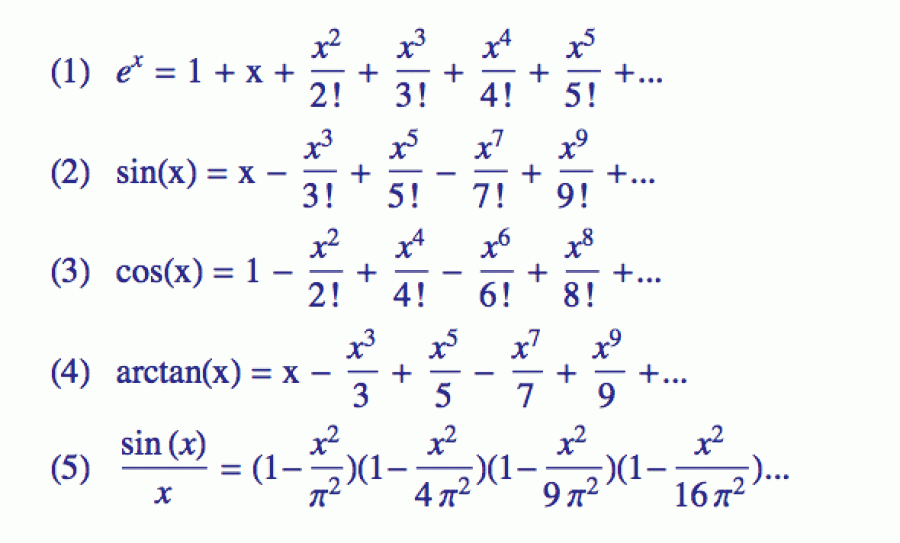
Teď možná přemýšlíte, proč matematici trvají na tom, že by úhly měly být vyjádřeny v radiánech. Částečně je to proto, že vzorečky ve stupních neplatí (respektive musely by se tam přimalovat všelijaké vyrovnávací konstanty). Obecně platí, že pokud manipulujete pouze s úhly, můžete použít jednotky dle libosti. Tam, kde ale mísíte v jednom vzorečku úhly (x) a poměry stran (sin(x)), je nutno použít radiány (radiány vlastně také reprezentují určitý poměr - je to délka kruhového oblouku odpovídající danému úhlu ku poloměru příslušné kružnice).
Zatím vás nebudu unavovat tím, jak se formulky odvodí (k tomu se časem dostaneme), ale podíváme se, jak vlastně fungují. Pravé strany si můžete představovat jako aproximace daných funkcí s tím, že čím více členů si vezmete, tím lepší aproximaci získáte.
Vezměme si například úhel x = 0,48 (radiánů). Sinus tohoto úhlu je 0,46178, a pokud si vezmete první tři členy vzorečku (2) a dosadíte x, dostanete prakticky totéž číslo. Ovšem pro vyšší x se aproximace postupně zhoršuje. Pro x = 1,8 (radiánů) dostaneme sin(x) = 0,973848, zatímco první tři členy vám dají 0,985464. Přidáte-li ale čtvrtý člen, dostanete 0,973317, a s pátým už jsme skoro doma: 0,973863.
K čemu jsou takové piškuntálie dobré? Jednak k tomu, abychom se o funkcích něco dozvěděli, a jednak proto, abychom se následně něco dozvěděli o konstantě π. Tato mystická konstanta lidstvo fascinovala už od dob starých Sumerů a to, že plný úhel (měřený v radiánech) má hodnotu právě 2π naznačuje, proč číslo π ovládá velkou část matematiky. Sinus - jedna z nejdůležitějších funkcí - má totiž kořeny (hodnoty x, pro které je sin(x) roven 0) přesně v násobcích 180 stupňů a to jsou v radiánech právě násobky π.
Pomocí těchto kořenů si můžeme ten nekonečný polynom (2) rozložit na kořenové činitele, a tím získáme další zajímavé vyjádření funkce sinus v podobě rovnice (5). Ta nevyjadřuje sinus jako součet mocnin, ale jako součin určitých kvadratických členů (přičemž každý z nich se dá dále rozložit na dva lineární, které si můžeme představit jako zmíněné kořenové činitele).
Abychom do toho lépe viděli, zopakujme si nejdřív, jak rozklad na kořenové činitele vlastně vypadá. Vezměme si třeba kvadratický polynom:
p(x) = x² + x – 6
Ten má dva kořeny (hodnoty, pro které je polynom roven nule), a to x = 2 a x = -3, takže ho můžeme zapsat jako součin kořenových činitelů x-a, kde a je jeden z kořenů (nezapomeňte, že kořeny od x odčítáme, aby se polynom po dosazení kořene vynuloval). Občas můžeme kořenové činitele zapsat podobně jako ve formulce (5): (1-x/a). To se hodí hlavně u nekonečných rozvojů, protože takový činitel pak v součinu lépe konverguje. I tento tvar se vynuluje po dosazení x = a. Takže máme:
p(x) = (x-2) (x+3) a nebo alternativně: p(x) = -6 (1 - x/2) (1 + x/3)
Sinus má kořenů sice nekonečně mnoho, ale zase se nemusíme otravovat s kvadratickou rovnicí, protože přesně víme, kde se nalézají (v celočíselných násobcích pí), takže sestavit kořenový rozklad (5) zase není tak těžké. Nezapomeňte, že podle vzorečku A2 - B2 = (A-B) (A+B) ten první člen vlastně reprezentuje součin kořenových činitelů pro π a -π, druhý pro 2π a -2π, třetí pro 3π a -3π a tak dále. Pokud vás znepokojuje, že na pravé straně není člen odpovídající tomu nejzákladnějšímu kořenu (x=0), pak vězte, že je obsažen ve členu (x-0), kterým jsme celou rovnici vydělili – proto je nalevo sin(x)/x.
Rovnice (5) tedy není nic jiného než rozklad sinu na kořenové činitele (neboli faktorizace funkce sinus). Tohle bylo intuitivně jasné už v 18. století Leonardu Eulerovi, ale opravdový pořádek v tomto problému udělal o století později až německý matematik Karl Weierstrass.
Eulerovi to však stačilo k tomu, aby v roce 1734 sečetl nekonečnou řadu reciprokých čtverců (a tím vyřešil tzv. Basilejský problém). Udělal to celkem fikaně.
V první řadě si vzal formulku (2), vydělil ji x (takže nalevo dostal sin(x)/x) a všiml si, že koeficient stojící u x2 je přesně -1/6. A pak se podíval na formulku (5) a řekl si, že stačí pravou stranu pečlivě roznásobit, podívat se, jaký je koeficient stojící u x2 a položit ho roven -1/6, protože v obou případech jsme do nekonečného polynomu rozvedli funkci sin(x)/x. Roznásobení je samozřejmě po čertech těžké, protože máme nekonečně mnoho členů, ale Euler si uvědomil, že nás nezajímá, jaký bude celkový výsledek roznásobení, ale pouze to, jaký bude koeficient u druhé mocniny x. A to se zjistí daleko snáze.
Když se na výraz (5) dobře podíváte, zjistíte, že jediný způsob, jak při roznásobování dostat x2, je vybrat si z jedné konkrétní závorky člen obsahující x2 a ze všech ostatních závorek jedničku. Jinak si tu druhou mocninu prostě nenabrnkáte. Takových členů ale bude celá spousta...
A tak se milý Euler pustil do díla a začal si členy obsahující x2 zapisovat:
- x2/π2 - x2/4π2 - x2/9π2 - x2/16π2 - x2/25π2 - x2/36π2 - x2/49π2 - ...
Po roznásobení celého nekonečného součinu dostanete pochopitelně i kupu jiných členů, ale ty budou mít jinou mocninu x, a proto nás nezajímají.
Když z toho všeho vytknete x2 a položíte to, co vám po vytknutí zbyde (to je ten koeficient) rovno -1/6, dostanete následující rovnici:
- 1/π2 - 1/4π2 - 1/9π2 - 1/16π2 - 1/25π2 - ... = -1/6
Rovnici teď vynásobíme -π2 a dostaneme slavný Eulerův součet (první řádek):

Abyste si nemysleli, že to je jediná nekonečná řada, jejímž součtem je výraz obsahující Ludolfovo číslo, připojil jsem ještě další dva příklady. Ten na prostředním řádku dostanete tak, že nahoře do formulky (4) dosadíte x = 1 a uvědomíte si, že arctan(1) je π/4 (neboli 45 stupňů). Tahle řada ovšem konverguje velice pomalu, a tak se pro praktický výpočet pí používá spíš řada uvedená na řádku posledním. Ta konverguje podstatně rychleji (tedy potřebujete méně členů k tomu, abyste získali pí na určitý počet desetinných míst).
Pro srovnání: když si spočítáte π podle prvních deseti členů každé řady, dostanete pro první 3.057, pro tu druhou 3.232 a pro třetí 3.141.
To, že se π vyskytuje v kořenovém rozkladu funkce sinus, se dá pochopit. Koneckonců, funkce je odvozena z pohybu po kružnici a kde kružnice, tam pí. Ale to, že se pí dá odvodit z celočíselných řad, ukazuje, že toto číslo hraje v matematice podstatně fundamentálnější roli než jen jako pomůcka při studiu kulatých nesmyslů (další zajímavé vztahy pro pí najdete zde).
Trocha poezie
Od té doby, co se lidstvo naučilo počítat píčko na mnoho desetinných míst, našli se dobrodruzi, kteří se tu řadu čísel chtěli naučit nazpamět, aby tím mohli ohromovat frekventantky odborných hrnčířských učilišť.
Podle Guinnessovy knihy rekordů je držitelem světového rekordu v biflování desetinného rozvoje π jistý Rajveer Meena z Indie, který v roce 2015 dokázal odrecitovat 70 000 Ludolfových číslic! Trvalo mu to 9 hodin a 27 minut. Japonský inženýr jménem Akira Haraguchi jich sice dokázal údajně odříkat 100 000, ale tento údaj Guinnessova kniha nepotvrdila.
Pro nás normální smrtelníky, kteří nemáme tak fenomenální paměť, existují různé mnemotechnické pomůcky, jak si pár úvodních číslic zapamatovat bez trvalých následků na duševním zdraví. Nejznámější z nich jsou krátké věty, ve kterých počet písmen jednotlivých slov odpovídá začátku desetinného rozvoje pí (tam, kde je v desetinném rozvoji nula, uvažuje se obvykle slovo o deseti písmenech). Takovým textům se v angličtině říká piem, což je složenina z výrazů pi a poem (báseň).
Celkem známý piem v angličtině je například tento (3,14159265):
How I wish I could recollect pi easily today!
O něco delší je tenhle (3,141 592 653 589 79):
How I need a drink, alcoholic in nature, after the tough chapters involving quantum mechanics!
Ale i v češtině se dá piem celkem lehce vytvořit - zde na devět míst:
Sám u sebe v hlavě magického pí číslic deset mám.
A tady dokonce na 30 desetinných míst:
Mám ó bože ó velký pamatovat si takový cifer řad, velký slovutný Archimedes, pomáhej trápenému, dej mu moc, nazpaměť nechť odříká ty slavné sice, ale tak protivné nám, ach, číslice Ludolfovy.
Takový textík se samozřejmě pamatuje snadněji než tok číslovek.
Pokud si chcete vytvořit svůj vlastní piem, nebo dokonce vymyslet v podobném duchu celý román, můžete si opsat pí na milion desetinných míst.
Sekce jauvajs: Vzorečky, móc vzorečků
Protože siny a kosiny nejsou algebraické funkce, počítá se s nimi trochu jinak než třeba s polynomy. Svět goniometrických vzorečků je jedna obrovská džungle, ve které se občas ztratí i nejeden radiány ošlehaný matematik. Nebudu vás unavovat jejich podrobným výčtem (kdo si nutně potřebuje potýrat ducha, nechť popatří sem), ale abychom si z té džungle odnesli alespoň malý zážitek, vybral jsem si jeden celkem známý vzoreček pro sinus součtu dvou úhlů a podíváme se, co taková věcička dokáže (pro rozumné hodnoty úhlů).
Vzoreček nám ukazuje, jak se sinus součtu úhlů vyjádří pomocí těch původních.
sin(A+B) = sin(A) cos(B) + sin(B) cos(A)
Taková identita (rovnice) se dá ukázat mnoha způsoby. Já jsem si vybral jeden, který se navrací k původní trojúhelníkové metodice starých Řeků a je přístupný všem, kdo ovládají středoškolskou geometrii.
Začneme tím, že si zopakujeme, že obsah trojúhelníku se rovná základna krát výška děleno dvěma, přičemž je jedno, kterou stranu si vybereme za základnu. Trojúhelník samozřejmě nemusí být pravoúhlý, ale v okamžiku, kdy spustíme výšku, tam jeden pravoúhlý trojúhelník dostaneme (viz levá část následujícího obrázku) a ten nám umožní vyjádřit výšku pomocí jedné ze zbývajících stran. Takže pro obsah celého trojúhelníku dostaneme:
P = základna * výška / 2 = c * b * sin(A) / 2
a protože za základnu si můžeme vybrat libovolnou stranu, znamená to, že obsah můžeme spočítat tak, že vezmeme součin délek libovolných dvou stran, vynásobíme jej sinem úhlu těmito stranami sevřeného a na závěr vezmeme polovinu.
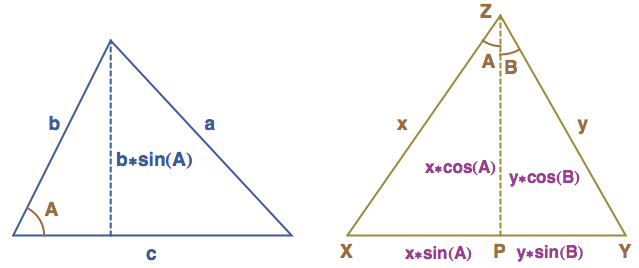
Pomocí této poučky už formulku pro součet úhlů dáme do kupy. Nejprve si
vytvoříme následující konstrukci (levá strana obrázku): na vodorovné ose
si vybereme libovolně bod P a v něm vztyčíme kolmici. Na ní si opět
libovolně zvolíme bod Z a na jedné jeho straně vyměříme úhel A a na
druhé úhel B. Přímky vedené pod těmito úhly protnou naši základnu v bodech X a Y. Délku příslušných stran v trojúhelníku XYZ si označíme
jako x a y. Tento trojúhelník nemusí být pravoúhlý, ale sestává ze dvou
menších trojúhelníků - XPZ a YPZ - které už pravoúhlé jsou, což
znamená, že délky jejich stran můžeme dopočítat pomocí goniometrických
funkcí (na obrázku uvedeny fialově).
Teď si spočítáme, jaké jsou obsahy všech tří trojúhelníků pomocí výše popsané poučky (a abych se nemusel tahat s polovinami, budu si hned zapisovat dvojnásobky obsahů P). Pro trojúhelník XYZ si vyberu strany x a y, které svírají úhel A+B. Takže, první strana krát druhá strana krát sinus sevřeného úhlu:
2 * P = x * y * sin(A+B)
Pro trojúhelník XPZ si vyberu strany svírající úhel A s tím, že pro délku kolmice použiji vyjádření pomocí y, tedy y*cos(B). Dostaneme tak následující obsah Px.
2 * Px = x * y * cos(B) * sin(A)
Pro obsah Py trojúhelníku napravo budeme postupovat zrcadlově. Takže dvě strany svírající úhel B budou y a x*cos(A), což je výška, opět vyjádřená pomocí „druhého“ trojúhelníku.
2 * Py = y * x * cos(A) * sin(B)
Závěrem si uvědomíme, že obsah velkého trojúhelníku se rovná součtu obsahů dvou menších, takže P = Px + Py a tedy:
x * y * sin(A+B) = x * y * cos(B) * sin(A) + y * x * cos(A) * sin(B)
Zkrátíme x * y a máme hotovo. A ani to nebolelo.
Článek je redakčně upravenou verzí blogového příspěvku na serveru
iDNES.cz. Publikováno s laskavým svolením autora.
Další díly a původní texty jsou dostupné na blogu Jana Řeháčka.